將有序數組轉換為二叉搜索樹
構造二叉搜索樹,一不小心就平衡了
將有序數組轉換為二叉搜索樹
力扣題目鏈接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree
將一個按照升序排列的有序數組,轉換為一棵高度平衡二叉搜索樹。
本題中,一個高度平衡二叉樹是指一個二叉樹每個節點 的左右兩個子樹的高度差的絕對值不超過 1。
示例:
思路
做這道題目之前大家可以了解一下這幾道:
- 從中序與后序遍歷序列構造二叉樹
- 最大二叉樹
- 二叉搜索樹中的插入操作
- 刪除二叉搜索樹中的節點
進入正題:
題目中說要轉換為一棵高度平衡二叉搜索樹。這和轉換為一棵普通二叉搜索樹有什么差別呢?
其實這里不用強調平衡二叉搜索樹,數組構造二叉樹,構成平衡樹是自然而然的事情,因為大家默認都是從數組中間位置取值作為節點元素,一般不會隨機取,所以想構成不平衡的二叉樹是自找麻煩。
在二叉樹:構造二叉樹登場!和二叉樹:構造一棵最大的二叉樹中其實已經講過了,如果根據數組構造一顆二叉樹。
本質就是尋找分割點,分割點作為當前節點,然后遞歸左區間和右區間。
本題其實要比二叉樹:構造二叉樹登場! 和 二叉樹:構造一棵最大的二叉樹簡單一些,因為有序數組構造二叉搜索樹,尋找分割點就比較容易了。
分割點就是數組中間位置的節點。
那么為問題來了,如果數組長度為偶數,中間節點有兩個,取哪一個?
取哪一個都可以,只不過構成了不同的平衡二叉搜索樹。
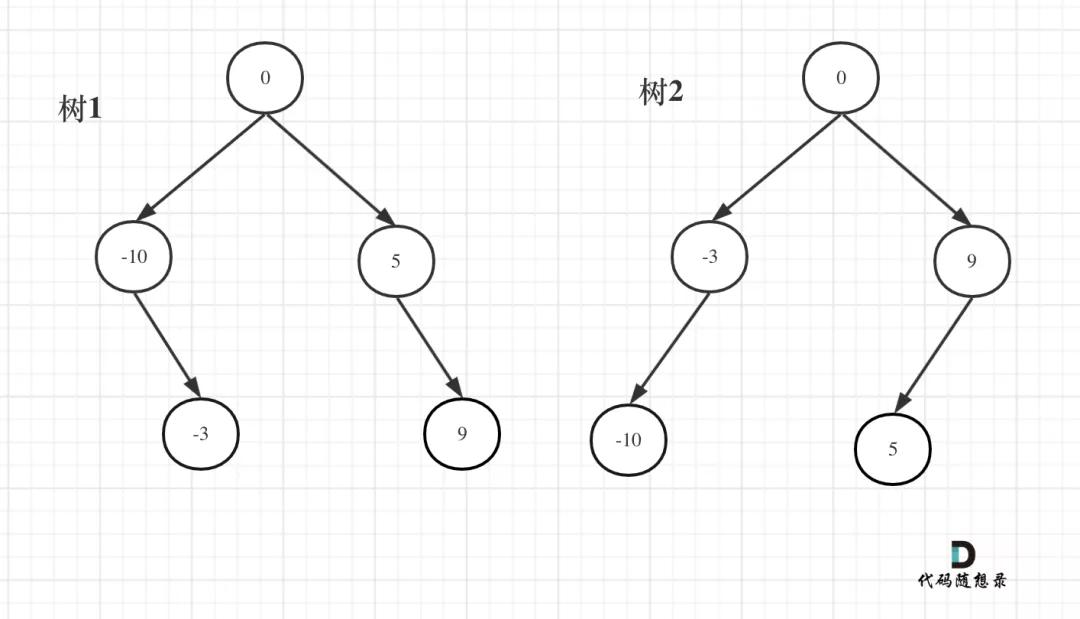
例如:輸入:[-10,-3,0,5,9]
如下兩棵樹,都是這個數組的平衡二叉搜索樹:
將有序數組轉換為二叉搜索樹
如果要分割的數組長度為偶數的時候,中間元素為兩個,是取左邊元素 就是樹1,取右邊元素就是樹2。
這也是題目中強調答案不是唯一的原因。理解這一點,這道題目算是理解到位了。
遞歸
遞歸三部曲:
- 確定遞歸函數返回值及其參數
刪除二叉樹節點,增加二叉樹節點,都是用遞歸函數的返回值來完成,這樣是比較方便的。
相信大家如果仔細看了二叉樹:搜索樹中的插入操作和二叉樹:搜索樹中的刪除操作,一定會對遞歸函數返回值的作用深有感觸。
那么本題要構造二叉樹,依然用遞歸函數的返回值來構造中節點的左右孩子。
再來看參數,首先是傳入數組,然后就是左下表left和右下表right,我們在二叉樹:構造二叉樹登場!中提過,在構造二叉樹的時候盡量不要重新定義左右區間數組,而是用下表來操作原數組。
所以代碼如下:
- // 左閉右閉區間[left, right]
- TreeNode* traversal(vector<int>& nums, int left, int right)
這里注意,我這里定義的是左閉右閉區間,在不斷分割的過程中,也會堅持左閉右閉的區間,這又涉及到我們講過的循環不變量。
數組:每次遇到二分法,都是一看就會,一寫就廢;nj 在二叉樹:構造二叉樹登場!,704. 二分查找 和59.螺旋矩陣II都詳細講過循環不變量。
- 確定遞歸終止條件
這里定義的是左閉右閉的區間,所以當區間 left > right的時候,就是空節點了。
代碼如下:
- if (left > right) return nullptr;
- 確定單層遞歸的邏輯
首先取數組中間元素的位置,不難寫出int mid = (left + right) / 2;,這么寫其實有一個問題,就是數值越界,例如left和right都是最大int,這么操作就越界了,在二分法中尤其需要注意!
所以可以這么寫:int mid = left + ((right - left) / 2);
但本題leetcode的測試數據并不會越界,所以怎么寫都可以。但需要有這個意識!
取了中間位置,就開始以中間位置的元素構造節點,代碼:TreeNode* root = new TreeNode(nums[mid]);。
接著劃分區間,root的左孩子接住下一層左區間的構造節點,右孩子接住下一層右區間構造的節點。
最后返回root節點,單層遞歸整體代碼如下:
- int mid = left + ((right - left) / 2);
- TreeNode* root = new TreeNode(nums[mid]);
- root->left = traversal(nums, left, mid - 1);
- root->right = traversal(nums, mid + 1, right);
- return root;
這里int mid = left + ((right - left) / 2);的寫法相當于是如果數組長度為偶數,中間位置有兩個元素,取靠左邊的。
- 遞歸整體代碼如下:
- class Solution {
- private:
- TreeNode* traversal(vector<int>& nums, int left, int right) {
- if (left > right) return nullptr;
- int mid = left + ((right - left) / 2);
- TreeNode* root = new TreeNode(nums[mid]);
- root->left = traversal(nums, left, mid - 1);
- root->right = traversal(nums, mid + 1, right);
- return root;
- }
- public:
- TreeNode* sortedArrayToBST(vector<int>& nums) {
- TreeNode* root = traversal(nums, 0, nums.size() - 1);
- return root;
- }
- };
注意:在調用traversal的時候為什么傳入的left和right為什么是0和nums.size() - 1,因為定義的區間為左閉右閉。
迭代法
迭代法可以通過三個隊列來模擬,一個隊列放遍歷的節點,一個隊列放左區間下表,一個隊列放右區間下表。
模擬的就是不斷分割的過程,C++代碼如下:(我已經詳細注釋)
- class Solution {
- public:
- TreeNode* sortedArrayToBST(vector<int>& nums) {
- if (nums.size() == 0) return nullptr;
- TreeNode* root = new TreeNode(0); // 初始根節點
- queue<TreeNode*> nodeQue; // 放遍歷的節點
- queue<int> leftQue; // 保存左區間下表
- queue<int> rightQue; // 保存右區間下表
- nodeQue.push(root); // 根節點入隊列
- leftQue.push(0); // 0為左區間下表初始位置
- rightQue.push(nums.size() - 1); // nums.size() - 1為右區間下表初始位置
- while (!nodeQue.empty()) {
- TreeNode* curNode = nodeQue.front();
- nodeQue.pop();
- int left = leftQue.front(); leftQue.pop();
- int right = rightQue.front(); rightQue.pop();
- int mid = left + ((right - left) / 2);
- curNode->val = nums[mid]; // 將mid對應的元素給中間節點
- if (left <= mid - 1) { // 處理左區間
- curNode->left = new TreeNode(0);
- nodeQue.push(curNode->left);
- leftQue.push(left);
- rightQue.push(mid - 1);
- }
- if (right >= mid + 1) { // 處理右區間
- curNode->right = new TreeNode(0);
- nodeQue.push(curNode->right);
- leftQue.push(mid + 1);
- rightQue.push(right);
- }
- }
- return root;
- }
- };
總結
在二叉樹:構造二叉樹登場! 和 二叉樹:構造一棵最大的二叉樹之后,我們順理成章的應該構造一下二叉搜索樹了,一不小心還是一棵平衡二叉搜索樹。
其實思路也是一樣的,不斷中間分割,然后遞歸處理左區間,右區間,也可以說是分治。
此時相信大家應該對通過遞歸函數的返回值來增刪二叉樹很熟悉了,這也是常規操作。
在定義區間的過程中我們又一次強調了循環不變量的重要性。
最后依然給出迭代的方法,其實就是模擬取中間元素,然后不斷分割去構造二叉樹的過程。
其他語言版本
Java
遞歸: 左閉右閉 [left,right]
- class Solution {
- public TreeNode sortedArrayToBST(int[] nums) {
- TreeNode root = traversal(nums, 0, nums.length - 1);
- return root;
- }
- // 左閉右閉區間[left, right)
- private TreeNode traversal(int[] nums, int left, int right) {
- if (left > right) return null;
- int mid = left + ((right - left) >> 1);
- TreeNode root = new TreeNode(nums[mid]);
- root.left = traversal(nums, left, mid - 1);
- root.right = traversal(nums, mid + 1, right);
- return root;
- }
- }
迭代: 左閉右閉 [left,right]
- class Solution {
- public TreeNode sortedArrayToBST(int[] nums) {
- if (nums.length == 0) return null;
- //根節點初始化
- TreeNode root = new TreeNode(-1);
- Queue<TreeNode> nodeQueue = new LinkedList<>();
- Queue<Integer> leftQueue = new LinkedList<>();
- Queue<Integer> rightQueue = new LinkedList<>();
- // 根節點入隊列
- nodeQueue.offer(root);
- // 0為左區間下表初始位置
- leftQueue.offer(0);
- // nums.size() - 1為右區間下表初始位置
- rightQueue.offer(nums.length - 1);
- while (!nodeQueue.isEmpty()) {
- TreeNode currNode = nodeQueue.poll();
- int left = leftQueue.poll();
- int right = rightQueue.poll();
- int mid = left + ((right - left) >> 1);
- // 將mid對應的元素給中間節點
- currNode.val = nums[mid];
- // 處理左區間
- if (left <= mid - 1) {
- currNode.left = new TreeNode(-1);
- nodeQueue.offer(currNode.left);
- leftQueue.offer(left);
- rightQueue.offer(mid - 1);
- }
- // 處理右區間
- if (right >= mid + 1) {
- currNode.right = new TreeNode(-1);
- nodeQueue.offer(currNode.right);
- leftQueue.offer(mid + 1);
- rightQueue.offer(right);
- }
- }
- return root;
- }
- }
Python
遞歸法:
- class Solution:
- def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
- def buildaTree(left,right):
- if left > right: return None #左閉右閉的區間,當區間 left > right的時候,就是空節點,當left = right的時候,不為空
- mid = left + (right - left) // 2 #保證數據不會越界
- val = nums[mid]
- root = TreeNode(val)
- root.left = buildaTree(left,mid - 1)
- root.right = buildaTree(mid + 1,right)
- return root
- root = buildaTree(0,len(nums) - 1) #左閉右閉區間
- return root
本文轉載自微信公眾號「代碼隨想錄」,可以通過以下二維碼關注。轉載本文請聯系代碼隨想錄公眾號。