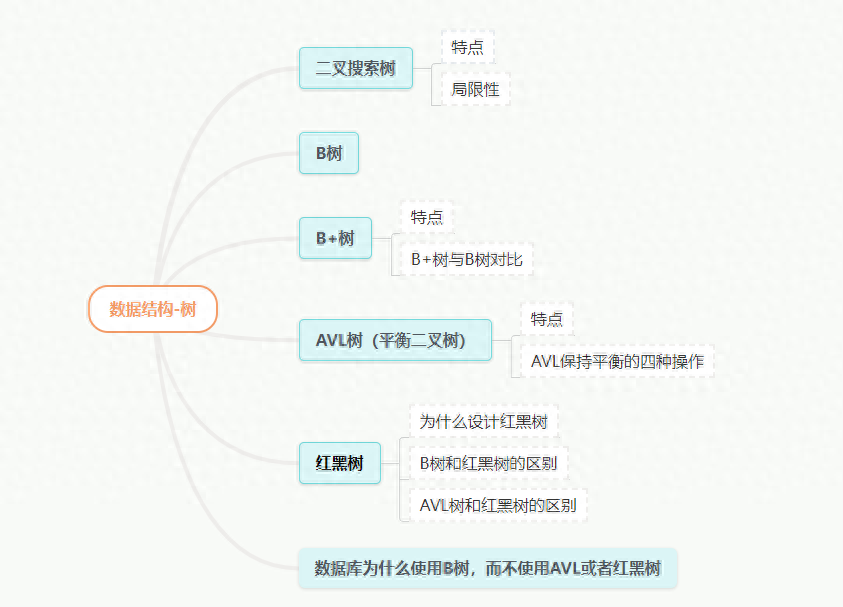
大綱

在了解 B樹、B+樹、AVL樹、紅黑樹 之前，我們先看一下各種樹型結構的大致實際應用場景：

B和B+樹：主要用在文件系統以及數據庫中做索引等AVL樹：平衡二叉樹之一，應用相對其他數據結構比較少，windows對進程地址空間的管理用到了AVL紅黑樹：平衡二叉樹，廣泛應用在C++STL中，比如map和set，Java的TreeMap

樹結構已經有了很多種形式，為何出現 B樹、B+樹、AVL樹、紅黑樹？下面我們按照這個大綱來看一下這些問題？

二叉搜索樹

概念

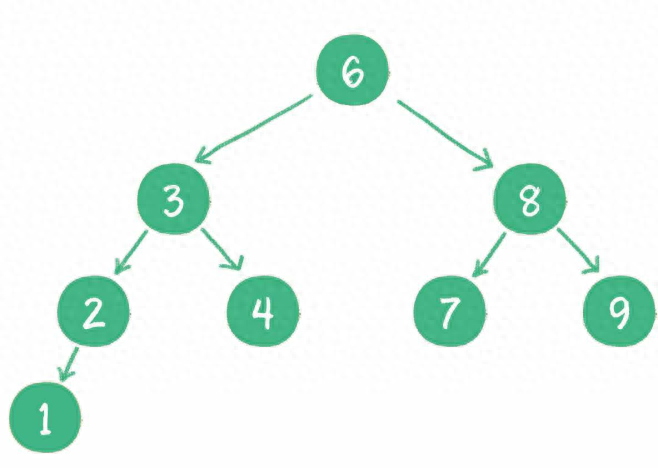
二叉搜索樹 (平衡二叉樹) 是采用二分法思維把數據按規則組裝成一個樹形結構的數據，用這個樹形結構的數據減少無關數據的檢索，大大的提升了數據檢索的速度。

我們在二叉搜索樹的深度遍歷過程中，使用中序遍歷，就能獲取得到有序的序列。

特點

• 如果任意節點左子樹不為空，則左子樹的值均小于根節點的值。
• 如果任意節點右子樹不為空，則右子樹的值均大于于根節點的值。
• 任意節點的左右子樹也分別是二叉查找樹。
• 沒有鍵值相等的節點。

存在的局限

對于一個節點分布相對均衡 的二叉查找樹來說，如果節點總數是n，那 么搜索節點的時間復雜度就是O(logn) ，和樹的深度是一樣的。 這種依靠比較大小來逐步查找的方式，和二分查找算法非常相似。

出現一些特殊的情況的時候，會導致搜索節點的時間復雜度變高。什么特殊情況呢？下面請試著在二叉查找樹中依次插入10、11、9、8、7、6、5、4，看看會出現什么 ? 好好的一個二叉樹，變成“跛腳”啦！

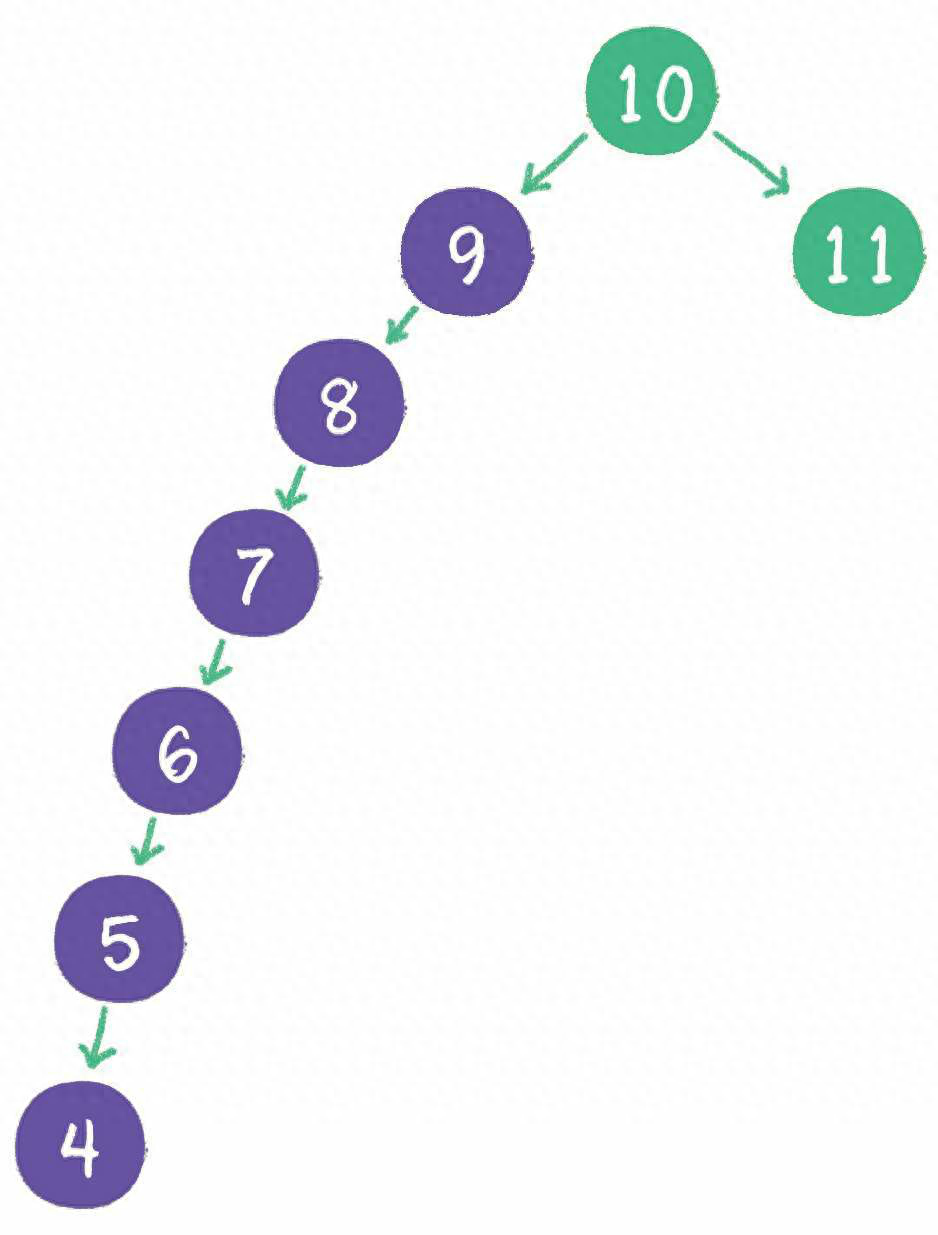
不只是外觀看起來變得怪異了，查詢節點的時間復雜度也退化成了O(n)。 怎么解決這個問題呢？這就涉及二叉樹的自平衡 了。二叉樹自平衡的方式有多種，如紅黑樹、AVL樹等，這兩種我們在后面會介紹到，我們先來看一下B樹和B+樹。

B樹

概念

B樹又名平衡多路查找樹（也把B樹稱為B-樹）查找路徑不只兩個，不同于常見的二叉樹，它是一種多叉樹，我們常見的使用場景一般是在數據庫索引技術里，大量使用者B樹和B+樹的數據結構。

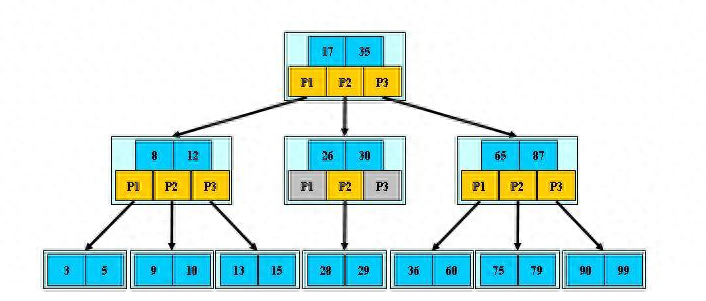
B樹大多用在磁盤上用于查找磁盤的地址。因為磁盤會有大量的數據，有可能沒有辦法一次將需要的所有數據加入到內存中，所以只能逐一加載磁盤頁，每個磁盤頁就對應一個節點，而對于B樹來說，B樹很好的將樹的高度降低了，這樣就會減少IO查詢次數，雖然一次加載到內存的數據變多了，但速度絕對快于AVL或是紅黑樹的。

特點：

• 所有鍵值分布在整個樹中（區別與B+樹，B+樹的值只分部在葉子節點上）
• 任何關鍵字出現且只出現在一個節點中（區別與B+樹）
• 搜索有可能在非葉子節點結束（區別與B+樹，因為值都在葉子節點上，只有搜到葉子節點才能拿到值）
• 在關鍵字全集內做一次查找，性能逼近二分查找算法

查詢分析

• 如果要查找數據項29，那么首先會把磁盤塊1由磁盤加載到內存，此時發生一次IO，在內存中用二分查找確定29在17和35之間，鎖定磁盤塊1的P2指針，內存時間因為非常短（相比磁盤的IO）可以忽略不計，
• 通過磁盤塊1的P2指針的磁盤地址把磁盤塊3由磁盤加載到內存，發生第二次IO，29在26和30之間，鎖定磁盤塊3的P2指針，
• 通過指針加載磁盤塊8到內存，發生第三次IO，同時內存中做二分查找找到29，結束查詢，總計三次IO。

B+樹

概念

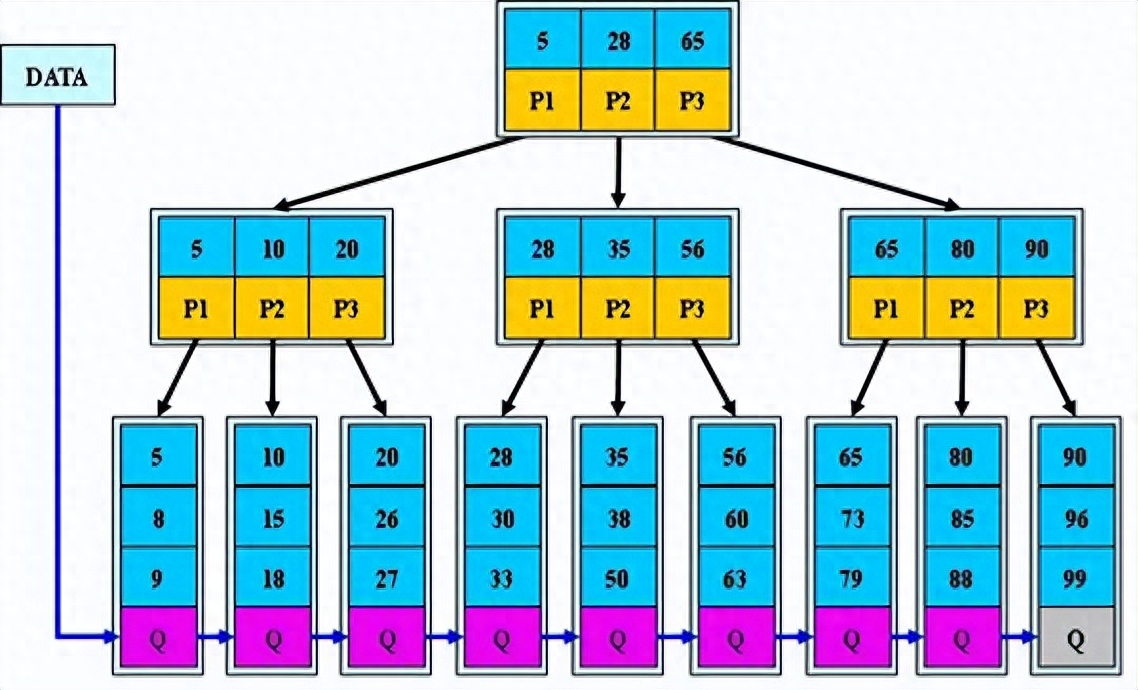
特點

• 所有葉子節點連接成為一個單鏈表，且這個鏈表是有序的。
• 所有關鍵字都在葉子節點出現，因此不可能在非葉子節點命中。
• 內節點不存數據，只存key。
• 非葉子節點相當于是葉子節點的索引，葉子節點相當于是存儲數據的數據層。

B+Tree與B-Tree 的區別

1）B樹的關鍵字和記錄是放在一起的，葉子節點可以看作外部節點，不包含任何信息；B+樹的非葉子節點中只有關鍵字和指向下一個節點的索引，記錄只放在葉子節點中。

2）在B樹中，越靠近根節點的記錄查找時間越快，只要找到關鍵字即可確定記錄的存在；而B+樹中每個記錄的查找時間基本是一樣的，都需要從根節點走到葉子節點，而且在葉子節點中還要再比較關鍵字。

思考：為什么說B+tree比B-tree更適合實際應用中操作系統的文件索引和數據庫索引？

1) B+樹的磁盤讀寫代價更低

　　B+樹的內部結點并沒有指向關鍵字具體信息的指針。因此其內部結點相對B 樹更小。如果把所有同一內部結點的關鍵字存放在同一盤塊中，那么盤塊所能容納的關鍵字數量也越多。一次性讀入內存中的需要查找的關鍵字也就越多。相對來說IO讀寫次數也就降低了。

2) B+樹的查詢效率更加穩定

　　由于非終結點并不是最終指向文件內容的結點，而只是葉子結點中關鍵字的索引。所以任何關鍵字的查找必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同，導致每一個數據的查詢效率相當。

3)范圍查找更快

mysql是關系型數據庫，經常會按照區間來訪問某個索引列，B+樹的葉子節點間按順序建立了鏈指針，加強了區間訪問性，所以B+樹對索引列上的區間范圍查詢很友好。而B樹的數據有一部分存在在非葉子節點上面，而且默認的B樹的相鄰的葉子節點之間是沒有指針的，所以范圍查找相對更慢。

AVL樹（平衡二叉樹）

概念

AVL、紅黑樹是對二叉搜索樹的改進版本。

平衡因子：某個節點的左右子樹深度之差。在一棵平衡二叉樹中，節點的平衡因子只能取 0 、1 或者 -1 ，分別對應著左右子樹等高，左子樹比較高，右子樹比較高。

AVL樹是帶有平衡條件的二叉查找樹，一般是用平衡因子差值判斷是否平衡并通過旋轉來實現平衡，左右子樹樹高不超過1，和紅黑樹相比，它是嚴格的平衡二叉樹，平衡條件必須滿足（所有節點的左右子樹高度差不超過1）。

不管我們是執行插入還是刪除操作，只要不滿足上面的條件，就要通過旋轉來保持平衡，而旋轉是非常耗時的，由此我們可以知道AVL樹適合用于插入刪除次數比較少，但查找多的情況。

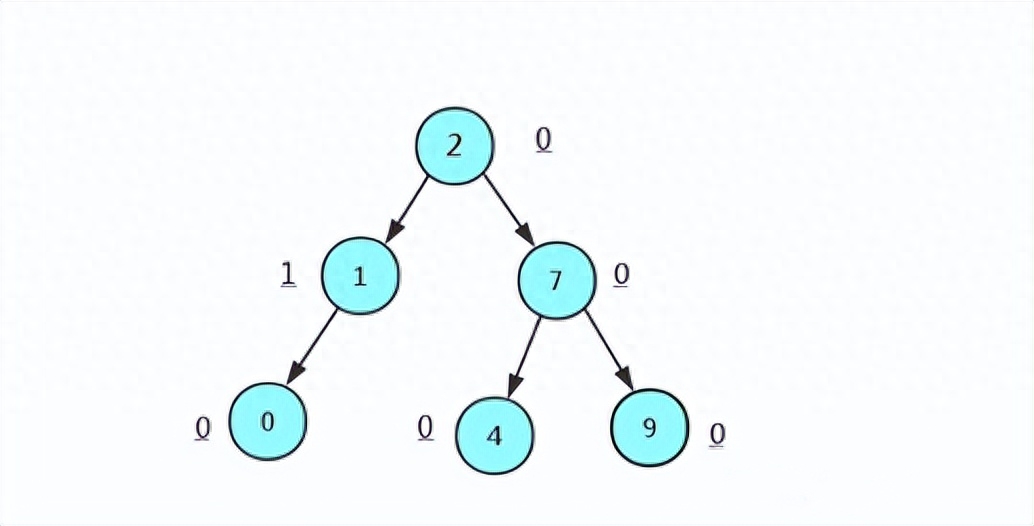
如上圖所示：任意節點的左右子樹的平衡因子差值都不會大于1

AVL保持平衡的四種操作

增刪改查操作和二分搜索樹類似，但是要多考慮的就是對節點的平衡考慮，如果一串數字的插入順序為3，4，5。那么這棵樹結構就會退化為一個鏈表。而這時候AVL就會對這個樹進行旋轉操作來達到平衡，所以，我們就知道旋轉的操作會在增加，刪除，修改這三個地方進行旋轉。旋轉操作分為下面四種情況

1 LL右單旋轉

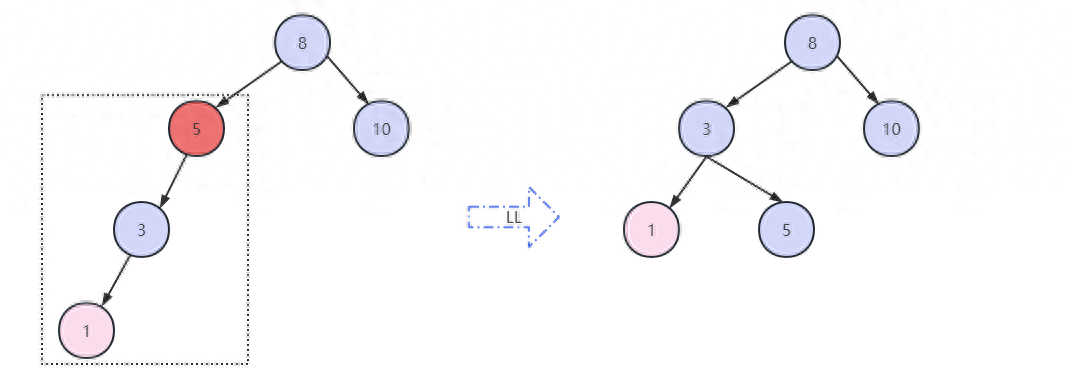
如圖，8的左子樹已經退化為鏈表，并且5，8這兩個節點不再平衡，這時我們先找到深度最深的不平衡節點5，對節點5進行LL旋轉操作，在如圖的這種情況下，得到右圖的結構

2 RR左單旋轉

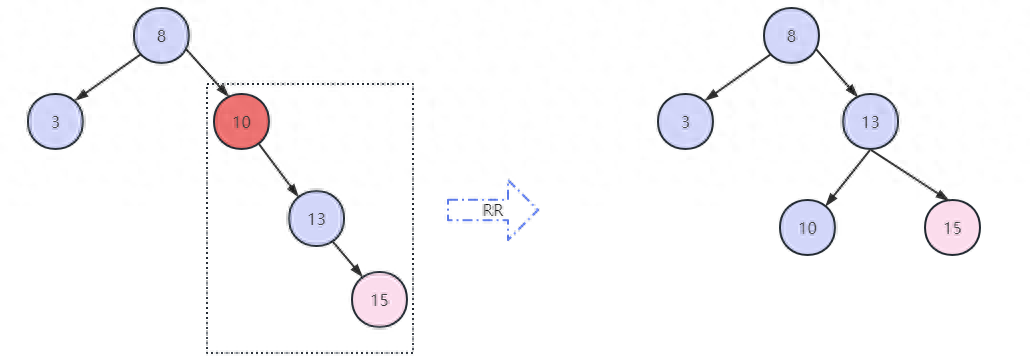
如圖，當插入順序為當插入順序為8，3，10，13，15的時候，樹的結構變成左邊的樣子，這時10節點和8節點已經不平衡，為了保持AVL的平衡，我們要對10節點進行RR旋轉，如右圖所示

3 LR先左后右

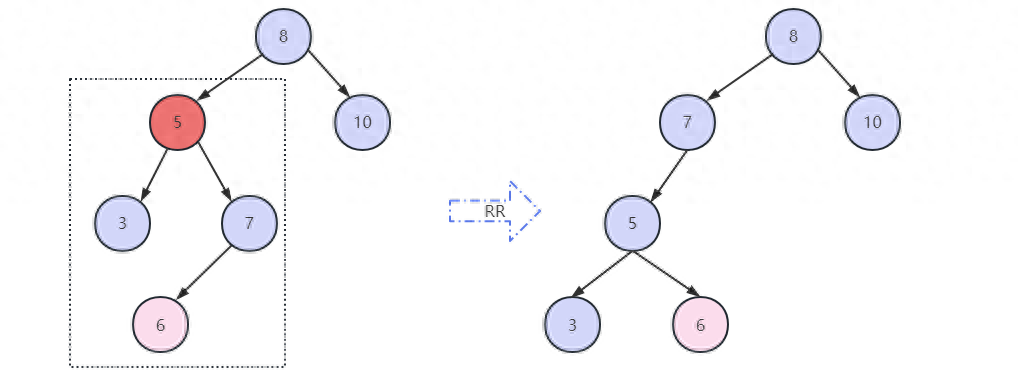
如圖。5，8節點已經不平衡，這時要對5節點做平衡處理，首先將5進行RR左旋轉，7的左節點也變為5的右節點。

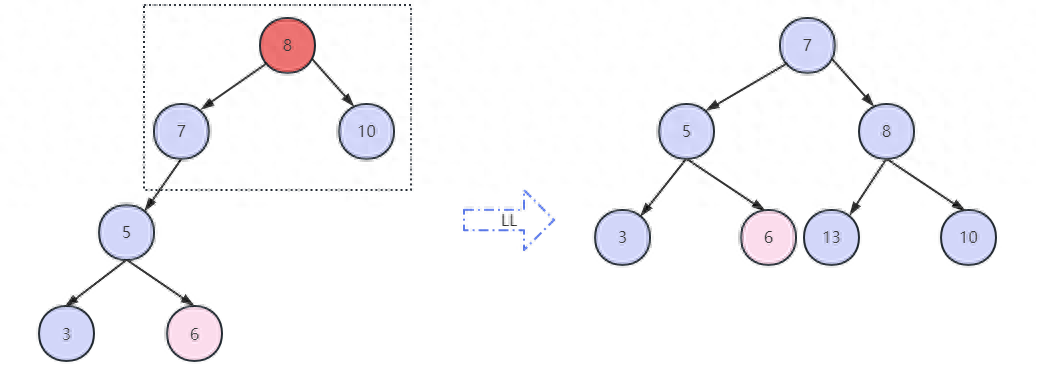
這時7，8還是不平衡的，對8進行右旋轉，8的右節點也變為8的左節點，如圖。

4 RL先右后左

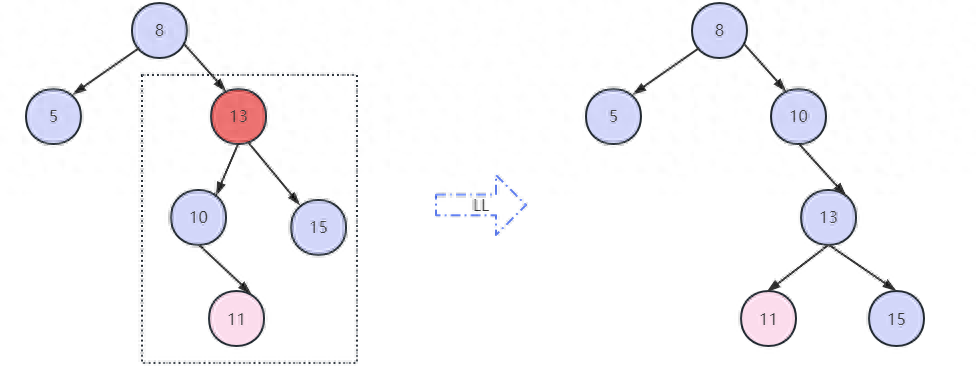
如左圖，8，13節點不平衡，對13節點進行LL右旋轉，得到右圖

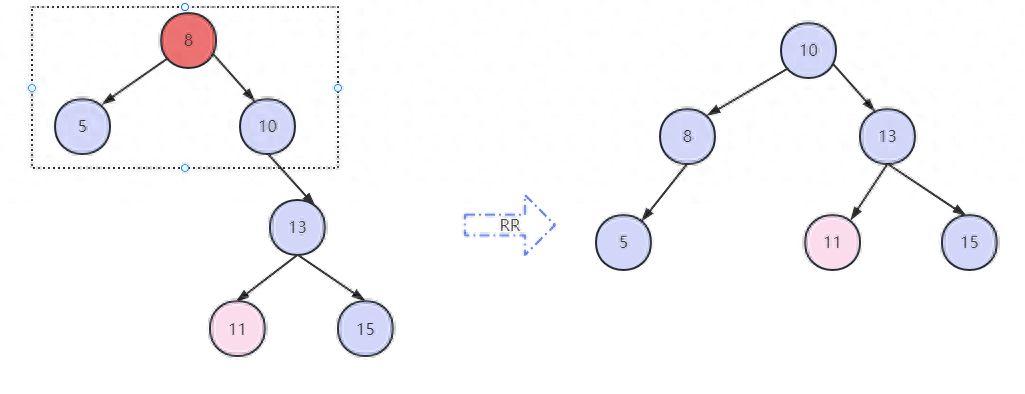
這時8，10是不平衡的，對8節點進行RR左旋轉，得到右圖。

紅黑樹

概念

一種二叉查找樹，但在每個節點增加一個存儲位表示節點的顏色，可以是red或black（非紅即黑）。通過對任何一條從根到葉子的路徑上各個節點著色的方式的限制，紅黑樹確保沒有一條路徑會比其它路徑長出兩倍。它是一種弱平衡二叉樹，相對于要求嚴格的AVL樹來說，它的旋轉次數少，所以對于插入、刪除操作較多的情況下，我們就用紅黑樹。

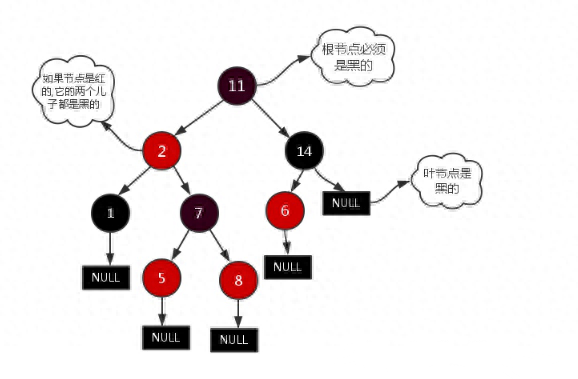
特點

• 每個節點非紅即黑；
• 根節點是黑的；
• 每個葉節點(葉節點即樹尾端NULL指針或NULL節點)都是黑的；
• 如果一個節點是紅的,那么它的兩兒子都是黑的；
• 對于任意節點而言，其到葉子點樹NULL指針的每條路徑都包含相同數目的黑節點；
• 高度始終保持在h = logn
• 一般插入的是紅色結點

紅黑樹的自平衡操作

紅黑樹插入

兩個操作：旋轉+變色

在紅黑樹的結點上添加20，剛開始作為50的左子結點，這樣不符合紅黑樹的規則，并且這樣的情況滿足上面說的情況5，因此50結點會變成黑色，根結點右旋。先完成右旋，再完成變色。

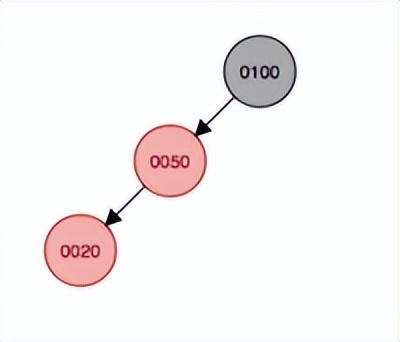旋轉

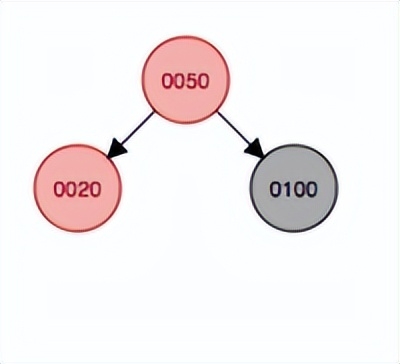變色

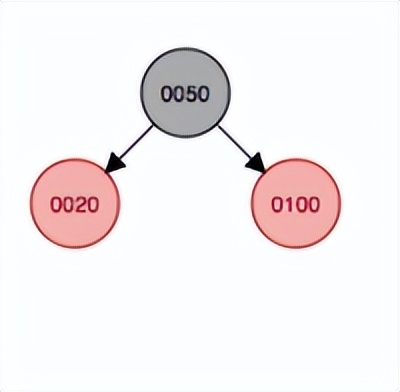
繼續添加結點200，首先會作為100的右結點添加，因此父結點和叔叔結點都變成黑色，祖父結點50變成紅色，然后根節點不能為紅色，因此繼續變色，最后根節點變成黑色。需要注意的是紅色節點的子結點必須為黑色節點，但是沒有規定黑色節點的子結點必須為紅色，說明黑色節點下面子結點什么顏色都可以。

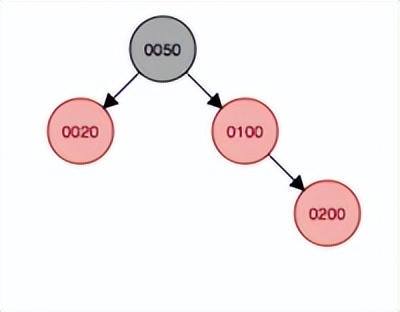變色

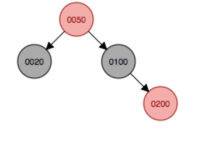繼續變色

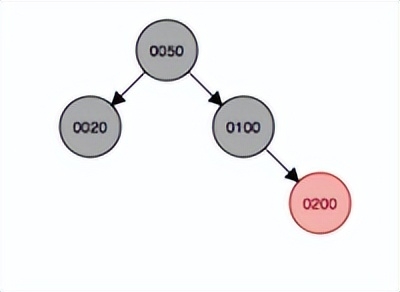
繼續添加結點300，首先會作為子結點添加到200的右子結點，因此首先以插入結點的祖父結點100為支點發生左旋，然后變色，父結點200變成黑色，原祖父結點變成紅色。

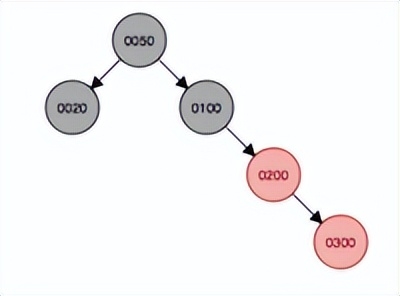左旋

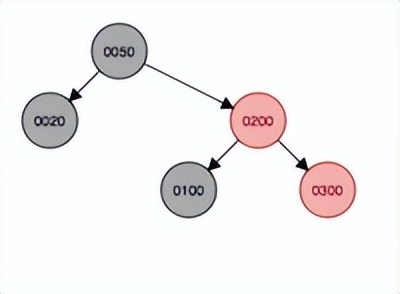變色

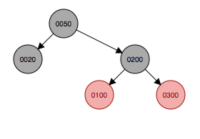
繼續添加結點150，首先會作為子結點添加到100的右子結點，因此父結點和叔叔結點變成黑色，祖父結點200變成紅色，變完色后發現符合黑紅樹規則，無需再旋轉或變色。

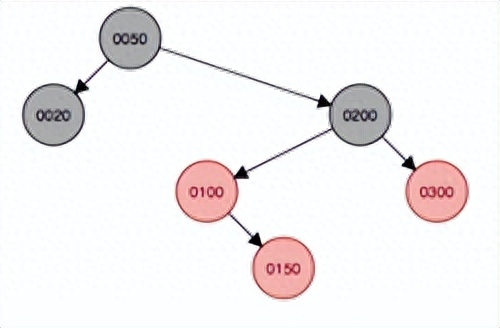變色

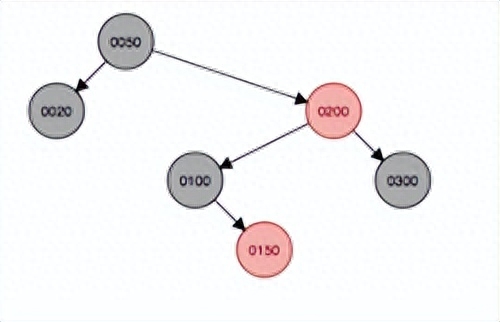
繼續添加元素160，會先作為右結點掛在150下面，然后這種情況符合上面第五種，因此先按照祖父結點100為支點左旋，然后父結點變成黑色，原祖父結點變成紅色，完后發現符合黑紅樹規則，無需再選擇或變色。

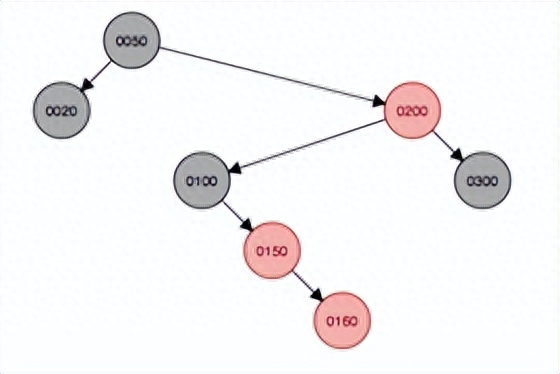左旋

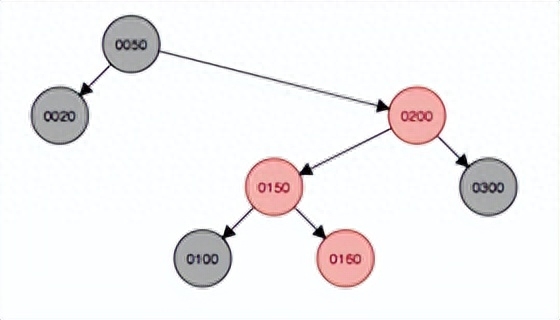變色

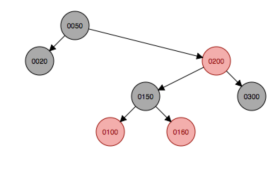
添加320到子結點，會首先掛在350下面，父結點是紅色，叔叔結點（null）為黑色，由于當前結點在父結點的左邊，因此先以父結點350為支點右旋，右旋后變成上面的第五種情況，因此先以祖父結點300左旋，然后父結點320變色為黑色，原祖父結點300變色為紅色。

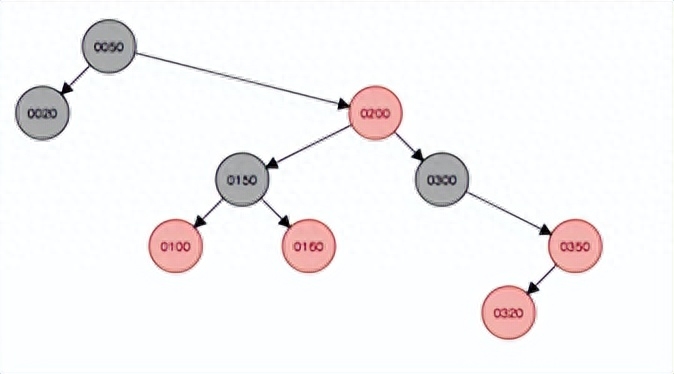右旋

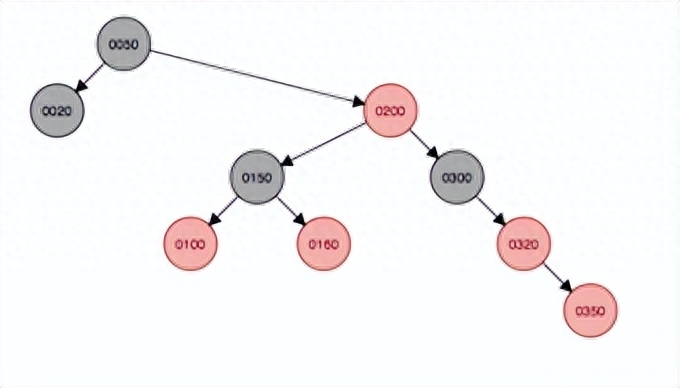左旋變色

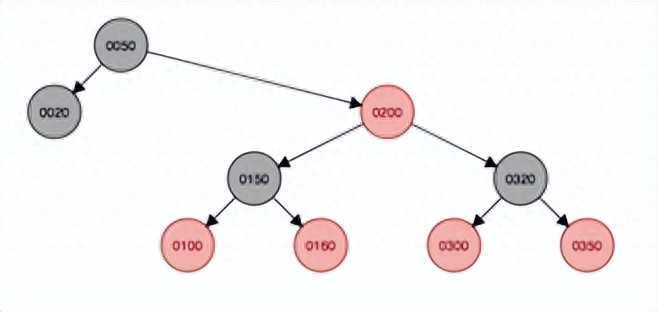
最后添加180到結點中，首先添加到160的右子結點，父結點和叔叔結點都變色為黑色，祖父結點150變成紅色。

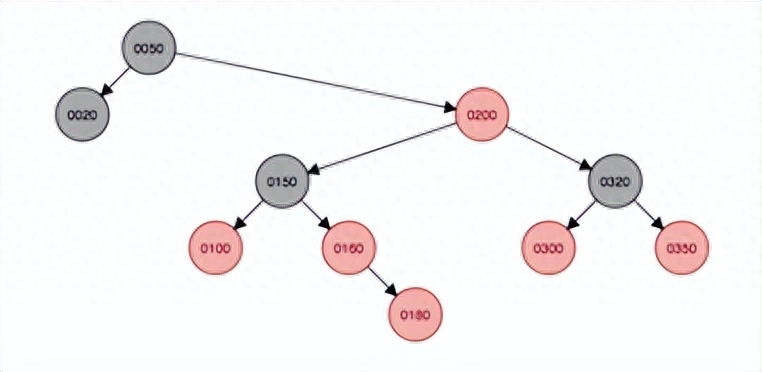變色

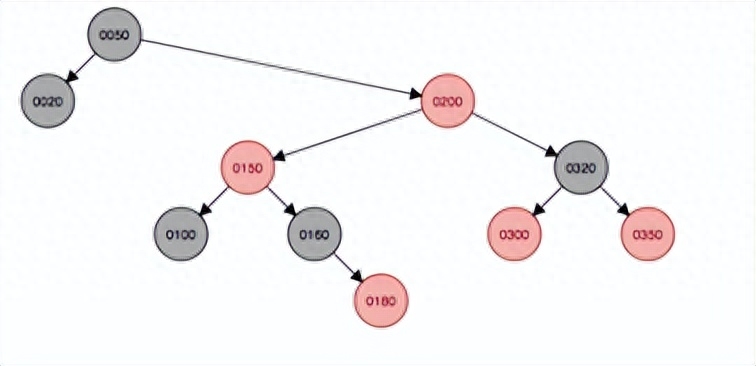
右旋變成紅色后，這種為第四種情況，即150結點的父結點是紅色，叔叔結點是黑色，因此本例中需要右旋，由于右旋后200和160會碰撞，因此160結點的子樹將作為200結點的左子樹。

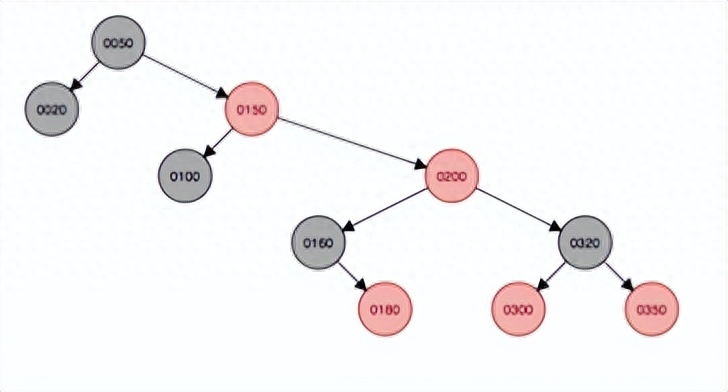
左旋需要以200結點的祖父結點50為支點左旋，由于左旋后，50和100會發生碰撞，因此100將掛在50結點的右邊。并且父結點150變成黑色，祖父結點50會變成紅色。

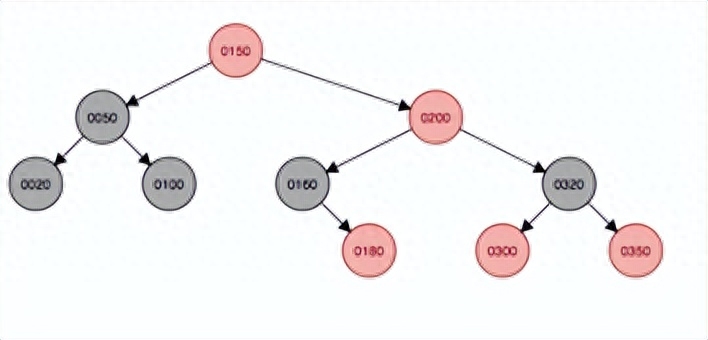變色

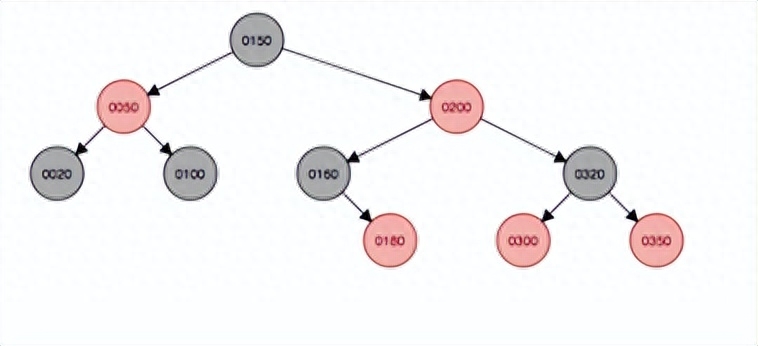
紅黑樹插入自平衡總結

• N為根：涂黑完事；
• 父黑：啥事不用管；
• 父紅叔紅：父/叔涂黑，祖父涂紅，然后把祖父當成新的平衡節點遞歸處理（我們下面平衡了，讓他老人家和上面溝通吧）；
• 父紅叔黑：父節點和新插入節點同一邊的話，扭一下就完事了（同左右旋，同右左旋，順便涂色）；不在同一邊的話，先扭到同一邊吧。

紅黑樹的刪除

紅黑樹的刪除情況相對插入會復雜一些，這這里先不過多的介紹了，肝不動了。如果感興趣的話，我們在來一起探討~~

二叉搜索樹、B樹、B+樹、AVL樹、紅黑樹的常見面試題

1 為什么設計紅黑樹

紅黑樹通過它規則的設定，確保了插入和刪除的最壞的時間復雜度是O(log N) 。

紅黑樹解決了AVL平衡二叉樹的維護起來比較麻煩的問題，紅黑樹，讀取略遜于AVL，維護強于AVL，每次插入和刪除的平均旋轉次數應該是遠小于平衡樹。

因此：相對于要求嚴格的AVL樹來說，紅黑樹的旋轉次數少，所以對于插入、刪除操作較多的情況下，我們就用紅黑樹。但是，只是對查找要求較高,那么AVL還是較優于紅黑樹.

2 B樹、B+樹和紅黑樹的區別

• 最大的區別就是樹的深度較高，在磁盤I/O方面的表現不如B樹。
• 在大規模數據存儲的時候，紅黑樹往往出現由于樹的深度過大而造成磁盤IO讀寫過于頻繁，進而導致效率低下。在這方面，B樹表現相對優異，B樹可以有多個子女，從幾十到上千，可以降低樹的高度。
• 紅黑樹多用在內部排序，即全放在內存中的，STL的map和set的內部實現就是紅黑樹。
• B+樹多用于外存上時，B+也被成為一個磁盤友好的數據結構。

3 AVL樹和紅黑樹的區別

紅黑樹的算法時間復雜度和AVL相同，但統計性能比AVL樹更高。

紅黑樹和AVL樹都能夠以O(log2 n)的時間復雜度進行搜索、插入、刪除操作。 2、由于設計，紅黑樹的任何不平衡都會在三次旋轉之內解決。AVL樹增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。

在查找方面： 紅黑樹的性質(最長路徑長度不超過最短路徑長度的2倍)，其查找代價基本維持在O(logN)左右，但在最差情況下(最長路徑是最短路徑的2倍少1)，比AVL要略遜色一點。 AVL是嚴格平衡的二叉查找樹（平衡因子不超過1）。查找過程中不會出現最差情況的單支樹。因此查找效率最好，最壞情況都是O(logN)數量級的。

所以，綜上： AVL比RBtree更加平衡，但是AVL的插入和刪除會帶來大量的旋轉。 所以如果插入和刪除比較多的情況，應該使用RBtree, 如果查詢操作比較多，應該使用AVL。

4 數據庫為什么使用B樹，而不使用AVL或者紅黑樹

我們假設B+樹一個節點可以有100個關鍵字，那么3層的B樹可以容納大概1000000多個關鍵字（100+101100+101101*100）。而紅黑樹要存儲這么多至少要20層。所以使用B樹相對于紅黑樹和AVL可以減少IO操作

5 為什么B+樹比B樹更為友好

• 磁盤讀寫代價更低 樹的非葉子結點里面沒有數據，這樣索引比較小，可以放在一個blcok（或者盡可能少的blcok）里面。避免了樹形結構不斷的向下查找，然后磁盤不停的尋道，讀數據。這樣的設計，可以降低io的次數。
• 查詢效率更加穩定 非終結點并不是最終指向文件內容的結點，而只是葉子結點中關鍵字的索引。所以任何關鍵字的查找必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同，導致每一個數據的查詢效率相當。
• 遍歷所有的數據更方便 B+樹只要遍歷葉子節點就可以實現整棵樹的遍歷，而其他的樹形結構 要中序遍歷才可以訪問所有的數據。