面試官:說說你對堆的理解?如何實現?應用場景?
本文轉載自微信公眾號「JS每日一題」,作者灰灰。轉載本文請聯系JS每日一題公眾號。
一、是什么
堆(Heap)是計算機科學中一類特殊的數據結構的統稱
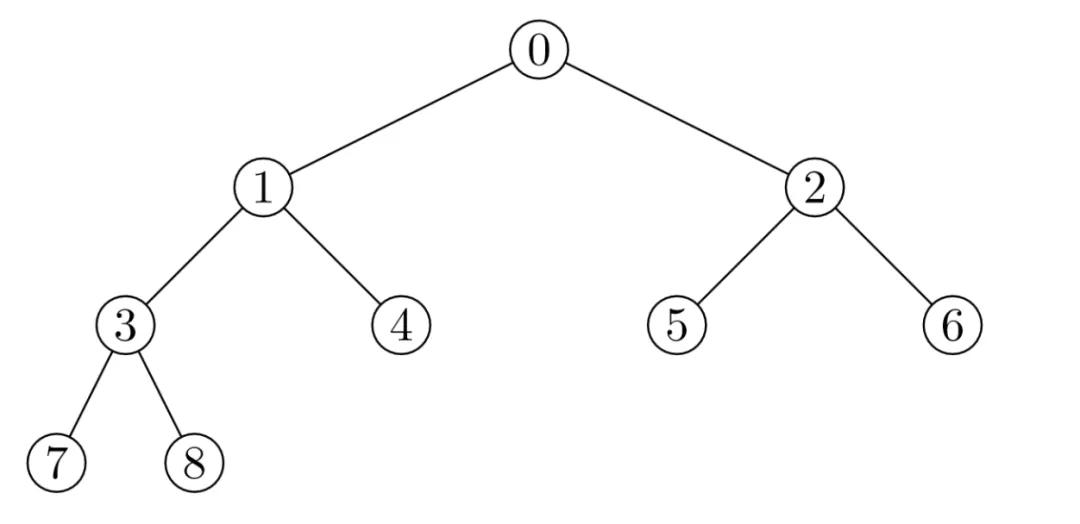
堆通常是一個可以被看做一棵完全二叉樹的數組對象,如下圖:
總是滿足下列性質:
- 堆中某個結點的值總是不大于或不小于其父結點的值
- 堆總是一棵完全二叉樹
堆又可以分成最大堆和最小堆:
- 最大堆:每個根結點,都有根結點的值大于兩個孩子結點的值
- 最小堆:每個根結點,都有根結點的值小于孩子結點的值
二、操作
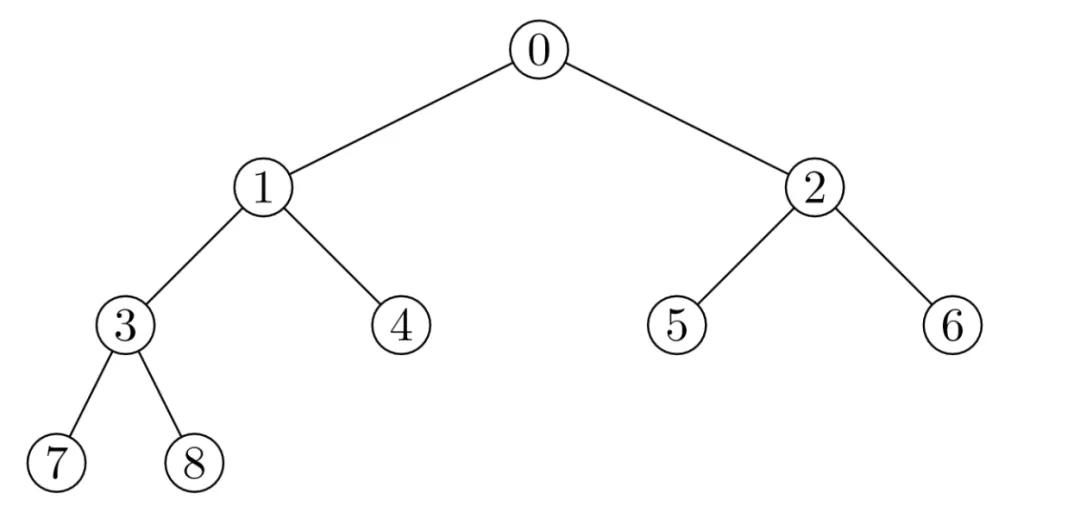
堆的元素存儲方式,按照完全二叉樹的順序存儲方式存儲在一個一維數組中,如下圖:
用一維數組存儲則如下:
- [0, 1, 2, 3, 4, 5, 6, 7, 8]
根據完全二叉樹的特性,可以得到如下特性:
- 數組零坐標代碼的是堆頂元素
- 一個節點的父親節點的坐標等于其坐標除以2整數部分
- 一個節點的左節點等于其本身節點坐標 * 2 + 1
- 一個節點的右節點等于其本身節點坐標 * 2 + 2
根據上述堆的特性,下面構建最小堆的構造函數和對應的屬性方法:
- class MinHeap {
- constructor() {
- // 存儲堆元素
- this.heap = []
- }
- // 獲取父元素坐標
- getParentIndex(i) {
- return (i - 1) >> 1
- }
- // 獲取左節點元素坐標
- getLeftIndex(i) {
- return i * 2 + 1
- }
- // 獲取右節點元素坐標
- getRightIndex(i) {
- return i * 2 + 2
- }
- // 交換元素
- swap(i1, i2) {
- const temp = this.heap[i1]
- this.heap[i1] = this.heap[i2]
- this.heap[i2] = temp
- }
- // 查看堆頂元素
- peek() {
- return this.heap[0]
- }
- // 獲取堆元素的大小
- size() {
- return this.heap.length
- }
- }
涉及到堆的操作有:
- 插入
- 刪除
插入
將值插入堆的底部,即數組的尾部,當插入一個新的元素之后,堆的結構就會被破壞,因此需要堆中一個元素做上移操作
將這個值和它父節點進行交換,直到父節點小于等于這個插入的值,大小為k的堆中插入元素的時間復雜度為O(logk)
如下圖所示,22節點是新插入的元素,然后進行上移操作:
相關代碼如下:
- // 插入元素
- insert(value) {
- this.heap.push(value)
- this.shifUp(this.heap.length - 1)
- }
- // 上移操作
- shiftUp(index) {
- if (index === 0) { return }
- const parentIndex = this.getParentIndex(index)
- if(this.heap[parentIndex] > this.heap[index]){
- this.swap(parentIndex, index)
- this.shiftUp(parentIndex)
- }
- }
刪除
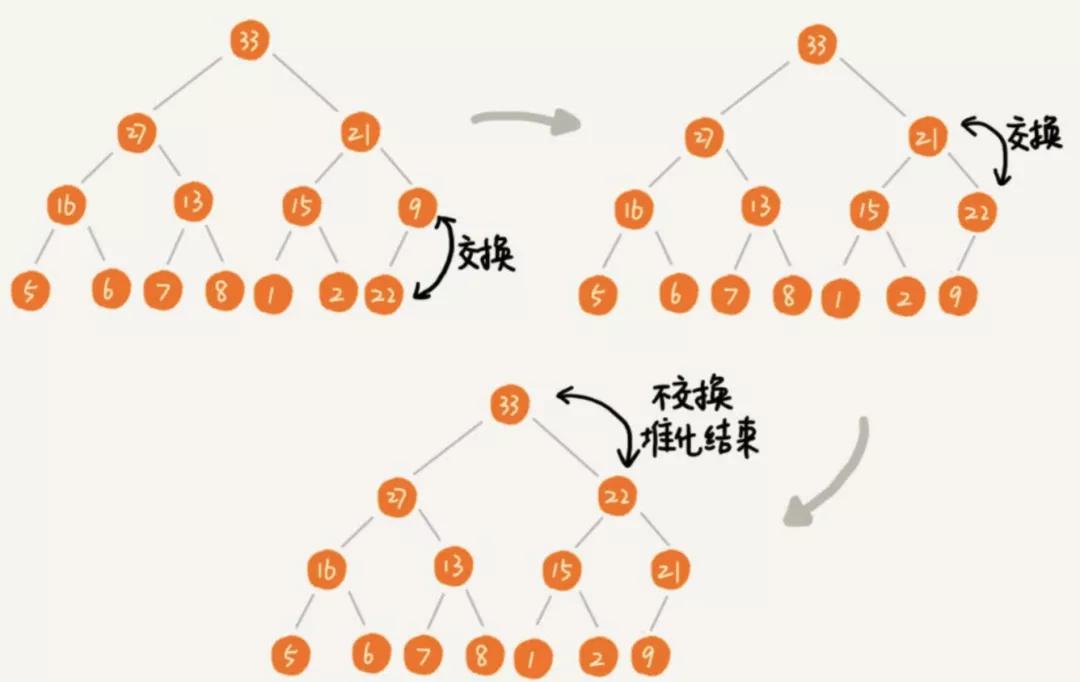
常見操作是用數組尾部元素替換堆頂,這里不直接刪除堆頂,因為所有的元素會向前移動一位,會破壞了堆的結構
然后進行下移操作,將新的堆頂和它的子節點進行交換,直到子節點大于等于這個新的堆頂,刪除堆頂的時間復雜度為O(logk)
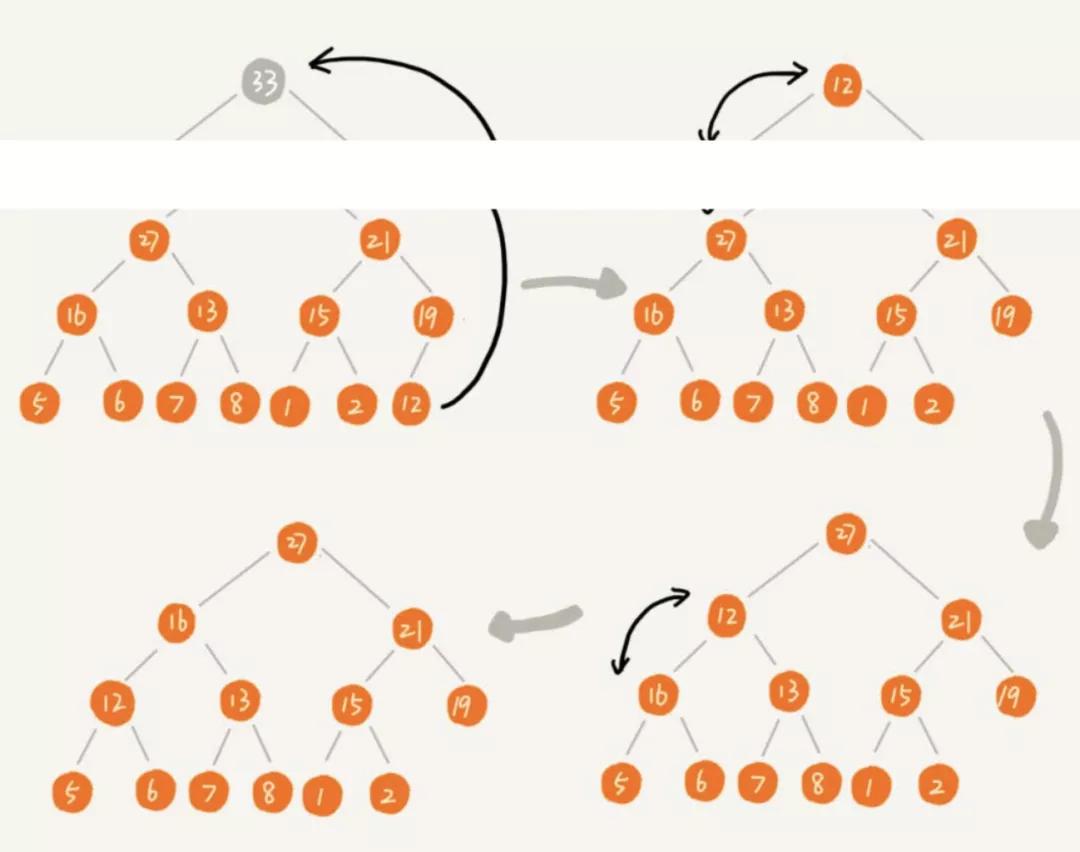
整體如下圖操作:
相關代碼如下:
- // 刪除元素
- pop() {
- this.heap[0] = this.heap.pop()
- this.shiftDown(0)
- }
- // 下移操作
- shiftDown(index) {
- const leftIndex = this.getLeftIndex(index)
- const rightIndex = this.getRightIndex(index)
- if (this.heap[leftIndex] < this.heap[index]){
- this.swap(leftIndex, index)
- this.shiftDown(leftIndex)
- }
- if (this.heap[rightIndex] < this.heap[index]){
- this.swap(rightIndex, index)
- this.shiftDown(rightIndex)
- }
- }
時間復雜度
關于堆的插入和刪除時間復雜度都是Olog(n),原因在于包含n個節點的完全二叉樹,樹的高度不會超過log2n
堆化的過程是順著節點所在路徑比較交換的,所以堆化的時間復雜度跟樹的高度成正比,也就是Olog(n),插入數據和刪除堆頂元素的主要邏輯就是堆化
三、總結
堆是一個完全二叉樹
堆中每一個節點的值都必須大于等于(或小于等于)其子樹中每個節點的值
對于每個節點的值都大于等于子樹中每個節點值的堆,叫作“大頂堆”
對于每個節點的值都小于等于子樹中每個節點值的堆,叫作“小頂堆”
根據堆的特性,我們可以使用堆來進行排序操作,也可以使用其來求第幾大或者第幾小的值
參考文獻
https://baike.baidu.com/item/%E5%A0%86/20606834
https://xlbpowder.cn/2021/02/26/%E5%A0%86%E5%92%8C%E5%A0%86%E6%8E%92%E5%BA%8F/