子集問題其實就是模板題!你知道嗎?
認識本質之后,這就是一道模板題
子集
力扣題目鏈接:https://leetcode-cn.com/problems/subsets/
給定一組不含重復元素的整數數組 nums,返回該數組所有可能的子集(冪集)。
說明:解集不能包含重復的子集。
示例:
輸入: nums = [1,2,3]
輸出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
思路
求子集問題和77.組合和131.分割回文串又不一樣了。
如果把 子集問題、組合問題、分割問題都抽象為一棵樹的話,那么組合問題和分割問題都是收集樹的葉子節點,而子集問題是找樹的所有節點!
其實子集也是一種組合問題,因為它的集合是無序的,子集{1,2} 和 子集{2,1}是一樣的。
那么既然是無序,取過的元素不會重復取,寫回溯算法的時候,for就要從startIndex開始,而不是從0開始!
有同學問了,什么時候for可以從0開始呢?
求排列問題的時候,就要從0開始,因為集合是有序的,{1, 2} 和{2, 1}是兩個集合,排列問題我們后續的文章就會講到的。
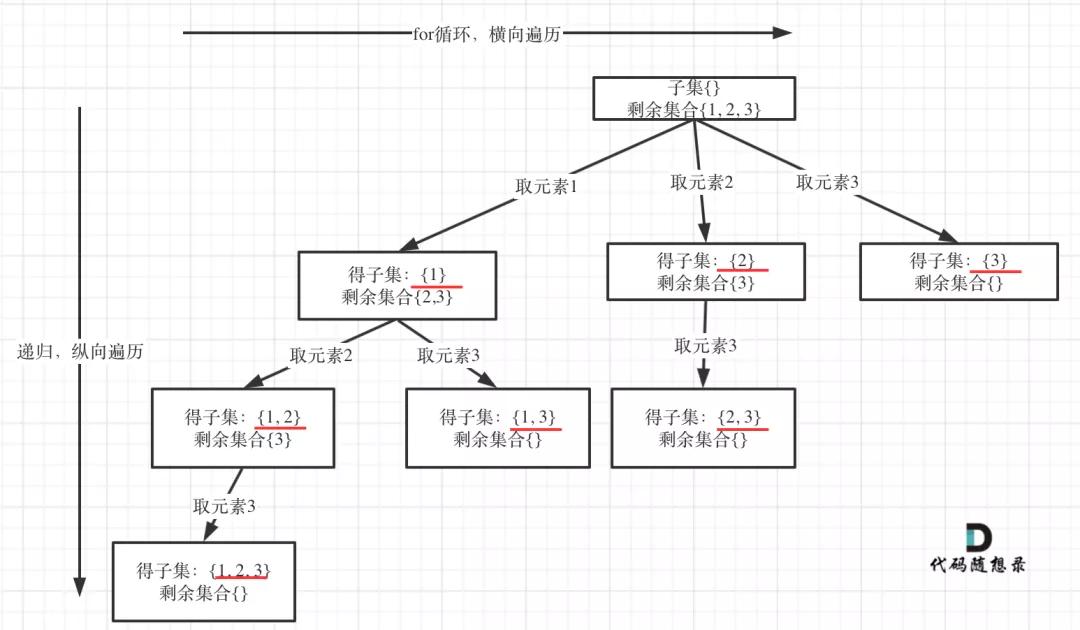
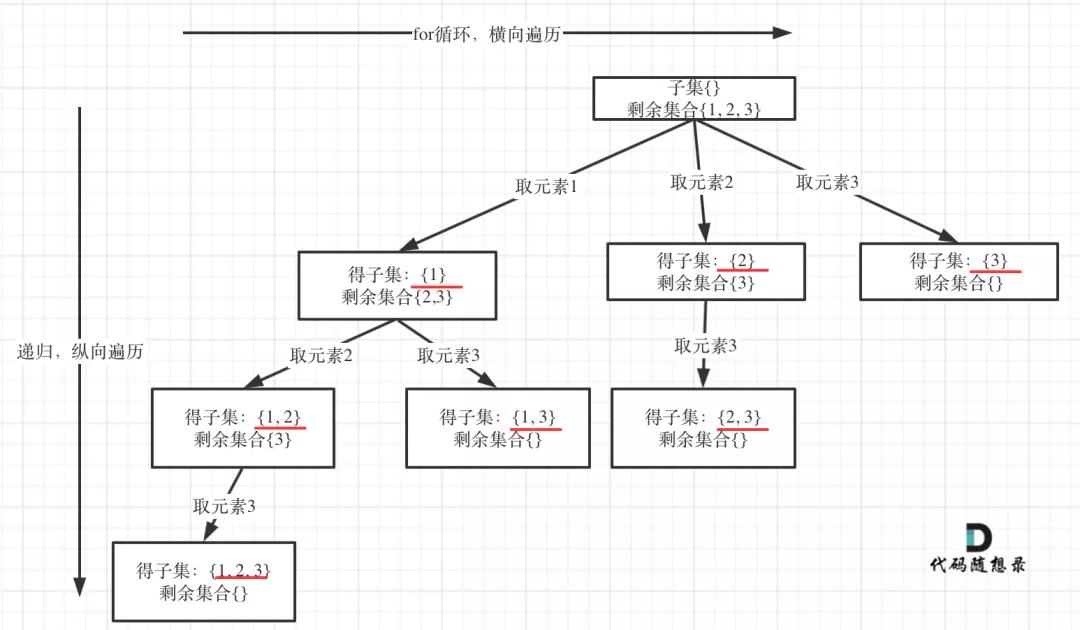
以示例中nums = [1,2,3]為例把求子集抽象為樹型結構,如下:
子集
從圖中紅線部分,可以看出遍歷這個樹的時候,把所有節點都記錄下來,就是要求的子集集合。
回溯三部曲
- 遞歸函數參數
全局變量數組path為子集收集元素,二維數組result存放子集組合。(也可以放到遞歸函數參數里)
遞歸函數參數在上面講到了,需要startIndex。
代碼如下:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
遞歸終止條件
從圖中可以看出:
子集
剩余集合為空的時候,就是葉子節點。
那么什么時候剩余集合為空呢?
就是startIndex已經大于數組的長度了,就終止了,因為沒有元素可取了,代碼如下:
- if (startIndex >= nums.size()) {
- return;
- }
其實可以不需要加終止條件,因為startIndex >= nums.size(),本層for循環本來也結束了。
- 單層搜索邏輯
求取子集問題,不需要任何剪枝!因為子集就是要遍歷整棵樹。
那么單層遞歸邏輯代碼如下:
- for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]); // 子集收集元素
- backtracking(nums, i + 1); // 注意從i+1開始,元素不重復取
- path.pop_back(); // 回溯
- }
C++代碼
根據關于回溯算法,你該了解這些!給出的回溯算法模板:
- void backtracking(參數) {
- if (終止條件) {
- 存放結果;
- return;
- }
- for (選擇:本層集合中元素(樹中節點孩子的數量就是集合的大小)) {
- 處理節點;
- backtracking(路徑,選擇列表); // 遞歸
- 回溯,撤銷處理結果
- }
- }
可以寫出如下回溯算法C++代碼:
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
- result.push_back(path); // 收集子集,要放在終止添加的上面,否則會漏掉自己
- if (startIndex >= nums.size()) { // 終止條件可以不加
- return;
- }
- for (int i = startIndex; i < nums.size(); i++) {
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
- public:
- vector<vector<int>> subsets(vector<int>& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
- };
在注釋中,可以發現可以不寫終止條件,因為本來我們就要遍歷整顆樹。
有的同學可能擔心不寫終止條件會不會無限遞歸?
并不會,因為每次遞歸的下一層就是從i+1開始的。
本文轉載自微信公眾號「代碼隨想錄」,可以通過以下二維碼關注。轉載本文請聯系代碼隨想錄公眾號。