排列問題也要去重了!
全排列 II
力扣題目鏈接:https://leetcode-cn.com/problems/permutations-ii
給定一個可包含重復數字的序列 nums ,按任意順序 返回所有不重復的全排列。
示例 1:
- 輸入:nums = [1,1,2]
- 輸出:[[1,1,2], [1,2,1], [2,1,1]]
示例 2:
- 輸入:nums = [1,2,3]
- 輸出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
思路
如果對回溯算法基礎還不了解的話,我還特意錄制了一期視頻:帶你學透回溯算法(理論篇) 可以結合題解和視頻一起看,希望對大家理解回溯算法有所幫助。
這道題目和全排列的區別在與給定一個可包含重復數字的序列,要返回所有不重復的全排列。
這里又涉及到去重了。
在組合總和II 、子集II我們分別詳細講解了組合問題和子集問題如何去重。
那么排列問題其實也是一樣的套路。
還要強調的是去重一定要對元素經行排序,這樣我們才方便通過相鄰的節點來判斷是否重復使用了。
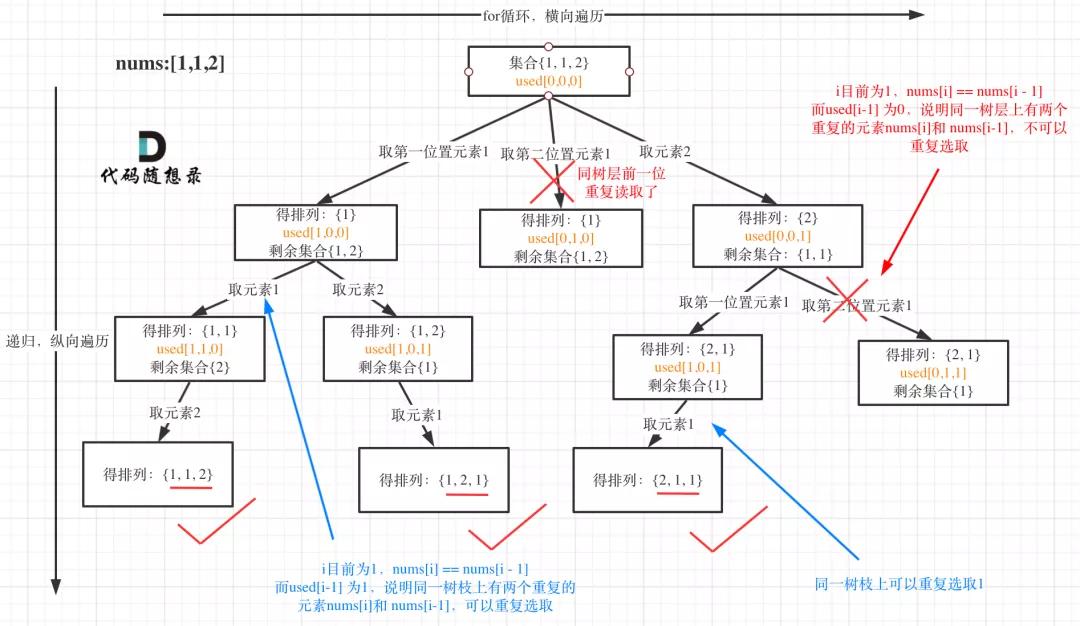
我以示例中的 [1,1,2]為例 (為了方便舉例,已經排序)抽象為一棵樹,去重過程如圖:
全排列II1
圖中我們對同一樹層,前一位(也就是nums[i-1])如果使用過,那么就進行去重。
一般來說:組合問題和排列問題是在樹形結構的葉子節點上收集結果,而子集問題就是取樹上所有節點的結果。
在46.全排列中已經詳解講解了排列問題的寫法,在40.組合總和II 、90.子集II中詳細講解的去重的寫法,所以這次我就不用回溯三部曲分析了,直接給出代碼,如下:
C++代碼
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking (vector<int>& nums, vector<bool>& used) {
- // 此時說明找到了一組
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- // used[i - 1] == true,說明同一樹支nums[i - 1]使用過
- // used[i - 1] == false,說明同一樹層nums[i - 1]使用過
- // 如果同一樹層nums[i - 1]使用過則直接跳過
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- if (used[i] == false) {
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- }
- public:
- vector<vector<int>> permuteUnique(vector<int>& nums) {
- result.clear();
- path.clear();
- sort(nums.begin(), nums.end()); // 排序
- vector<bool> used(nums.size(), false);
- backtracking(nums, used);
- return result;
- }
- };
拓展
大家發現,去重最為關鍵的代碼為:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
如果改成 used[i - 1] == true, 也是正確的!,去重代碼如下:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
- }
這是為什么呢,就是上面我剛說的,如果要對樹層中前一位去重,就用used[i - 1] == false,如果要對樹枝前一位去重用used[i - 1] == true。
對于排列問題,樹層上去重和樹枝上去重,都是可以的,但是樹層上去重效率更高!
這么說是不是有點抽象?
來來來,我就用輸入: [1,1,1] 來舉一個例子。
樹層上去重(used[i - 1] == false),的樹形結構如下:
全排列II2
樹枝上去重(used[i - 1] == true)的樹型結構如下:
全排列II
大家應該很清晰的看到,樹層上對前一位去重非常徹底,效率很高,樹枝上對前一位去重雖然最后可以得到答案,但是做了很多無用搜索。
總結
這道題其實還是用了我們之前講過的去重思路,但有意思的是,去重的代碼中,這么寫:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
和這么寫:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
- }
都是可以的,這也是很多同學做這道題目困惑的地方,知道used[i - 1] == false也行而used[i - 1] == true也行,但是就想不明白為啥。
所以我通過舉[1,1,1]的例子,把這兩個去重的邏輯分別抽象成樹形結構,大家可以一目了然:為什么兩種寫法都可以以及哪一種效率更高!
是不是豁然開朗了!!
本文轉載自微信公眾號「代碼隨想錄」,可以通過以下二維碼關注。轉載本文請聯系代碼隨想錄公眾號。