計算機出現之前，就有了算法。隨著計算機的誕生，需要更多的算法來釋放計算機強大的計算能力，算法是計算的核心，算法決定了計算機在解決問題時所采用的具體方式。

如果將計算機的存儲器理解為一種空間上的有限資源，那么算法消耗的計算時間則應該理解為一種時間上的有限資源。有限資源意味著它們存在各自的上界，即不可能存在無限快的計算機，也不可能存在完全免費的存儲器。

隨著摩爾定律走向瓶頸，在面對大型問題時，僅依靠硬件迭代可能愈發難以滿足海量的計算需求，選擇在時間和空間方面有效的算法，或許是有效提升實際收益的明智之舉。

那么，算法改進和硬件迭代相比，誰的收益更大？

[[431743]]

（來源：Pixabay）

算法改進與硬件迭代，究竟哪一種方式收益更高？一直以來都是學術界和工業界關注的熱點問題。來自麻省理工學院的相關人員前不久對這個問題作出了較為全面的回答。

為保證研究過程的嚴謹性，MIT 的研究人員全面分析了來自 57 部教科書和 1137 篇研究論文的相關數據，并撰文《How Fast Do Algorithms Improve?》，論文發表在 IEEE Proceedings 上，這是有史以來第一次對算法進展研究的綜合分析。

圖 | 相關論文（來源：IEEE Proceedings）

作者采用算法步驟分析的方式對算法展開研究，即在分析時間復雜度時保留常數項。對于給出明確算法步驟的參考論文，直接使用其結論。對于沒有給出明確算法步驟的參考論文，使用 “偽代碼” 進行重構。

研究內容主要包含以下幾方面工作：首先，作者系統地回顧了各算法的提出時間、改進時間，以及算法改進的總體趨勢；然后，作者針對不同的問題規模，對算法和硬件的改進率進行了對比分析；最后，作者利用算法和硬件改進率的對比分析結果，給出了問題規模及算法族跟改進率之間的相互關系。

算法回顧

依據待解決問題的類型進行劃分，作者將算法劃分為 113 個不同的算法族，對這些算法族的發展歷程進行了回顧，對改進算法進行了跟蹤分析，并重點關注那些有效提升性能的新算法。

這 113 個算法族包含了從 1940 年至今的大部分算法，每個算法族平均包含 8 種算法。判斷一個算法是否為有效的改進算法，其主要依據為判斷算法是否有效降低了所屬算法族在最壞情況下的漸進時間復雜度。

基于這一標準，作者得到 276 種初始算法和后續改進算法，并且每一個初始算法平均有 1.44 個后續的改進算法。上述研究成果可在作者團隊所創建的 “算法維基百科” 頁面（ http:// Algorithm-Wiki.org ）獲取更為詳細的信息。

如圖所示，作者將算法族作為基本單元，對算法的提出和改進歷程進行了歸納總結。其中，a）依據各算法族首次提出的時間，以十年為間隔，對算法族數目進行了統計；b）依據各算法族得到改進的時間，以十年為間隔，對算法族數目進行了統計；c）統計了所有算法族首次提出時間的漸進時間復雜度分布；d）表明通過算法改進，算法族的漸進時間復雜度在一年間得到降低的平均概率。

圖 | 算法回顧。（a）每個十年提出的新算法族數量；（b）已有算法族在每個十年間得到改進的數量；（c）算法族首次被提出時的算法漸進時間復雜度；（d）同一時間復雜度的算法提升至另一個時間復雜度的年平均概率。注：在（c）和（d）中”>n3”表示漸進時間復雜度高于多項式時間復雜度，但低于指數級時間復 

如上圖所示，算法族的改進速度在 1970’s 后有所放緩，作者認為其原因可能包括：

1）某些算法已達到理論最優，提升空間有限；

2）算法改進的邊際收益正在減少，改進成本提高；

3）近似算法更受研究者關注（不排除算法改進困難迫使研究者探索近似解）。

如圖 c）可以看到，其中 31% 的算法為指數漸進時間復雜度。而在圖 d）中正是將這些指數漸進時間復雜度的算法族改進到多項式時間復雜度更具深遠的意義，這些改進使得某些大型問題得以求解。

對比分析

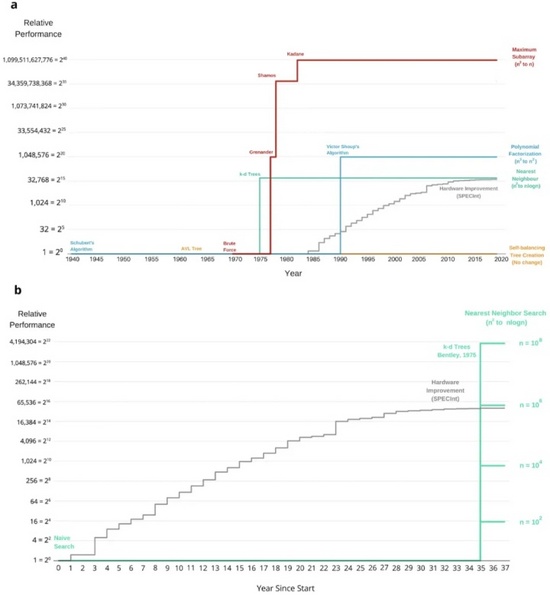
作者分析了算法族的性能隨新算法的發現，在時間上呈現出的發展趨勢。如圖所示，統計了四個算法族隨算法改進隨時間呈現的性能變化，對于 n=100 萬的問題規模，一些算法的改進效率已優于硬件提升的效率。并且算法改進和硬件迭代之間的一個明顯差別是：摩爾定律使得硬件性能呈現平穩上升的趨勢，而算法改進呈現明顯的不確定性。

圖 | 算法性能提升趨勢。（a）四個算法族隨算法改進隨時間呈現的性能變化；（b）硬件迭代隨時間產生的性能變化（來源：IEEE Proceedings） 

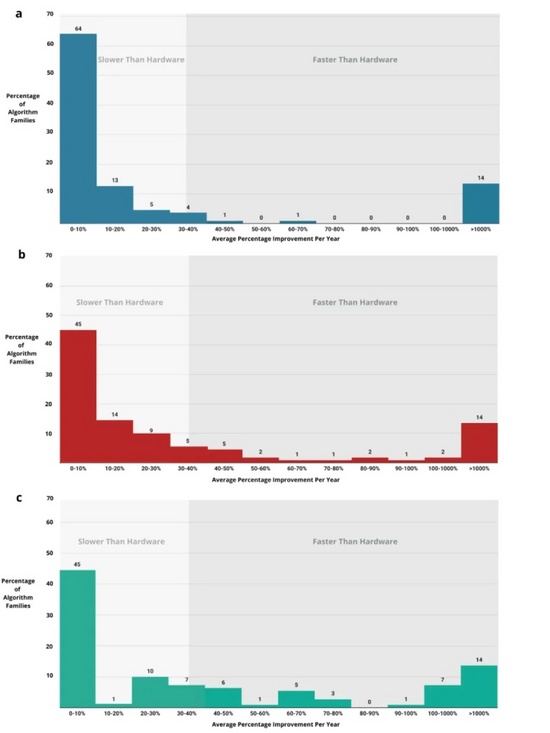
如圖，當擴展對 110 個算法族的分析時（如圖（a）所示)，對于數千量級的問題而言，只有 18% 的算法改進相較于硬件迭代具有更強的性能提升。隨著問題規模的不斷增加，算法改進帶來的性能提升就超過了硬件迭代。甚至有 14% 的算法族的改進率超過了 1000%，這部分性能的卓越提升大多受益于將指數漸進時間復雜度的算法改進至多項式漸進時間復雜度。當一個算法從指數漸進時間復雜度改進至多項式漸進時間復雜度時，它以任何硬件迭代都無法達到的方式改變了問題的可處理性。當問題增加至數十億乃至數萬億的規模時，算法改進比硬件迭代平均每年帶來的收益更高。

圖 | 基于漸近時間復雜度計算的 110 個算法族平均年改進率分布。（a）n=1000；（b）n=100萬；（c）n=10億（來源：IEEE Proceedings） 

這些發現表明，在大數據背景下，在對那些擁有海量數據的領域進行數據分析、機器學習時，算法改進顯得尤為重要。

作者發現不同算法族的改進歷程有極強的差異性，部分算法族改進進展緩慢，而又存在 14% 的算法經歷了比硬件迭代改進大幾個數量級的改進，極大地超越了摩爾定律。

總的來說，在面對問題規模較大時，算法改進帶來的收益大于硬件迭代（摩爾定律）。