移位的位數是負數,結果會怎樣?
有過編程經驗的同學,對于移位操作應該很熟悉了,日常工作中或多或少都有用到,當 移位位數是負數 或者 移位位數超過了 類型的最大二進制位時,和正常移位處理是不一樣的,下面將詳細說明這兩種情況,在此之前,先了解下正常的移位操作
正數的左移和右移
正數的左移是二進制位向左移動,右邊留空的位置補 0,右移是二進制位向右移動,左邊留空的位置補 0 ( 符號位為 0 )
- 左移
左移操作,最高位的符號位會出現 0 或 1 , 因此結果會出現正數和負數的情況
新建測試文件 base.cpp,代碼如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a << 2) = " << (a << 2) << endl;
- cout << "(a << 30) = " << (a << 30) << endl;
- return 0;
- }
執行 g++ -g -Wall -std=c++11 -o base base.cpp 命令編譯代碼,再執行 ./base 運行程序,結果如下
- (a << 2) = 28
- (a << 30) = -1073741824
上述代碼中,變量 a 的值為 7,對應的二進制是 0000 0000 0000 0000 0000 0000 0000 0111
左移 2 位:二進制向左移動 2 位,右邊補充 2 位 0 ,左邊丟棄超出的 2 位二進制, 結果是 0000 0000 0000 0000 0000 0000 0001 1100, 對應的十進制數是 28
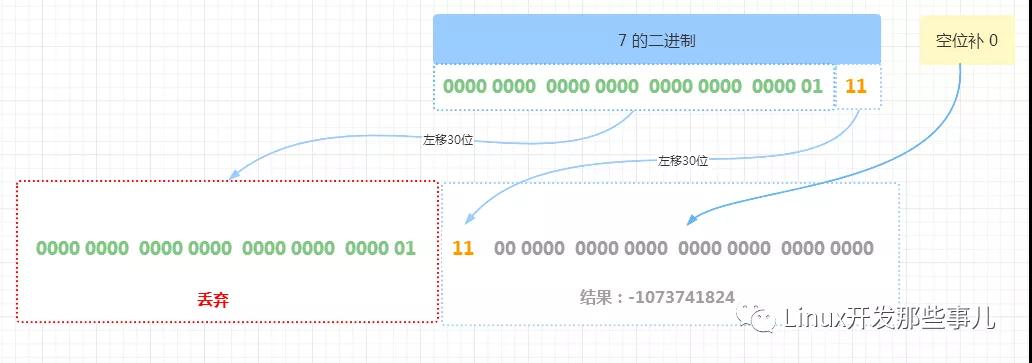
左移 30 位 的流程如下圖
由上圖可知,二進制向左移動 30 位后, 左邊 30 位二進制 0000 0000 0000 0000 0000 0000 0000 01 因超出被丟棄,同時最右邊剩下的 2 位二進制 11 左移 30 位,右邊空的位置補充 30 位 0,最終的結果是 1100 0000 0000 0000 0000 0000 0000 0000, 對應的十進制數是 -1073741824
可以看出,正數 7 左移 30 位后,二進制的符號位變成了 1 ,也即正數變成了負數了
- 右移
正數右移,最小為 0 , 不會出現負數,下面是右移的測試代碼
修改 base.cpp 文件,代碼如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> 1) = " << (a >> 1) << endl;
- cout << "(a >> 31) = " << (a >> 31) << endl;
- return 0;
- }
編譯并運行上面程序,結果如下:
- (a >> 1) = 3
- (a >> 31) = 0
上述實例代碼中,變量 a 的值為 7,對應的二進制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 1 位:二進制向右移動 1 位,左邊補充一位 0 ,右邊丟棄超出的一位二進制, 結果是 0000 0000 0000 0000 0000 0000 0000 0011, 對應的十進制數是 3
右移 31 位:二進制向右移動 31 位,左邊補充 31 位 0 ,右邊丟棄超出的 31 位二進制,結果是 0000 0000 0000 0000 0000 0000 0000 0000, 對應的十進制是 0
負數的左移和右移
負數的左移是二進制位向左移動,右邊留空的位置補 0,右移是二進制位向右移動,左邊留空的位置補 1 ( 符號位為 1 ),這一點跟正數是不一樣的
計算機中是用補碼的形式進行各種運算的,正數的補碼是其自身,負數的補碼是將其正數按位取反加 1
- 左移
負數左移,符號位可能會變成0,因此結果會出現正數和負數的情況,一直左移的話,最終會變成 0
修改 base.cpp文件,代碼如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t b = -3;
- cout << "(b << 1) = " << (b << 1) << endl;
- cout << "(b << 30) = " << (b << 30) << endl;
- return 0;
- }
編譯并運行上面程序,結果如下:
- (b << 1) = -6
- (b << 30) = 1073741824
上面代碼中,變量 b 的值為 -3,對應的二進制是 1111 1111 1111 1111 1111 1111 1111 1101
左移 1 位:整個二進制串向左移動 1 位,右邊補充 0 ,左邊丟棄超出的一位二進制,結果是 1111 1111 1111 1111 1111 1111 1111 1010,對應十進制數 -6
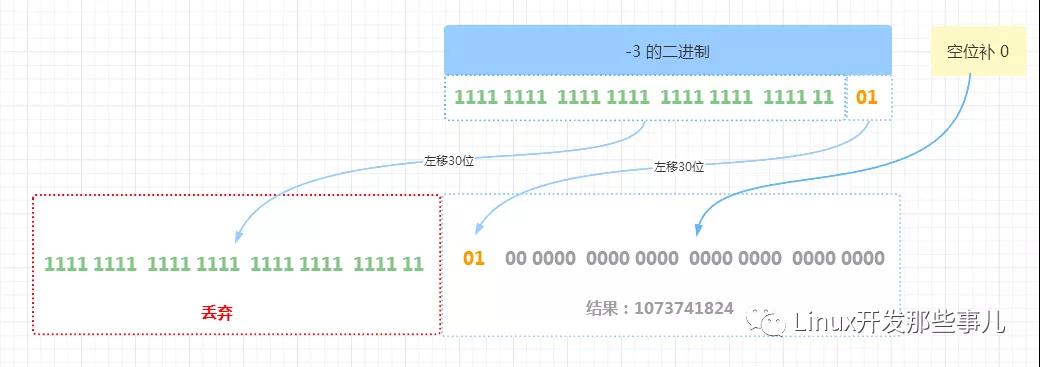
左移 30 位 的流程如下
由上圖可知,左移 30 位,左邊的 30 位二進制 1111 1111 1111 1111 1111 1111 1111 11 因超出數值最大位數而被丟棄,原來最右邊的 01 移到了最左邊,緊接著后面的 30 個空位全部補 0 ,最終的結果是 0100 0000 0000 0000 0000 0000 0000 0000 ,對應十進制是 1073741824
可以看出,負數 -3 左移 30 位后,二進制的符號位變成了 0 ,由開始的負數變成了正數了
- 右移
負數右移是在左邊補 1, 所以結果不會出現正數的情況,如果一直右移,最終二進制位會全部變成 1,即十進制的 -1 ( 二進制全 1 在補碼中表示 -1 )
修改 base.cpp,代碼如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t b = -3;
- cout << "(b >> 1) = " << (b >> 1) << endl;
- cout << "(b >> 31) = " << (b >> 31) << endl;
- return 0;
- }
編譯并運行上面程序,結果如下:
- (b >> 1) = -2
- (b >> 31) = -1
上面代碼中,變量 b 的值為 -3,對應的二進制是 1111 1111 1111 1111 1111 1111 1111 1101
右移 1 位:二進制位向右移動 1 位,左邊補充 1 ,右邊丟棄一位超出的二進制,結果為 1111 1111 1111 1111 1111 1111 1111 1110,對應的十進制是 -2
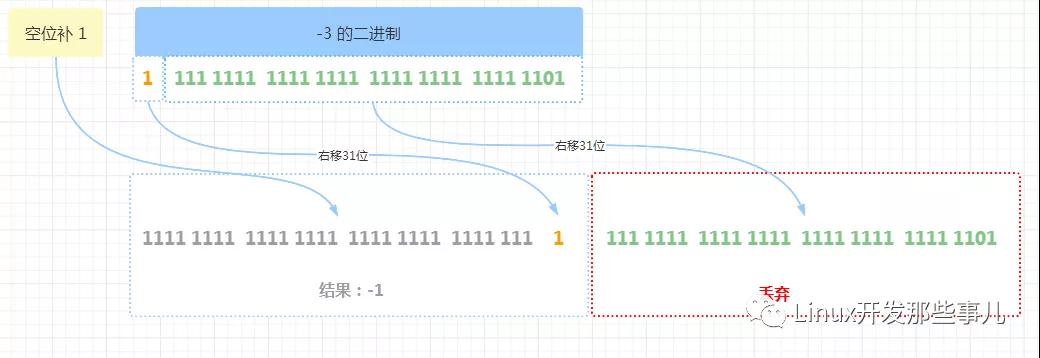
右移 31 位 的流程如下
根據上圖可知,右移 31 位,最右邊的 31 位二進制 1111 1111 1111 1111 1111 1111 1111 110 因超出數值最大位數而被丟棄, 原來左邊的 1 移到了最右邊,左邊補 31 位 1,最后結果為:1111 1111 1111 1111 1111 1111 1111 1111 , 對應的十進制數 -1
移位數超過類型最大位數
移位的位數大于等于數值類型的最大位數時,實際的移的位數是:移位的位數和該類型的最大位數做取模運算,余數就是要移的位數,不管左移還是右移,這種方法都適用
比如:類型為 int32_t,移位的位數是 34,實際移位的位數為:34 % 32 = 1
修改 base.cpp 文件,內容如下:
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> 32) = " << (a >> 32) << endl;
- cout << "(a >> 33) = " << (a >> 33) << endl;
- cout << "(a << 34) = " << (a << 34) << endl;
- return 0;
- }
編譯并執行,結果如下
- (a >> 32) = 7
- (a >> 33) = 3
- (a << 34) = 28
變量 a 的值為 7,對應的二進制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 32 位:因移位位數等于 int32_t 最大位數,所以實際移位數為 32 % 32 = 0,右移 0 位 表示沒有移位,所以結果還是 7
右移 33 位:移位位數大于 int32_t 最大位數,故實際移位數為 33 % 32 = 1,右移 1 位,左邊補 0 ,右邊丟棄超出的位,結果是: 0000 0000 0000 0000 0000 0000 0000 0011,對應的十進制是 3
左移 34 位:移位位數大于 32 ,實際移位數為 34 % 32 = 2,左移 2 位,右邊補 0 ,左邊丟棄超出的位,結果是:0000 0000 0000 0000 0000 0000 0001 1100,對應的十進制是 28
正常情況下,在移位數相同時,分幾次移位操作和單次移位操作的結果是一樣的, 比如:一個 int32_t 變量,值為 7, 7 << 1 << 2 和 7 << 3 的結果相同的
當移位數大于等于數值類型最大位數時,上述的結果是不一樣的,比如:一個 int32_t 變量,值為 7, 雖然 7 << 33 和 7 << 20 << 13 兩者移位數都是 33,但結果卻是不同的,前者是 14,而后者是 0
移位的位數是負值
當移位的位數是負值時,實際移位的位數是:用被移位數值類型的最大位數和移位位數相加,如果結果還是負數,結果繼續 加上被移位數值類型的最大位數,直到結果不為負數為止,此時的結果即為最終移位的位數
比如:被移位的數據類型是 int32_t,移位位數是 -31,最終移位的位數是:32 + ( -31 ) = 1
當移位位數是 -60,計算最終移位位數,32 + ( -60 ) = -28,由于結果還是負數,所以繼續相加,32 + ( -28 ) = 4,此次結果不為負數了,所以最終移位的位數是 4
修改 base.cpp 文件,內容如下:
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> -31) = " << (a >> -31) << endl;
- cout << "(a << -60) = " << (a >> -60) << endl;
- return 0;
- }
編譯代碼并執行,結果如下
- (a >> -31) = 3
- (a >> -60) = 0
變量 a 的值為 7,對應的二進制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 -31 位:移位數是負數,實際右移 32 + ( -31 ) = 1 位,結果為:0000 0000 0000 0000 0000 0000 0000 0011,對應的十進制是 3
右移 -60 位:移位數是負數,實際右移 32 + 32 + ( -60 ) = 4 位,結果為:0000 0000 0000 0000 0000 0000 0000 0000,對應的十進制是 0
小結
本文主要介紹了左移和右移操作,左移相當于乘以 2 的 N 次方,而右移相當于除以 2 的 N 次方,這里的 N 表示移位的位數,需要注意的是,當移位位數是負數或者大于等于類型最大位數時,編譯器對他們的處理和正常的移位是不一樣的