成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

程序員必備的幾種常見排序算法和搜索算法總結

作者： 徐小夕
開發 前端 算法
最近為了鞏固一下自己的算法基礎,又把算法書里的基本算法刷了一遍, 特地總結一下前端工程師需要了解的排序算法和搜索算法知識,雖然還有很多高深算法需要了解,

[[434262]]

前言

最近為了鞏固一下自己的算法基礎,又把算法書里的基本算法刷了一遍, 特地總結一下前端工程師需要了解的排序算法和搜索算法知識,雖然還有很多高深算法需要了解, 但是基礎還是要好好鞏固一下的.本文將以圖文的形式為大家介紹如下算法知識,希望在讀完之后大家能有所收獲:

  • 冒泡排序及其優化
  • 選擇排序
  • 插入排序
  • 歸并排序
  • 快速排序
  • 順序搜索
  • 二分搜索

正文

[[434263]]

我想對于每個前端工程師來說, 最頭疼的就是算法問題, 但是算法往往也是衡量一個人編程能力的一個很重要的指標.目前很多主流框架和庫都應用了大量的算法和設計模式,為了讓自己的段位更高,我們只能不斷的"打怪"(也就是刷算法)升級,才能成為"最強王者".

其實前端發展這么多年, 越來越偏向于精細化開發, 很多超級應用(比如淘寶,微信)都在追求極致的用戶體驗, 時間就是金錢,這要求工程師們不能像以前那樣,開發的程序只要能用就行, 我們往往還要進行更加細致的測試(包括單元測試, 性能測試等),就拿排序來說, 對于大規模數據量的排序, 我們采用冒泡排序肯定是要被瘋狂吐槽的,因為冒泡排序的性能極差(復雜度為O(n^2).在真實項目中我們往往不會采用冒泡排序,更多的會用快速排序或者希爾排序.關于排序算法性能問題我在

《前端算法系列》如何讓前端代碼速度提高60倍

有詳細介紹. 接下來就讓我們來一起學習如何實現文章開頭的幾個常用排序和搜索算法吧.

1. 冒泡排序及其優化

我們在學排序算法時, 最容易掌握的就是冒泡排序, 因為其實現起來非常簡單,但是從運行性能的角度來看, 它卻是性能最差的一個.

冒泡排序的實現思路是比較任何兩個相鄰的項, 如果前者比后者大, 則將它們互換位置.

為了更方便的展示冒泡排序的過程和性能測試,筆者先寫幾個工具方法,分別為動態生成指定個數的隨機數組, 生成元素位置序列的方法,代碼如下:

  1. // 生成指定個數的隨機數組 
  2. const generateArr = (num = 10) => { 
  3.   let arr = [] 
  4.   for(let i = 0; i< num; i++) { 
  5.     let item = Math.floor(Math.random() * (num + 1)) 
  6.     arr.push(item) 
  7.   } 
  8.   return arr 
  9. } 
  10.  
  11. // 生成指定個數的元素x軸坐標 
  12. const generateArrPosX = (n= 10, w = 6, m = 6) => { 
  13.   let pos = [] 
  14.   for(let i = 0; i< n; i++) { 
  15.     let item = (w + m) * i 
  16.     pos.push(item) 
  17.   } 
  18.   return pos 
  19. } 

有了以上兩個方法,我們就可以生成任意個數的數組以及數組項坐標了,這兩個方法接下來我們會用到.

我們來直接寫個乞丐版的冒泡排序算法:

  1. bubbleSort(arr = []) { 
  2.     let len = arr.length 
  3.     for(let i = 0; i< len; i++) { 
  4.       for(let j = 0; j < len - 1; j++) { 
  5.         if(arr[j] > arr[j+1]) { 
  6.           // 置換 
  7.           [arr[j], arr[j+1]] = [arr[j+1], arr[j]] 
  8.         } 
  9.       } 
  10.     } 
  11.     return arr 
  12.   } 

接下來我們來測試一下, 我們用generateArr方法生成60個數組項的數組, 并動態生成元素坐標:

  1. // 生成坐標 
  2. const pos = generateArrPosX(60) 
  3. // 生成60個項的數組 
  4. const arr = generateArr(60) 

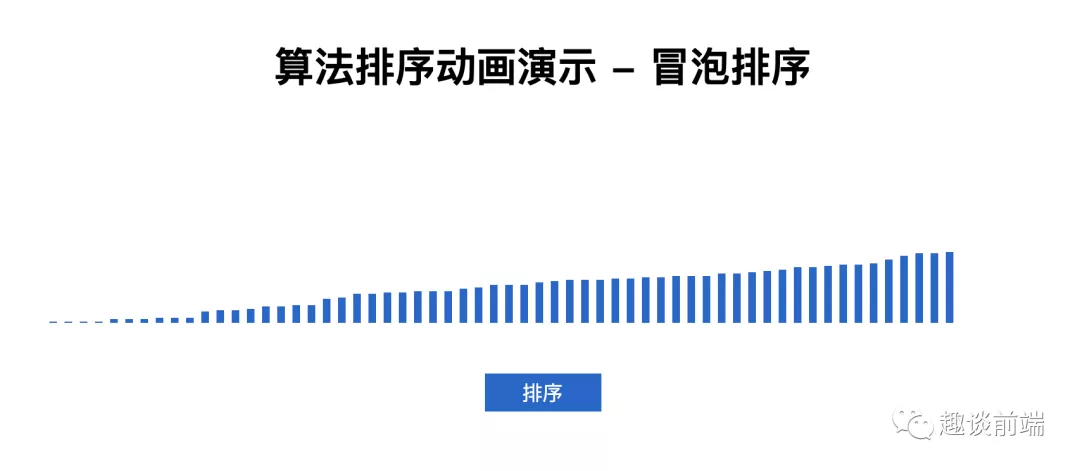
執行代碼后會生成下圖隨機節點結構:

有關css部分這里就不介紹了,大家可以自己實現.接下來我們就可以測試我們上面寫的冒泡排序了,當我們點擊排序時,結果如下:

可以看到數組已按照順序排好了,我們可以使用console.time來測量代碼執行所用的時間,上面"乞丐版"冒泡排序耗時為0.2890625ms.

我們深入分析代碼就可以知道兩層for循環排序導致了很多多余的排序,如果我們從內循環減去外循環中已跑過的輪數,就可以避免內循環中不必要的比較,所以我們代碼優化如下:

  1. // 冒泡排序優化版 
  2. bubbleSort(arr = []) { 
  3.   let len = arr.length 
  4.   // 優化 
  5.   for(let i = 0; i< len; i++) { 
  6.     for(let j = 0; j < len - 1 - i; j++) { 
  7.       if(arr[j] > arr[j+1]) { 
  8.         // 置換 
  9.         [arr[j], arr[j+1]] = [arr[j+1], arr[j]] 
  10.       } 
  11.     } 
  12.   } 
  13.   return arr 
  14. } 

經過優化的冒泡排序耗時:0.279052734375ms, 比之前稍微好了一丟丟, 但仍然不是推薦的排序算法.

2. 選擇排序

選擇排序的思路是找到數據結構中的最小值并將其放置在第一位,接著找到第二個最小值并將其放到第二位,依次類推.

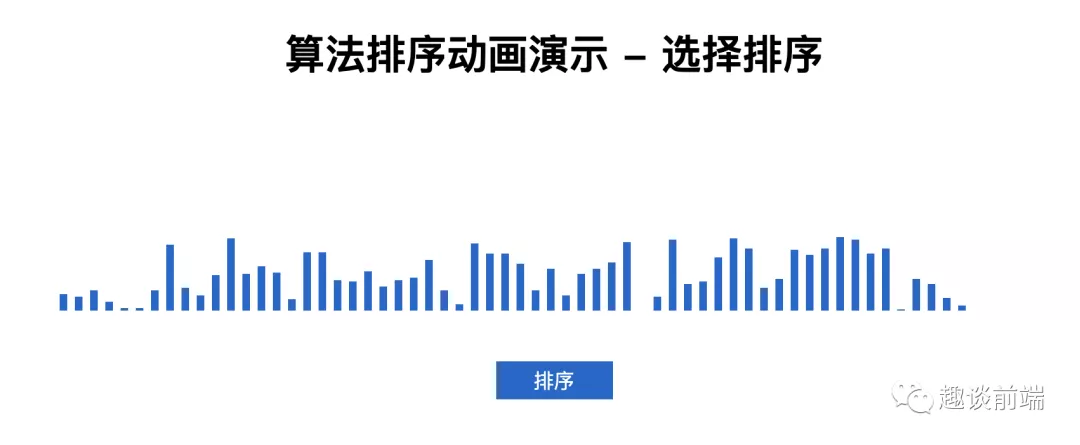
我們還是按照之前的模式,生成一個60項的數組, 如下:

選擇排序代碼如下:

  1. selectionSort(arr) { 
  2.     let len = arr.length, 
  3.         indexMin 
  4.     for(let i = 0; i< len -1; i++) { 
  5.       indexMin = i 
  6.       for(let j = i; j < len; j++){ 
  7.         if(arr[indexMin] > arr[j]) { 
  8.           indexMin = j 
  9.         } 
  10.       } 
  11.       if(i !== indexMin) { 
  12.         [arr[i], arr[indexMin]] = [arr[indexMin], arr[i]] 
  13.       } 
  14.     } 
  15.     return arr 
  16. } 

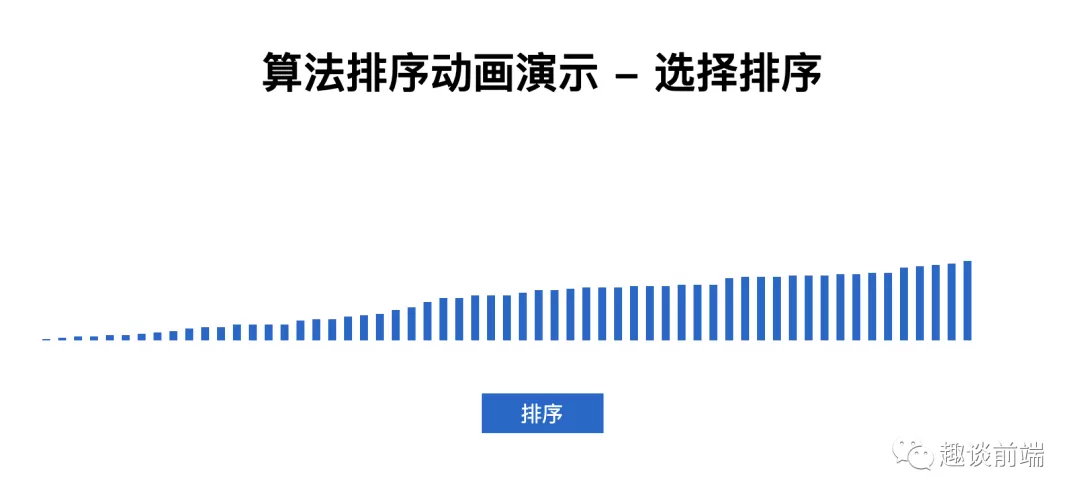
點擊排序時, 結果如下:

說明代碼運行正常, 可以實現排序, 控制臺耗時為: 0.13720703125ms, 明顯比冒泡排序性能要好.

3. 插入排序

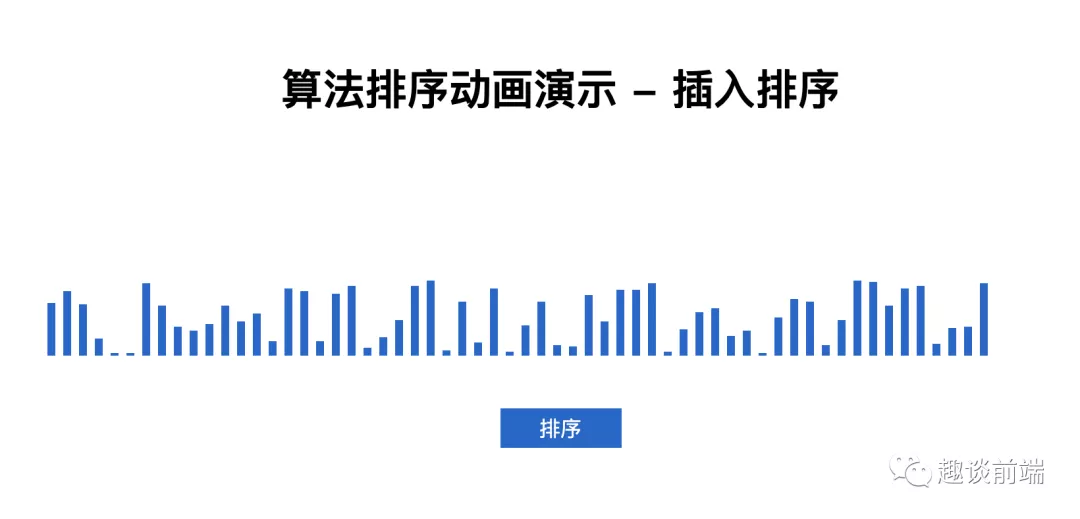
插入排序 的思路是每次排一個數組項,假定第一項已經排序,接著它和第二項比較, 決定第二項的位置, 然后接著用同樣的方式決定第三項的位置, 依次類推, 最終將整個數組從小到大依次排序.

代碼如下:

  1. insertionSort(arr) { 
  2.     let len = arr.length, 
  3.         j, 
  4.         temp; 
  5.     for(let i = 1; i< len; i++) { 
  6.       j = i 
  7.       temp = arr[i] 
  8.       while(j > 0 && arr[j-1] > temp) { 
  9.         arr[j] = arr[j-1] 
  10.         j-- 
  11.       } 
  12.       arr[j] = temp; 
  13.     } 
  14.  } 

執行結果如下:

控制臺打印耗時為:0.09912109375ms.

4. 歸并排序

歸并排序算法性能比以上三者都好, 可以在實際項目中投入使用,但實現方式相對復雜.

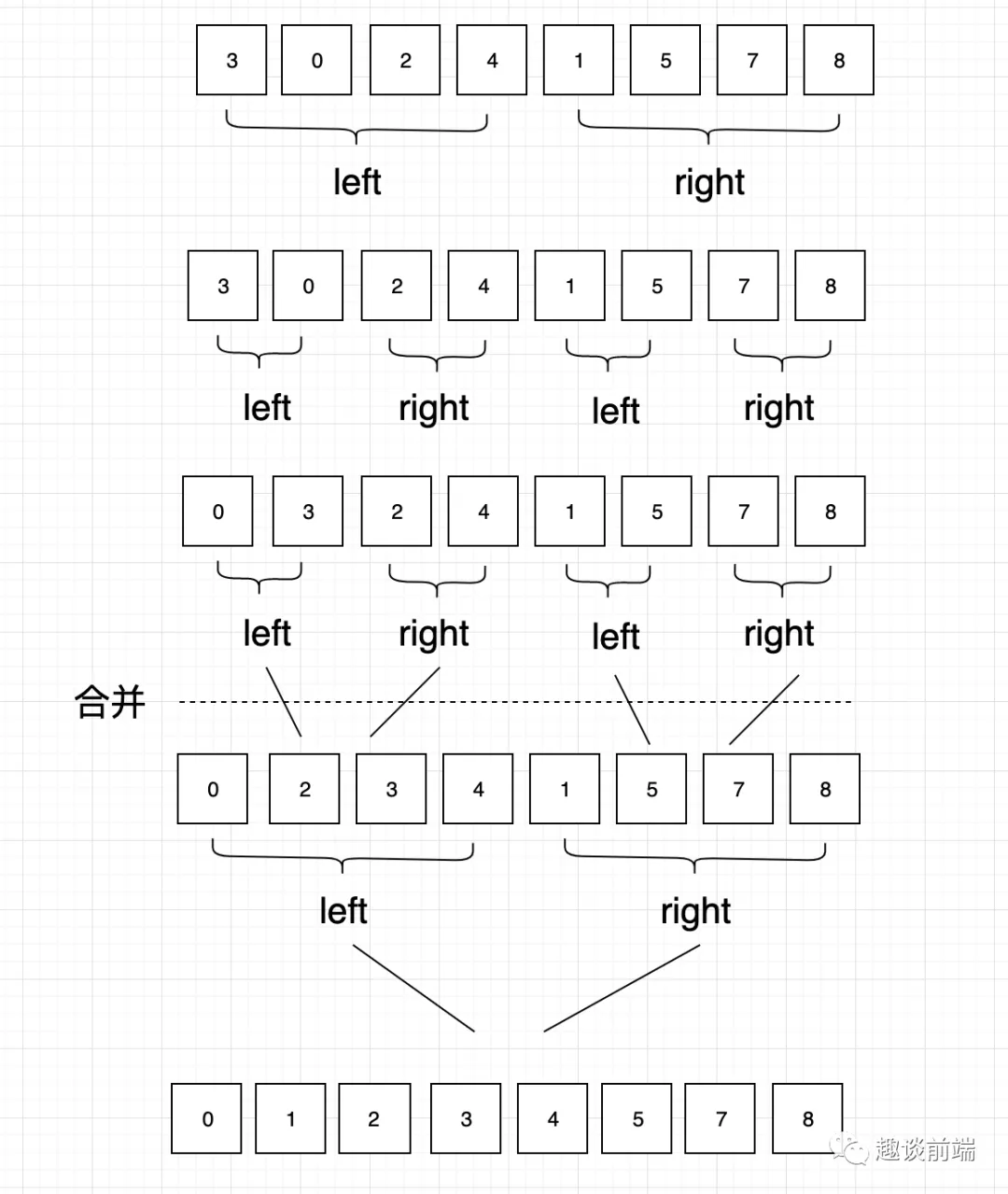
歸并排序是一種分治算法,其思想是將原始數組切分成較小的數組，直到每個小數組只有一個元素，接著將小數組歸并成較大的數組，最后變成一個排序完成的大數組。

其實現過程如下圖所示：

為了實現該方法我們需要準備一個合并函數和一個遞歸函數，具體實現如下代碼：

  1. // 歸并排序 
  2. mergeSortRec(arr) { 
  3.  let len = arr.length 
  4.  if(len === 1) { 
  5.    return arr 
  6.  } 
  7.  let mid = Math.floor(len / 2), 
  8.      left = arr.slice(0, mid), 
  9.      right = arr.slice(mid, len) 
  10.  return merge(mergeSortRec(left), mergeSortRec(right)) 
  11. } 
  12. // 合并方法 
  13. merge(left, right) { 
  14.     let result = [] 
  15.         l = 0, 
  16.         r = 0; 
  17.     while(l < left.length && r < right) { 
  18.       if(left[l] < right(r)) { 
  19.         result.push(left[l++]) 
  20.       }else { 
  21.         result.push(right[r++]) 
  22.       } 
  23.     } 
  24.     while(l < left.length) { 
  25.       result.push(left[l++]) 
  26.     } 
  27.     while(r < right.length) { 
  28.       result.push(right[r++]) 
  29.     } 
  30.     return result 
  31. } 

以上代碼中的遞歸作用是將一個大數組劃分為多個小數組直到只有一項，然后再逐層進行合并排序。如果有不理解的可以和筆者交流或者結合筆者畫的草圖進行理解。

5. 快速排序

快速排序是目前比較常用的排序算法，它的復雜度為O(nlog^n),并且它的性能比其他復雜度為O(nlog^n)的好，也是采用分治的思想，將原始數組進行劃分，由于快速排序實現起來比較復雜，這里講一下思路：

  1. 從數組中選擇中間項作為主元
  2. 創建兩個指針，左邊一個指向數組第一項，右邊一個指向數組最后一項，移動左指針直到我們找到一個比主元大的元素，移動右指針直到找到一個比主元小的元素，然后交換它們的位置，重復此過程直到左指針超過了右指針
  3. 算法對劃分后的小數組重復1，2步驟，直到數組完全排序完成。

代碼如下：

  1. // 快速排序 
  2. quickSort(arr, left, right) { 
  3.     let index 
  4.     if(arr.length > 1) { 
  5.       index = partition(arr, left, right) 
  6.       if(left < index - 1) { 
  7.         quickSort(arr, left, index -1) 
  8.       } 
  9.       if(index < right) { 
  10.         quickSort(arr, index, right) 
  11.       } 
  12.     } 
  13.   } 
  14. // 劃分流程 
  15. partition(arr, left, right) { 
  16.     let part = arr[Math,floor((right + left) / 2)], 
  17.         i = left, 
  18.         j = right 
  19.     while(i <= j) { 
  20.       while(arr[i] < part) { 
  21.         i++ 
  22.       } 
  23.       while(arr[j] > part) { 
  24.         j-- 
  25.       } 
  26.       if(i <= j) { 
  27.         // 置換 
  28.         [arr[i], arr[j]] = [arr[j], arr[i]] 
  29.         i++ 
  30.         j-- 
  31.       } 
  32.     } 
  33.     return i 
  34. } 

7. 順序搜索

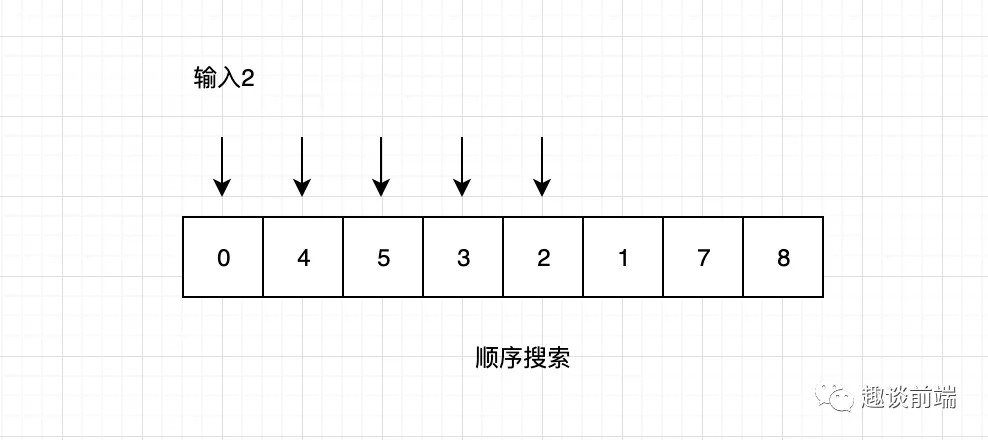
搜索算法也是我們經常用到的算法之一，比如我們需要查找某個用戶或者某條數據，不管是在前端還是在后端，都會使用搜索算法。我們先來介紹最簡單也是效率最低的順序搜索，其主要思想是將每一個數據結構中的元素和我們要查詢的元素做比較，然后返回指定元素的索引。

之所以說順序搜索效率低是因為每次都要從數組的頭部開始查詢，直到查找到要搜索的值，整體查詢不夠靈活和動態性。順序搜索代碼實現如下：

  1. sequentialSearch(arr, item) { 
  2.     for(let i = 0; i< arr.length; i++) { 
  3.       if(item === arr[i]) { 
  4.         return i 
  5.       } 
  6.     } 
  7.     return -1 
  8. } 

接下來我們看下面一種比較常用和靈活的搜索算法——二分搜索。

8. 二分搜索

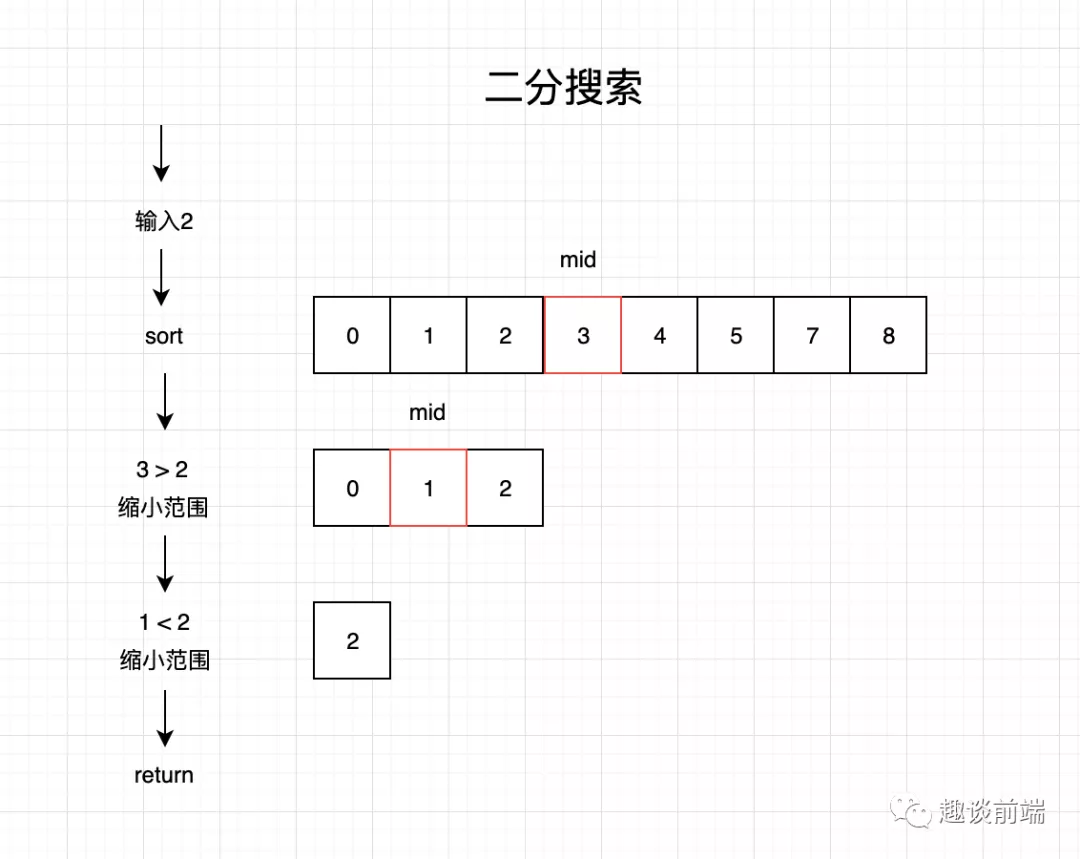
二分搜索的思想有點“投機學”的意思，但是它是一種有理論依據的“投機學”。首先它要求被搜索的數據結構已排序，其次進行如下步驟：

  1. 找出數組的中間值
  2. 如果中間值是待搜索的值，那么直接返回中間值的索引
  3. 如果待搜索的值比中間值小，則返回步驟1，將區間范圍縮小，在中間值左邊的子數組中繼續搜索
  4. 如果待搜索的值比選中的值大，則返回步驟1，將區間范圍縮小，在中間值右邊的子數組中繼續搜索
  5. 如果沒有搜到，則返回-1

為了方便理解筆者畫了如下草圖：

由上圖大家可以很容易的理解二分搜索的實現過程，接下來我們看下代碼實現：

  1. binarySearch(arr, item) { 
  2.     // 調用排序算法先對數據進行排序 
  3.     this.quickSort(arr) 
  4.  
  5.     let min = 0, 
  6.         max = arr.length - 1, 
  7.         mid, 
  8.         el 
  9.     while(min <= max) { 
  10.       mid = Math.floor((min + max) / 2) 
  11.       el = arr[mid] 
  12.       if(el < item) { 
  13.         min = mid + 1 
  14.       }else if(el > item) { 
  15.         max = mid -1 
  16.       }else { 
  17.         return mid 
  18.       } 
  19.     } 
  20.     return -1 
  21.   } 

其實還有很多搜索算法，筆者在js基本搜索算法實現與170萬條數據下的性能測試有具體介紹。

參考文獻：Learning JavaScript Data Structures and Algorithms

本文轉載自微信公眾號「趣談前端」

 

責任編輯：姜華 來源： 趣談前端
程序員排序算法搜索算法
相關推薦

2023-02-09 07:39:01

2021-09-04 23:40:53

算法程序員前端

2022-09-24 09:03:55

前端單元測試冒泡排序

2011-01-04 11:02:08

程序員

2019-03-29 09:40:38

數據結構算法前端

2020-10-14 08:32:08

算法遞歸面試

2012-08-20 09:26:17

程序員算法排列算法

2011-02-17 09:11:40

JavaScript算法

2014-07-01 09:43:55

程序員算法

2009-01-07 21:00:05

2023-05-30 07:58:01

谷歌搜索算法

2025-02-26 05:00:00

DFS算法遞歸

2020-12-08 05:52:28

js前端算法

2018-06-04 12:41:50

程序員貪心算法分析

2022-12-07 10:21:19

谷歌搜索技巧

2018-10-12 15:15:45

電商搜索算法

2023-11-30 08:09:05

2012-02-29 13:32:28

Java

2021-01-19 15:59:14

程序員算法書

2020-11-25 10:40:58

程序員技能開發者
點贊
收藏

51CTO技術棧公眾號

主站蜘蛛池模板： 日本一区二区在线视频 | 一级一级一级毛片 | 91在线视频网址 | 国产亚洲欧美另类一区二区三区 | 欧美日韩国产一区二区三区 | 手机av在线 | 亚洲成av | 国产欧美精品在线观看 | 久久综合狠狠综合久久综合88 | 日韩一区二区av | 懂色中文一区二区在线播放 | 成人免费视频网站在线看 | 国产精品免费一区二区 | 精品欧美一区二区在线观看视频 | 夜夜草天天草 | 欧美黄色片在线观看 | 国产无套一区二区三区久久 | 久久精品亚洲 | 亚洲va国产日韩欧美精品色婷婷 | 亚洲精品国产第一综合99久久 | 欧美黄色片| 狠狠操操| 国产不卡一区 | www.国产精品| 黄色免费av | 欧美人妖网站 | 国产你懂的在线观看 | 成人在线免费av | 91观看| 国产视频久久久 | 午夜专区 | 雨宫琴音一区二区在线 | 久久精品日产第一区二区三区 | 免费观看一级特黄欧美大片 | 久久av网 | 日本一区二区三区四区 | 精品国产一区一区二区三亚瑟 | 国产精品片aa在线观看 | 理论片午午伦夜理片影院 | 国产精品久久久久久久久久三级 | 免费在线性爱视频 |