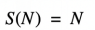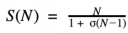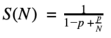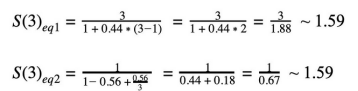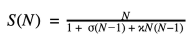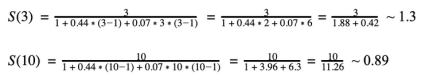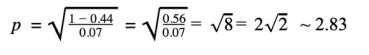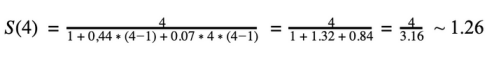軟件系統(tǒng)可擴(kuò)展性背后的爭(zhēng)用、一致性和數(shù)學(xué)

作者：李睿 2022-01-04 09:00:00

如何量化系統(tǒng)的可擴(kuò)展性？人們需要了解哪些定律能夠幫助估計(jì)軟件系統(tǒng)上線之后的擴(kuò)展能力。

【51CTO.com快譯】本文將介紹如何通過(guò)數(shù)學(xué)方程來(lái)描述系統(tǒng)——至少在某種程度上是這樣的。人們將熟悉諸如爭(zhēng)用、一致性和相關(guān)性延遲之類的術(shù)語(yǔ)。此外，還將展示可以幫助計(jì)算這三種機(jī)制對(duì)應(yīng)用程序影響的定律及其數(shù)學(xué)方程。

這篇文章側(cè)重于整體系統(tǒng)設(shè)計(jì)和架構(gòu)，并將嘗試回答“可以無(wú)限地?cái)U(kuò)展系統(tǒng)嗎?”這個(gè)問(wèn)題。

然而，為了充分理解這個(gè)主題，將首先回答一個(gè)更簡(jiǎn)單的問(wèn)題：什么是可擴(kuò)展性?

什么是可擴(kuò)展性?

可擴(kuò)展性的最佳定義之一可以在維基百科中找到，可以這樣引用：通過(guò)添加更多資源來(lái)處理越來(lái)越多的工作的系統(tǒng)屬性(...)

從這樣的聲明中，可以預(yù)期，如果軟件系統(tǒng)被認(rèn)為是可擴(kuò)展的，可以添加越來(lái)越多的資源(線程、CPU、節(jié)點(diǎn))，并可能處理任何增加的傳入流量。然而，這僅適用于理想世界。在令人失望的現(xiàn)實(shí)中，必須考慮以上提到的三個(gè)概念。在開(kāi)始解釋它為什么采用這種方式之前，先介紹有關(guān)線性可擴(kuò)展性的細(xì)節(jié)。

線性可擴(kuò)展性

一般來(lái)說(shuō)，這是想要實(shí)現(xiàn)的最佳情況。在這里，當(dāng)向系統(tǒng)添加資源時(shí)，它總是會(huì)導(dǎo)致其性能提升。更重要的是，可以無(wú)限期地做到這一點(diǎn)，而不會(huì)受到任何負(fù)面影響。可以用來(lái)計(jì)算線性可擴(kuò)展性影響的數(shù)學(xué)方程非常小且簡(jiǎn)單。

線性可擴(kuò)展性方程

S→整體任務(wù)的執(zhí)行時(shí)間整體提升

N→改進(jìn)的資源(線程、CPU、節(jié)點(diǎn))

現(xiàn)在可以看到，執(zhí)行時(shí)間的整體改進(jìn)只取決于改進(jìn)的資源，所以添加的資源越多，獲得的性能提升就越大。不幸的是，如上所述，在更復(fù)雜的系統(tǒng)中幾乎不可能出現(xiàn)這種情況。

在對(duì)線性可擴(kuò)展性進(jìn)行了簡(jiǎn)要介紹之后，可以進(jìn)一步探討其他主題，先從爭(zhēng)用開(kāi)始。

什么是爭(zhēng)用?

簡(jiǎn)單地說(shuō)，這是對(duì)共享資源訪問(wèn)權(quán)的競(jìng)爭(zhēng)。幾乎所有東西都可以是這樣的資源，從像CPU周期這樣的低級(jí)資源到像數(shù)據(jù)庫(kù)訪問(wèn)線程這樣的高級(jí)資源，甚至是更高的抽象資源(例如系統(tǒng)套接字)。

就像每場(chǎng)比賽一樣都只有一名獲勝者一樣，但更重要的是，在“獲勝者”勝出之后，其余的“參與者”必須等待，仍在利用和封鎖他們的資源，等待“獲勝者”完成任務(wù)之后，然后從頭開(kāi)始進(jìn)行比賽。

同樣，與任何其他比賽一樣，擁有的競(jìng)爭(zhēng)者越多，成為最終獲勝者所需的時(shí)間就越多。在面向軟件的世界中，這意味著當(dāng)將系統(tǒng)置于足夠的負(fù)載時(shí)，可以預(yù)期所有可接受的時(shí)間限制都將被打破。與此同時(shí)，系統(tǒng)將繼續(xù)利用其他地方可能需要的資源，這可能會(huì)導(dǎo)致越來(lái)越多的故障。

在任何類型的線程池的情況下，情況似乎更加復(fù)雜。在那里，可以看到最終有多個(gè)贏家的情況，因?yàn)橛泻芏嗑€程在線程池中，并且有多個(gè)輸家。此外，在這種情況下選擇下一個(gè)獲勝者的過(guò)程與特定的線程池實(shí)施密切相關(guān)。

現(xiàn)在，當(dāng)知道什么是爭(zhēng)用以及它可能如何影響應(yīng)用程序之后，繼續(xù)描述第一條定律。

什么是阿姆達(dá)爾定律?

阿姆達(dá)爾定律是由吉恩·阿姆達(dá)爾于1967年提出的。它描述了在資源得到改進(jìn)的系統(tǒng)中，在固定負(fù)載下任務(wù)執(zhí)行延遲的理論改進(jìn)——例如在多線程的情況下，這里指的是添加更多線程。

簡(jiǎn)而言之，它可以用來(lái)計(jì)算通過(guò)向系統(tǒng)添加更多資源而獲得的最大改進(jìn)。在這里至關(guān)重要的是，只有使用特定資源的代碼才能從這種資源改進(jìn)中獲益，這是一個(gè)非常合乎邏輯的結(jié)論，因此受到非獲益部分的執(zhí)行時(shí)間的限制。

例如：

如果想向系統(tǒng)添加更多線程，只有多線程的部分才能從這些操作中受益，而且將會(huì)受到單線程部分的執(zhí)行時(shí)間的限制。

阿姆達(dá)爾定律方程

S→整體任務(wù)執(zhí)行時(shí)間整體提升

σ→未受益于改進(jìn)資源的部分最初占用的執(zhí)行時(shí)間比例

N→改進(jìn)的資源(線程、CPU、節(jié)點(diǎn))

當(dāng)參數(shù)(σ)設(shè)置為0時(shí)，阿姆達(dá)爾定律將自身簡(jiǎn)化為線性可擴(kuò)展方程形式。

可以將σ替換為(1-p)，并在轉(zhuǎn)換后得到另一個(gè)與上述公式類似的方程：

p→受益于改進(jìn)資源的部分原先占用的執(zhí)行時(shí)間比例。

與p=1時(shí)的σ=0類似，阿姆達(dá)爾定律將自身簡(jiǎn)化為線性可擴(kuò)展方程形式。這兩種情況都描述了當(dāng)整個(gè)應(yīng)用程序受益于改進(jìn)資源時(shí)的最大潛在好處。

需要記住的是，這兩個(gè)方程是相等的，并且應(yīng)該為各自的數(shù)據(jù)返回相同的結(jié)果。將在示例中包括計(jì)算。

例子：

例如有一項(xiàng)工作運(yùn)行了9個(gè)小時(shí)。假設(shè)5小時(shí)長(zhǎng)的部分可以并行化和改進(jìn)，改進(jìn)后的速度將是之前的三倍。

現(xiàn)在知道：

N=3

p=5/9=0.56

σ=4/9=0.44

所以

如上所見(jiàn)，在這種情況下，將能夠比以前快0.59倍(大約6小時(shí)3分鐘)完成任務(wù)。

這里有兩個(gè)值得注意的事情：

(1)如果整個(gè)程序受益于系統(tǒng)資源改進(jìn)，S最多可以等于3;σ=0|p=1。

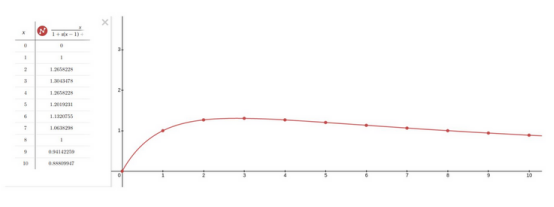
(2)受益部分越大，改善越大。

在上圖中，可以看到N從0到10的繪制圖，σ=0.44，這適用于阿姆達(dá)爾定律。

阿姆達(dá)爾定律和爭(zhēng)用

由于爭(zhēng)用使每個(gè)請(qǐng)求者的可用資源越來(lái)越少，從而限制了系統(tǒng)的并行化，因此可以看到，代碼庫(kù)越有爭(zhēng)議，改進(jìn)所產(chǎn)生的整體影響就越小。

在解釋了爭(zhēng)用、爭(zhēng)用對(duì)軟件的影響以及如何計(jì)算爭(zhēng)用之后，可以轉(zhuǎn)向需要討論的第二個(gè)概念。

什么是一致性?

一致性是指處理讀/寫的順序，以確保以合理的順序查看這兩個(gè)操作。它是整個(gè)系統(tǒng)設(shè)計(jì)中最重要的主題之一。這就是它在字母C下的CAP定理中找到了其表示的原因。兩個(gè)最重要的一致性模型是最終一致性和強(qiáng)一致性。還有其他一致性模型，但它們不那么重要。

什么是相關(guān)性?

相關(guān)性是一個(gè)與一致性密切相關(guān)的術(shù)語(yǔ)，是關(guān)于確保任何相關(guān)方在給定時(shí)刻看到處于相同狀態(tài)的同一特定數(shù)據(jù)段。對(duì)于在兩個(gè)或多個(gè)節(jié)點(diǎn)之間共享其部分狀態(tài)的所有系統(tǒng)來(lái)說(shuō)，這是一個(gè)至關(guān)重要的概念。

什么是相關(guān)性延遲?

如果相關(guān)性是為了確保對(duì)狀態(tài)特定部分的任何請(qǐng)求返回相同的值，那么相關(guān)性延遲可以被視為達(dá)到系統(tǒng)范圍一致性所需的時(shí)間。

這里值得一提的是，向系統(tǒng)添加更多節(jié)點(diǎn)會(huì)增加相關(guān)性延遲的時(shí)間。

如何選擇最優(yōu)的N?

這個(gè)答案很簡(jiǎn)單，但需要做一些數(shù)學(xué)運(yùn)算，本文中的大部分內(nèi)容也是如此。首先，可以將岡瑟定律視為一個(gè)函數(shù)S(N)，對(duì)于任何函數(shù)(實(shí)際上只是一部分)，可以計(jì)算S(N)具有最大值的點(diǎn)(N)。擁有這樣的價(jià)值提供了兩條非常重要的信息：

(1)知道在投入使用之前需要準(zhǔn)備多少資源。

(2)可以計(jì)算系統(tǒng)在當(dāng)前狀態(tài)下擴(kuò)展的范圍。

所有這一切都可以使用普通的計(jì)算器或紙筆實(shí)現(xiàn)，不包括計(jì)算機(jī)(取決于計(jì)算機(jī)的先進(jìn)程度)。

最優(yōu)N方程：

例子：

正在計(jì)算所需的節(jié)點(diǎn)數(shù)，以最大限度地改進(jìn)岡瑟定律示例中的數(shù)據(jù)。

σ=4/9=0.44

κ=0.07

如上所見(jiàn)，最佳節(jié)點(diǎn)數(shù)為2.83，但由于無(wú)法添加部分節(jié)點(diǎn)，因此會(huì)添加3個(gè)節(jié)點(diǎn)并最終得到p=3。

為了驗(yàn)證它，將計(jì)算S(4)，并查看使用4個(gè)節(jié)點(diǎn)而不是3個(gè)節(jié)點(diǎn)。將實(shí)現(xiàn)多大的改進(jìn)。需要記住，S(3)=1.3。

S(4)=1.26

如上所見(jiàn)，S(4)比S(3)小(稍微小一些)。

回答最后的問(wèn)題

可以無(wú)限擴(kuò)展系統(tǒng)嗎?當(dāng)然不是。

除非系統(tǒng)完全無(wú)狀態(tài)(這樣的情況很少)，否則只能將其擴(kuò)展到岡瑟定律所描述的程度。如果在該限制范圍內(nèi)添加更多資源，最終將降低系統(tǒng)性能，而不是提高性能。

即使在幾乎沒(méi)有相關(guān)性延遲的最佳情況下，最終也會(huì)受到阿姆達(dá)爾定律的限制，這仍然遠(yuǎn)遠(yuǎn)不能達(dá)到線性可擴(kuò)展性的程度，要實(shí)現(xiàn)這樣的可擴(kuò)展性，基本上必須沒(méi)有狀態(tài)，并且完全并行化的軟件沒(méi)有串行瓶頸。

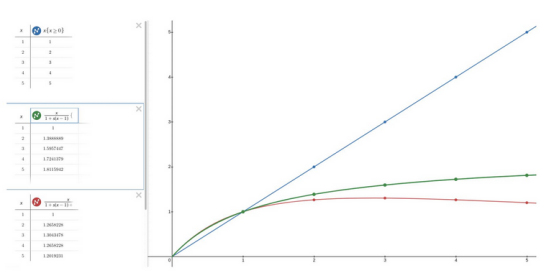
在上圖中，可以看到繪制的圖表：線性可擴(kuò)展性(藍(lán)線)、阿姆達(dá)爾定律(綠線)和通用的可擴(kuò)展性定律(紅線)從0到5。可以清楚地看到它們之間的差異，特別是它們與期望的可擴(kuò)展性(線性)之間的距離。當(dāng)然，N越大，這種差異就越明顯。根據(jù)研究，κ參數(shù)的值沒(méi)有通用規(guī)則。它的真正價(jià)值僅取決于系統(tǒng)的復(fù)雜性。