聊聊DP入門之整數拆分!
整數拆分
力扣題目鏈接:https://leetcode-cn.com/problems/integer-break
給定一個正整數 n,將其拆分為至少兩個正整數的和,并使這些整數的乘積最大化。返回你可以獲得的最大乘積。
示例 1:
- 輸入: 2
- 輸出: 1
- 解釋: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
- 輸入: 10
- 輸出: 36
- 解釋: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
說明: 你可以假設 n 不小于 2 且不大于 58。
思路
看到這道題目,都會想拆成兩個呢,還是三個呢,還是四個....
我們來看一下如何使用動規來解決。
動態規劃
動規五部曲,分析如下:
確定dp數組(dp table)以及下標的含義
dp[i]:分拆數字i,可以得到的最大乘積為dp[i]。
dp[i]的定義講貫徹整個解題過程,下面哪一步想不懂了,就想想dp[i]究竟表示的是啥!
確定遞推公式
可以想 dp[i]最大乘積是怎么得到的呢?
其實可以從1遍歷j,然后有兩種渠道得到dp[i].
一個是j * (i - j) 直接相乘。
一個是j * dp[i - j],相當于是拆分(i - j),對這個拆分不理解的話,可以回想dp數組的定義。
那有同學問了,j怎么就不拆分呢?
j是從1開始遍歷,拆分j的情況,在遍歷j的過程中其實都計算過了。那么從1遍歷j,比較(i - j) * j和dp[i - j] * j 取最大的。遞推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
也可以這么理解,j * (i - j) 是單純的把整數拆分為兩個數相乘,而j * dp[i - j]是拆分成兩個以及兩個以上的個數相乘。
如果定義dp[i - j] * dp[j] 也是默認將一個數強制拆成4份以及4份以上了。
所以遞推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的時候,為什么還要比較dp[i]呢?
因為在遞推公式推導的過程中,每次計算dp[i],取最大的而已。
dp的初始化
不少同學應該疑惑,dp[0] dp[1]應該初始化多少呢?
有的題解里會給出dp[0] = 1,dp[1] = 1的初始化,但解釋比較牽強,主要還是因為這么初始化可以把題目過了。
嚴格從dp[i]的定義來說,dp[0] dp[1] 就不應該初始化,也就是沒有意義的數值。
拆分0和拆分1的最大乘積是多少?
這是無解的。
這里我只初始化dp[2] = 1,從dp[i]的定義來說,拆分數字2,得到的最大乘積是1,這個沒有任何異議!
確定遍歷順序
確定遍歷順序,先來看看遞歸公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp[i] 是依靠 dp[i - j]的狀態,所以遍歷i一定是從前向后遍歷,先有dp[i - j]再有dp[i]。
枚舉j的時候,是從1開始的。i是從3開始,這樣dp[i - j]就是dp[2]正好可以通過我們初始化的數值求出來。
所以遍歷順序為:
- for (int i = 3; i <= n ; i++) {
- for (int j = 1; j < i - 1; j++) {
- dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
- }
- }
舉例推導dp數組
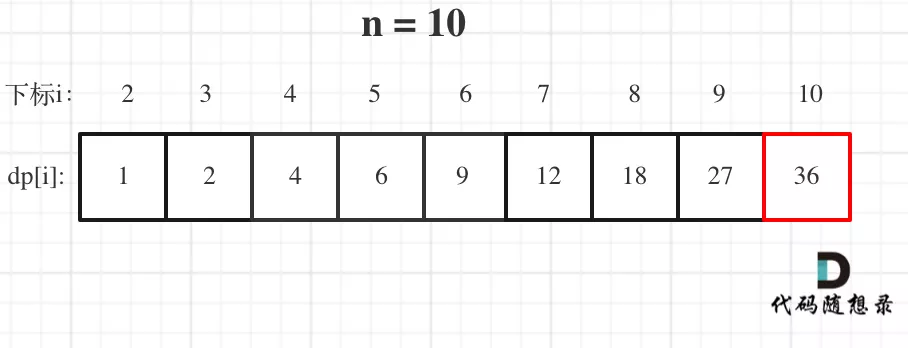
舉例當n為10 的時候,dp數組里的數值,如下:
整數拆分
以上動規五部曲分析完畢,C++代碼如下:
- class Solution {
- public:
- int integerBreak(int n) {
- vector<int> dp(n + 1);
- dp[2] = 1;
- for (int i = 3; i <= n ; i++) {
- for (int j = 1; j < i - 1; j++) {
- dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
- }
- }
- return dp[n];
- }
- };
貪心
本題也可以用貪心,每次拆成n個3,如果剩下是4,則保留4,然后相乘,但是這個結論需要數學證明其合理性!
我沒有證明,而是直接用了結論。感興趣的同學可以自己再去研究研究數學證明哈。
給出我的C++代碼如下:
- class Solution {
- public:
- int integerBreak(int n) {
- if (n == 2) return 1;
- if (n == 3) return 2;
- if (n == 4) return 4;
- int result = 1;
- while (n > 4) {
- result *= 3;
- n -= 3;
- }
- result *= n;
- return result;
- }
- };
總結
本題掌握其動規的方法,就可以了,貪心的解法確實簡單,但需要有數學證明,如果能自圓其說也是可以的。
其實這道題目的遞推公式并不好想,而且初始化的地方也很有講究,我在寫本題的時候一開始寫的代碼是這樣的:
- class Solution {
- public:
- int integerBreak(int n) {
- if (n <= 3) return 1 * (n - 1);
- vector<int> dp(n + 1, 0);
- dp[1] = 1;
- dp[2] = 2;
- dp[3] = 3;
- for (int i = 4; i <= n ; i++) {
- for (int j = 1; j < i - 1; j++) {
- dp[i] = max(dp[i], dp[i - j] * dp[j]);
- }
- }
- return dp[n];
- }
- };
這個代碼也是可以過的!
在解釋遞推公式的時候,也可以解釋通,dp[i] 就等于 拆解i - j的最大乘積 * 拆解j的最大乘積。看起來沒毛病!
但是在解釋初始化的時候,就發現自相矛盾了,dp[1]為什么一定是1呢?根據dp[i]的定義,dp[2]也不應該是2啊。
但如果遞歸公式是 dp[i] = max(dp[i], dp[i - j] * dp[j]);,就一定要這么初始化。遞推公式沒毛病,但初始化解釋不通!
雖然代碼在初始位置有一個判斷if (n <= 3) return 1 * (n - 1);,保證n<=3 結果是正確的,但代碼后面又要給dp[1]賦值1 和 dp[2] 賦值 2,這其實就是自相矛盾的代碼,違背了dp[i]的定義!
我舉這個例子,其實就說做題的嚴謹性,上面這個代碼也可以AC,大體上一看好像也沒有毛病,遞推公式也說得過去,但是僅僅是恰巧過了而已。
其他語言版本
Java
- class Solution {
- public int integerBreak(int n) {
- //dp[i]為正整數i拆分結果的最大乘積
- int[] dp = new int[n+1];
- dp[2] = 1;
- for (int i = 3; i <= n; ++i) {
- for (int j = 1; j < i - 1; ++j) {
- //j*(i-j)代表把i拆分為j和i-j兩個數相乘
- //j*dp[i-j]代表把i拆分成j和繼續把(i-j)這個數拆分,取(i-j)拆分結果中的最大乘積與j相乘
- dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
- }
- }
- return dp[n];
- }
- }
Python
- class Solution:
- def integerBreak(self, n: int) -> int:
- dp = [0] * (n + 1)
- dp[2] = 1
- for i in range(3, n + 1):
- # 假設對正整數 i 拆分出的第一個正整數是 j(1 <= j < i),則有以下兩種方案:
- # 1) 將 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多個正整數,此時的乘積是 j * (i-j)
- # 2) 將 i 拆分成 j 和 i−j 的和,且 i−j 繼續拆分成多個正整數,此時的乘積是 j * dp[i-j]
- for j in range(1, i - 1):
- dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
- return dp[n]
Go
- func integerBreak(n int) int {
- /**
- 動態五部曲
- 1.確定dp下標及其含義
- 2.確定遞推公式
- 3.確定dp初始化
- 4.確定遍歷順序
- 5.打印dp
- **/
- dp:=make([]int,n+1)
- dp[1]=1
- dp[2]=1
- for i:=3;i<n+1;i++{
- for j:=1;j<i-1;j++{
- // i可以差分為i-j和j。由于需要最大值,故需要通過j遍歷所有存在的值,取其中最大的值作為當前i的最大值,在求最大值的時候,一個是j與i-j相乘,一個是j與dp[i-j].
- dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]))
- }
- }
- return dp[n]
- }
- func max(a,b int) int{
- if a>b{
- return a
- }
- return b
- }
Javascript
- var integerBreak = function(n) {
- let dp = new Array(n + 1).fill(0)
- dp[2] = 1
- for(let i = 3; i <= n; i++) {
- for(let j = 1; j < i; j++) {
- dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
- }
- }
- return dp[n]
- };