從盤古開天辟地說起為什么 Flink CP 能實現精確一次之二

作者：antigeneral了呀 2022-02-20 10:47:54

大數據數據倉庫

本文主要講了一個分布式應用異步做一個全局一致性快照的機制。

為什么我要把這段話放在最前面呢?因為博主有了大發現，博主在總結學習的過程中，總結了除了 Flink CP、Chandy-Lamport 全局一致性快照算法之外的一種通用全局一致性快照算法!!!。

這套通用算法包含 Chandy-Lamport 算法 ≈ Flink 非對齊 CP 算法包含 Flink 對齊 CP 算法。

可能這一套通用算法之前已經有人提過了，但是博主是自己在總結 Flink CP、Chandy-Lamport 算法的過程中，逆推總結出來的，并沒有借助外力!!!

1.前言

對于很多做離線或者實時數倉的小伙伴來說，我先問幾個問題，看看小伙伴萌能回答上來嗎?

? 你知道狀態是什么嗎?在離線數據開發的經歷中，你碰到過狀態的概念嗎?
? 為什么離線數倉不需要狀態，實時數據開發中老是提到狀態的概念?
? Flink 中的狀態、狀態后端、全局一致性快照(Checkpoint\Savepoint) 的作用都是什么，這三個概念的關聯又是什么?
? Flink 是通過什么機制來做 Checkpoint 的?為什么這套機制能夠做到故障恢復呢?
? Flink Checkpoint 是基于 Chandy-Lamport 算法的，但是 Flink 的實現相比 Chandy-Lamport 算法之間又有哪些優點、缺點?
? Flink Checkpoint 用到了 barrier，為什么用了 barrier 做的快照就能保證全局一致性快照的正確性?barrier 到底起到了什么作用?
? Flink 對齊 Checkpoint 和非對齊 Checkpoint 的區別是什么?非對齊 Checkpoint 也能保障精確一次嗎?

小伙伴們思考一下，都能回答上來么，如果對于某些問題你還有疑問，樓主會通過本篇文章幫你解答這些問題，理清這些概念!

由于本文內容較多，所以博主將本文分為上，中，下三集，本文是中，三集內容是有連接關系的，如果小伙伴在看本文的過程中對有些概念不清楚，可以跳轉到上文進行查看：

本文最主要的內容就是解釋了：

一個分布式應用是怎么異步做一個全局一致性快照?

2.名詞解釋

? Single-Token conservation：一個最常見的分布式應用，單 Token 流轉分布式應用
? Process：指分布式應用中的進程，舉個 Flink 中的例子就是 TaskManager
? Channel：指分布式應用中進程之間的傳輸通道，舉個 Flink 中的例子就是 TaskManager 之間傳輸數據的網絡傳輸通道

3.分布式應用全局一致性快照要記錄的狀態內容

首先在分析一個復雜的大數據應用的全局一致性快照之前，我們先以最簡單的分布式應用為例。

Single-Token conservation：其有 p 和 q 兩個進程，p 可以通過 Channel pq(記為 Cpq) 向 q 發消息，q 可以通過 Channel qp(記為 Cqp) 向 p 發消息，其中有一個叫 token 的消息，在這個系統中一直不停的傳輸流轉，從 p 到 q，再從 q 到 p。

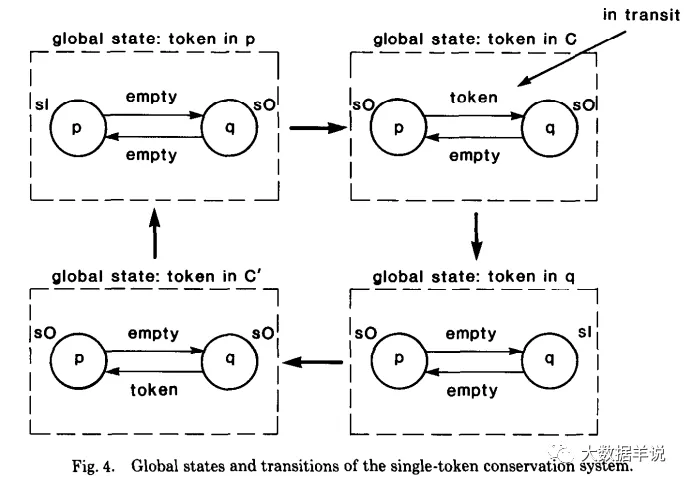
? 首先我們來分析這個應用中，全局一致性快照應該包含哪些內容?
? 結論：全局一致性快照 = Process 狀態 + Channel 狀態。
? 原因：以上面的四幅圖為例，每一幅圖代表一個時刻，如果我們以拍照這種方式做全局一致性快照來理解時，那么同一時刻，Process 和 Channel 同時都會存在數據，這些數據都是作為全局一致性快照的一部分內容。

使用上述的這個結論，我們可以得到上圖 Single-Token conservation 示例中的全局一致性快照 S = S(p) + S(Cpq) + S(q) + S(Cqp)

其中：

S：全局一致性快照
S(p)：p 進程的狀態
S(Cpq)：p 進程到 q 進程的 Channel 狀態
S(q)：q 進程的狀態
S(Cqp)：q 進程到 p 進程的 Channel 狀態

這里就碰到了我們要分析的關鍵問題：做全局一致性快照時，小伙伴萌都容易理解S(p)，S(q)這兩個，因為這兩份狀態數據就真實的存在我們的分布式應用中，但是S(Cpq)，S(Cqp)這兩個怎么理解呢?這些數據都是在網絡中傳輸啊，我們做全局一致性快照時用啥方法才能把這些數據也記錄下來呢?接下來詳細講講博主的理解

4.Process 狀態記錄的內容

記錄和實際業務相關的狀態內容。舉例：id 去重就存儲歷史所有的 id 就可以了。

5.Channel 狀態記錄的內容

還是以前文的 Single-Token conservation 為例：

token 在 p 時(對應第一張圖)，這時的全局一致性快照為：

S(token-in-p) = S(p-token-in-p) + S(Cpq-token-in-p) + S(q-token-in-p) + S(Cqp-token-in-p)

其中：

S(token-in-p)：token 在 p 時，做的全局一致性快照
S(p-token-in-p)：token 在 p 時，p 進程的狀態
S(Cpq-token-in-p)：token 在 p 時，p 進程到 q 進程的 Channel 狀態
S(q-token-in-p)：token 在 p 時，q 進程的狀態
S(Cqp-token-in-p)：token 在 p 時，q 進程到 p 進程的 Channel 狀態

其中 S(p-token-in-p) 好理解，做快照時，token 還沒有從 p 發出去，p 肯定知道 token 還在 p;但是站在 Cpq 做狀態時來說：Cpq 做狀態時，怎么保障 Cpq 知道 token in p?

在分析上面這個問題前，博主先使用數學的方式分析一下 S(Cpq) 到底記錄了哪些內容。

? 第一步：定義變量

n：在 p 的狀態記錄前，p 記錄的 p 發往 Cpq 的 msg 數;
n′：在 Cpq 的狀態記錄前，Cpq 記錄的 p 發往 Cpq 的 msg 數;
m：在 q 的狀態記錄前，q 記錄的 q 從 Cpq 中接收到的 msg 數;
m′：在 Cpq 的狀態記錄前，Cpq 記錄的 q 從 Cpq 中接收到的 msg 數;

? 第二步：提出假設

假設 Channel 和 Process 一樣，也可以自主的去將做快照時 Channel 中進行網絡傳輸的數據作為狀態保存下來;對應到上述案例中就是 Cpq 可以主動的將做好的 S(Cpq) 狀態保存下來;

? 第三步：先說結論

Cpq 記錄S(Cpq)時，必然會有 n = n' ≥ m = m';
一個 Channel 要記錄的狀態是，它 sender 記錄自己狀態之前 channel 所接收到 sender 發的的 msg 列表，再減去 receiver 記錄自己狀態之前 channel 已經發給 receiver 的 msg 列表，減去的之后的 msg 就是還在 Channel 中的數據，這些數據是需要 Channel 作為狀態記錄下來的。
而如果 n′ = m′，那么 Channel c 中要記錄的 msg 列表就是 empty 列表。如果 n′ > m′，那么要記錄的列表是 (m′+1),…n′ 號消息對應的 msg 列表。

? 第四步：給出證明

首先：n = n'，利用反證法：如果 n != n'，則會有：

1.n > n' 時，假設：

n = 10(p 記錄狀態前，p 記錄 p 發往 Cpq msg 數為 10(msg 編號 1 - 10));
n' = 7(Cpq 記錄狀態前，Cpq 記錄 p 發往 Cpq 的 msg 數為 7(msg 編號 1 - 7));
那么假設 token 這條 msg 的編號為 9，就會出現 p 記錄的狀態為S(p-token-in-Cpq)，Cpq 記錄的狀態為S(p-token-in-p)，實際這是不符合全局一致性快照的要求的;

2.n < n' 時，假設：

n = 7(p 記錄狀態前，p 記錄 p 發往 Cpq msg 數為 7(編號 1 - 7));
n' = 10(Cpq 記錄狀態前，Cpq 記錄 p 發往 Cpq 的 msg 數為 10(編號 1 - 10));
那么假設 token 這條 msg 的編號為 9，就會出現 p 記錄的狀態為S(p-token-in-p)，Cpq 記錄的狀態為S(p-token-in-Cpq)，實際這是不符合全局一致性快照的要求的;

3.n = n' 時，假設：

p 做出S(p-token-in-p)的狀態時，因為 n = n'，這就代表 p 沒有把 token 發出去，Cpq 也沒有接受到 token，Cpq 就知道 token 沒有發過來，則只有這種情況可以滿足S(Cpq-token-in-p);

其次：m = m'，同樣利用反證法可以得到，下文只舉 m > m' 的案例：

1.m > m' 時：

n = n' = m = 10(q 記錄狀態前，Cpq 記錄 q 從 Cpq 接收到的 msg 數為 10(編號 1 - 10));
m' = 7(Cpq記錄狀態前，Cpq 記錄的 q 從 Cpq 接收到的 msg 數為 7(編號 1 - 7));
那么假設 token 這條 msg 的編號為 9，就會出現 Cpq 記錄的狀態為S(Cpq-token-in-Cpq)，q 記錄的狀態為S(q-token-in-p)，實際這是不符合全局一致性快照的要求的;

最后：n' ≥ m' and n ≥ m：同樣可以利用反證法得到，此處不再舉例。

4.? 第五步：解答 2.4 節提出的 Cpq 怎么知道 token in p 的問題

通過 n = n' ≥ m = m' 其實就可以推論出 Cpq 一定會知道 token in p。

為了幫大家更容易的理解一個分布式應用包含的全局一致性快照包含的數據內容，接下來我用偽代碼描述一下，會比文字更好理解~

6.偽代碼描述一個分布式應用全局一致快照包含的數據內容

偽代碼如下：

// S_all 即一個分布式應用的全局一致性快照
S_all = null;

// 假設總共有 x 個 Process，S_all 先把所有 Process 的狀態記錄下來
for (int i = 1; i <= x; i++) {
  // 第 i 個 Process 的狀態為 S_P_i，直接按照 += 寫，勿噴
  S_all += S_P_i;
}

// 假設總共有 y 個 Channel，S_all 把所有 Channel 的狀態記錄下來
for (int i = 1; i <= y; i++) {
  // 1. S_C_i：第 i 個 Channel 的狀態
  // 2. m_i：第 i 個 Channel 做快照前，發往下游 Process 的消息（數據）編號，m_i 其實就是上文變量中的 m
  // 3. n_i：第 i 個 Channel 做快照前，接受上游 Process 的消息（數據）編號，n_i 其實就是上文變量中的 n
  // 4. 需要注意，每一個 Channel 的 m_i 和 n_i 的數值都可能是不一樣的
  // 5. Message[m_i + 1] ：代表編號為 m_i + 1 的那條消息（數據）。舉例 Message[0] 代表編號為 0 的那條消息（數據）
  S_C_i = Message[m_i + 1] + ... + Message[n_i];
  
  S_all += S_C_i;
}

// 狀態做完了

7.怎樣去記錄 Channel 的狀態?

通過上面的分析，我們已經討論得到了S(Cpq)都包含了什么內容，并且其之間要滿足什么樣的數學關系。但是在現實實際生活中，消息在 Channel 上傳輸(光纖上傳輸)時，我們是無法記錄這些消息作為 Channel 的狀態的。

那么有沒有什么思路可以讓我們也能夠去記錄 Channel 的消息呢?

當然有。

因為只要我們分布式應用的傳輸這些消息的光纖沒有被挖斷，消息終究會通過 Channel 到達 Process 的，因此我們就可以自然的想到其實可以在消息傳輸終點的 Process 去記錄這些消息作為 Channel 的狀態。對應到上述的 Single-Token conservation 案例來說，我們可以在 q 中記錄 Channel pq 的S(Cpq)，在 p 中記錄 Channel pq 的S(Cqp)。

如果是按照這個思路去分析的話，上面那段偽代碼就可以簡化為下面這樣：

// S_all 即全局一致性快照
S_all = null;

// 假設總共有 x 個 Process
for (int i = 1; i <= x; i++) {
  // S_i_all：第 i 個 Process 要記錄的所有狀態
  S_i_all = null;
  
  // S_P_i：第 i 個 process 的狀態
  S_i_all += S_P_i; // 【直接按照 += 寫，勿噴】
  
  // 第 i 個 Process 總共有 y 個輸入 channel，下文中 j 即指代第 i 個 Process 的第 j 個上游 Channel
  for (int j = 1; j <= y; j++) {
    // 1.S_C_j：第 j 個 Channel 的狀態
    // 2.m_j：第 j 個 Channel 做快照前，發往下游 Process 的消息（數據）編號
    // 3.n_j：第 j 個 Channel 做快照前，接受上游 Process 的消息（數據）編號
    S_C_j = Message[m_j + 1] + ... + Message[n_j];

    S_i_all += S_C_j;
  }
  
  S_all += S_i_all;
}

// 狀態做完了

解釋一下上面的偽代碼：

1.S_all：所有的進程記錄的狀態之和，即所有S_i_all之和

2.S_i_all：每一個進程要記錄的所有狀態之和

3.Process i 在做S_i_all其實只有一個變量在做快照時是不知道到的，那就是 n_j(即第 i 個 channel 做快照前，接受到 j(上游) 的消息個數)

S_P_i是 Process 自己的狀態，所以是明確已知的
S_C_j是 Channel 狀態，由Message[m_j + 1] + ... + Message[n_j]組成，其中 m_j 的含義是這個 Channel j 在做快照時發給當前 Process i 的消息編號，前文已經介紹到 m = m'，即 m_j 值就等于是是當前 Process i 在做S_P_i時，接收到上游 Channel 的消息編號，所以 m_j 是明確已知的。但是 Process i 在做上游 Channel j 快照時 n_j 是無法獲取到的。

那么 Process i 在做S_C_j如何獲取到 n_j 呢?

這里我們就可以想到 n = n'：

因為 n = n'，所以 n_j 的值就等于 Channel j 的上游 Process 在做快照時，Process 發往 Channel j 的消息個數;
所以我們可以認為 n_j 是 Channel j 的輸入 Process 在做快照時已知的一個值，則只需要這個 Process 把這個值發給 Process i 就行;
Channel j 的輸入 Process 告知 Process i 的方式其做完快照之后，直接發一個 marker 下去，這個 marker 不會對計算有任何影響(即不會對狀態產生任何影響)，marker 只是一個標識，當 Process i 接受到這個 marker 時，就知道 n_j 的具體值了。

大家注意到了沒，這個 marker 其實就對應到了 Flink 中 Checkpoint 的 barrier。

8.總結