一文搞懂二分查找算法!
基本介紹
二分搜索(折半搜索)是一種在有序數組中查找某一特定元素的搜索算法。
從定義可知,運用二分搜索的前提是數組必須是排好序的,另外,輸入并不一定是數組,也有可能是給定一個區間的起始和終止的位置。
他的時間復雜度是 O(lgn),非常高效。
基本特點
他的缺點要求待查找的數組或者區間是排好序的。
如果對數組進行動態的刪除和插入操作并完成查找,平均復雜度會變為 O(n)。
因此,當輸入的數組或者區間是排好序的,同時又不會經常變動,而要求從里面找出一個滿足條件的元素的時候,二分搜索就是最好的選擇。
解題思路
二分搜索一般化的解題思路如下:
- 從已經排好序的數組或區間中取出中間位置的元素,判斷該元素是否滿足要搜索的條件,如果滿足,停止搜索,程序結束。
- 如果正中間的元素不滿足條件,則從它兩邊的區域進行搜索。由于數組是排好序的,可以利用排除法,確定接下來應該從這兩個區間中的哪一個去搜索。
- 通過判斷,如果發現真正要找的元素在左半區間的話,就繼續在左半區間里進行二分搜索。反之,就在右半區間里進行二分搜索。
二分查找的解題框架
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
//計算 mid 時需要技巧防止溢出,建議寫成: mid = left + (right - left) / 2
int mid = (right + left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}常見解法
遞歸解法
假設我們要從一個排好序的數組里 {1, 3, 4, 6, 7, 8, 10, 13, 14} 查看一下數字 7 是否在里面,如果在,返回它的下標,否則返回 -1。
遞歸寫法的代碼模板如下:
// 二分搜索函數的定義里,除了要指定數組 nums 和目標查找數 target 之外,還要指定查找區間的起點和終點位置,分別用 low 和 high 去表示。
int binarySearch(int[] nums, int target, int low, int high) {
// 為了避免無限循環,先判斷,如果起點位置大于終點位置,表明這是一個非法的區間,已經嘗試了所有的搜索區間還是沒能找到結果,返回 -1。
if (low > high) {
return -1;
}
// 取正中間那個數的下標 middle。
int middle = low + (high - low) / 2;
// 判斷一下正中間的那個數是不是要找的目標數 target,是,就返回下標 middle。
if (nums[middle] == target) {
return middle;
}
// 如果發現目標數在左邊,就遞歸地從左半邊進行二分搜索。
if (target < nums[middle]) {
return binarySearch(nums, target, low, middle - 1);
} else {
return binarySearch(nums, target, middle + 1, high);
}//否則從右半邊遞歸地進行二分搜索。
}
注意:
- 在計算 middle 下標的時候,不能簡單地用 (low + hight) / 2,可能會導致溢出。
- 在取左半邊以及右半邊的區間時,左半邊是 [low, middle - 1],右半邊是[middle + 1, high],這是兩個閉區間。因為已經確定了 middle 那個點不是我們要找的,就沒有必要再把它加入到左、右半邊了。
- 對于一個長度為奇數的數組,例如:{1, 2, 3, 4, 5},按照 low + (high - low) / 2 來計算,middle 就是正中間的那個位置,對于一個長度為偶數的數組,例如 {1, 2, 3, 4},middle 就是正中間靠左邊的一個位置。
最后的時間復雜度是 O(logn)。
非遞歸解法
非遞歸寫法的代碼模板如下:
int binarySearch(int[] nums, int target, int low, int high) {
// 在 while 循環里,判斷搜索的區間范圍是否有效
while (low <= high) {
// 計算正中間的數的下標
int middle = low + (high - low) / 2;
// 判斷正中間的那個數是不是要找的目標數 target。如果是,就返回下標 middle
if (nums[middle] == target) {
return middle;
}
// 如果發現目標數在左邊,調整搜索區間的終點為 middle - 1;否則,調整搜索區間的起點為 middle + 1
if (target < nums[middle]) {
high = middle - 1;
} else {
low = middle + 1;
}
}
// 如果超出了搜索區間,表明無法找到目標數,返回 -1
return -1;
}為什么 while 循環的條件中是 <=,而不是 < ?
答:因為初始化 high 的賦值是nums.length - 1,即最后一個元素的索引,而不是 nums.length。
這二者可能出現在不同功能的二分查找中,區別是:前者相當于兩端都閉區間 [left, right],后者相當于左閉右開區間 [left, right),因為索引大小為 nums.length 是越界的。
我們這個算法中使用的是 [left, right] 兩端都閉的區間。這個區間就是每次進行搜索的區間。
實際應用
我們知道Kafka是一款性能強大且常用的分布式消息隊列,常常用于對流量進行消峰、解耦系統和異步處理部分邏輯以提高性能的場景。
在Kafka中,所有的消息都是以日志的形式存儲的。
你可以認為Kafka的海量消息就是按照寫入的時間順序,依次追加在許多日志文件中。
那在某個日志文件中,每條消息自然會距離第一條消息有一個對應的offset,不過這里的offset更像是一個消息的自增ID,而不是一個消息在文件中的偏移量。
Kafka的每個topic會有多個partition,每個partition下的日志,都按照順序分成一個個有序的日志段,順次排列。
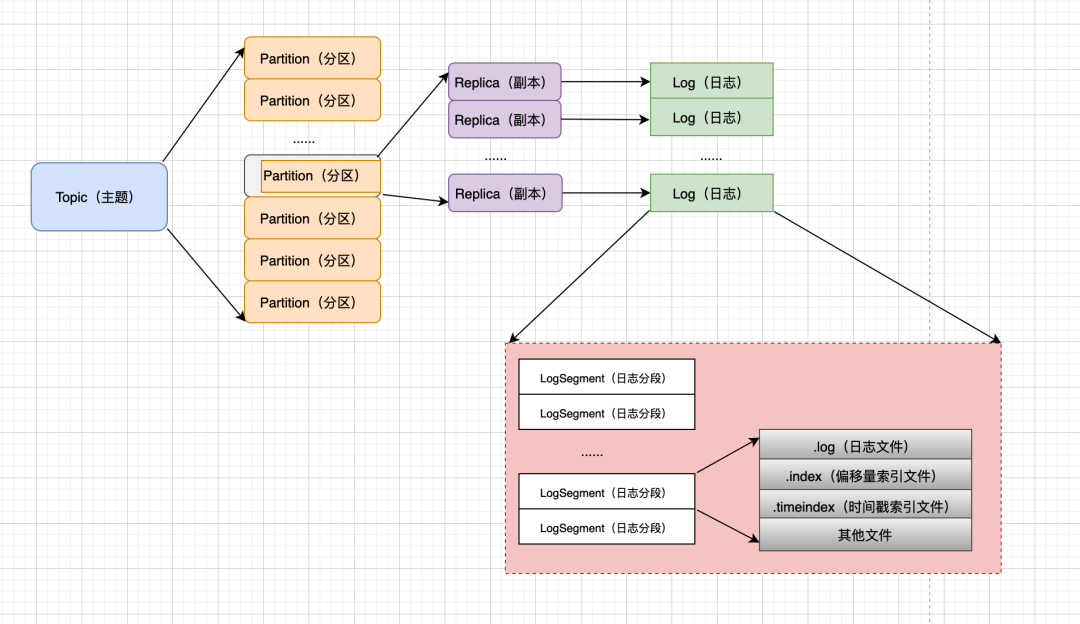
怎么找到消息
Kafka雖然不允許從尾部以外的地方插入或者修改數據,但我們在Kafka中還是很可能需要從某個時間點開始讀數據的,這就意味著我們要通過一個offset,快速查找到某條消息在日志文件的什么位置。
但由于每條消息的消息體不同,每條消息所占用的磁盤大小都是不同的,只有offset,沒有辦法直接定位到文件的位置。
所以我們要么遍歷日志文件進行查找,要么我們為日志文件建立一套索引系統,將消息offset和在文件中的position關聯起來,這樣我們就可以利用消息offset的有序性,通過二分法加速查找了。
下面是某個topic的某個partition下(日志文件)的存儲情況:
00000000000000000000.log
00000000000000000000.index
00000000000000000000.timeindex
00000000000000000035.log
00000000000000000035.index
00000000000000000035.timeindex
- .log文件就是存儲了消息體本身的日志文件;
- .index文件就是用于幫我們快速檢索消息在文件中位置的索引文件;
- 這里還有個.timeindex后綴的文件,它和index其實差不多都是索引文件,只不過在這個文件中關聯position的變成了時間戳。
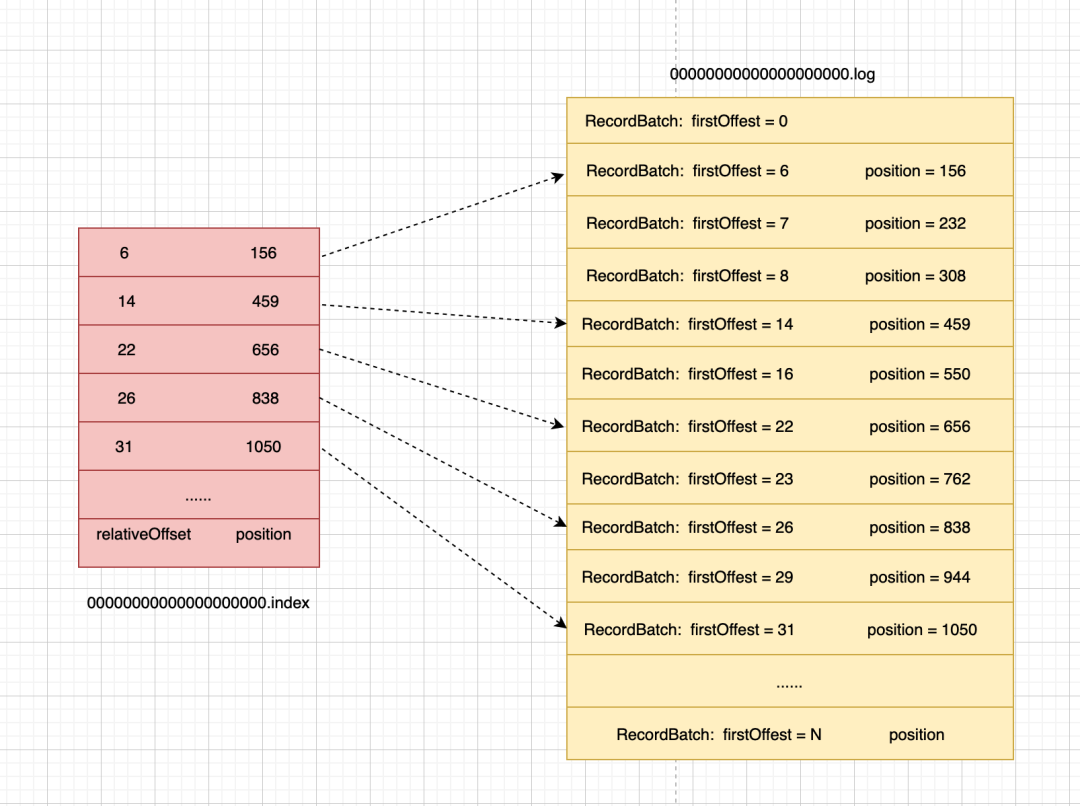
例題分析
找確定的邊界
邊界分上邊界和下邊界,有時候也被成為右邊界和左邊界。確定的邊界指邊界的數值等于要找的目標數。
例題:LeetCode 第 34 題,在一個排好序的數組中找出某個數第一次出現和最后一次出現的下標位置。
示例:輸入的數組是:{5, 7, 7, 8, 8, 10},目標數是 8,那么返回 {3, 4},其中 3 是 8 第一次出現的下標位置,4 是 8 最后一次出現的下標位置。
解題思路
在二分搜索里,把第一次出現的地方叫下邊界,把最后一次出現的地方叫上邊界。
那么成為 8 的下邊界的條件:
- 該數必須是 8;該數的左邊一個數必須不是 8;8 的左邊有數,那么該數必須小于 8;8 的左邊沒有數,即 8 是數組的第一個數。
成為 8 的上邊界的條件:
- 該數必須是 8;該數的右邊一個數必須不是 8:8 的右邊有數,那么該數必須大于8;8 的右邊沒有數,即 8 是數組的最后一個數。
代碼實現
用遞歸的方法來尋找下邊界,代碼如下:
int searchLowerBound(int[] nums, int target, int low, int high) {
if (low > high) {
return -1;
}
int middle = low + (high - low) / 2;
//判斷是否是下邊界時,先看看 middle 的數是否為 target,并判斷該數是否已為數組的第一個數,或者,它左邊的一個數是不是已經比它小,如果都滿足,即為下邊界。
if (nums[middle] == target && (middle == 0 || nums[middle - 1] < target)) {
return middle;
}
if (target <= nums[middle]) {
return searchLowerBound(nums, target, low, middle - 1);
} else {
return searchLowerBound(nums, target, middle + 1, high);
} //不滿足,如果這個數等于 target,那么就得往左邊繼續查找。
}查找上邊界的代碼如下:
int searchUpperBound(int[] nums, int target, int low, int high) {
if (low > high) {
return -1;
}
int middle = low + (high - low) / 2;
//判斷是否是上邊界時,先看看 middle 的數是否為 target,并判斷該數是否已為數組的最后一個數,或者,它右邊的數是不是比它大,如果都滿足,即為上邊界。
if (nums[middle] == target && (middle == nums.length - 1 || nums[middle + 1] > target)) {
return middle;
}
if (target < nums[middle]) {
return searchUpperBound(nums, target, low, middle - 1);
} else {
return searchUpperBound(nums, target, middle + 1, high);
} //不滿足時,需判斷搜索方向。
}找模糊的邊界
二分搜索可以用來查找一些模糊的邊界。模糊的邊界指,邊界的值并不等于目標的值,而是大于或者小于目標的值。
例題:從數組 {-2, 0, 1, 4, 7, 9, 10} 中找到第一個大于 6 的數。
解題思路
在一個排好序的數組里,判斷一個數是不是第一個大于 6 的數,只要它滿足如下的條件:
- 該數要大于 6;該數有可能是數組里的第一個數,或者它之前的一個數比 6 小。只要滿足了上面的條件就是第一個大于 6 的數。
代碼實現
Integer firstGreaterThan(int[] nums, int target, int low, int high) {
if (low > high) {
return null;
}
int middle = low + (high - low) / 2;
//判斷 middle 指向的數是否為第一個比 target 大的數時,須同時滿足兩個條件:middle 這個數必須大于 target;middle 要么是第一個數,要么它之前的數小于或者等于 target。
if (nums[middle] > target && (middle == 0 || nums[middle - 1] <= target)) {
return middle;
}
if (target < nums[middle]) {
return firstGreaterThan(nums, target, low, middle - 1);
} else {
return firstGreaterThan(nums, target, middle + 1, high);
}
}旋轉過的排序數組
二分搜索也能在經過旋轉了的排序數組中進行。
例題:LeetCode 第 33 題,給定一個經過旋轉了的排序數組,判斷一下某個數是否在里面。
示例:給定數組為 {4, 5, 6, 7, 0, 1, 2},target 等于 0,答案是 4,即 0 所在的位置下標是 4。
解題思路
對于這道題,輸入數組不是完整排好序,還能運用二分搜索嗎?
由于題目說數字了無重復,舉個例子:
1 2 3 4 5 6 7 可以大致分為兩類,
第一類 2 3 4 5 6 7 1 這種,也就是 nums[start] <= nums[mid]。此例子中就是 2 <= 5。
這種情況下,前半部分有序。因此如果 nums[start] <=target
第二類 6 7 1 2 3 4 5 這種,也就是 nums[start] > nums[mid]。此例子中就是 6 > 2。
這種情況下,后半部分有序。因此如果 nums[mid]
代碼實現
int binarySearch(int[] nums, int target, int low, int high) {
if (low > high) {
return -1;
} //判斷是否已超出了搜索范圍,是則返回-1。
int middle = low + (high - low) / 2; //取中位數。
if (nums[middle] == target) {
return middle;
} //判斷中位數是否為要找的數
if (nums[low] <= nums[middle]) { //判斷左半邊是不是排好序的。
if (nums[low] <= target && target < nums[middle]) { //是,則判斷目標值是否在左半邊。
return binarySearch(nums, target, low, middle - 1); //是,則在左半邊繼續進行二分搜索。
}
return binarySearch(nums, target, middle + 1, high); //否,在右半邊進行二分搜索。
} else {
if (nums[middle] < target && target <= nums[high]) { //若右半邊是排好序的那一半,判斷目標值是否在右邊。
return binarySearch(nums, target, middle + 1, high); //是,則在右半邊繼續進行二分搜索。
}
return binarySearch(nums, target, low, middle - 1); //否,在左半邊進行二分搜索。
}
}不定長的邊界
前面介紹的二分搜索的例題都給定了一個具體范圍或者區間,那么對于沒有給定明確區間的問題能不能運用二分搜索呢?
例題:有一段不知道具體長度的日志文件,里面記錄了每次登錄的時間戳,已知日志是按順序從頭到尾記錄的,沒有記錄日志的地方為空,求當前日志的長度。
解題思路
可以把這個問題看成是不知道長度的數組,數組從頭開始記錄都是時間戳,到了某個位置就成為了空:{2019-01-14, 2019-01-17, … , 2019-08-04, …. , null, null, null …}。
思路 1:順序遍歷該數組,一直遍歷下去,當發現第一個 null 的時候,就知道了日志的總數量。很顯然,這是很低效的辦法。
思路 2:借用二分搜索的思想,反著進行搜索。
- 一開始設置 low = 0,high = 1
- 只要 logs[high] 不為 null,high *= 2
- 當 logs[high] 為 null 的時候,可以在區間 [0, high] 進行普通的二分搜索
代碼實現:
// 先通過getUpperBound函數不斷地去試探在什么位置會出現空的日志。
int getUpperBound(String[] logs, int high) {
if (logs[high] == null) {
return high;
}
return getUpperBound(logs, high * 2);
}
// 再運用二分搜索的方法去尋找日志的長度。
int binarySearch(String[] logs, int low, int high) {
if (low > high) {
return -1;
}
int middle = low + (high - low) / 2;
if (logs[middle] == null && logs[middle - 1] != null) {
return middle;
}
if (logs[middle] == null) {
return binarySearch(logs, low, middle - 1);
} else {
return binarySearch(logs, middle + 1, high);
}
}`



































