4 月 20 日，在機器之心「量子計算」線上圓桌活動中，機器之心邀請到了中科院計算所研究員、量子計算實驗室主任孫曉明。他的演講主題為《量子搜索算法與線路優化》，報告簡要回顧了搜索算法和線路優化的發展以及目前面臨的挑戰，介紹了其團隊在這兩方面的一些工作進展。

演講回顧視頻（點擊閱讀原文查看）：https://app6ca5octe2206.pc.xiaoe-tech.com/detail/p_62612f69e4b09dda125e441b/6?fromH5=true

機器之心對他的演講內容做了不改變原意的編輯。我今天想要介紹的是關于量子搜索算法與線路優化，重點介紹搜索這部分。眾所周知，搜索是在經典計算機上面應用最廣泛的算法之一，它可以應用于搜索引擎、路徑導航或者推薦系統等。現在它還可以應用于新藥的研發，甚至我們可以將密碼破譯看成一個搜索問題。

舉例而言，我們想要破譯一個哈希函數，相當于要搜到一個字符串，使得它哈希之后滿足某一些特性，比如它的前 32 位都是 0，等等。我們知道，計算機算法界有一套被奉為圣經的圖書——Knuth 所著的《計算機編程的藝術》（The Art of Computer Programming），它的整個第三卷都在講 Sorting 和 Searching，由此可見搜索的重要性。

量子搜索算法

我們也知道，量子計算在 90 年代突然火了起來，其中一個重要的原因是兩個重要算法的提出，即 Shor 算法和 Grover 算法。Grover 算法Grover 算法可以在一個無序的數據庫上去查找一個特定的元素，比如想在一個數據庫里查一個特定的 IP 地址，或者找一個哈希函數的原像，以及棋類游戲的最優策略，都可以看作一個搜索任務。

對于經典算法來說，在一個沒有加過索引的數據庫上，如果數據庫的規模是 n 的話，那么肯定需要線性于 n 的時間。而量子算法可以有開平方量級的加速，它雖然沒有像 Shor 算法那樣能夠達到一個指數規模的加速，但開平方在很多情況下其實也很有意義。比如說在大數據處理中，本來有 1 億條的數據要處理，Grover 算法可以做到萬這個量級。再比如密碼分析，原本是 2 的 90 次方的一個暴力枚舉算法，我們可以降到 2 的 45 次方左右。對于現在的超算，2 的 45 次方的規模是可以接受的。

對于 Grover 搜索，它里面要用到一個很重要的模塊——Oracle。我們經常會看到這樣一種說法，如果有 50 個量子比特就可以實現 2 的 50 次方的并行加速，這件事情基本上是對的。他其實在說這樣一件事情，如果可以制備 n 個比特的疊加態，譬如我們記 n 是 logN 的話，那么事先制備 n 個零態，然后做一個 Hardmard 變換之后，它就可以生成所有的從 1 到 N（或者從 0 到 N-1=2 的 n 次方減 1）個計算基的疊加態。然后根據線性性，它經過一個 Oracle 之后就可以計算全部的 f(x)（x=1~N），會得到這樣一個態（圖中包含藍色的疊加態）。

這里其實有兩個問題，剩余的報告里也會談到，就是涉及到 Oracle 的制備，它是基于 QRAM 可以實現的角度。但在很多問題當中，這個 Oracle 是有具體的意義的，比如像我們剛才介紹過的，它可能是下圖左上角的一個哈希函數，或者甚至是一個 NP 完全問題，比如一個 SAT 公式等。這樣一個 oracle 該怎么制備呢？其實大家很早（例如 Nielsen 和 Chuang 的《Quantum Computation and Quantum Information》書中）就定性地知道：只要是一個可逆函數，那么都可以通過量子的方式實現出來。最近，我們在 oracle 的定量實現方面做過這樣一個工作，已經上傳到了 arxiv 上。我們針對的是這樣一類函數，即 CNF 或者 SAT oracle 的制備。論文地址：https://arxiv.org/pdf/2101.05430.pdf

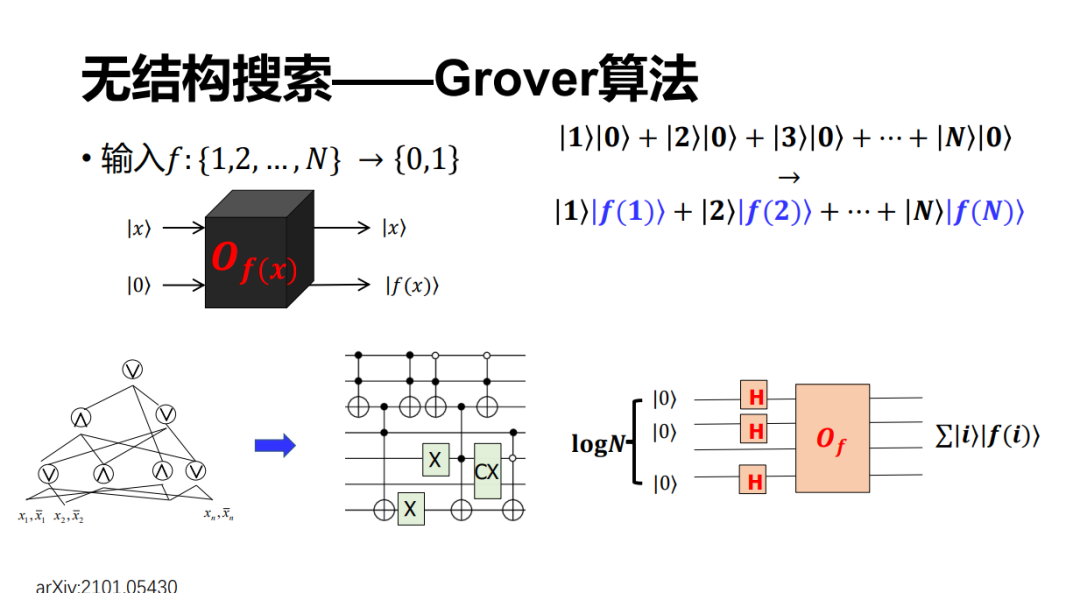
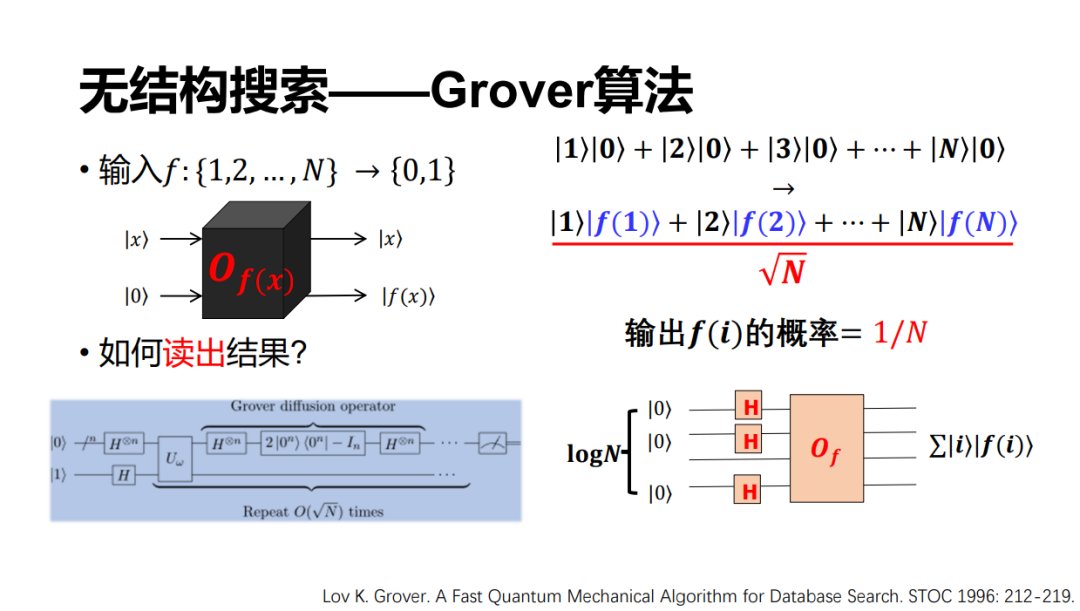
另外一個問題是怎么樣讀出計算結果？我們知道量子的測不準原理， 2^n個結果是不可能一次全部讀出來的，每次讀出來的概率其實只有1/2^n，這意味著如果有50個比特的話，每次只有 1/2^50 的概率看見任何一個結果。如果想要拿到特定的計算結果，又要花 2^50 的時間重復測量，所以這里量子就沒有產生加速。

但是，Grover 算法很巧妙的設計了一個通過若干次的對稱和反轉，然后只需要根號 N 的時間，就能夠以高概率拿到我們想要的結果。

振幅放大算法

在 Grover 之后，理論工作者又提出了一個被稱為振幅放大的算法，它想要解決的是這樣一個場景：如果現在有一個隨機搜索算法，它的成功率可能比較低，比如萬分之 1。我們希望通過調用這個算法來拿到一個高的成功概率。

古人常說，「三個臭皮匠頂個諸葛亮」。如果每一個算法的成功概率是萬分之 1，那么我們平均要重復 1 萬次。但是，使用振幅放大算法的思想（它和 Grover 很像）可以做到開平方，也就是說本來要 1 萬次，其實只需要大約 100 次這個量級就可以做成。

當然這需要事先把這個算法變成一個量子算法，然后才可以產生這樣一個加速。比如說我們把它應用到剛才說的 NP 完全問題或 SAT 問題上，如果隨機地選一個解，成功的概率是 1/2^n。所以，如果只是簡單粗暴地使用一下 Grover 算法，就可以做到根號 2 的 n 次方，也就 1.414^n。

但是還可以再加一些算法設計的技巧，這是因為剛才只是簡單地調用一下 Grover 算法，并沒有任何算法的技術在里面。假如做一些更好的算法設計，并使用一些更好的 SAT 求解算法的話，事實上復雜性可以做到比原來要小很多。

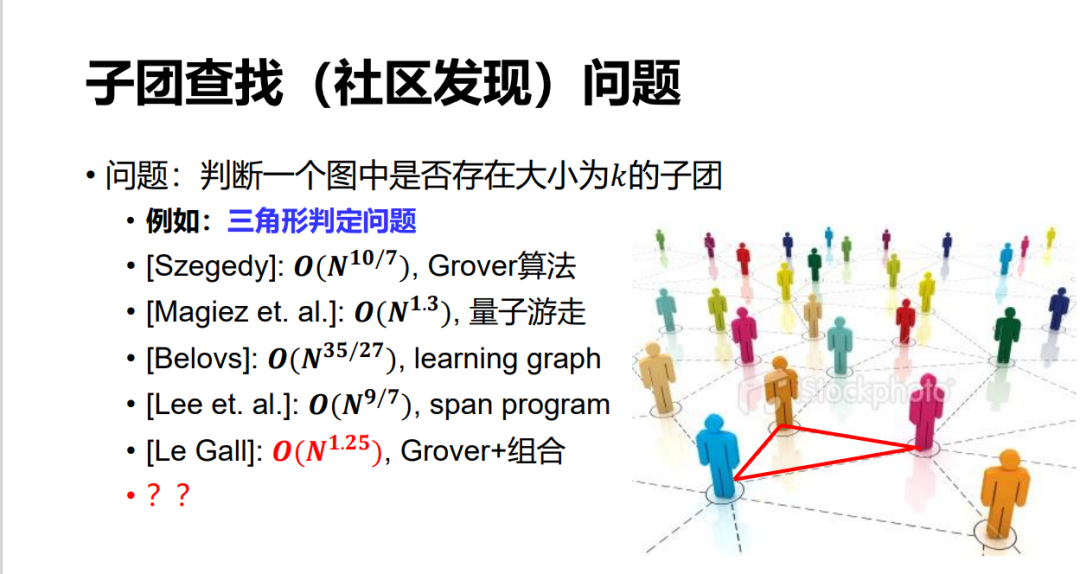
另外還有一些問題，比如在大數據里，我們經常想在一個社區里找一個子團，哪怕是找一個三角形這樣最簡單的子團。其實，這個問題到現在都不知道它最好的量子算法可以做到什么程度。

如果簡單地用 Grover 算法可以做一個 n^1.5 的算法，因為三角形一共最多是 n^3，所以 Grover 就可以做 n^1.5。后來 Szegedy 可以做到 n^10/7，到現在可以做到 n^5/4。但是否還有更好的，我們尚不清楚。

這其實給我們一個啟示，即很多人在問的量子算法為什么設計起來比較難。在我看來，一個方面的原因是量子確實有一點反直觀，它不像我們經典世界那樣看得見摸得著，所以設計起來是有不小的難度。另一方面目前從事該方向研究的人員還很不足，紐約時報的一個報道稱全世界從事量子計算的專家不超過一千人。

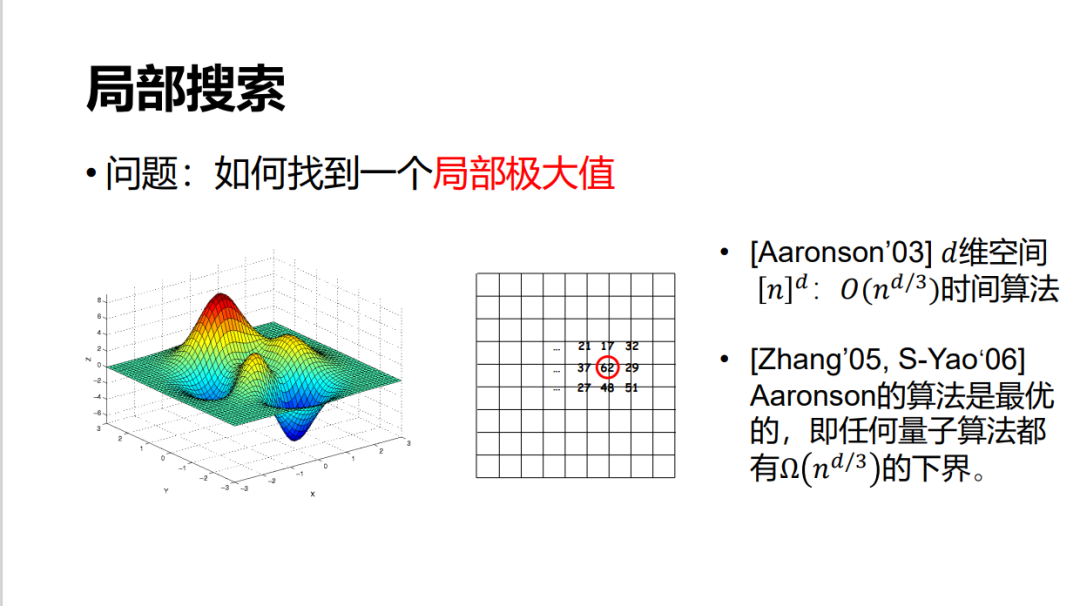
研究成果介紹局部搜索下面介紹我與勝譽以前共同做的一個工作：Grover 搜索可以用來解求全局極值，即需要根號 n 的時間就可以找到一個全局極大值或極小值。如果我們只需要找一個局部極值，譬如在機器學習里有很多應用，很多時候其實找一個局部極值就可以。Aaronson 最早研究了這一問題并給出了一個基本上可以做到開三次方的算法。勝譽、姚老師和我一起證明了，這個開三次方的加速就是最好的了。

權重判定

下面分享一下我們最近做的一個小工作，稱為權重判定問題。它需要區分這樣兩種情況，即解的個數或者有 k 個或者有 l 個，k 和 l 是事先給定的兩個數。其他的情形都不管，只需要能區分這兩種權重就行。

我們可以看到一些特例，譬如說 k 等于 0，l 等于 n/2，即恰好有一半解還是一個解都沒有。這個就是最早提出的第一個量子算法，即 Deustch-Josza 算法要做的事情。再譬如 k 等于 0，l 等于 1，區分有沒有至少一個解，這個就是 Grover 算法做的事情。

其實在我們之前，中山大學的邱道文老師他們做過一些工作，另外其他研究者也做過一些工作，這里不再一一贅述。

主要結果接下來直接說一下我們的結論，我們給出了一個下界和一個上界。這里我用圖來說明上下界分別是什么樣子。右上圖說的是上界，也就是一個量子算法。對于不同的參數 d，我們可以首先生成一批點，譬如之前的工作能做的區域只有綠色、紅色以及這些點（中間圖）。我們基本上把所有的區域都解決了，比如說 d=2 的時候有兩個點（右上圖），這兩個點它左上都只需要 1 次量子查詢，就和（左圖）綠色的一樣。

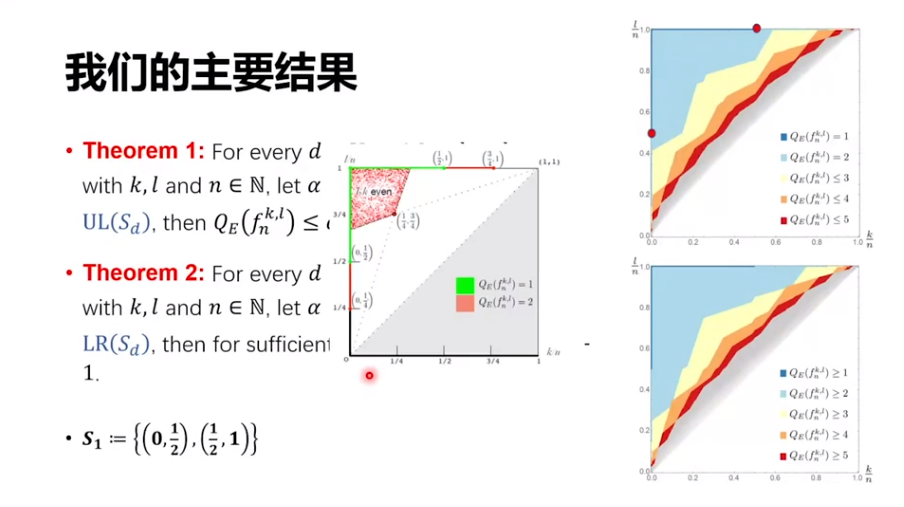
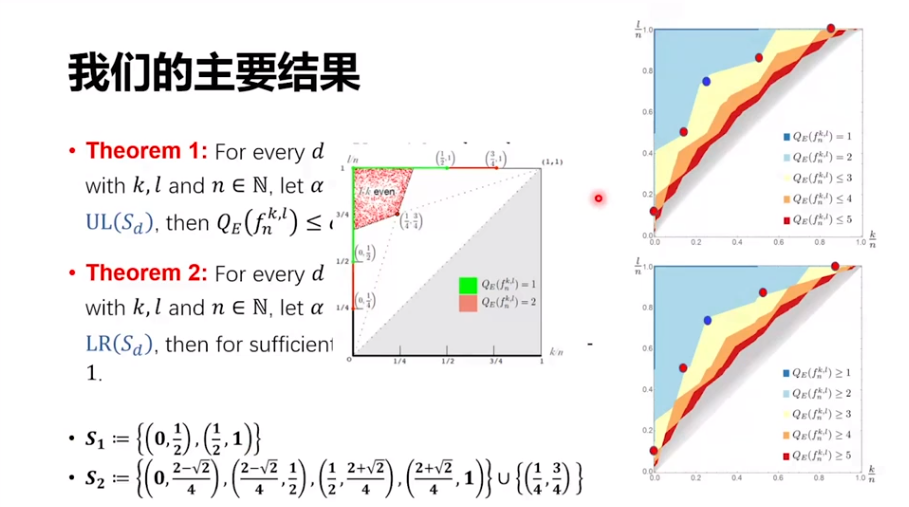
再下一個 Case 有 5 個點，就是下面右上圖中的 4 個紅點和 1 個藍點。它的左上方的淺藍色區域，量子只需要兩步就可以解決，完全覆蓋了之前的一些結論。同時，這 5 個點的右下方，也就是右下圖淺黃色這片區域。我們可以證明，它們是不可能用量子兩步解決的，至少要三步。然后，我們進一步定義集合 S_3，即有另一批點。它的左上方有一個算法可以 3 步做成，它的右下方任何算法至少要 4 步才能做成，類似可以推廣到任意的d。剛才勝譽的工作也提到了我以前的博士生袁佩，這個工作是和袁佩博士、現在的一個博士生何嘯宇以及前同事楊光一起做的。

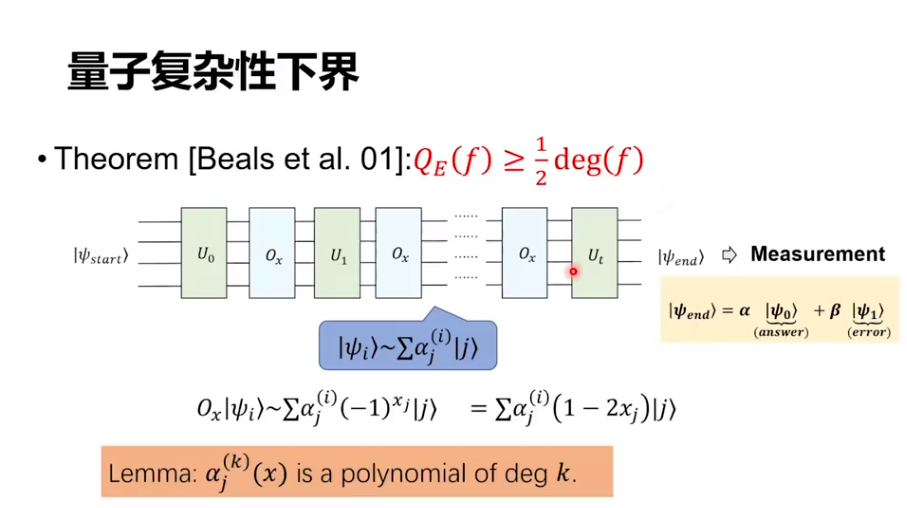
量子復雜性下界同時我們還做了一個下界，也就是說，我們可以證明在一些區域上量子不能做得特別好。其中最核心的一個定理是 2001 年 Beals 等人證明的一個結論，對精確量子算法，它的復雜度可以被這個函數寫成一個多項式后它的 Degree 除以 2 給出一個下界。所以，我們就可以把這個問題轉化成去考慮它的多項式表示的多項式次數。

研究多項式次數需要用到一些工具，這里有一個很著名的多項式叫切比雪夫多項式（Chebyshev Polynomials），就是說 cos mθ（m 是一個整數）都可以寫成 cos θ的一個多項式，比如根據二倍角公式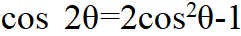，cos 3θ可以寫成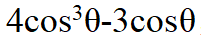，等等。

Grover 搜索背后的關鍵其實也是這樣一個切比雪夫多項式。我們在這個工作中也要用到它，最關鍵的一點就是切比雪夫多項式構成了多項式空間的一組基。接著我們把任何一個多項式展開到這組基上，再利用切比雪夫多項式的一些性質證出來一個下界。

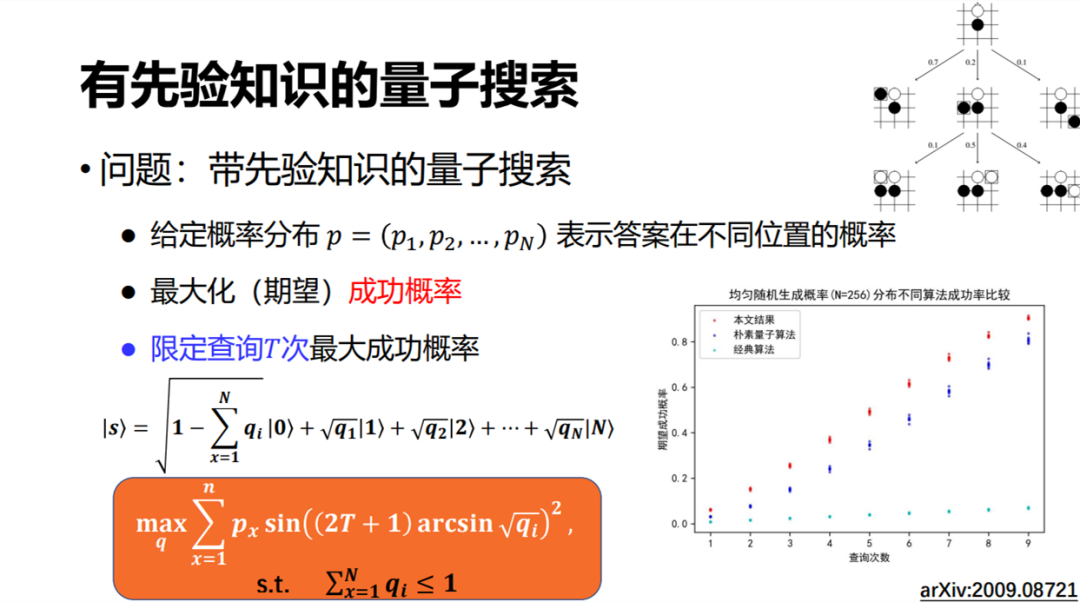
帶先驗知識的量子搜索下面介紹我們最近做的另一個工作，稱為帶先驗知識的量子搜索。由于在 Grover 搜索中，我們對想要找的解一無所知，也就是說它是任何一個的概率都是相等的。但在有些搜索問題里，比如α-β剪枝，我們事先知道一定的概率分布，即走哪條路的概率更高一點。

假如我們現在把它建模成 p = (p_1, p_2, …, p_N) 的形式，我們知道 1 是解的概率是 p_1，2 是解的概率是 p_2，N 是解的概率是 p_N。在這種情況下怎樣做一個最好的搜索呢？我們最近研究了這個問題，大概的核心結論是需要制備一個特殊的初態，這也是后來我們跟勝譽一起討論初態制備問題的出發點之一。制備了這個特殊的初態之后，后面的算法步驟（對稱、翻轉等）跟 Grover 算法很像。我們可以證明，這樣做在漸進意義上幾乎是最優的。

電路優化下面再簡單介紹一下量子電路優化方面的工作。最近，量子硬件發展很快，John Preskill 教授在 2018 年提出了一個概念，叫做 NISQ（含噪聲、中等尺度量子系統）。剛才勝譽也提到 IBM 有個路線圖，稱明年就可以做到 1000 多個比特。但是，它的特點是噪聲很大，所以需要壓縮電路的深度。

之前我們做了這樣一個工作，就是去討論 CNOT 電路的線路深度。眾所周知，CNOT 加上單比特門就是 Universal 的，可以生成任何的量子電路。所以，CNOT 電路有一定的重要性。

下面是一個例子，說明一個 CNOT 電路可以轉成一個等價的電路。原來的深度是 7，現在深度是 5。最核心的一點是，CNOT 電路本質上可以寫成這些變量的一個線性組合。

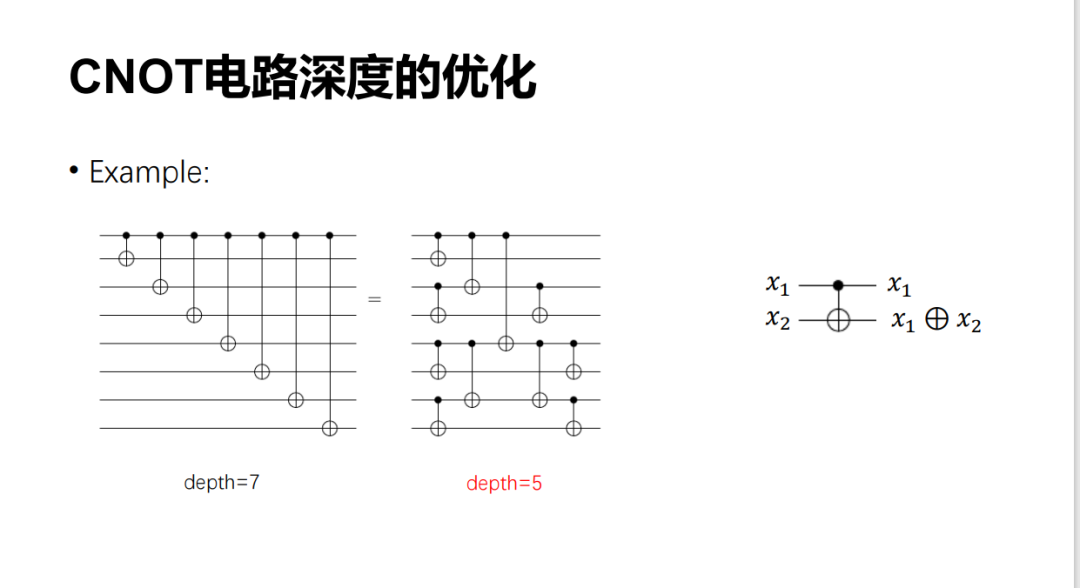
CNOT 電路的化簡其實和 F_2 上的可逆矩陣分解有重要聯系。事實上，我們在每一層上可以放多個 CNOT 門，譬如下面左下圖第一層放了兩個 CNOT 門，它對應右下圖第二個矩陣。從線性代數上，可以將它看作一個行消元，即把第一行加到第二行，第三行加到第四行。

所以，CNOT 電路的化簡可以變成這樣一個數學問題，即如果允許并行的高斯消元，要把一個可逆的矩陣化成單位陣，最少需要多少步？注意每一步可以并行地來做。

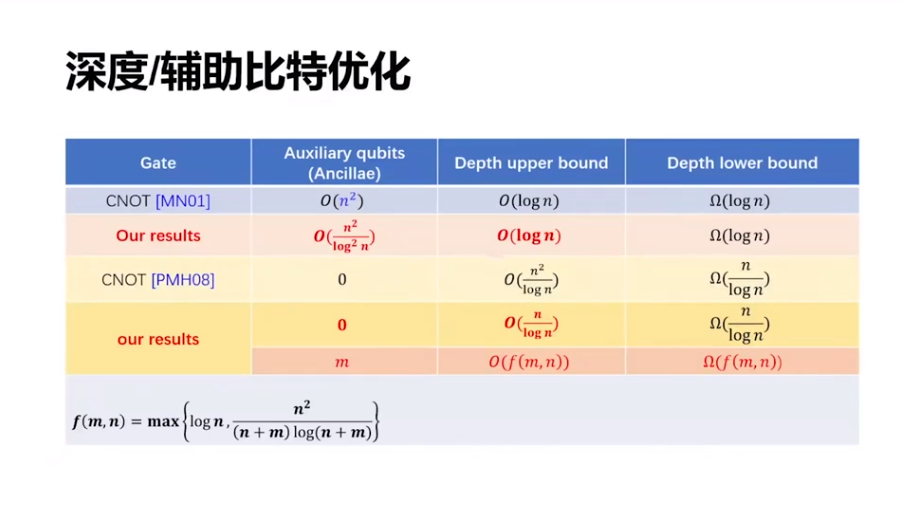
結果介紹我們做了如下一些結果，主線是討論輔助比特和電路深度之間的關系。這是之前的結果，輔助比特達到 n^2 的時候有一個結果，輔助比特為 0 的時候也有一些結果。我們可以把兩邊的結果都加以改進，而且還有一個更一般性的結果，就是如果有 m 個輔助比特，那么這個電路深度可以優化到一個緊的界，即下圖右下方的表達式。特別的當 m 等于 0 和 m 等于 n^2 的時候，我們的結果分別可以把原來的兩個界優化一些。

團隊及書籍介紹下圖中是我們中科院計算所量子計算與算法理論實驗室團隊的一部分成員，包括剛才工作中提到的張家琳老師、田國敬老師、袁佩博士、蔣佳卿、何嘯宇和楊帥等。

這次活動我們得到了兩家出版社的大力支持。與尚云教授、李綠周教授、尹璋琦教授、魏朝暉博士、田國敬博士一起，我們花了三年時間翻譯了量子計算領域最經典的一本教材，即 Michael A. Nielsen 和 Isaac L. Chuang 合著的《量子計算與量子信息》（10 周年版）（Quantum Computation and Quantum Information 10th Anniversary Edition） ，譯著共 570 多頁。我們覺得它是一本非常優秀的教材，即使從現在的角度來看。當然，這本書確實缺少一些比較近期的（比如在硬件實現方面）內容。但是它作為入門教材對讀者非常友好，特別是如果你從屬于計算機領域，并且想要學習量子計算，那么你只需要掌握最基本的線性代數知識，閱讀這本書就完全沒有問題。