OpenHarmony啃論文俱樂部—數據高通量無損壓縮方案

【本期看點】
- ndzip應用場景
- ndzip相關算法
- 殘差編碼復現
- SIMD
【技術DNA】
【智慧場景】
********** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ******************** | ***************** |
場景 | 自動駕駛 / AR | 語音信號 | 流視頻 | GPU 渲染 | 科學、云計算 | 內存縮減 | 科學應用 | 醫學圖像 | 數據庫服務器 | 人工智能圖像 | 文本傳輸 | GAN媒體壓縮 | 圖像壓縮 | 文件同步 | 數據庫系統 |
技術 | 點云壓縮 | ?稀疏快速傅里葉變換? | 有損視頻壓縮 | 網格壓縮 | 動態選擇壓縮算法框架 | 無損壓縮 | 分層數據壓縮 | 醫學圖像壓縮 | 無損通用壓縮 | 人工智能圖像壓縮 | 短字符串壓縮 | GAN 壓縮的在線多粒度蒸餾 | 圖像壓縮 | 文件傳輸壓縮 | 快速隨機訪問字符串壓縮 |
開源項目 | ??SFFT?? | ??Ares?? | ??LZ4?? | ??DICOM?? | ??Brotli?? | ??RAISR?? | ??AIMCS?? | ??OMGD?? | ??rsync?? | ??FSST?? |
NDZIP — 一個用于科學數據的高通量并行無損壓縮器
概述
場景應用
- 分布式計算以及高性能計算在機器學習、大數據學習與高級建模與模擬等新興技術上都有使用。在航天航空、制造業、金融、醫療等多個領域也有著非常重要的作用。
- ndzip,是一種新的高吞吐量無損壓縮算法,專門為浮點數據的n維網格而設計,為HPC互連帶寬的的限制因素提供了一種有效的解決方案。
本文貢獻
- 本文提出了一種新的壓縮算法-ndzip,它基于一個快速,且并行整數近似的的知名預測器,并結合了對硬件友好的塊細分方案;
- ndzip 的高性能多級并行實現,利用SIMD? 和線程級并行;
- 對大量具有代表性的HPC 數據進行深入的性能評估,并與最新水平的專業浮點壓縮器和通用壓縮方案進行比較。
技術背景
相關算法
FPZIP
- FPZIP? 使用洛倫茲預測器利用標量 n 維網格內點的直接鄰域的平滑性,使用范圍編碼器壓縮小的殘值。該方案具有很高的壓縮效率,特別是對于單精度值。
FPC
- FPC? 使用一對基于哈希表?的值預測器來壓縮非結構化雙精度數據流。它提供了一個可調參數,利用壓縮效率提高速度。線程并行的pFPC 變體允許通過以塊的形式處理輸入數據來進一步確定壓縮吞吐量的優先級。
SPDP
- SPDP? 結合了一維預測和LZ77變體,可以壓縮單精度和雙精度數據,而不需要對任何一種格式進行專門處理。
MPC
- MPC? 是一種用于GPU 的快速壓縮方案。將一個簡單的一維值預測器與一個位重組方案相結合,可以很好地映射到目標硬件的殘差中去零位。
APE 和 ACE
- APE? 和ACE ?壓縮器自適應地從多個值預測器中選擇,將 n 維網格中的數據點與其已處理過的鄰居解相關。殘差使用一種變體的Golomb 編碼進行壓縮。
數值預測
數值預測科學浮點數據中的單個數值通常在低階尾數位表現出較高的熵,尾數也很少出現精確到重復,這降低了傳統字典編碼器的效率。相反,我們可以使用專門的方法對已經處理過的數據進行預測,只對殘差進行編碼。
- SPDP? 和MPC 使用簡單的固定步長值預測器,通過存儲 k 個值,并用最近編碼的第 k 個值預測每個點。
- FPC? 和pFPC 使用一對基于哈希表的預測器來維護一個較大的內部狀態,以利用值和值增量中的重復模式。
- fpzip? 使用浮點洛倫茲預測器來估計 n 維空間中長度為 2 的超立方體的一個角的值。fpzip通過奇數條邊可到達的所有其他角加起來,然后減去通過偶數條邊可到達的角。當超立方體可用n - 1次隱式多項式表達時,預測精度是精確的。
- APE 和 ACE 擴展了fpzip預測器的思想,通過在每個維度上使用高維多項式,以更大的計算成本為代價提高了預測精度。
差分運算
在無損壓縮環境中,浮點減法不適合用來計算預測殘差。小幅度的浮點值通常不會以簡短的、可壓縮的位的形式出現,而且浮點數的有限精度使浮點減法成為一種非雙射的運算。因此,所有研究的算法都明確地計算位表示的殘差。
- FPC和pFPC 使用逐位異或差?,而SPDP和MPC 將操作數位重新解釋為整數,并對整數減法的結果進行編碼。
- APE和ACE 提供了兩種變體。
- fpzip 也使用整數減法,但是它根據符號位對操作數進行反運算,以提高映射的連續性。
殘差編碼
精確的預測會產生具有許多相同前導位的小幅度殘差,即異或運算符為零以及二進制補碼的整數減法的冗余符號位。對這些前導位進行有效編碼是大多數研究方案中所采用的數據簡化機制。
- fpzip 使用一個范圍編碼器?來壓縮前導冗余位的數量,緊接著復制剩余位。距離編碼器能夠產生的接近最佳的位串使得其非常節省空間。然而,所需的位粒度尋址難的問題難以有效解決。
- APE? 和ACE? 使用與fpzip?類似的方法,但使用符號排序的Golomb 代碼來編碼冗余位的數量。
- FPC 和 pFPC 通過計算雙精度殘差中前導零字節的數量,使用固定映射對運行長度和4 bit中的預測部分進行編碼。剩余部分將從第一個非零字節開始逐字輸出。這種方法是無狀態的,在不可壓縮的情況下有可接受的1/16開銷,代價是由于粒度較低而浪費比特。
- MPC 將剩余流分成 32 個單精度(或 64 個雙精度)值的塊,發出 32(64)個最高有效位,然后是 32(64)個第二最高有效位,依此類推。零字將從輸出流中刪除,并在每個編碼所有非零字位置的塊上替換為32或64位掩碼。這種方法在不可壓縮的情況下有非常低的開銷,僅僅為1/32(1/64),由于字符粒度尋址,該方法在 GPU 上得到了有效的實現,但需要塊內所有的殘差具有相似的位寬才能實現。
- SPDP 從一個類似于 MPC 的重組策略開始,但是SPDP是在字節級別上的重組策略。SPDP接著使用字節粒度整數減差運算,并使用 lz77 系列編碼器對結果流進行編碼。這可以消除除前導零之外的重復模式,并使 SPDP 也能處理非浮點數據。
算法分析
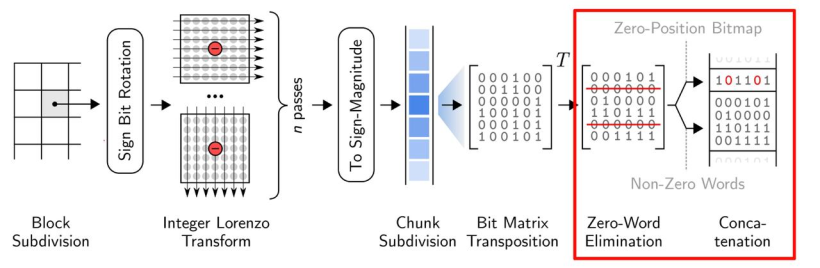
- ndzip 的算法主要分為塊細分、整數洛倫茲變換以及殘差編碼三個部分。
- 大體流程:下圖展示了ndzip壓縮管道的所有步驟,首先它將輸入的數據劃分為固定大小的超立方體,并使用多維變換在塊內對數據進行去相關,從而使其具有更短位表示殘差。然后通過位矩陣變換消除公共零位來壓縮剩余流。壓縮后的數據塊存儲在報頭旁邊,報頭顯示了輸出流中壓縮數據塊的位置。
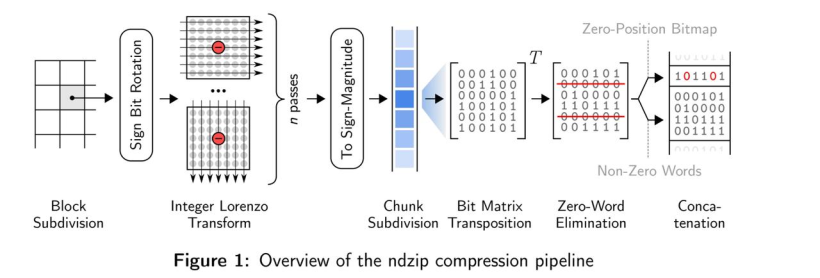
塊細分
- ndzip 不是一次性處理輸入數據的整個 n 維網格,而是將其細分為獨立壓縮的小的超立方體,然后依次進行傳輸。
- 由于該算法需要多次傳遞數據,因此可以更好地使用處理器緩存,但會略微損失解相關的效率。塊與塊之間存在依賴,我們想要消除塊之間的所有依賴關系,可以通過附加額外的數據來實現。
- 這里作者選擇了4096個元素,則超立方體的大小可以表示為40961、642或163。對于單精度,這相當于16KB的內存;對于雙精度,這相當于32KB的內存。預先確定塊的大小能夠在之后的步驟生成高度優化的機器碼。
- 當網格范圍不是塊的大小的倍數時,邊框元素將不被壓縮地附加到輸出中。
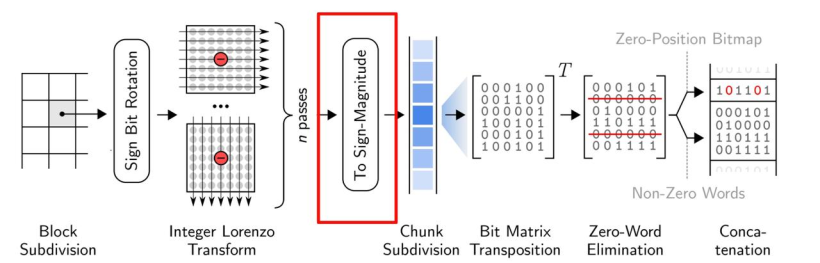
整數洛倫茲變換
浮點洛倫茲預測器(Floating-point Lorenzo Predictor) 對于多維數據的預測是非常高效的,但是單獨位模式的殘差計算需要解碼器從已經解碼的臨近值重建每個預測,從而引入限制并行計算的依賴。
因此,作者使用了整數洛倫茲變換( Integer Lorenzo Transform) 解決了這個問題。整數洛倫茲變換是一種直接計算整數域內的洛倫茲預測殘差的近似的多道運算。下圖便說明了這個過程。


殘差編碼
- 關于殘差編碼,ndzip使用了與 MPC 相同的殘差編碼方案,使其可以在現在的CPU上高效的實現。大致流程如下:
殘差使用了二進制補碼進行表示,根據殘差的符號,確定了補碼第一位是1還是0。之后通過0消去對兩者進行編碼。
殘差首先被轉換成符號-數值(sign-magnitude)表示,只要殘差為負,就對除了第一個比特外的所有比特進行翻轉。
然后將殘差流分成32個單精度或者64個雙精度的值,對每個塊進行 32x32(64x64) 的位矩陣變換
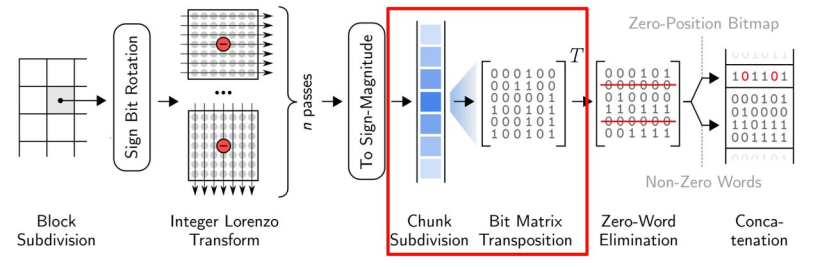
將來自相同位置的比特分組成單詞,從輸出中消去可以消去的0詞
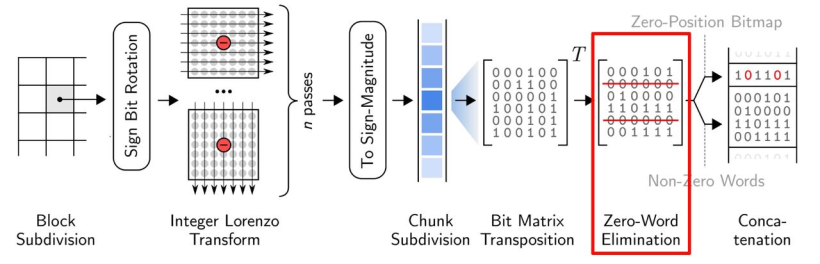
在每個塊前面加上一個32位(64位)的頭,將非0字的位置編碼為位圖。
使用教程
- 上面的原理看的有點頭禿,下面講解如何快速上手ndzip。
- 點擊進入 ndzip 的地址,git 下項目到本地。
環境搭建
環境需求
運行 ndzip 需要以下環境,Catch2 可根據自己是否需要來選擇是否安裝。
- CMake >= 3.15
- Clang >= 10.0.0
- Linux (我這里用的Ubuntu20)
- Boost >= 1.66
- Catch2 >= 2.13.3 (可選,用于單元測試和微基準測試)
CMake安裝
- CMake? 在Ubuntu軟件源中,安裝非常簡單,執行以下命令即可:
sudo apt install cmake
- 版本檢查(CMake >= 3.1.5):
cmake --version
- 看到 CMake 版本大于3.1.5?即可。

Clang 安裝
- Clang 也存在 Ubuntu軟件源中,步驟和CMake差不多,命令如下:
sudo apt install clang
- 版本檢查(Clang >= 10.0.0):
clang --version
- 可以看到 Clang 版本為10.0.0?,符合要求

Boost 安裝
- Boostr 也存在 Ubuntu軟件源中,命令如下:
```undefi`ned
sudo apt-get install libboost-all-dev
- 版本檢查(Boost >= 1.66):
```undefined
dpkg -S /usr/include/boost/version.hpp

Catch2 添加
- Catch2需要去github上下載編譯,命令如下:
git clone https://github.com/catchorg/Catch2.git
cd Catch2
cmake -Bbuild -H. -DBUILD_TESTING=OFF
sudo cmake --build build/ --target install
- 等待編譯添加完即可。
構建
使用 CUDA + NVCC 構建 ndzip
- 使用 cuda,安裝CUDA Toolkit:
sudo apt-key del 7fa2af80 # 刪除舊的GPG密鑰,之前裝過的要刪掉
wget https://developer.download.nvidia.com/compute/cuda/repos/wsl-ubuntu/x86_64/cuda-wsl-ubuntu.pin
sudo mv cuda-wsl-ubuntu.pin /etc/apt/preferences.d/cuda-repository-pin-600
wget https://developer.download.nvidia.com/compute/cuda/11.7.0/local_installers/cuda-repo-wsl-ubuntu-11-7-local_11.7.0-1_amd64.deb
sudo dpkg -i cuda-repo-wsl-ubuntu-11-7-local_11.7.0-1_amd64.deb
sudo apt-get update
sudo apt-get -y install cuda
- 使用CUDA + NVCC 構建 ndzip(自己使用SYCL構建ndzip沒跑出來。。。)
cmake -B build -DCMAKE_CUDA_ARCHITECTURES=75 -DCMAKE_BUILD_TYPE=Release -DCMAKE_CXX_FLAGS="-march=native"
cmake --build build -j
- 完成構建

測試
- 測試命令
- 測試ndzip壓縮

評價
解耦多維數據
- ndzip-gpu 通過變換在解耦多維數據時實現了高資源利用率。提出了一種用于垂直位打包的新穎、高效的曲速協同原語,提供了高吞吐量的數據縮減和擴展步驟, 為檢查的數據提供了最佳的平均壓縮比, 同時在雙精度情況下的數據減少和吞吐量之間保持了有利的權衡。將數據集的壓縮比定義為壓縮大小除以未壓縮大小(以字節為單位),比率越低表示壓縮越強。在需要匯總比率的情況下,返回數據集上壓縮比率的未加權算術平均值。
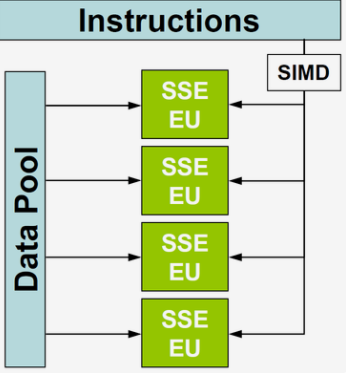
SIMD
- SIMD(Single Instruction Multiple Data),單指令多數據流,能夠復制多個操作數 ,并把它們打包在大型寄存器的一組指令集。
- ndzip專為在支持 SIMD 的現代多核處理器上高效實施而量身定制,能夠以接近主內存帶寬的速度壓縮和解壓縮數據,顯著優于現有方案。通過測量從系統內存壓縮和解壓縮到系統內存的時鐘時間來評估性能。第三方實現允許在必要時進行內存操作。返回每秒未壓縮字節的吞吐量,它轉換為壓縮輸入和解壓輸出帶寬。重復測量每個算法和數據集對,直到總運行時間超過一秒。在每次迭代之前,從 CPU 緩存中刪除輸入數據。
利用多維度的好處可以通過使用等效的一維變換來轉換高維數據集來衡量。
實驗
新型整數洛倫佐變換(ILT)的有效性
- 為了估計新型整數洛倫佐變換(ILT)的有效性,我們用其他預測方法代替了實現中的變換步驟,并比較了得到的壓縮比,通過使用等效的一維變換來轉換高維數據集來衡量。
- 如圖顯示了具有相同維度的所有數據集的平均壓縮比,相對于在各自維度中觀察到的最差壓縮比進行了縮放。
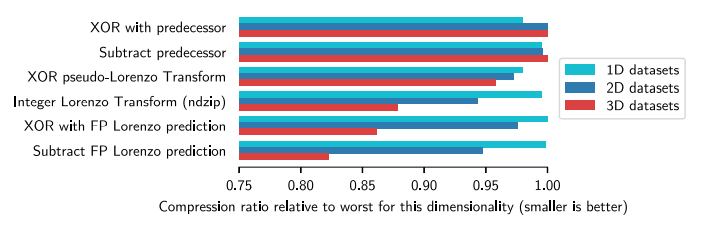
- 因為該維度相對最差的壓縮比(越小越好),對于一維數據集,所有方案大致相同。總體上看,FLP最好,最差的選擇是兩個一維預測器,這表明基于洛倫佐的組件顯著受益于更高的維度,選擇余數運算對于逼近 FLP 的相關特征至關重要。
算術平均未壓縮吞吐量 - 在測試數據上比較通過檢查的壓縮器實現,實現的吞吐量和壓縮比。 根據設計,同時并非所有算法都能同時處理單精度值和雙精度值。有些算法有一個或多個可調參數體現為連續的線,而ndzip,沒有可調的行為。
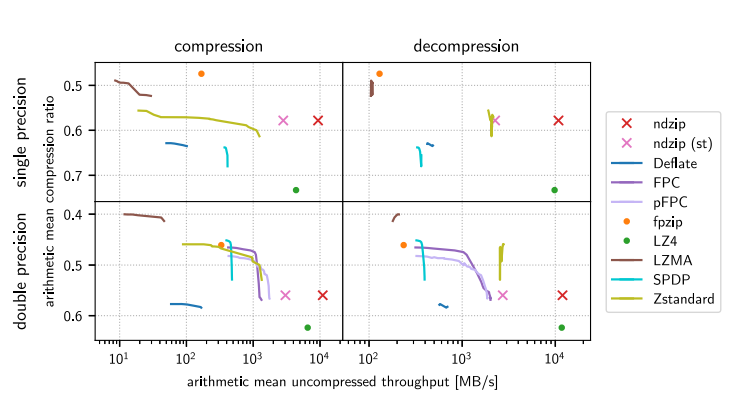
- 通用算法可以在浮點數據上實現高壓縮比,但只能以犧牲大量計算資源為代價。比如,LZMA 在雙精度值上實現了最高的壓縮比,與最強的單精度壓縮器 fpzip 不相上下,同時花費更多壓縮我們最大的數據集。LZ4 實現了比任何其他審查過的單線程算法更高的壓縮和解壓縮吞吐量,同時還提供了最差的數據縮減。Zstandard 提供了一個非常好的權衡,在單精度數據上主導 Deflate 和專門的 SPDP。大多數專業算法能夠在至少一個維度上勝過通用方案。而Fpzip 是最強大的單精度壓縮器,而且僅以中等吞吐量為代價,但在解壓縮方面失去了吞吐量比較.
- 所以ndzip 是最快的專用壓縮器和解壓縮器,具有顯著優勢(“st”)。 對于雙精度數據集,稍差一些。與一些速度較慢的算法相比,我們的壓縮器提供了更低的壓縮比,但在吞吐量方面明顯優于它唯一的競爭對手 LZ4。
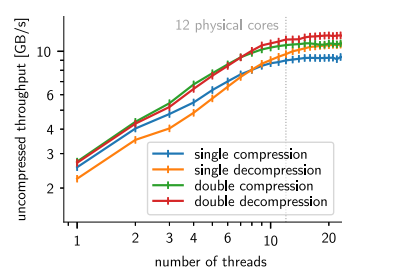
結論
- 通過設計一種考慮到目標架構特性的專用壓縮算法,可以實現出色的資源使用以及壓縮率和吞吐量之間極具競爭力的折中。基于我們新穎的小超立方體數據,利用了行整數洛倫佐變換(Integer Lorenzo Transform)和硬件友好的殘差編碼方案,ndzip 壓縮器利用 SIMD 和線程并行性在消費類硬件上實現超過 10 GB/s 的壓縮和解壓縮速度,顯著地減少數據量。












































