介紹

讓我們以一個例子來說明我們所面臨的問題。想象一下，我們訓練一個神經網絡模型來預測包含汽車圖像的概率。當我們使用這些概率來對有汽車的圖像進行分類時，我們的模型有很好的準確性。在某些時候，我們給神經網絡模型一個它從未見過的圖像，例如企鵝。該模型表示，圖像包含一輛汽車的概率為97%。基于這個例子，你會相信模型的預測嗎?事實證明，這是神經網絡的典型行為，因為企鵝與我們的訓練數據相差太大。這種知道未知對象的能力是我們要尋找的，因為它在一些決策應用中是至關重要的，比如自動駕駛汽車。

什么是模型不確定性？

當我們談論機器學習模型時，有兩種類型的不確定性：

• 隨機不確定性:它來自于數據生成過程中的隨機性，例如，實驗中的測量噪聲。不管我們的模型有多好，這種不確定性都無法減少。
• 認知不確定性：它來自于知識的缺乏，這在機器學習中意味著要么我們沒有足夠的數據，要么我們的模型不夠專業。如果我們獲得了新知識，這種不確定性可以減少。

考慮到這一點，讓我們看一下高斯過程給出的不確定性估計的具體例子。

高斯過程回歸

高斯過程(GP)是貝葉斯機器學習模型。這意味著對于一個給定的數據輸入點，我們將得到一個預測分布，而不是像我們在神經網絡中得到的點估計。預測方差可以解釋為不確定性的估計。

但是，這些模型是如何工作的呢?讓我們想象我們有以下回歸問題

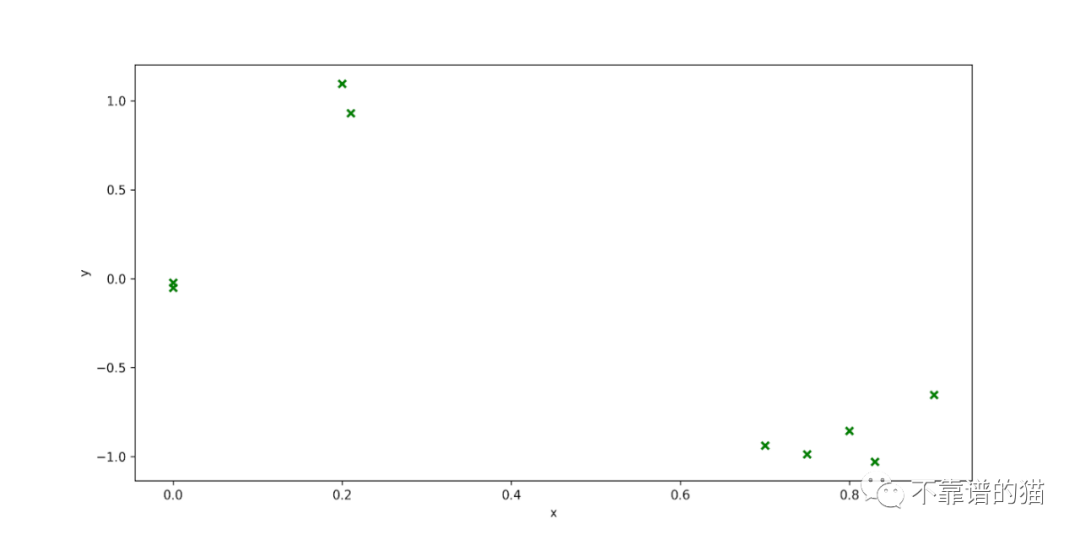
要解決的問題是找到更適合數據的函數。為此，我們假設觀測y是產生數據的函數的噪聲觀測。也就是說,

y=f(x)+?

其中， ? ～ ??(0, σ2)是加性高斯噪聲，方差σ2對應于任意不確定性。

對于GP模型，我們假設生成數據的函數可以從高斯過程中得到，它可以被視為函數的分布。我們可以用均值函數m(x)和協方差函數k(x,x)來描述GP，即:

GP(m(x),k(x,x))

在實踐中，我們在函數p(f) ~??(0,k(x, x)) 上放置了一個 GP 先驗，其中將均值函數設置為0以簡化所需的計算而不損失通用性是一種常見的做法。這使得GP完全由其協方差函數或核來表征。核函數的選擇將決定學習的函數的主要屬性(平滑性、平穩性等)。常見的核選擇是徑向基函數或RBF核，它假定函數是平穩的。

如果我們使用貝葉斯規則將這些先驗知識與觀察到的數據結合起來，我們將獲得函數值的后驗分布。

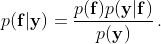
分母中有一個有趣的項，稱為邊際似然(marginal likelihood)或模型證據(model's evidence)，它是一個歸一化常數，可用于訓練模型和尋找核函數的最佳參數。我們會得到滿足給定屬性并與數據兼容的函數。

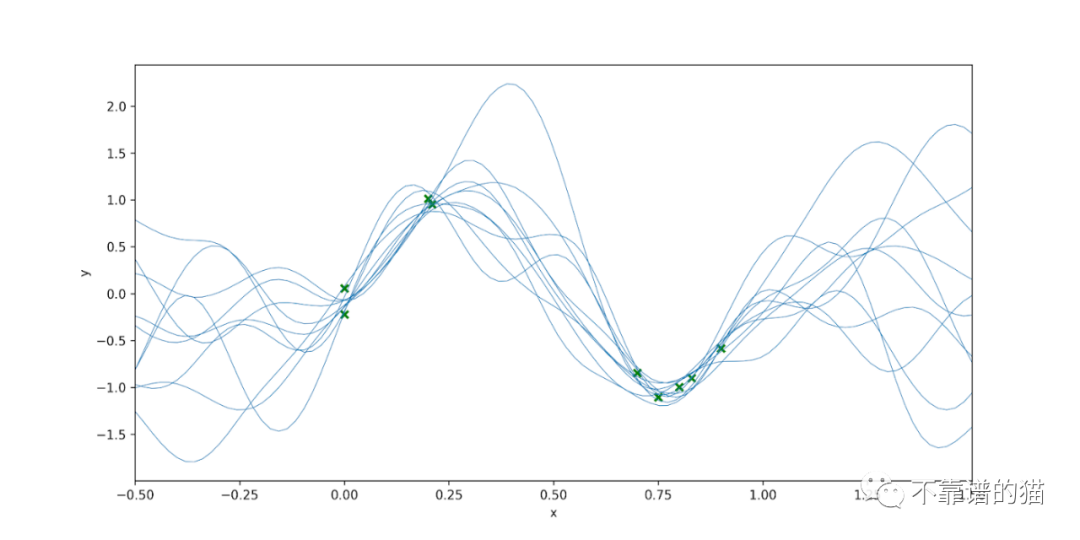
注意，在我們沒有觀察數據的區域，函數的可變性比我們有數據點的區域要高。有趣的是，我們可以利用這個后驗得到一個預測分布來進行預測和相關的不確定性估計，最重要的是，這個分布可以以封閉形式計算。這里不會詳細介紹，但它是均值和方差的高斯分布。這個問題的預測分布如下所示:

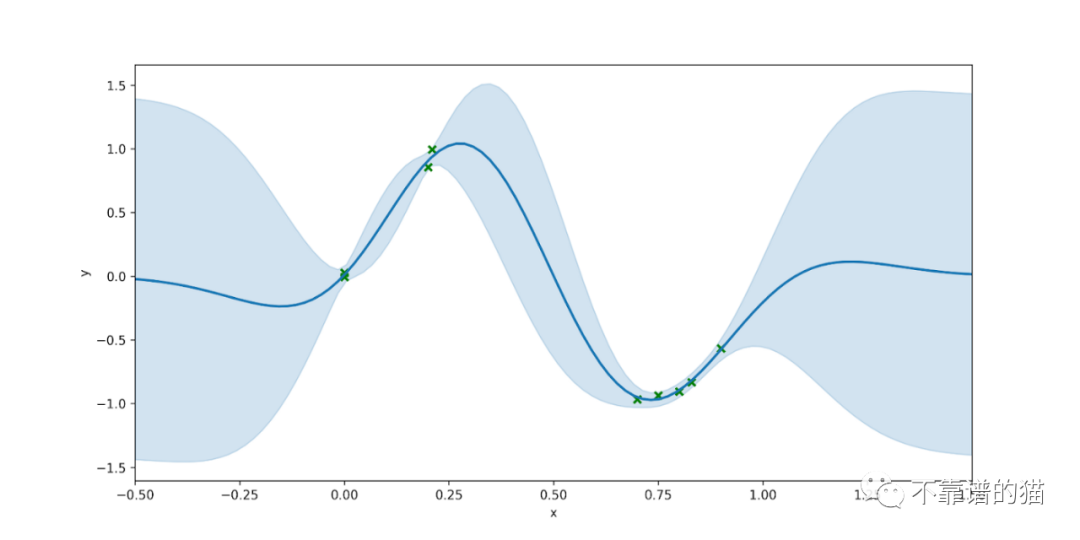
圖中的藍線代表預測的平均值，藍色陰影區域代表預測方差或總不確定性。正如預期的那樣，該模型對其在觀測數據附近的預測更有信心，并且隨著我們遠離這些數據，不確定性將會增加。

如果您對實現感興趣，這里是使用 Python 和 GPflow生成最后一個圖形的代碼：

import matplotlib.pyplot as plt
import numpy as np
import gpflow
# 生成數據的函數
def f(x):
    return np.sin(2*np.pi*x)
# 我們生成一些假設高斯加性噪聲的數據
X = np.array([0, 0, 0.2, 0.21, 0.7, 0.75, 0.8, 0.83, 0.9])
N = len(X)
epsilon = np.random.normal(scale=0.1, size=N)
y = f(X) + epsilon
X = X.reshape(-1, 1)
y = y.reshape(-1, 1)
# Plot the problem
plt.figure(figsize=(12, 6))
plt.plot(X, y, "kx", mew=2, c="g")
plt.xlabel("x")
plt.ylabel("y")
plt.savefig("problem.png", dpi=300)
# 定義核
kernel = gpflow.kernels.RBF()
# 構建模型
model = gpflow.models.GPR(data=(X, y), kernel=kernel, mean_function=None)
# Train the model
opt = gpflow.optimizers.Scipy()
opt.minimize(model.training_loss, model.trainable_variables) 
# 生成用于預測的測試點
x_test = np.linspace(-0.5, 1.5, 100).reshape(100, 1)  # test points must be of shape (N, D)
## predict mean and variance of latent GP at test points
mean, var = model.predict_f(x_test)
## 繪制預測
plt.figure(figsize=(12, 6))
plt.plot(X, y, "kx", mew=2, c="g")
plt.plot(x_test, mean, "C0", lw=2)
plt.fill_between(
    xx[:, 0],
    mean[:, 0] - 2 * np.sqrt(var[:, 0]),
    mean[:, 0] + 2 * np.sqrt(var[:, 0]),
    color="C0",
    alpha=0.2,
)
_ = plt.xlim(-0.5, 1.5)
plt.xlabel("x")
plt.ylabel("y")
plt.show()

結論

在本文中，我們看到一些機器學習模型可能在訓練數據之外給出過度自信的預測，這在實際應用中可能成為一個問題。我們還展示了高斯過程模型如何給不確定性進行估計。