一種基于神經網絡的策略,可增強量子模擬
近期的量子計算機為尋找量子系統的基態提供了一個有前途的平臺,這是物理學、化學和材料科學中的一項基本任務。然而,近期方法受到噪聲影響以及近期量子硬件資源有限的限制。
加拿大滑鐵盧大學的研究人員引入了神經誤差緩解,它使用神經網絡來改進使用近期量子模擬獲得的基態和基態可觀測值的估計。為了證明該方法的廣泛適用性,研究人員采用神經誤差緩解來找到通過變分量子本征求解器制備的 H2 和 LiH 分子哈密頓量以及晶格 Schwinger 模型的基態。
實驗結果表明,神經誤差緩解改進了數值和實驗變分量子特征求解器計算,以產生低能量誤差、高保真度和對更復雜的可觀察量(例如階參數和糾纏熵)的準確估計,而無需額外的量子資源。此外,神經誤差緩解與所使用的量子態準備算法、實現它的量子硬件以及影響實驗的特定噪聲通道無關,有助于其作為量子模擬工具的多功能性。
該研究以「Neural Error Mitigation of Near-Term Quantum Simulations」為題,于 2022 年 7 月 20 日發布在《Nature Machine Intelligence》。

自 20 世紀初以來,科學家們一直在開發描述量子力學系統行為的綜合理論。然而,研究這些系統所需的計算成本往往超過當前科學計算方法和硬件的能力。因此,計算不可行性仍然是這些理論在科學和技術問題上的實際應用的障礙。
量子計算機上的量子系統模擬(這里稱為量子模擬)顯示出克服這些障礙的希望,并且一直是量子計算機概念和創造背后的基礎驅動力。特別是,超出經典計算機能力的量子多體系統的基態和穩態的量子模擬預計將對核物理、粒子物理、量子引力、凝聚態物理、量子化學和材料科學產生重大影響。當前和近期量子計算機的能力繼續受到量子比特數量和噪聲影響等限制的限制。量子糾錯技術可以消除由噪聲引起的錯誤,為容錯量子計算提供了一條途徑。然而,在實踐中,實現量子糾錯會在所需的量子比特數和低錯誤率方面產生很大的開銷,這兩者都超出了當前和近期設備的能力。
在可以實現容錯量子模擬之前,現代變分算法大大減輕了對量子硬件的需求,并利用了嘈雜的中等規模量子設備的能力。
一個突出的例子是變分量子本征求解器 (VQE),這是一種混合量子經典算法,它通過一系列參數化量子電路的變分優化迭代地逼近目標哈密頓量的最低能量本征值。在其他變分算法中,這已成為使用近期設備實現量子優勢并加速多個科學和技術領域進展的領先策略。
變分量子算法的實驗實現對于許多科學問題來說仍然是一個挑戰,因為嘈雜的中等規模量子設備會受到各種噪聲源和缺陷的影響。當前,已經提出了幾種用于緩解這些問題的量子誤差緩解 (QEM) 方法并經過實驗驗證,從而在沒有量子糾錯所需的量子資源的情況下改進了量子計算。
通常,這些方法使用有關影響量子計算、硬件實現或量子算法本身的噪聲通道的特定信息;包括噪聲模型的隱含表征以及它們如何影響對所需可觀察量的估計、準備好的量子態應該駐留的狀態子空間的特定知識以及量子計算的各個組件上噪聲源的表征和緩解 ,例如單量子比特和雙量子比特門錯誤,以及狀態準備和測量誤差。
機器學習技術最近被重新用作解決量子多體物理和量子信息處理中復雜問題的工具,為 QEM 提供了另一種途徑。在這里,滑鐵盧大學的研究人員介紹了一種名為神經誤差緩解(NEM)的 QEM 策略,它使用神經網絡來緩解哈密頓量的量子基態的近似準備中的錯誤。
NEM 算法由兩個步驟組成。首先,研究人員進行了神經量子態 (NQS) 斷層掃描 (NQST) 以訓練 NQS ansatz 來表示由噪聲量子設備使用實驗可訪問的測量準備的近似基態。受傳統量子態斷層掃描 (QST) 的啟發,NQST 是一種數據驅動的 QST 機器學習方法,它使用有限數量的測量來有效地重建復雜的量子態。
然后,在相同的 NQS ansatz(也被稱為 NEM ansatz)上應用變分蒙特卡洛(VMC)算法來改進未知基態的表示。本著 VQE 的精神,VMC 在經典變分 ansatz 的基礎上逼近哈密頓量的基態,在示例中為 NQS ansatz。
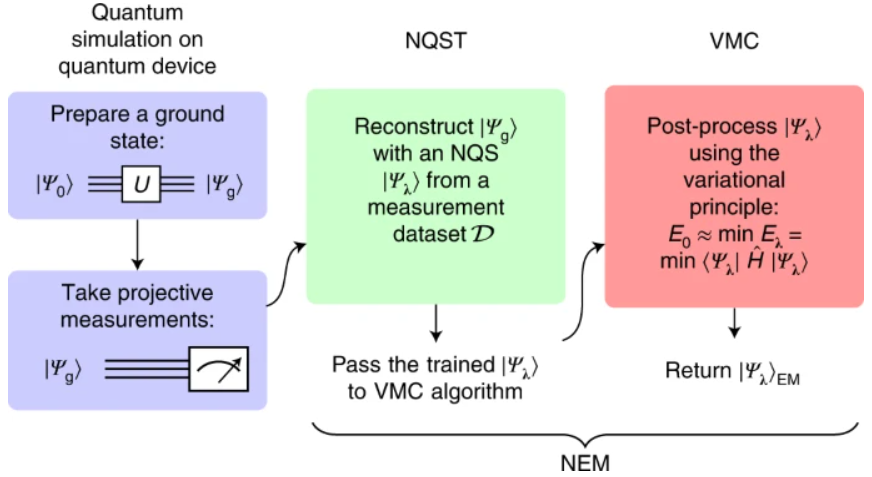
圖示:NEM 程序。(來源:論文)
在這里,研究人員使用自回歸生成神經網絡作為 NEM ansatz;更具體地說,他們使用了 Transformer 架構,并表明該模型作為 NQS 表現良好。由于它能夠模擬長程時間和空間相關性,這種架構已被用于自然語言和圖像處理領域的許多最先進的實驗中,并且具有模擬長程量子相關性的潛力。
與其他錯誤緩解技術相比,NEM 有幾個優點。首先,它的實驗開銷低;它只需要一組簡單的實驗上可行的測量來學習由 VQE 制備的噪聲量子態的特性。因此,NEM 中錯誤緩解的開銷從量子資源(即執行額外的量子實驗和測量)轉移到用于機器學習的經典計算資源。特別是,研究人員注意到 NEM 的主要成本是在收斂之前執行 VMC。NEM 的另一個優點是它與量子模擬算法、實現它的設備以及影響量子模擬的特定噪聲通道無關。因此,它也可以與其他 QEM 技術相結合,并可以應用于模擬量子模擬或數字量子電路。
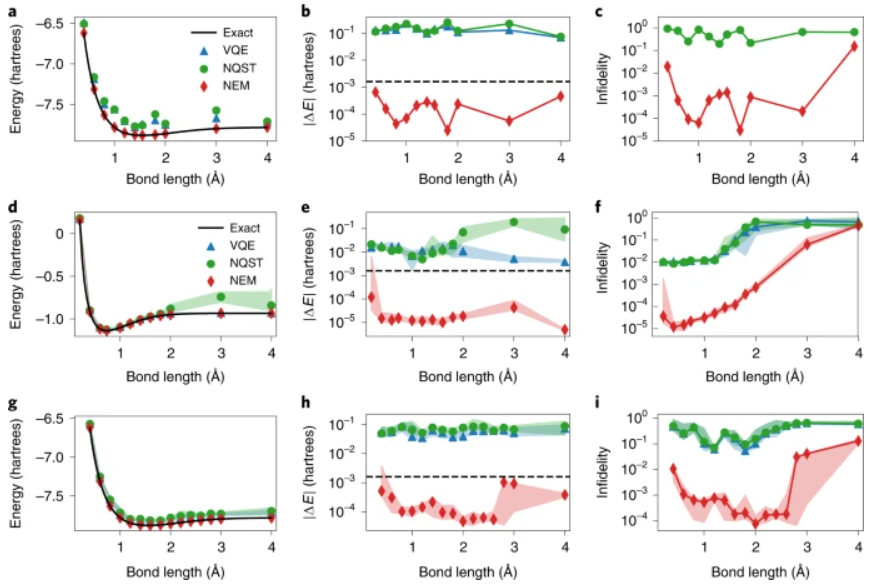
圖示:分子哈密頓量的實驗和數值 NEM 結果。(來源:論文)
NEM 還解決了使用近期量子設備估計量子可觀測物時出現的低測量精度問題。這在量子模擬中尤為重要,在量子模擬中,準確估計量子可觀測量對于實際應用至關重要。NEM 從本質上解決了算法每一步測量精度低的問題。在第一步中,NQST 以引入小的估計偏差為代價來改進可觀察估計的方差。通過使用 VMC 訓練 NEM ansatz 可以進一步減少這種偏差以及剩余方差,這會在達到基態后導致能量估計的零方差期望值。
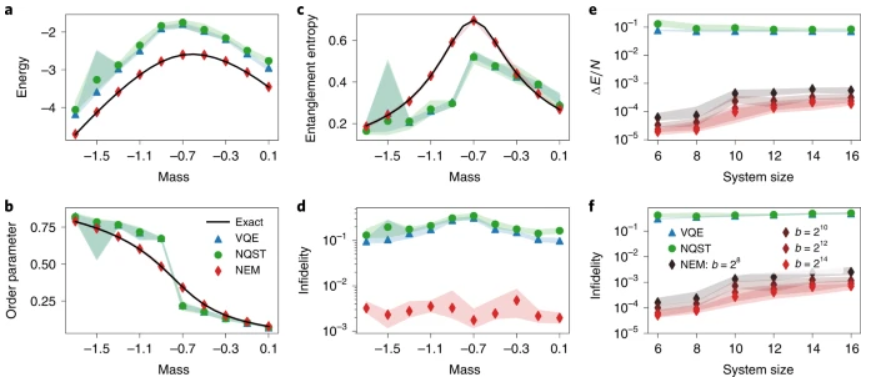
圖示:NEM 的性能應用于晶格 Schwinger 模型的基態。(來源:論文)
通過結合使用參數量子電路作為 ansatz 的 VQE,以及使用神經網絡作為 ansatz 的 NQST 和 VMC,NEM 將兩個參數量子狀態族和三個關于其損失情況的優化問題結合在一起。研究人員提出了這些狀態家族之間關系的性質、它們的損失情況和量子優勢的問題。檢查這些關系提供了一種新的方法來研究嘈雜的中等規模量子算法在尋求量子優勢方面的潛力。這可能會促進在經典易處理的量子系統模擬和需要量子資源的模擬之間獲得更好地劃分。
論文鏈接:?https://www.nature.com/articles/s42256-022-00509-0?
相關報道:?https://techxplore.com/news/2022-08-neural-networkbased-strategy-near-term-quantum.html?





































