機器學習基礎之數字上的距離:點在空間中的距離
本文轉載自微信公眾號「活在信息時代」,作者活在信息時代。轉載本文請聯系活在信息時代公眾號。
在機器學習中,一個基礎的概念就是如何判斷兩個樣本之間的差異,從而能夠評價兩個樣本之間的相似性和類別等信息。而判斷這種相似性的度量就是兩個樣本在特征空間內的距離。
根據數據特征的不同,度量方法有很多種。一般而言,對兩個數據樣本x,y,定義一個函數d(x,y),如果定義其為兩個樣本之間的距離,那么d(x,y)則需要滿足以下幾條基本性質:
- 非負性:d(x,y)>=0
- 同一性:d(x,y)=0 ? x=y
- 對稱性:d(x,y)= d(y,x)
- 三角不等式:d(x,y)<= d(x,z)+d(z,y)
通常來講,常見的距離度量包括:點在空間中的距離、字符串間的距離、集合的相似度、變量/概念分布間的距離四種。
今天我們首先來介紹一下最為常用的點在空間中的距離。
點在空間中的距離包括以下幾種:
1、歐幾里得距離(Ecllidean Distance)
毫無疑問,歐氏距離是人們最熟悉的距離,它即是兩點之間的直線距離。學過初中數學的同學都知道在笛卡爾坐標系中如何計算二維空間兩個點之間的距離
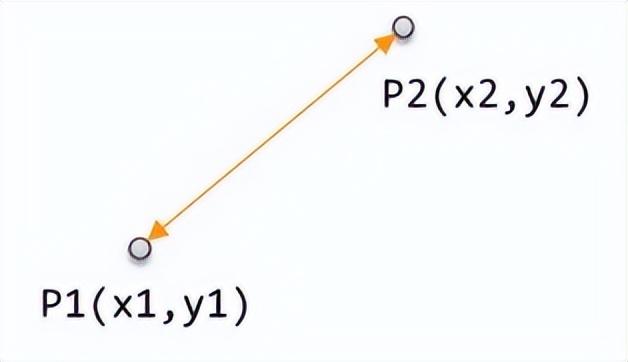
其計算公式為:
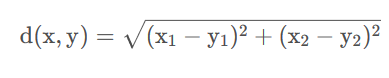
推廣到N維空間的歐氏距離即為:
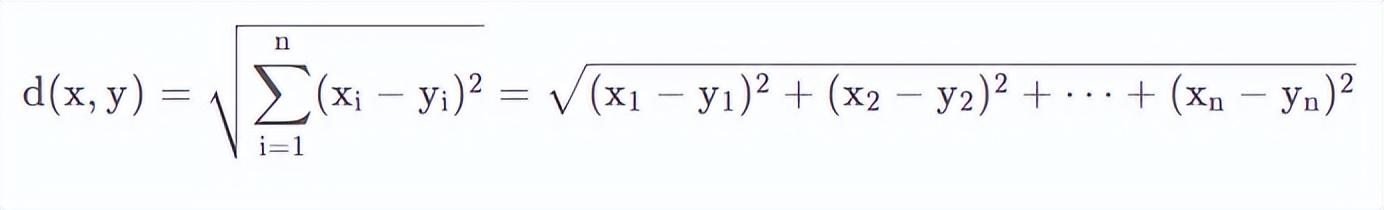
2、曼哈頓距離(Manhattan Distance)
曼哈頓距離又稱為出租車距離,其概念來源于紐約曼哈頓區這樣有很多橫平豎直的街區,在這種街區中,出租車司機如果想從一個點走到另一個點的話,計算直線距離是沒有用的,因為出租車不可能從建筑物上飛過去。因此,這種距離通常是將兩個點的東西向、南北向距離分別相減再相加,這也就是出租車實際要經過的距離。
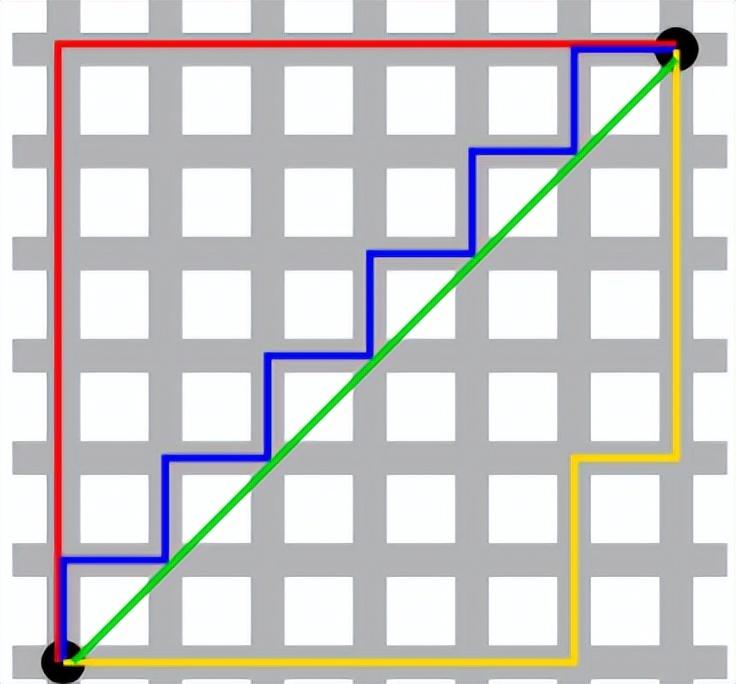
如圖所示,紅線和黃線就是兩種不同路徑的曼哈頓距離。數學上,二維空間的曼哈頓距離計算方法如下:
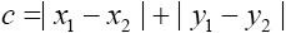
3、切比雪夫距離(Chebyshev Distance)
切比雪夫距離定義為兩個點之間各坐標數值差的最大值。
其最直觀的例子即是國際象棋中的國王,因為它可以橫走直走斜走,但是每次都只能走一格,所以切比雪夫距離就是他要走到另一個格子所需要的最小距離。
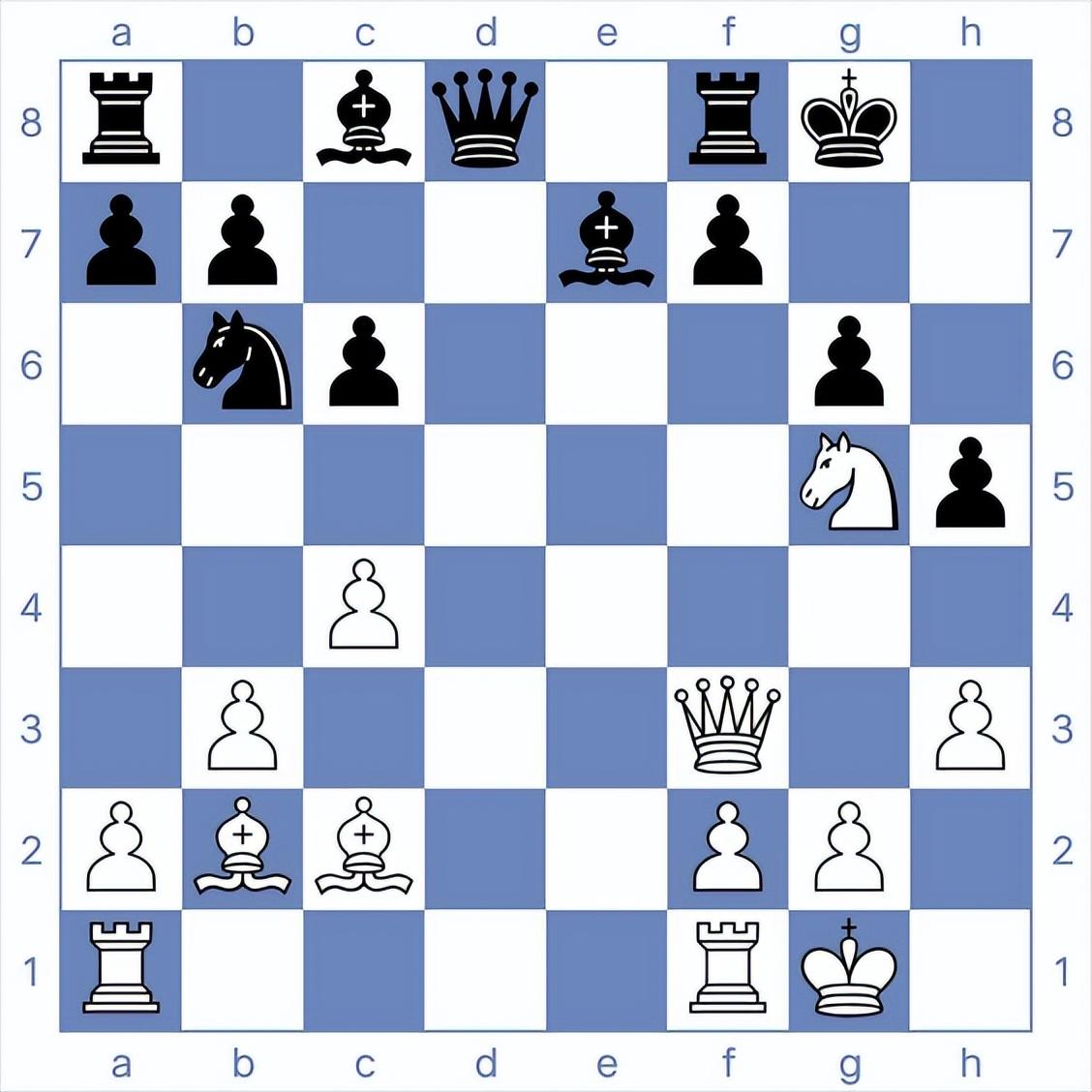
4、閔可夫斯基距離(Minkowski Distance)
閔氏距離本身不是一個特別的距離,而是將多個距離(曼哈頓距離、歐氏距離、切比雪夫距離)合并成為的一個公式。
其定義為,對于兩個n維變量,閔氏距離為:
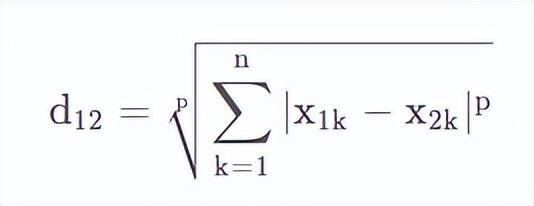
當p=1時,可以看到
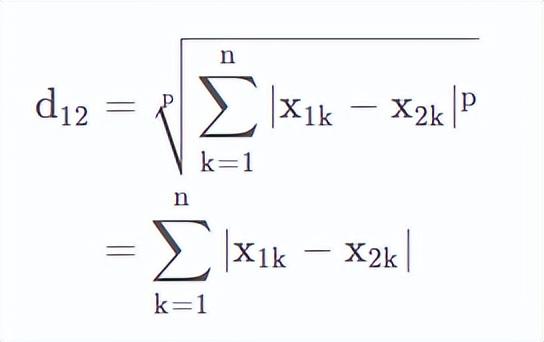
此時為曼哈頓距離。
當p=2時,可以看到
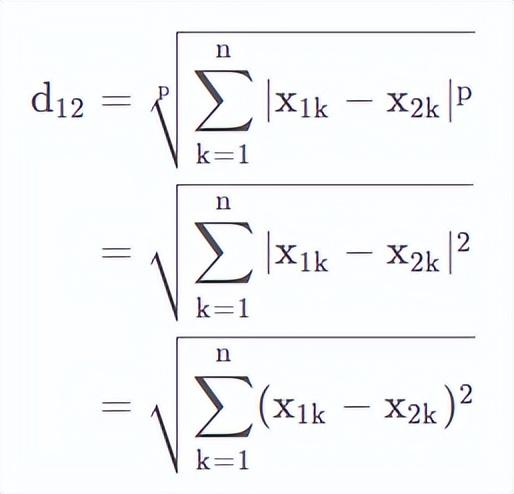
此時即為歐氏距離。
當p=∞時,可以看到
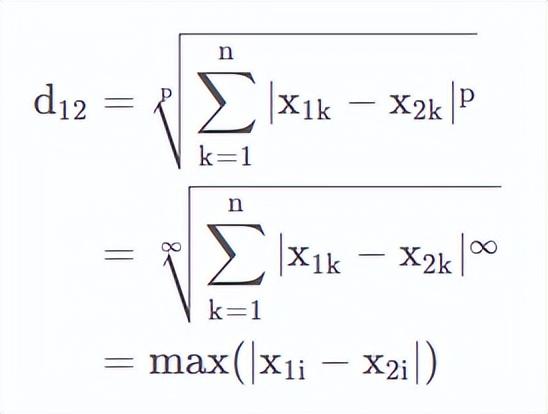
此時即為切比雪夫距離。
5、標準化的歐幾里得距離(Standardized Euclidean Distance)
歐氏距離可以測量兩個點之間的直線距離,但是在某些情況下,可能會受到單位不同的影響。例如同時是差5,差5毫米的身高和差5公斤的體重,觀感可能是完全不同的。如果我們想對三個模特進行聚類,她們各自的屬性如下:
A:65000000毫克(即65公斤),1.74米
B:60000000毫克(即60公斤),1.70米
C:65000000毫克(即65公斤),1.40米
按我們正常的理解,A和B是身材比較好的模特,應該歸到一類。但是以上述單位實際計算的時候,卻發現A和B的差異大于A和C之間的差異。原因在于屬性計量單位的不同導致數值差異過大。同樣的數據如果換個單位。
A:65千克,174厘米
B:60千克,170厘米
C:65千克,140厘米
那么就會得到我們想到的結果,將A和B歸為一類了。因此,為避免出現這種由于計量單位的不同而出現的差異,我們就需要引入標準化歐氏距離。在這種距離計算中,會將各個分量都標準化到均值、方差相等的區間。
假設樣本集X的均值(mean)為m,標準差(standard deviation)為s,那么X的“標準化變量”表示為:
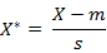
其中,標準化后的值 = ( 標準化前的值 - 分量的均值 ) /分量的標準差。經過簡單的推導就可以得到兩個n維向量間的標準化歐氏距離公式為:
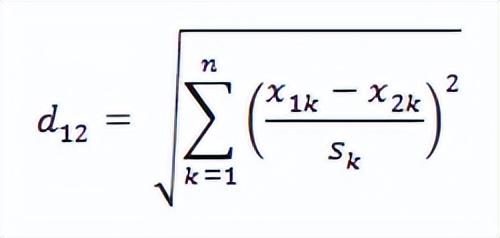
如果將方差的倒數看成是一個權重,這個公式可以看成是一種加權歐氏距離(Weighted Euclidean distance)。通過這種操作,我們就有效的消除了不同計重單位之間的差異。
6、蘭氏距離(Lance and Willianms Distance)
蘭氏距離又稱為堪培拉距離,
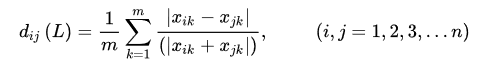
它是一個無量綱的指標,克服了閔氏距離與各指標的量綱有關的缺點,并且對于較大的奇異值不敏感,特別適合調度偏倚的數據。但是這種距離也沒有考慮到變量間的相關性。所以如果需要考慮變量之間的相關性的話,還是需要馬氏距離。
7、馬氏距離(Mahalanobis Distance)
對數值進行標準化之后,就一定不會出問題嗎?也不一定。例如在一個一維的例子中,如果有兩個類,一個類均值為0,方差為0.1,而另一個類均值為5,方差為5。那么如果一個值為2的點應該屬于哪一類呢?我們直覺上認為它肯定是第二類,因為第一類顯然不太可能在數值上達到2。但是實際上從距離上計算的話2這個數就得屬于第一類。
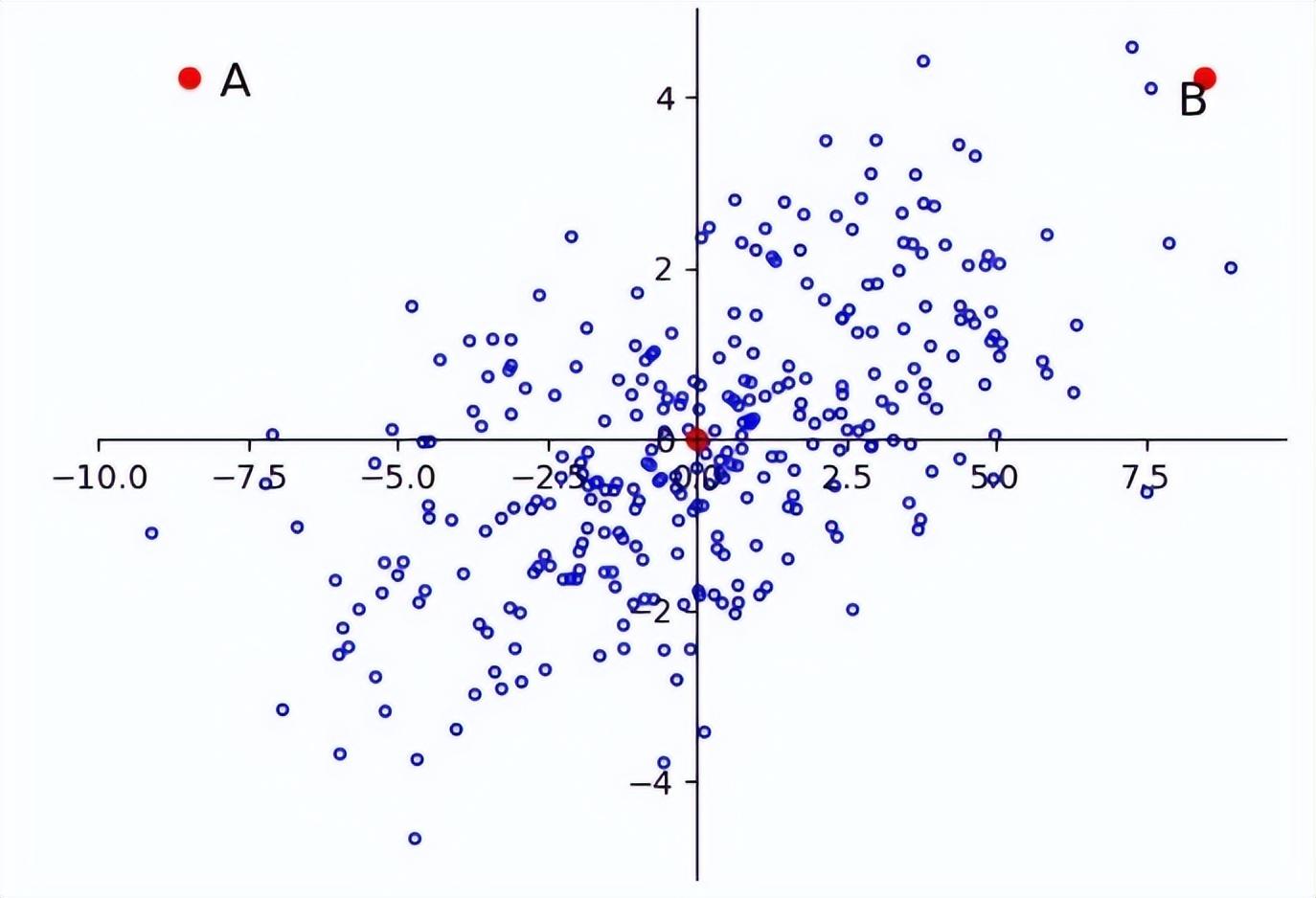
所以,在一個方差較小的維度下,很小的差別就可能成為離群點。例如說下圖,A與B相對于原點的距離是相同的,但是由于樣本整體沿著橫軸分布,所以B點更有可能是樣本中的點,而A點則更有可能是離群點。
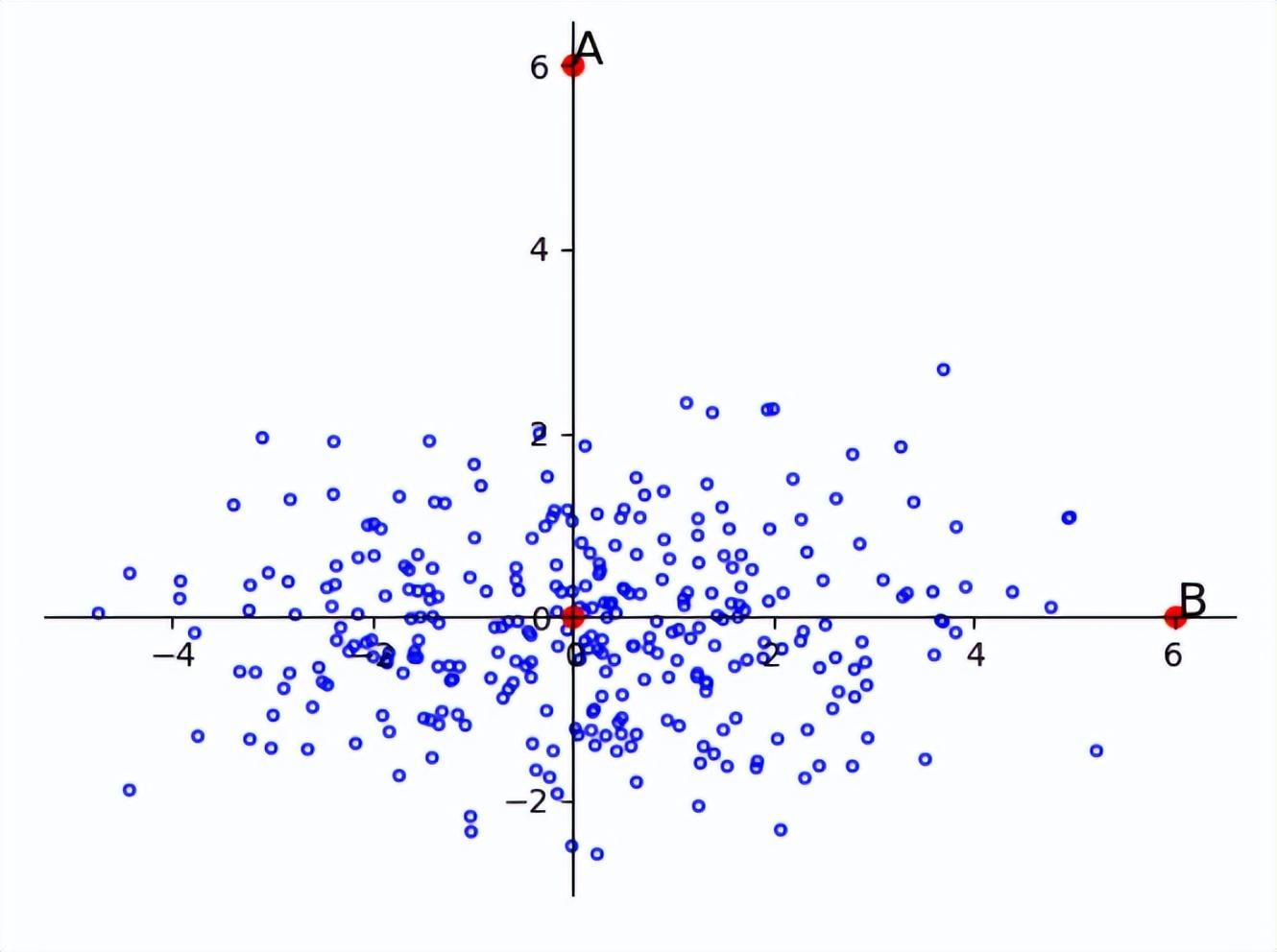
而在維度間不獨立同分布的情況下,也會出現問題,例如說下圖中的A點與B點到原點的距離相等,但是主要分布類似于f(x)=x,所以A更像是一個離群點。
因此,我們可以看到,在這種情況下,標準化的歐氏距離也會有問題,所以我們需要引入馬氏距離。
馬氏距離將變量按照主成分進行旋轉,讓維度間相互獨立,然后再進行標準化,讓維度同分布。而主成分即為特征向量方向,所以只需要按照特征向量的方向進行旋轉,然后縮放特征值倍就可以了。例如上圖變換之后會得到下面的結果:
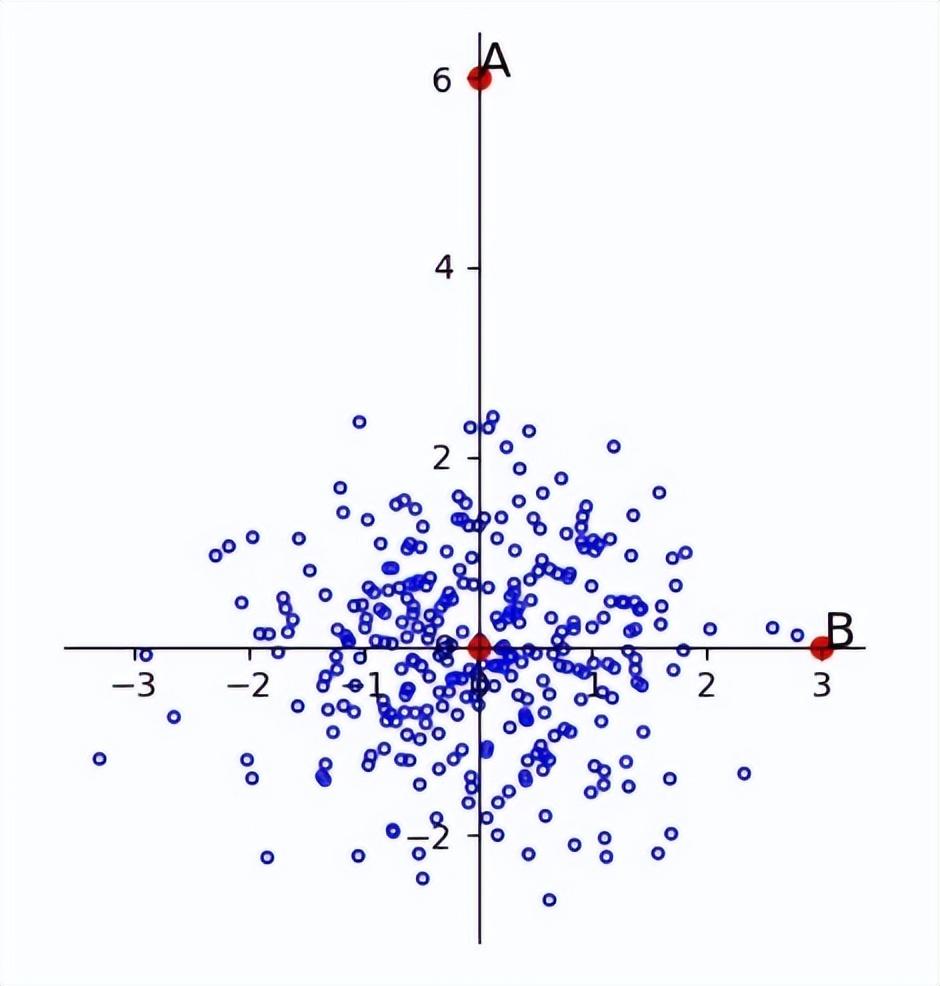
可以看出離群點被成功分離了。
馬氏距離是由印度數學家馬哈拉諾比斯提出的,表示數據的協方差距離。它是一種有效地計算兩個未知樣本集的相似度的方法。
對于一個均值為
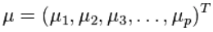
,協方差矩陣為Σ的多變量矢量
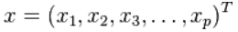
,其馬氏距離(單個數據點的馬氏距離)為:
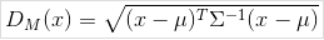
對于兩個服從同一分布并且其協方差矩陣為Σ的隨機變量X與Y的差異程度,數據點x, y之間的馬氏距離為:
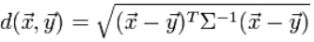
如果協方差矩陣為單位矩陣,那么馬氏距離就簡化成了歐氏距離。如果協方差矩陣為對角陣,那么馬氏距離就變成了標準化的歐氏距離。
8、余弦距離(Cosine Distance)
顧名思義,余弦距離來源于幾何中的夾角余弦,它可用來衡量兩個向量方向的差異,而非距離或長度上。當余弦值為0時,兩向量正交,夾角為90度。夾角越小,余弦值越接近于1,方向更趨同。
在N維空間中,余弦距離為:
值得指出的是,余弦距離不滿足三角不等式。
9、測地距離(Geodesic Distance)
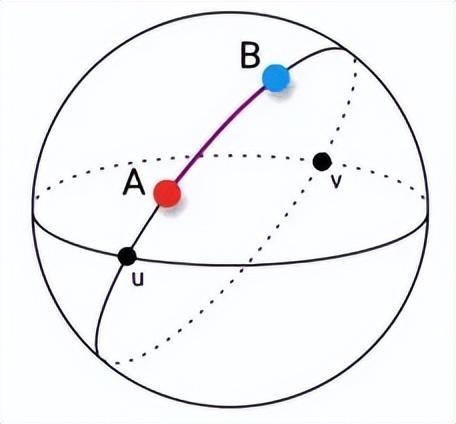
測地距離最初是指球體表面之間的最短距離。當特征空間為平面時,測地距離即為歐氏距離。在非歐幾何中,球面上兩點間距離最短的線是連接這兩點的大圓弧,在球面上的三角形、多邊形的邊也是由這些大圓弧組成的。
10、布雷柯蒂斯距離(Bray Curtis Distance)
布雷柯蒂斯距離主要用于植物學、生態學和環境科學,它可以用來計算樣本之間的差異。其公式為:
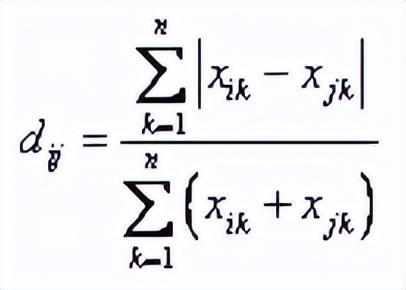
其取值在[0, 1]之間,如果兩個向量坐標都為0的話,那么值就無意義。