量子機器學習Variational Quantum Classifier (VQC)簡介
變分量子分類器(Variational Quantum Classifier,簡稱VQC)是一種利用量子計算技術進行分類任務的機器學習算法。它屬于量子機器學習算法家族,旨在利用量子計算機的計算能力,潛在地提升經典機器學習方法的性能。
VQC的基本思想是使用一個量子電路,也稱為變分量子電路,將輸入數據編碼并映射到量子態上。然后,使用量子門和測量操作對這些量子態進行操作,以提取與分類任務相關的特征。最后,處理測量結果,并將其用于為輸入數據分配類別標簽。
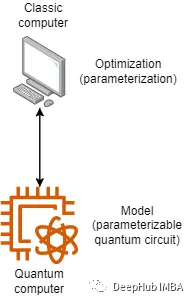
VQC將經典優化技術與量子計算相結合。在訓練過程中,將變分量子電路在量子計算機或模擬器上重復執行,并將結果與訓練數據的真實標簽進行比較。通過迭代地調整變分量子電路的參數,使其在預測標簽與真實標簽之間的差異上最小化代價函數。這個優化過程旨在找到最優的量子電路配置,從而最大化分類準確性。雖然看起來很簡單,但這種混合計算體系結構存在很多的挑戰。
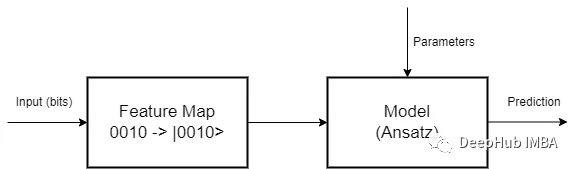
特征映射是第一階段,其中數據必須編碼為量子位。有許多編碼方法,因為特征映射是從一個向量空間到另一個向量空間的數學變換。所以研究如何為每個問題找到最佳映射,就是一個待研究的問題
有了映射,還要設計一個量子電路作為模型,這是第二階段。在這里我們可以隨心所愿地發揮創意,但必須考慮到同樣的舊規則仍然很重要:對于簡單的問題,不要使用太多的參數來避免過擬合,也不能使用太少的參數來避免偏差,并且由于我們正在使用量子計算,為了從量子計算范式中獲得最佳效果,必須與疊加(superposition )和糾纏(entanglement)一起工作。
并且量子電路是線性變換,我們還需要對其輸出進行處理。比如非線性化的激活。
數據集和特征
這里我們將基于泰坦尼克號數據集設計一個分類器,我們的數據集有以下特征:
- PassengerID
- Passenger name
- Class (First, second or third)
- Gender
- Age
- SibSP (siblings and/or spouses aboard)
- Parch (parents or children aboard)
- Ticket
- Fare
- Cabin
- Embarked
- Survived
我們要構建一個根據乘客的特征預測乘客是否幸存的分類器。所以我們只選擇幾個變量作為示例:
- is_child (if age <12)
- is_class1 (if person is in the first class)
- is_class2
- is_female
由于只有四個變量,所以我們使用將使用Basis Embedding。我們只需將經典位轉換為等效量子位。比如我們的四個變量是1010,這將被轉換為|1010>。
模型
我們的模型是可參數化量子電路。這個電路必須具有一定程度的疊加和糾纏,這樣才能證明使用量子組件是合理的,我們的模型如下:
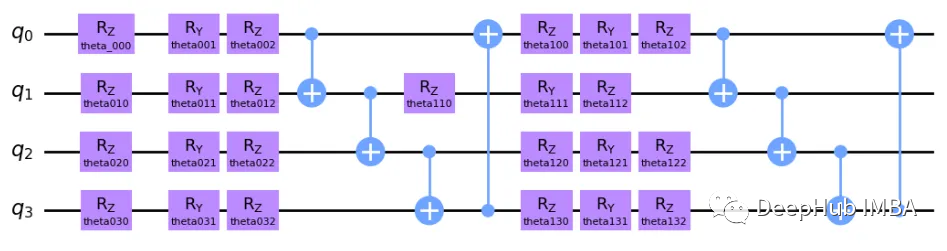
這個模型可能看起來很復雜,但他的想法相當簡單。 這是一個雙層電路,因為核心結構重復了 2 次。 首先,我們為每個量子位繞 Z、Y 和 Z 軸旋轉,這里的想法是分別在每個量子位上插入某種程度的疊加。 這些旋轉是參數化的,并且在算法的每次交互中,這些參數將由經典計算機更新。 然后就是 Y 軸和 Z 軸上的旋轉,因為量子位的矢量空間是一個球體(布洛赫球體)。 RZ 只會改變量子比特相位,RY 會影響量子比特與 |0> 和 |1> 的接近程度。
每對量子位之間有四個受控非 (CNOT) 狀態,這是一個量子門,根據另一個量子位(分別為目標和控制)的狀態反轉一個量子位狀態。 也就是說這個門糾纏了我們電路中的所有量子位,現在所有狀態都糾纏了。 在第二層中,我們應用了一組新的旋轉,這不僅僅是第一層的邏輯重復,因為現在所有狀態都糾纏在一起,這意味著旋轉第一個量子比特也會影響其他量子比特! 最后我們有了一組新的 CNOT 門。
這是對我們上面模型的非常簡單的解釋,下面代碼會讓這些內容變得更清晰。
優化器
我使用的是Adam Optimizer,但是這個優化器是經過特殊處理的,我們直接使用pennylane 庫。
代碼實現
這里我們直接使用Pennylane和sklearn實現代碼。
import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
import math
num_qubits = 4
num_layers = 2
dev = qml.device("default.qubit", wires=num_qubits)
# quantum circuit functions
def statepreparation(x):
qml.BasisEmbedding(x, wires=range(0, num_qubits))
def layer(W):
qml.Rot(W[0, 0], W[0, 1], W[0, 2], wires=0)
qml.Rot(W[1, 0], W[1, 1], W[1, 2], wires=1)
qml.Rot(W[2, 0], W[2, 1], W[2, 2], wires=2)
qml.Rot(W[3, 0], W[3, 1], W[3, 2], wires=3)
qml.CNOT(wires=[0, 1])
qml.CNOT(wires=[1, 2])
qml.CNOT(wires=[2, 3])
qml.CNOT(wires=[3, 0])
@qml.qnode(dev, interface="autograd")
def circuit(weights, x):
statepreparation(x)
for W in weights:
layer(W)
return qml.expval(qml.PauliZ(0))
def variational_classifier(weights, bias, x):
return circuit(weights, x) + bias
def square_loss(labels, predictions):
loss = 0
for l, p in zip(labels, predictions):
loss = loss + (l - p) ** 2
loss = loss / len(labels)
return loss
def accuracy(labels, predictions):
loss = 0
for l, p in zip(labels, predictions):
if abs(l - p) < 1e-5:
loss = loss + 1
loss = loss / len(labels)
return loss
def cost(weights, bias, X, Y):
predictions = [variational_classifier(weights, bias, x) for x in X]
return square_loss(Y, predictions)
# preparaing data
df_train = pd.read_csv('train.csv')
df_train['Pclass'] = df_train['Pclass'].astype(str)
df_train = pd.concat([df_train, pd.get_dummies(df_train[['Pclass', 'Sex', 'Embarked']])], axis=1)
# I will fill missings with the median
df_train['Age'] = df_train['Age'].fillna(df_train['Age'].median())
df_train['is_child'] = df_train['Age'].map(lambda x: 1 if x < 12 else 0)
cols_model = ['is_child', 'Pclass_1', 'Pclass_2', 'Sex_female']
X_train, X_test, y_train, y_test = train_test_split(df_train[cols_model], df_train['Survived'], test_size=0.10, random_state=42, stratify=df_train['Survived'])
X_train = np.array(X_train.values, requires_grad=False)
Y_train = np.array(y_train.values * 2 - np.ones(len(y_train)), requires_grad=False)
# setting init params
np.random.seed(0)
weights_init = 0.01 * np.random.randn(num_layers, num_qubits, 3, requires_grad=True)
bias_init = np.array(0.0, requires_grad=True)
opt = AdamOptimizer(0.125)
num_it = 70
batch_size = math.floor(len(X_train)/num_it)
weights = weights_init
bias = bias_init
for it in range(num_it):
# Update the weights by one optimizer step
batch_index = np.random.randint(0, len(X_train), (batch_size,))
X_batch = X_train[batch_index]
Y_batch = Y_train[batch_index]
weights, bias, _, _ = opt.step(cost, weights, bias, X_batch, Y_batch)
# Compute accuracy
predictions = [np.sign(variational_classifier(weights, bias, x)) for x in X_train]
acc = accuracy(Y_train, predictions)
print(
"Iter: {:5d} | Cost: {:0.7f} | Accuracy: {:0.7f} ".format(
it + 1, cost(weights, bias, X_train, Y_train), acc
)
)
X_test = np.array(X_test.values, requires_grad=False)
Y_test = np.array(y_test.values * 2 - np.ones(len(y_test)), requires_grad=False)
predictions = [np.sign(variational_classifier(weights, bias, x)) for x in X_test]
accuracy_score(Y_test, predictions)
precision_score(Y_test, predictions)
recall_score(Y_test, predictions)
f1_score(Y_test, predictions, average='macro')最后得到的結果如下:
Accuracy: 78.89%
Precision: 76.67%
Recall: 65.71%
F1: 77.12%為了比較,我們使用經典的邏輯回歸作為對比,
Accuracy: 75.56%
Precision: 69.70%
Recall: 65.71%
F1: 74.00%可以看到VQC比邏輯回歸模型稍微好一點!這并不意味著VQC一定更好,因為只是這個特定的模型和特定的優化過程表現得更好。但這篇文章的主要還是是展示構建一個量子分類器是很簡單的,并且是有效的。
總結
VQC算法需要同時利用經典資源和量子資源。經典部分處理優化和參數更新,而量子部分在量子態上執行計算。VQC的性能和潛在優勢取決于諸如分類問題的復雜性、量子硬件的質量以及合適的量子特征映射和量子門的可用性等因素。
最重要的是:量子機器學習領域仍處于早期階段,VQC的實際實現和有效性目前受到構建大規模、糾錯的量子計算機的挑戰所限制。但是該領域的研究正在不斷進行,量子硬件和算法的進步可能會在未來帶來更強大和高效的量子分類器。





































