時間序列的季節(jié)性:3種模式及8種建模方法
分析和處理季節(jié)性是時間序列分析中的一個關(guān)鍵工作,在本文中我們將描述三種類型的季節(jié)性以及常見的8種建模方法。
什么是季節(jié)性?
季節(jié)性是構(gòu)成時間序列的關(guān)鍵因素之一,是指在一段時間內(nèi)以相似強度重復的系統(tǒng)運動。
季節(jié)變化可以由各種因素引起,例如天氣、日歷或經(jīng)濟條件。各種應用程序中都有這樣的例子。由于假期和旅游的緣故,夏天的機票更貴。另一個例子是消費者支出,由于因為12月的假期而增加。
季節(jié)性是指某些時期的平均值與其他時期的平均值不同。這個問題導致該系列是非平穩(wěn)的。這就是為什么在建立模型時分析季節(jié)性是很重要的。
3種模式
在時間序列中可以出現(xiàn)三種類型的季節(jié)模式。季節(jié)性可以是確定性的,也可以是隨機的。在隨機方面,季節(jié)模式可能是平穩(wěn)的,也可能不是。
這些季節(jié)性并不是相互排斥的。時間序列可以同時具有確定性和隨機季節(jié)性成分。
1、確定的季節(jié)性
具有確定性季節(jié)性的時間序列具有恒定的季節(jié)模式。它總是以一種可預測的方式出現(xiàn),無論是在強度上還是在周期性上:
相似強度:在同一季節(jié)期間,季節(jié)+模式的水平保持不變;
不變周期性:波峰和波谷的位置不改變。也就是說季節(jié)模式每次重復之間的時間是恒定的。
比如說下面這個就是一個具有確定性季節(jié)性的合成月時間序列:
import numpy as np
period = 12
size = 120
beta1 = 0.3
beta2 = 0.6
sin1 = np.asarray([np.sin(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
cos1 = np.asarray([np.cos(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
xt = np.cumsum(np.random.normal(scale=0.1, size=size))
series_det = xt + beta1*sin1 + beta2*cos1 + np.random.normal(scale=0.1, size=size)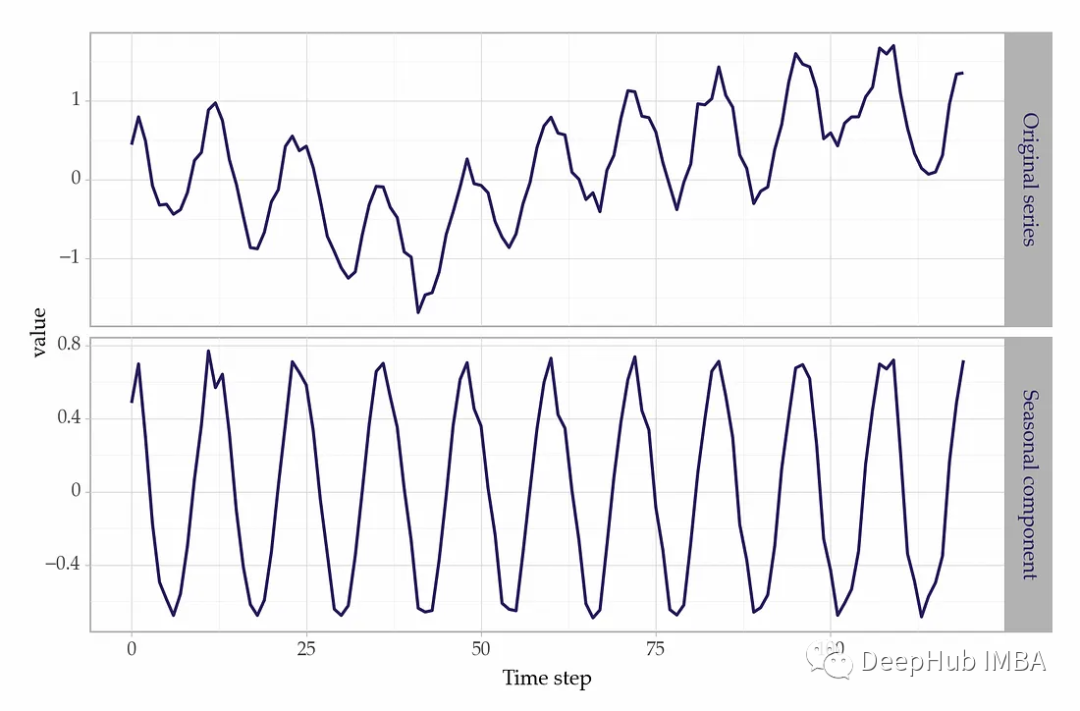
我們也可以用傅里葉級數(shù)來模擬季節(jié)性。傅里葉級數(shù)是不同周期的正弦和余弦波。如果季節(jié)性是確定性的,那么用傅里葉級數(shù)來描述是非常準確的。
2、隨機平穩(wěn)的季節(jié)性
beta1 = np.linspace(-.6, .3, num=size)
beta2 = np.linspace(.6, -.3, num=size)
sin1 = np.asarray([np.sin(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
cos1 = np.asarray([np.cos(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
xt = np.cumsum(np.random.normal(scale=0.1, size=size))
# synthetic series with stochastic seasonality
series_stoc = xt + beta1*sin1 + beta2*cos1 + np.random.normal(scale=0.1, size=size)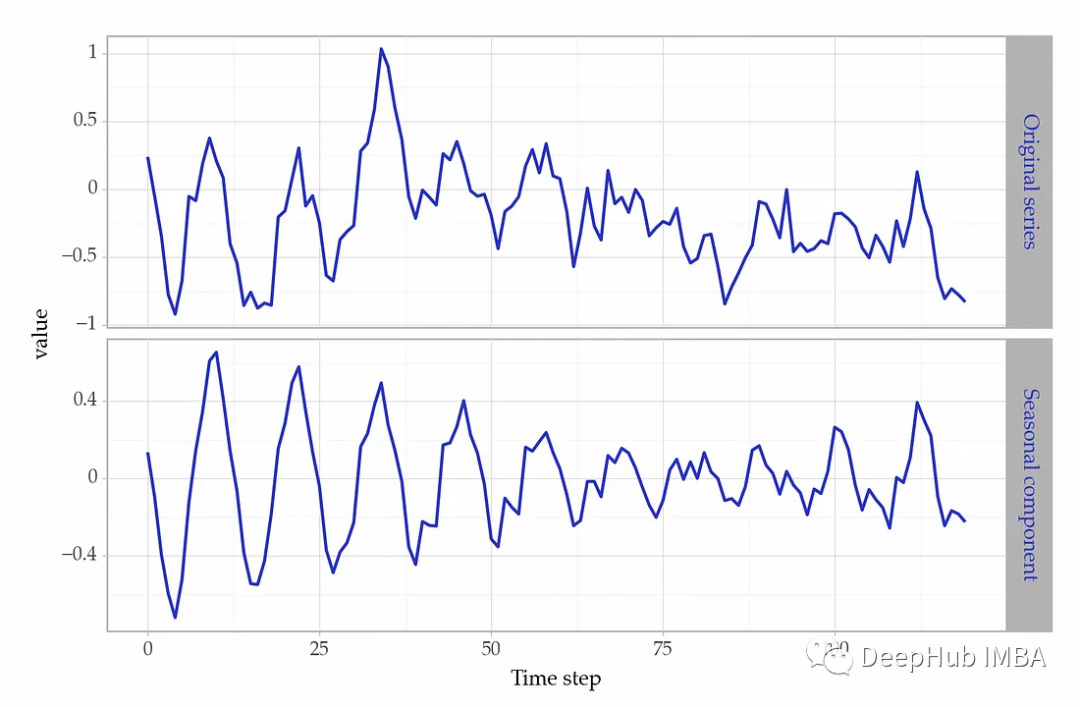
在連續(xù)的季節(jié)周期(如一年)中隨機平穩(wěn)的季節(jié)性演變。雖然強度難以預測,但周期性大致保持不變。
有了確定性的季節(jié)性,給定月份的預測不會隨年份而改變。對于隨機平穩(wěn)季節(jié)性,最佳猜測取決于前一年同月的值。
3、隨機非平穩(wěn)季節(jié)性
季節(jié)模式會在幾個季節(jié)期間發(fā)生顯著變化,這種季節(jié)性的周期性也隨著時間的推移而變化。這意味著波峰和波谷的位置不同。
這種季節(jié)性模式的例子出現(xiàn)在不同的領(lǐng)域。這些數(shù)據(jù)包括消費系列或工業(yè)生產(chǎn)數(shù)據(jù)。當時間序列具有綜合季節(jié)性時,變化很難預測。
季節(jié)性時間序列的測試
可視化時間序列是一種檢查季節(jié)模式的簡單方法。但是可視化并不能系統(tǒng)的說明季節(jié)性的模式,所以就需要更系統(tǒng)的方法來描述時間序列的而季節(jié)性。
1、測量季節(jié)強度
我們可以根據(jù)以下方法量化季節(jié)模式的強度:
import pandas as pd
from statsmodels.tsa.api import STL
def seasonal_strength(series: pd.Series) -> float:
# time series decomposition
series_decomp = STL(series, period=period).fit()
# variance of residuals + seasonality
resid_seas_var = (series_decomp.resid + series_decomp.seasonal).var()
# variance of residuals
resid_var = series_decomp.resid.var()
# seasonal strength
result = 1 - (resid_var / resid_seas_var)
return result這個函數(shù)估計季節(jié)性的強度,不管它是確定性的還是隨機的。
# strong seasonality in the deterministic series
seasonal_strength(series_det)
# 0.93
# strong seasonality in the stochastic series
seasonal_strength(series_stoc)
# 0.91如果該值高于0.64[2],則需要應用季節(jié)性差異過濾器。另一種檢測季節(jié)性的方法是QS測試,它在季節(jié)性滯后時檢查自相關(guān)性。
2、檢測非平穩(wěn)季節(jié)性
有一些統(tǒng)計檢驗是用來檢驗季節(jié)模式是否是非平穩(wěn)的。
一個常見的例子是Canova-Hansen (CH)測試。其假設如下:
- H0(零假設):季節(jié)模式平穩(wěn)(無季節(jié)單位根);
- H1:該系列包含一個季節(jié)性單位根
OCSB測試和HEGY測試是CH的兩種替代方法。這些方法都可以在Python的pmdarima 庫中找到。
from pmdarima.arima import nsdiffs
period = 12 # monthly data
nsdiffs(x=series_det, m=period, test='ch')
nsdiffs(x=series_det, m=period, test='ocsb')
nsdiffs(x=series_stoc, m=period, test='ch')
nsdiffs(x=series_stoc, m=period, test='ocsb')函數(shù)nsdiffs返回使序列平穩(wěn)所需的季節(jié)差步數(shù)。
3、相關(guān)性檢測
還有其他專為季節(jié)數(shù)據(jù)設計的檢測。例如,季節(jié)性肯德爾檢驗是一種非參數(shù)檢驗,用于檢查季節(jié)性時間序列的單調(diào)趨勢。
檢測季節(jié)性模式
季節(jié)性指的是在一段時間內(nèi)重復出現(xiàn)的模式。這是一個重要的變化來源,對建模很重要。
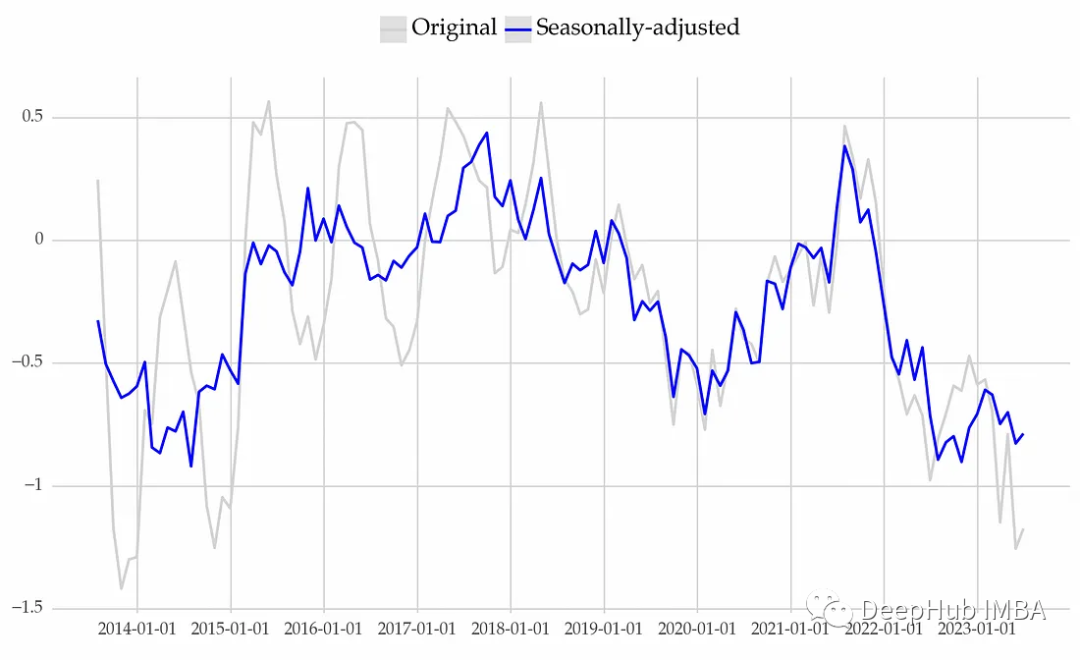
有很多種種處理季節(jié)性的方法,其中一些方法在建模之前去掉了季節(jié)成分。經(jīng)季節(jié)調(diào)整的數(shù)據(jù)(時間序列減去季節(jié)成分)強調(diào)長期影響,如趨勢或商業(yè)周期。而另外一些方法增加了額外的變量來捕捉季節(jié)性的周期性。
在討論不同的方法之前,先創(chuàng)建一個時間序列并描述它的季節(jié)模式,我們還繼續(xù)使用上面的代碼
period = 12 # monthly series
size = 120
beta1 = np.linspace(-.6, .3, num=size)
beta2 = np.linspace(.6, -.3, num=size)
sin1 = np.asarray([np.sin(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
cos1 = np.asarray([np.cos(2 * np.pi * i / 12) for i in np.arange(1, size + 1)])
xt = np.cumsum(np.random.normal(scale=0.1, size=size))
yt = xt + beta1 * sin1 + beta2 * cos1 + np.random.normal(scale=0.1, size=size)
yt = pd.Series(yt)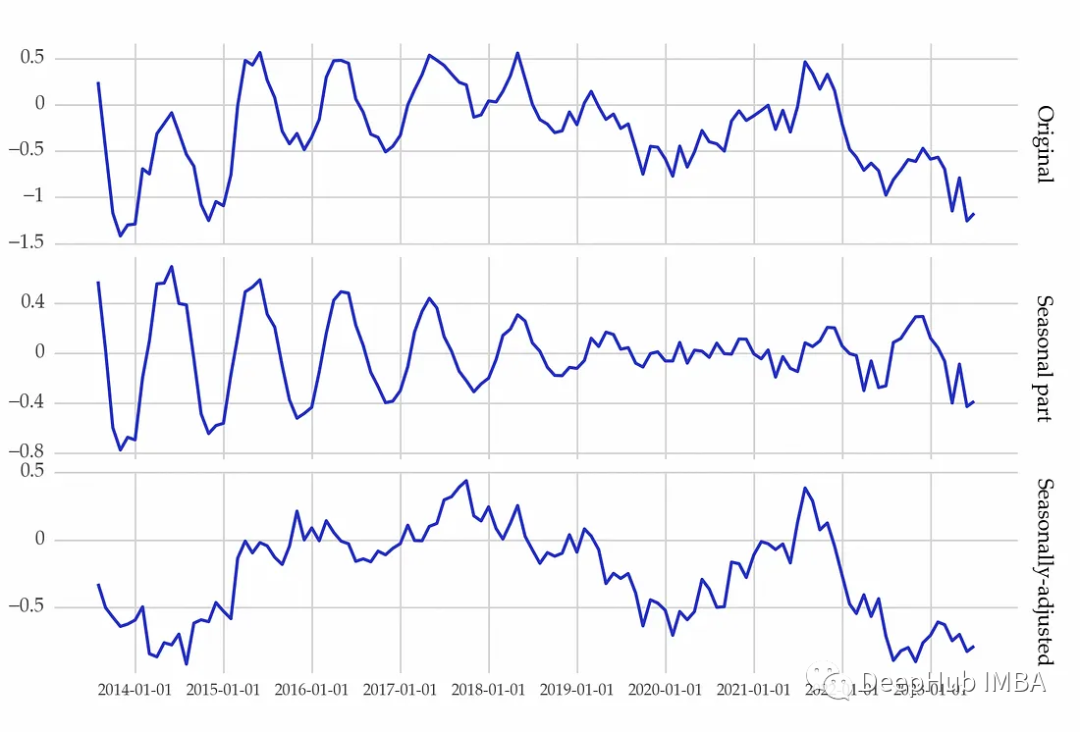
然后通過強度來描述季節(jié)模式:
seasonal_strength(yt, period=12)
# 0.90結(jié)果為0.90,表明季節(jié)性確實很強。該時間序列的自相關(guān)圖如下圖所示:
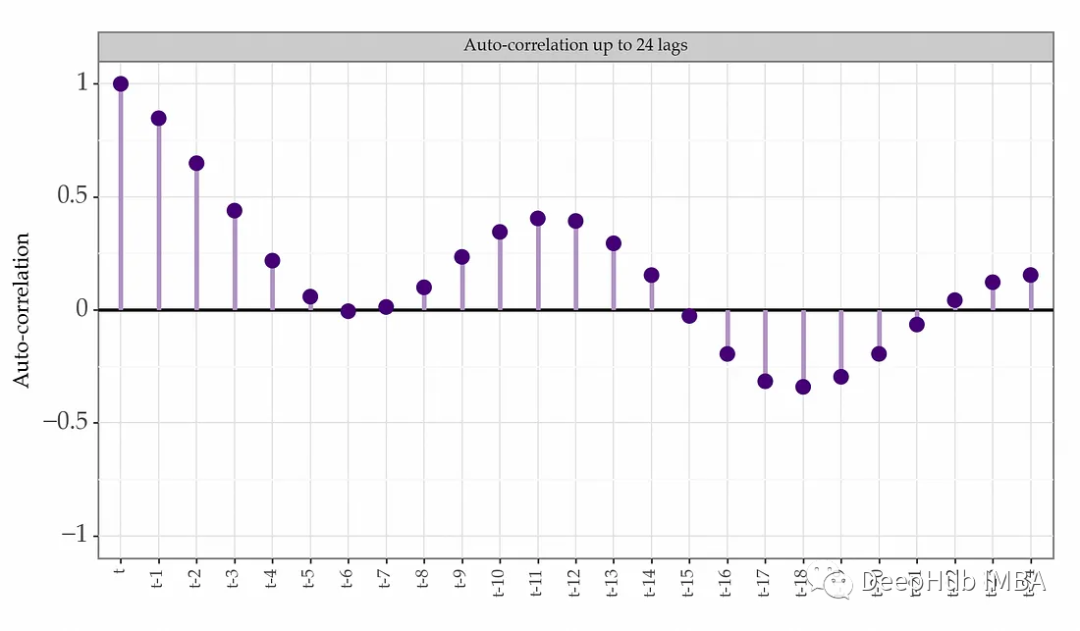
再使用我們上面介紹的Canova-Hansen檢驗來查看季節(jié)性單位根:
from pmdarima.arima import nsdiffs
nsdiffs(x=yt, m=period, test='ch')
# 0結(jié)果為0,表示不存在季節(jié)單位根。也就是說季節(jié)模式是平穩(wěn)的。
那么,我們該如何應對像這樣的季節(jié)性模式呢?
季節(jié)性建模
1、虛擬變量
季節(jié)性虛擬變量是一組二元變量。它們表示一個觀測值是否屬于一個給定的時期(例如一月)。
下面是一個如何創(chuàng)建這些變量的例子:
from sktime.transformations.series.date import DateTimeFeatures
from sklearn.preprocessing import OneHotEncoder
monthly_feats = DateTimeFeatures(ts_freq='M',
keep_original_columns=False,
feature_scope='efficient')
datetime_feats = monthly_feats.fit_transform(yt)
datetime_feats = datetime_feats.drop('year', axis=1)
encoder = OneHotEncoder(drop='first', sparse=False)
encoded_feats = encoder.fit_transform(datetime_feats)
encoded_feats_df = pd.DataFrame(encoded_feats,
columns=encoder.get_feature_names_out(),
dtype=int)這段代碼產(chǎn)生如下數(shù)據(jù)。
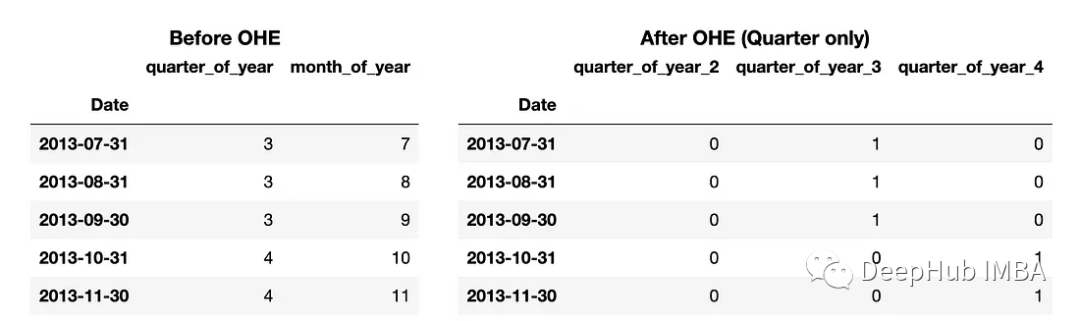
在每個觀察中獲得有關(guān)季度和月份的信息(左側(cè)表)。該信息存儲在datetime_feats對象中。然后使用one-hot編碼來創(chuàng)建虛擬變量(右側(cè)表)。
如果季節(jié)性是確定的,那么季節(jié)虛擬變量是非常有效。因為確定的季節(jié)性種季節(jié)模式是固定的,也就是強度和周期性基本不變。并且我們還可以通過檢驗季節(jié)虛擬變量的系數(shù)來分析季節(jié)效應及其變化,這有利于模型的可解釋性。
但是季節(jié)性虛擬變量的缺點也很明顯,它假設不同的時期是獨立的。比如1月份的觀測結(jié)果與12月份的觀測結(jié)果相關(guān)。虛擬變量對這種相關(guān)性視而不見。所以如果季節(jié)模式發(fā)生變化,虛擬變量就會產(chǎn)生很多問題。
2、傅里葉級數(shù)
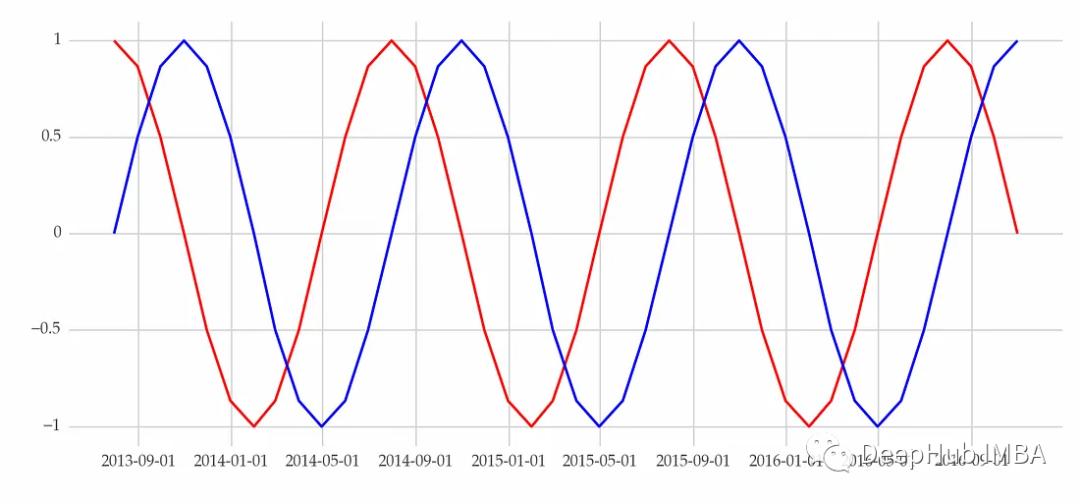
傅里葉級數(shù)是基于正弦和余弦波的周期性和確定性的變量。與季節(jié)性虛擬變量相反,這些三角函數(shù)將季節(jié)性建模為周期性模式,并且這種結(jié)構(gòu)更能反映現(xiàn)實。
sktime中包含了很好的方法:
from sktime.transformations.series.fourier import FourierFeatures
fourier = FourierFeatures(sp_list=[12],
fourier_terms_list=[4],
keep_original_columns=False)
fourier_feats = fourier.fit_transform(yt)這里需要指定兩個主要參數(shù):
- sp_list:將季節(jié)期間作為一個列表(例如,12個月的數(shù)據(jù))
- fourier_terms_list:項的個數(shù),指要包含的正弦和余弦級數(shù)的個數(shù)。這些都會影響到表示的平滑度。
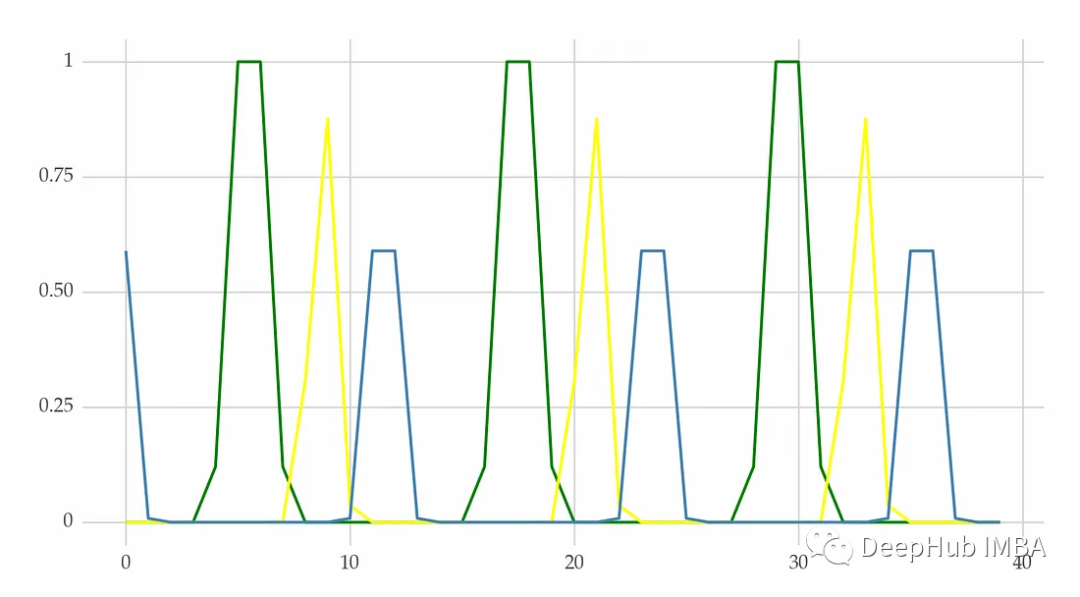
傅里葉級數(shù)是可以添加到模型中的解釋變量。并且可以將這些特性與滯后特性結(jié)合起來。
3、徑向基函數(shù)
徑向基函數(shù)(RBF)是傅里葉級數(shù)的替代方法。它他用過創(chuàng)建重復的鐘形曲線來模擬重復的圖案。
在scikit-lego包中有一個RepeatingBasisFunction方法:
from sklego.preprocessing import RepeatingBasisFunction
rbf_encoder = RepeatingBasisFunction(n_periods=4,
column='month_of_year',
input_range=(1, 12),
remainder='drop',
width=0.25)
rbf_features = rbf_encoder.fit_transform(datetime_feats)
rbf_features_df = pd.DataFrame(rbf_features,
columns=[f'RBF{i}'
for i in range(rbf_features.shape[1])])該方法最重要的三個參數(shù)如下:
- n_periods:要包含的基函數(shù)的個數(shù)
- input_range:列的輸入范圍。例如,在上面的例子中,我們使用(1,12),這是月份的范圍;
- width:徑向基函數(shù)的寬度,主要的作用是控制其平滑度
與傅里葉級數(shù)一樣,RBF變量可以用作模型中的解釋變量。
4、季節(jié)性自回歸
自回歸是大多數(shù)預測模型的基礎(chǔ)。這個想法是使用最近的過去觀察(滯后)來預測未來的值。這個概念可以擴展到季節(jié)性模型。季節(jié)性自回歸模型包括同一季節(jié)的過去值作為預測因子。
SARIMA是一種流行的方法,它應用了這個想法:
import pmdarima as pm
model = pm.auto_arima(yt, m=12, trace=True)
model.summary()
# Best model: ARIMA(0,1,0)(1,0,0)[12]利用季節(jié)滯后作為解釋變量是模擬季節(jié)性的有效方法。但是在使用這種方法時,應該處理季節(jié)性單位根。因為非平穩(wěn)的數(shù)據(jù)會產(chǎn)生很多問題。
5、添加額外變量
季節(jié)性虛擬變量或傅立葉級數(shù)等方法都可以捕捉到周期性模式。但是這些方法都是替代性的方法。
我們也可以通過添加額外變量的方式對季節(jié)性進行建模,例如溫度或每個月的工作日數(shù)等外生變量來模擬季節(jié)性。
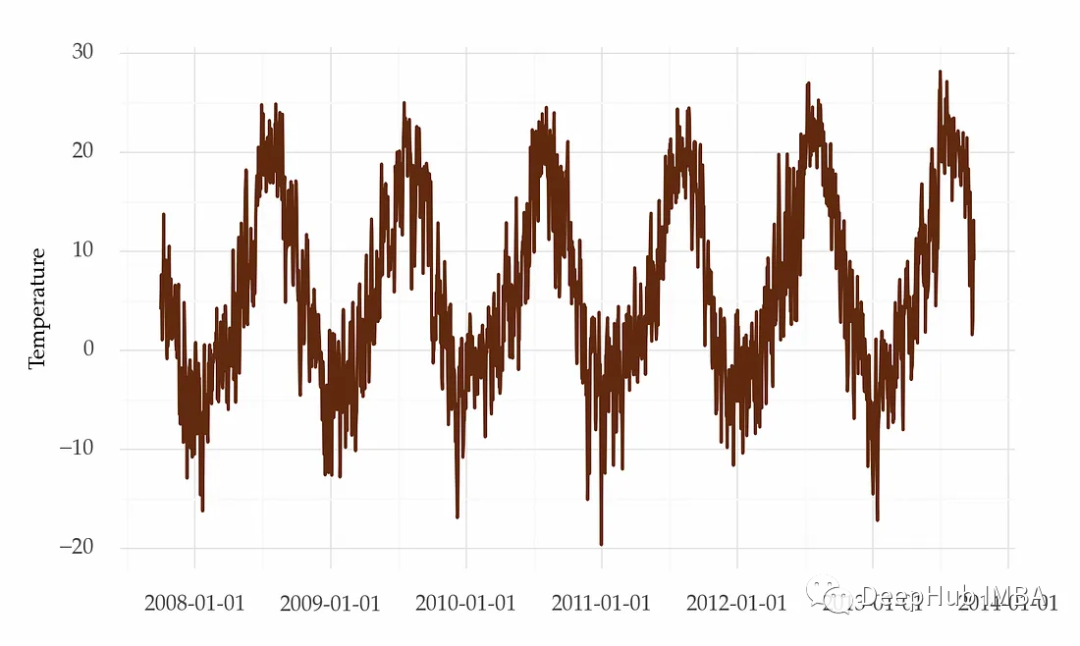
6、季節(jié)性差分
通過在建模之前從數(shù)據(jù)中刪除季節(jié)性來處理季節(jié)性。這種方法叫做季節(jié)差分。
季節(jié)差異是取同一季節(jié)連續(xù)觀測值之間的差異的過程。這種操作對于去除季節(jié)性單位根部特別有用。
可以使用diff方法進行季節(jié)差異:
from sklearn.model_selection import train_test_split
from sktime.forecasting.compose import make_reduction
from sklearn.linear_model import RidgeCV
train, test = train_test_split(yt, test_size=12, shuffle=False)
train_sdiff = train.diff(periods=12)[12:]
forecaster = make_reduction(estimator=RidgeCV(),
strategy='recursive',
window_length=3)
forecaster.fit(train_sdiff)
diff_pred = forecaster.predict(fh=list(range(1, 13)))我們在差分序列上建立了Ridge回歸模型。通過還原差值運算,可以得到原始尺度上的預報。
7、時間序列分解
還可以使用時間序列分解方法(如STL)去除季節(jié)性。
差分和分解的區(qū)別是什么?
差分和分解都用于從時間序列中去除季節(jié)性。但是轉(zhuǎn)換后的數(shù)據(jù)的建模方式不同。
當應用差分時,模型使用差分數(shù)據(jù)。所以需要還原差分操作以獲得原始尺度上的預測。
而使用基于分解的方法,需要兩組預測。一個是季節(jié)性部分,另一個是季節(jié)性調(diào)整后的數(shù)據(jù)。最后的預測是各部分預測的總和。
下面是一個基于分解的方法如何工作的例子:
from statsmodels.tsa.api import STL
from sktime.forecasting.naive import NaiveForecaster
# fitting the seasonal decomposition method
series_decomp = STL(yt, period=period).fit()
# adjusting the data
seas_adj = yt - series_decomp.seasonal
# forecasting the non-seasonal part
forecaster = make_reduction(estimator=RidgeCV(),
strategy='recursive',
window_length=3)
forecaster.fit(seas_adj)
seas_adj_pred = forecaster.predict(fh=list(range(1, 13)))
# forecasting the seasonal part
seas_forecaster = NaiveForecaster(strategy='last', sp=12)
seas_forecaster.fit(series_decomp.seasonal)
seas_preds = seas_forecaster.predict(fh=list(range(1, 13)))
# combining the forecasts
preds = seas_adj_pred + seas_preds在這個例子中,我們建立了一個Ridge 回歸模型來預測經(jīng)季節(jié)調(diào)整后的數(shù)據(jù)。然后將兩個預測加在一起。
8、動態(tài)線性模型(DLM)
回歸模型的參數(shù)通常是靜態(tài)的。它們不隨時間變化,或者是時不變的。DLM是線性回歸的一種特殊情況。其主要特點是參數(shù)隨時間而變化,而不是靜態(tài)的。
dlm假定季節(jié)性時間序列的結(jié)構(gòu)隨季節(jié)而變化。因此合理的方法是建立具有時變參數(shù)的模型。隨季節(jié)變化的參數(shù)。
參考文獻[4]中的書的第15章提供了這種方法的一個簡潔的R示例。他們使用時變的MARSS(多元自回歸狀態(tài)空間)方法來模擬季節(jié)性變化。
總結(jié)
時間序列建模并不是一項簡單的任務,它需要考慮多個因素和技術(shù)。季節(jié)性的存在可以對時間序列數(shù)據(jù)的分析和預測產(chǎn)生重要影響。識別和理解季節(jié)性模式有助于揭示數(shù)據(jù)的周期性變化、制定季節(jié)性調(diào)整策略以及進行更準確的預測。時間序列建模往往需要結(jié)合經(jīng)驗和領(lǐng)域知識,同時靈活運用不同的技術(shù)和方法,以獲得準確、可靠的模型和預測結(jié)果。