時間序列分析和預測在現代數據科學中扮演著關鍵角色，廣泛應用于金融、經濟、氣象學和工程等領域。本文將總結11種經典的時間序列預測方法，并提供它們在Python中的實現示例。

這些方法包括：

1. 自回歸（AR）
2. 移動平均（MA）
3. 自回歸移動平均（ARMA）
4. 自回歸積分移動平均（ARIMA）
5. 季節性自回歸積分移動平均（SARIMA）
6. 具有外生回歸量的季節性自回歸積分移動平均（SARIMAX）
7. 向量自回歸（VAR）
8. 向量自回歸移動平均（VARMA）
9. 具有外生回歸量的向量自回歸移動平均（VARMAX）
10. 簡單指數平滑（SES）
11. Holt-Winters指數平滑（HWES）

本文利用Python的Statsmodels庫實現這些方法。Statsmodels提供了強大而靈活的工具，用于統計建模和計量經濟學分析。

1、自回歸（AR）模型

自回歸（AR）模型是時間序列分析中的基礎模型之一。它假設序列中的每個觀測值都可以表示為其前p個觀測值的線性組合加上一個隨機誤差項。

數學表示

AR(p)模型可以表示為：

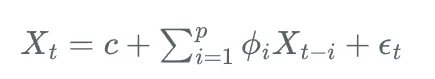
其中，X_t是t時刻的觀測值，c是常數項，\phi_i是自回歸系數，\epsilon_t是白噪聲。

優勢

• 模型簡單，易于理解和實現
• 適用于具有短期依賴性的時間序列
• 計算效率高

局限性

• 假設時間序列是平穩的
• 無法捕捉復雜的非線性模式
• 不適用于具有明顯趨勢或季節性的數據

適用場景

• 金融市場的短期價格波動預測
• 氣象數據的短期預測
• 經濟指標的短期預測

參數解釋

• p：自回歸階數，表示模型考慮的歷史觀測值數量
• 自回歸系數\phi_i：表示過去觀測值對當前值的影響程度

Python實現

from statsmodels.tsa.ar_model import AutoReg
 from random import random
 
 # 生成示例數據
 data = [x + random() for x in range(1, 100)]
 
 # 擬合AR模型
 model = AutoReg(data, lags=1)
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• 自相關函數（ACF）和偏自相關函數（PACF）圖
• AIC（赤池信息準則）和BIC（貝葉斯信息準則）
• 殘差分析：檢查殘差的白噪聲性質

2. 移動平均（MA）模型

移動平均（MA）模型假設時間序列的當前值可以表示為當前和過去的白噪聲誤差項的線性組合。

數學表示

MA(q)模型可以表示為：

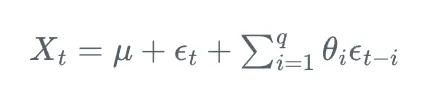
其中，X_t是t時刻的觀測值，\mu是期望值，\theta_i是移動平均系數，\epsilon_t是白噪聲。

優勢

• 適合模擬短期波動
• 可以處理某些非平穩序列
• 對異常值的敏感性較低

局限性

• 無法捕捉長期趨勢
• 參數估計可能較為復雜
• 不適用于具有明顯趨勢或季節性的數據

適用場景

• 金融市場的短期波動分析
• 質量控制中的過程監控
• 信號處理中的噪聲濾除

參數解釋

• q：移動平均階數，表示模型考慮的過去白噪聲誤差項數量
• 移動平均系數\theta_i：表示過去白噪聲誤差對當前值的影響程度

Python實現

from statsmodels.tsa.arima.model import ARIMA
 from random import random
 
 # 生成示例數據
 data = [x + random() for x in range(1, 100)]
 
 # 擬合MA模型
 model = ARIMA(data, order=(0, 0, 1))
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• ACF和PACF圖分析
• 殘差的正態性檢驗
• Ljung-Box測試檢驗殘差的獨立性

3、自回歸移動平均（ARMA）模型

自回歸移動平均（ARMA）模型結合了自回歸（AR）和移動平均（MA）模型的特性，能夠同時捕捉時間序列的自相關性和移動平均特性。

數學表示

ARMA(p,q)模型可以表示為：

其中，X_t是t時刻的觀測值，c是常數項，\phi_i是自回歸系數，\theta_j是移動平均系數，\epsilon_t是白噪聲。

優勢

• 比單純的AR或MA模型更靈活
• 可以描述更復雜的時間序列模式
• 在許多實際應用中表現良好

局限性

• 假設時間序列是平穩的
• 參數估計可能較為復雜
• 可能存在模型識別的困難（選擇合適的p和q值）

適用場景

• 經濟指標預測
• 股票市場分析
• 工業生產過程控制

參數解釋

• p：自回歸項的階數
• q：移動平均項的階數
• 自回歸系數\phi_i和移動平均系數\theta_j：分別表示過去觀測值和過去誤差對當前值的影響程度

Python實現

from statsmodels.tsa.arima.model import ARIMA
 from random import random
 
 # 生成示例數據
 data = [random() for x in range(1, 100)]
 
 # 擬合ARMA模型
 model = ARIMA(data, order=(2, 0, 1))
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• AIC和BIC準則用于模型選擇
• 殘差分析：檢查殘差的白噪聲性質和正態性
• 過擬合測試：比較不同階數模型的性能

4、自回歸積分移動平均（ARIMA）模型

自回歸積分移動平均（ARIMA）模型是ARMA模型的推廣，通過引入差分操作來處理非平穩時間序列。它結合了差分（I）、自回歸（AR）和移動平均（MA）三個組件。

數學表示

ARIMA(p,d,q)模型可以表示為：

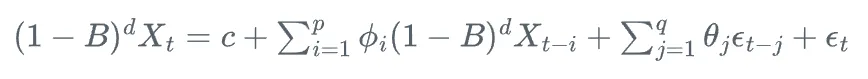
其中，B是后移算子，d是差分階數，其他符號含義與ARMA模型相同。

優勢

• 可以處理非平穩時間序列
• 能夠捕捉復雜的時間序列模式
• 適用于具有趨勢的數據

局限性

• 對異常值敏感
• 可能不適合處理強烈的季節性模式
• 參數選擇可能較為復雜

適用場景

• 經濟和金融數據分析，如GDP增長率預測
• 銷售額預測
• 氣象數據分析

參數解釋

• p：自回歸項的階數
• d：差分階數
• q：移動平均項的階數

Python實現

from statsmodels.tsa.arima.model import ARIMA
 from random import random
 
 # 生成示例數據
 data = [x + random() for x in range(1, 100)]
 
 # 擬合ARIMA模型
 model = ARIMA(data, order=(1, 1, 1))
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data), typ='levels')
 print(yhat)

模型診斷

• 單位根檢驗：確保差分后的序列是平穩的
• ACF和PACF圖分析：輔助確定p和q的值
• 殘差分析：檢查殘差的獨立性和正態性
• 預測性能評估：使用均方根誤差（RMSE）或平均絕對誤差（MAE）等指標

擴展和變體

• 季節性ARIMA（SARIMA）：引入季節性成分
• ARIMAX：包含外生變量的ARIMA模型
• 分數階ARIMA：允許非整數階差分

實施注意事項

• 數據預處理：處理缺失值和異常值
• 模型選擇：使用網格搜索或信息準則（如AIC、BIC）選擇最佳參數
• 模型驗證：使用交叉驗證或滾動預測評估模型性能
• 定期重估：在新數據可用時更新模型參數

ARIMA模型是時間序列分析中最常用和最強大的工具之一。它的靈活性使其能夠適應各種不同類型的時間序列數據，但同時也要求分析者具有豐富的經驗和專業知識來正確指定和解釋模型。在實際應用中，通常需要結合領域知識、統計診斷和試驗來選擇最佳的模型規格。

5、季節性自回歸積分移動平均（SARIMA）模型

季節性自回歸積分移動平均（SARIMA）模型是ARIMA模型的擴展，專門用于處理具有季節性模式的時間序列數據。它在ARIMA模型的基礎上增加了季節性成分。

數學表示

SARIMA(p,d,q)(P,D,Q)m模型可以表示為：

其中，B是后移算子，m是季節性周期，\phi(B)和\theta(B)分別是非季節性AR和MA多項式，\Phi(B^m)和\Theta(B^m)分別是季節性AR和MA多項式。

優勢

• 可以處理具有季節性模式的時間序列
• 能夠捕捉復雜的時間依賴結構
• 適用于多種具有周期性的數據

局限性

• 模型復雜度高，參數估計可能困難
• 需要較長的時間序列才能得到可靠的季節性估計
• 可能對異常值敏感

適用場景

• 季節性銷售數據預測
• 旅游業客流量分析
• 能源消耗預測

參數解釋

• p, d, q：非季節性ARIMA階數
• P, D, Q：季節性ARIMA階數
• m：季節性周期長度

Python實現

from statsmodels.tsa.statespace.sarimax import SARIMAX
 from random import random
 
 # 生成示例數據
 data = [x + random() for x in range(1, 100)]
 
 # 擬合SARIMA模型
 model = SARIMAX(data, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
 model_fit = model.fit(disp=False)
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• 季節性和趨勢分解
• ACF和PACF圖分析（考慮季節性滯后）
• AIC和BIC用于模型選擇
• 殘差分析：檢查季節性殘差的白噪聲性質

6、具有外生回歸量的季節性自回歸積分移動平均（SARIMAX）模型

SARIMAX模型是SARIMA模型的進一步擴展，它允許在模型中包含外生變量（也稱為協變量或回歸量）。這使得模型能夠考慮額外的解釋變量對時間序列的影響。

數學表示

SARIMAX模型可以表示為：

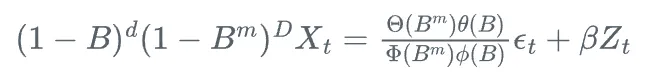
其中，Z_t是外生變量，\beta是相應的系數。

優勢

• 可以納入額外的解釋變量
• 提高預測精度，特別是當外生變量與因變量高度相關時
• 能夠捕捉復雜的時間依賴結構和外部影響

局限性

• 模型復雜度更高，可能面臨過擬合風險
• 需要準確預測外生變量才能進行長期預測
• 參數估計和模型選擇更為復雜

適用場景

• 考慮天氣因素的能源需求預測
• 包含經濟指標的銷售預測
• 考慮多個影響因素的金融市場分析

參數解釋

與SARIMA模型相同，額外包括：

• 外生變量的系數\beta

Python實現

from statsmodels.tsa.statespace.sarimax import SARIMAX
 from random import random
 
 # 生成示例數據
 data1 = [x + random() for x in range(1, 100)]
 data2 = [x + random() for x in range(101, 200)]  # 外生變量
 
 # 擬合SARIMAX模型
 model = SARIMAX(data1, exog=data2, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
 model_fit = model.fit(disp=False)
 
 # 進行預測
 exog2 = [200 + random()]  # 用于預測的外生變量值
 yhat = model_fit.predict(len(data1), len(data1), exog=[exog2])
 print(yhat)

模型診斷

• 外生變量的顯著性檢驗
• 多重共線性檢查
• 預測性能評估：比較包含和不包含外生變量的模型

7. 向量自回歸（VAR）模型

向量自回歸（VAR）模型是用于多變量時間序列分析的統計模型。它將每個變量表示為其自身滯后值和其他變量滯后值的線性函數。

數學表示

VAR(p)模型可以表示為：

其中，Y_t是k維隨機向量，c是k維常數向量，A_i是k×k系數矩陣，\epsilon_t是k維白噪聲向量。

優勢

• 可以捕捉多個變量之間的相互作用
• 允許進行系統的沖擊響應分析
• 適用于預測相互關聯的時間序列

局限性

• 參數數量隨變量數量的增加而迅速增加
• 假設變量之間的關系是線性的
• 可能面臨過度參數化的問題

適用場景

• 宏觀經濟指標分析
• 金融市場不同資產類別之間的相互影響研究
• 多維度銷售數據預測

參數解釋

• p：滯后階數
• k：變量數量
• 系數矩陣A_i：表示不同變量之間的相互影響

Python實現

from statsmodels.tsa.vector_ar.var_model import VAR
 from random import random
 
 # 生成示例多變量數據
 data = list()
 for i in range(100):
     v1 = i + random()
     v2 = v1 + random()
     row = [v1, v2]
     data.append(row)
 
 # 擬合VAR模型
 model = VAR(data)
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.forecast(model_fit.y, steps=1)
 print(yhat)

模型診斷

• Granger因果檢驗：確定變量間的因果關系
• 脈沖響應函數分析：評估一個變量的沖擊對其他變量的影響
• 預測誤差方差分解：分析每個變量對預測誤差的貢獻
• 模型穩定性檢查：確保所有特征根位于單位圓內

VAR模型在多變量時間序列分析中扮演著重要角色，特別是在需要考慮多個相互關聯變量的情況下。它提供了一個系統的框架來分析變量之間的動態相互作用，但同時也要求分析者具有豐富的專業知識來正確指定和解釋模型。在實際應用中，通常需要結合經濟理論、統計診斷和實證分析來選擇最佳的模型規格。

8、向量自回歸移動平均（VARMA）模型

向量自回歸移動平均（VARMA）模型是VAR模型的擴展，它結合了向量自回歸（VAR）和向量移動平均（VMA）的特性，用于分析多變量時間序列數據。

數學表示

VARMA(p,q)模型可以表示為：

其中，Y_t是k維隨機向量，c是k維常數向量，A_i和B_j是k×k系數矩陣，\epsilon_t是k維白噪聲向量。

優勢

• 比VAR模型更靈活，可以捕捉更復雜的動態結構
• 可能比VAR模型更簡潔（在某些情況下）
• 適用于具有移動平均特性的多變量時間序列

局限性

• 參數估計復雜，可能存在識別問題
• 計算成本高，特別是對于高維系統
• 模型選擇和診斷更為復雜

適用場景

• 復雜的經濟系統建模
• 金融市場多資產收益率分析
• 多變量工業過程控制

參數解釋

• p：自回歸階數
• q：移動平均階數
• 系數矩陣A_i和B_j：分別表示自回歸和移動平均部分的影響

Python實現

from statsmodels.tsa.statespace.varmax import VARMAX
 from random import random
 
 # 生成示例多變量數據
 data = list()
 for i in range(100):
     v1 = random()
     v2 = v1 + random()
     row = [v1, v2]
     data.append(row)
 
 # 擬合VARMA模型
 model = VARMAX(data, order=(1, 1))
 model_fit = model.fit(disp=False)
 
 # 進行預測
 yhat = model_fit.forecast()
 print(yhat)

模型診斷

• 多變量Ljung-Box檢驗：檢查殘差的白噪聲性質
• 信息準則（如AIC、BIC）用于模型選擇
• 交叉相關函數（CCF）分析：檢查變量間的相關性

9、具有外生回歸量的向量自回歸移動平均（VARMAX）模型

VARMAX模型是VARMA模型的進一步擴展，它允許在模型中包含外生變量。這使得模型能夠考慮額外的解釋變量對多個相關時間序列的影響。

數學表示

VARMAX(p,q,r)模型可以表示為：

其中，X_t是外生變量向量，C_k是相應的系數矩陣。

優勢

• 可以納入額外的解釋變量，提高預測精度
• 能夠捕捉內生變量和外生變量之間的復雜關系
• 適用于需要考慮外部因素影響的多變量時間序列分析

局限性

• 模型復雜度高，可能面臨過擬合風險
• 需要準確預測外生變量才能進行長期預測
• 參數估計和模型選擇更為復雜

適用場景

• 宏觀經濟預測（考慮政策變量）
• 多產品銷售預測（考慮營銷支出）
• 金融市場分析（考慮多個經濟指標）

參數解釋

與VARMA模型相同，額外包括：

• r：外生變量的滯后階數
• 系數矩陣C_k：表示外生變量對內生變量的影響

Python實現

from statsmodels.tsa.statespace.varmax import VARMAX
 from random import random
 
 # 生成示例多變量數據和外生變量
 data = list()
 exog_data = list()
 for i in range(100):
     v1 = random()
     v2 = v1 + random()
     data.append([v1, v2])
     exog_data.append([i + random()])
 
 # 擬合VARMAX模型
 model = VARMAX(data, exog=exog_data, order=(1, 1))
 model_fit = model.fit(disp=False)
 
 # 進行預測
 exog_forecast = [[100 + random()]]
 yhat = model_fit.forecast(exog=exog_forecast)
 print(yhat)

模型診斷

• 外生變量的顯著性檢驗
• 格蘭杰因果檢驗：檢查外生變量對內生變量的因果關系
• 預測性能評估：比較包含和不包含外生變量的模型

10、簡單指數平滑（SES）模型

簡單指數平滑（SES）是一種基本的時間序列預測方法，它對過去的觀測值賦予指數遞減的權重。這種方法特別適用于沒有明顯趨勢或季節性的數據。

數學表示

SES模型可以表示為：

其中，s_t是t時刻的平滑值，x_t是t時刻的實際觀測值，\alpha是平滑參數（0 < \alpha < 1）。

優勢

• 計算簡單，易于理解和實現
• 對最近的觀測值給予更高的權重
• 適用于短期預測

局限性

• 不適用于具有明顯趨勢或季節性的數據
• 對初始值的選擇敏感
• 可能無法捕捉復雜的時間序列模式

適用場景

• 短期需求預測
• 金融市場短期波動預測
• 穩定性較高的時間序列預測

參數解釋

• \alpha：平滑參數，控制新觀測值的權重

Python實現

from statsmodels.tsa.holtwinters import SimpleExpSmoothing
 from random import random
 
 # 生成示例數據
 data = [x + random() for x in range(1, 100)]
 
 # 擬合SES模型
 model = SimpleExpSmoothing(data)
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• 殘差分析：檢查殘差的隨機性和正態性
• 預測誤差評估：使用MAE、MSE等指標
• 參數穩定性檢查：評估不同\alpha值對預測的影響

11、Holt-Winters指數平滑（HWES）模型

Holt-Winters指數平滑（HWES）模型，也稱為三重指數平滑，是簡單指數平滑的擴展，它可以處理具有趨勢和季節性的時間序列數據。

數學表示

加法Holt-Winters模型的方程：

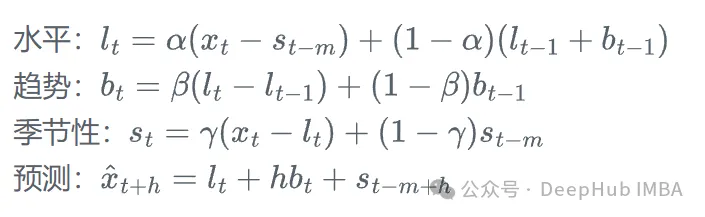
其中，l_t是水平項，b_t是趨勢項，s_t是季節性項，m是季節周期，\alpha、\beta和\gamma是平滑參數。

優勢

• 可以處理具有趨勢和季節性的數據
• 對最近的觀測值給予更高的權重
• 適用于中短期預測

局限性

• 對異常值敏感
• 可能無法捕捉非線性趨勢
• 需要較長的歷史數據來估計季節性成分

適用場景

• 季節性銷售預測
• 能源需求預測
• 旅游業客流量預測

參數解釋

• \alpha：水平平滑參數
• \beta：趨勢平滑參數
• \gamma：季節性平滑參數

Python實現

from statsmodels.tsa.holtwinters import ExponentialSmoothing
 from random import random
 
 # 生成示例數據
 data = [x + 10*sin(x/5) + random() for x in range(1, 100)]
 
 # 擬合Holt-Winters模型
 model = ExponentialSmoothing(data, seasonal_periods=12, trend='add', seasonal='add')
 model_fit = model.fit()
 
 # 進行預測
 yhat = model_fit.predict(len(data), len(data))
 print(yhat)

模型診斷

• 殘差分析：檢查殘差的隨機性、正態性和自相關性
• 預測誤差評估：使用MAE、MAPE等指標
• 參數穩定性檢查：評估不同初始值對預測的影響

模型比較

復雜度遞增

• 最簡單：SES < AR/MA < ARMA < ARIMA
• 中等復雜：SARIMA < SARIMAX
• 最復雜：VAR < VARMA < VARMAX

單變量 vs 多變量

• 單變量模型：AR, MA, ARMA, ARIMA, SARIMA, SARIMAX, SES, HWES
• 多變量模型：VAR, VARMA, VARMAX

處理能力

• 趨勢：ARIMA, SARIMA, SARIMAX, HWES
• 季節性：SARIMA, SARIMAX, HWES
• 外生變量：SARIMAX, VARMAX

計算效率

• 高效：SES, AR, MA
• 中等：ARMA, ARIMA, VAR
• 計算密集：SARIMA, SARIMAX, VARMA, VARMAX

預測范圍

• 短期預測：SES, AR, MA, ARMA
• 中長期預測：ARIMA, SARIMA, VAR, HWES
• 條件長期預測：SARIMAX, VARMAX（依賴外生變量的準確預測）

如何選擇

1. 數據特征分析：

• 平穩性：非平穩數據考慮ARIMA或其變體
• 季節性：存在明顯季節性模式選擇SARIMA或HWES
• 多變量關系：考慮VAR系列模型

2. 預測目標：

• 短期預測：可以考慮較簡單的模型如AR、MA或SES
• 長期預測：ARIMA、SARIMA或VARMAX可能更合適

3. 計算資源：

• 有限資源：優先考慮計算效率高的模型
• 充足資源：可以嘗試更復雜的模型或集成方法

4. 解釋性需求：

• 高解釋性要求：線性模型如AR、ARIMA通常更易解釋
• 性能優先：可以考慮非線性或機器學習方法

5. 外部因素影響：

• 存在已知外部影響因素：考慮SARIMAX或VARMAX

6. 數據量：

• 大數據集：可以考慮更復雜的模型或深度學習方法
• 小數據集：簡單模型如SES或AR可能更穩定

總結

本文詳細介紹了11種經典的時間序列預測方法，從簡單的自回歸模型到復雜的多變量模型。每種方法都有其特定的應用場景和優缺點，沒有一種模型可以適用于所有情況。選擇合適的模型需要考慮數據特征、預測目標、可用資源和領域知識。在實踐中，通常需要嘗試多個模型并比較它們的性能。

時間序列分析是一個廣泛而深入的領域，本文僅涵蓋了其中的一部分內容。隨著機器學習和深度學習技術的發展，如長短期記憶網絡（LSTM）和Prophet等新方法也越來越多地應用于時間序列預測。然而，這些經典方法仍然是時間序列分析的基礎，對于理解更復雜的方法和選擇合適的預測策略至關重要。

在實際應用中，建議嘗試多種方法并比較其性能。同時結合領域知識和數據可視化技術，可以幫助更好地理解數據的特性和選擇合適的預測方法。