超越ToT,蘇黎世理工發布新一代思維圖GoT:推理質量提升62%,成本降低31%
大型語言模型在推理上仍然是弱勢項目,需要依賴各種思維工具輔助完善推理過程。
最近,蘇黎世聯邦理工大學、華沙理工大學的研究人員共同提出了一個全新的LLM思維框架GoT(Graph of Thoughts,GoT),在推理質量和推理速度上都要超越現有的思維鏈(CoT)和思維樹(ToT)等方法。

論文鏈接:https://arxiv.org/pdf/2308.09687.pdf
GoT的關鍵思想和主要優勢在于將LLM生成的信息建模為圖(arbitary graph),其中信息單元(思維,LLM thoughts)作為圖的頂點,頂點之間的依賴關系作為圖的邊。
GoT方法可以將任意的LLM思維組合成協同結果,提取出整個思維網絡的本質,或者使用反饋回路來增強思維。
通過實驗可以證明GoT在不同任務上提供了優于現有技術的優勢,例如,與ToT相比,排序任務的質量提高了62%,同時成本降低了31%
研究人員認為,GoT方法可以讓LLM推理更接近人類的思維和大腦推理機制,比如二者都在內部形成了復雜的網絡結構。
LLM思維(thought)的進化之路
用戶與LLM對話的過程主要包括用戶消息(提示,prompts)和模型回復(思維、想法,thoughts),其中回復可以是一段文本(摘要任務)、一個文檔(生成任務)或是一個代碼塊等。
為了充分激活語言模型的能力,通常會采用各種提示方法:

1. Input-Output (IO) 提示
輸入序列后,直接用語言模型獲取輸出,不添加任何中間思考過程。
2. 思維鏈(Chain-of-Thought, CoT)
在輸入和輸出之間引入多個中間思維狀態,相比IO方法,可以顯著提升語言模型在數學難題和通用推理任務上的性能。
3. 多思維鏈
獨立生成多條思維鏈,然后根據預先指定的評分指標返回最佳輸出結果的思維鏈。
自一致思維鏈(CoT-SC)方法可以將CoT擴展到多條推理路徑,不過沒有進行單路徑內的「局部探索」,例如回溯(backtracking)。
4. 思維樹(Tree of Thoughts, ToT)
ToT將過程或推理建模為一棵思維樹來增強CoT-SC方法,單個樹節點代表部分解決方案;基于給定的節點,思維生成器(thought generator)可以構造出一定數量的新節點,然后用狀態評估器(state evaluator)為每個新節點生成相應評分。
根據用例的不同,可以使用LLM自身對輸出結果進行評估,也可以利用人工評分等。
擴展樹的過程中,節點的調度取決于使用的搜索算法,如深度優先、廣度優先。
其他方法如思維分解(thought decomposition)等或多或少都隱含使用了樹的思路。
思維圖(Graph of Thought, GoT)框架
總體來說,GoT包含四部分:
1. 語言模型推理過程,即在特定上下文中,所有語言模型的思維,以及思維之間的關系
2. 潛在的思維轉換
3. 用于獲取思維評分的評估函數
4. 用于選擇最相關思維的排序函數
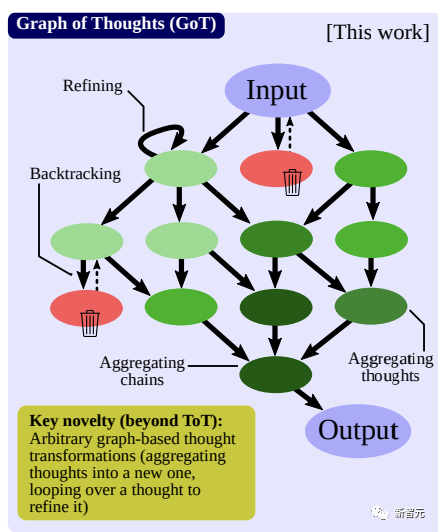
推理過程
研究人員將推理過程建模為一個有向圖,頂點代表某個問題(初始問題、中間問題、最終問題)的一個解決方案,有向邊代表使用「出節點」作為直接輸入構造出的思維(入節點),具體思維的形式取決于用例。
圖節點的類別也不一定相同,例如在生成任務中,某些節點代表「寫一段文字的規劃」,另一些節點用來對「實際文本段」進行建模,推理過程是一個異構圖(heterogeneous graph)。
思維轉換
基于圖結構,GoT可以在推理中實現不同的思維轉換,也可以叫做graph-enabled transformations.
比如說,在寫作任務中,可以將幾篇輸入文章合并成一個連貫的摘要;在排序任務中,可以將幾個排序后的數字子數組(sub-array)合并成一個最終的排序數組。

每次變換操作都包含兩部分:1)反映當前推理狀態的圖,以及2)一個用到的語言模型。
變換操作會修改當前的圖,添加新的節點和輸入邊。
為了最大化GoT的表現力,用戶可以指定要刪除的相應頂點和邊來顯式刪除思維;為了節省上下文空間,用戶可以刪除推理中未來不改進的部分。
1)聚合轉換(Aggregation Transformations)
GoT可以將任意多個思維聚合成一個新的思維,并將不同思維的優勢結合起來。
在最基礎的形式中,只創建一個新的節點,其余思維鏈中的節點作為出節點連接到新節點中。
更一般地,該操作還可以聚合推理路徑,也就是組成更長的推理路徑
2)優化轉換(Refining Transformations)
可以修改當前思維節點v為一條循環邊(v, v),代表與原始思維相同迭代思維。
3)生成轉換(Generation Transformations)
可以基于已有的單思維節點生成一個或多個新的思維,和之前的推理模式,如ToT或CoT-SC類似。
對思維進行評分和排序
評估函數所需要的數據包括受評估的思維、整個推理過程的狀態以及語言模型,要求全推理過程可以最大化函數的通用性。
在對思維的排序時,其輸入包括推理過程、語言模型以及指定返回k個評分最高的思維。
系統架構&可擴展性

GoT架構由一組交互模塊組成:
1. 提示器(Prompter):為LLM準備信息
主要負責把圖結構編碼進提示詞中,GoT架構允許用戶根據不同用例實現不同的圖編碼,提供全部圖結構訪問權限。
2. 解析器(Parser):從LLM的回復中抽取信息
解析器為每個思維構造出一個思維狀態(thought state),包含了抽取出的信息,并用于后續狀態更新。
3. 評分模塊(Scoring):對LLM回復進行驗證和評分
驗證一個給定的LLM思維是否能夠滿足潛在的正確性條件,然后對思維進行打分。
具體分數可能需要構造提示,讓語言模型給出評價;對某些用例來說,人類反饋評分也可以;如果是排序之類的用例,可能還需要引入局部評分函數。
4. 控制器(Controller):協調整個推理過程,并決定如何繼續推理
控制器中包含兩個重要組件:圖操作(the Graph of Operations, GoO)和圖推理狀態(GRS)。
其中GoO是一個靜態結構,指定了給定任務上的圖分解過程,即規定了可用于LLM思維轉換的操作,以及思維之間的順序和依賴關系;每個操作對象都知道自己的前置操作和后繼操作。
GRS是一個動態結構,用來維護LLM推理過程進行中的狀態,包括所有思維的歷史及狀態。

示例用例
1. 排序
比如任務是對有重復的0-9數字序列進行排序,直接輸入的話,語言模型無法對超過一定長度的序列正確排序。

在GoT框架中,研究人員采用基于合并的排序方法:
首先將輸入的數字序列分解為多個子矩陣;然后對子矩陣分別進行排序;再將子矩陣進行排序;最后將所有子矩陣合并,得到最終結果。
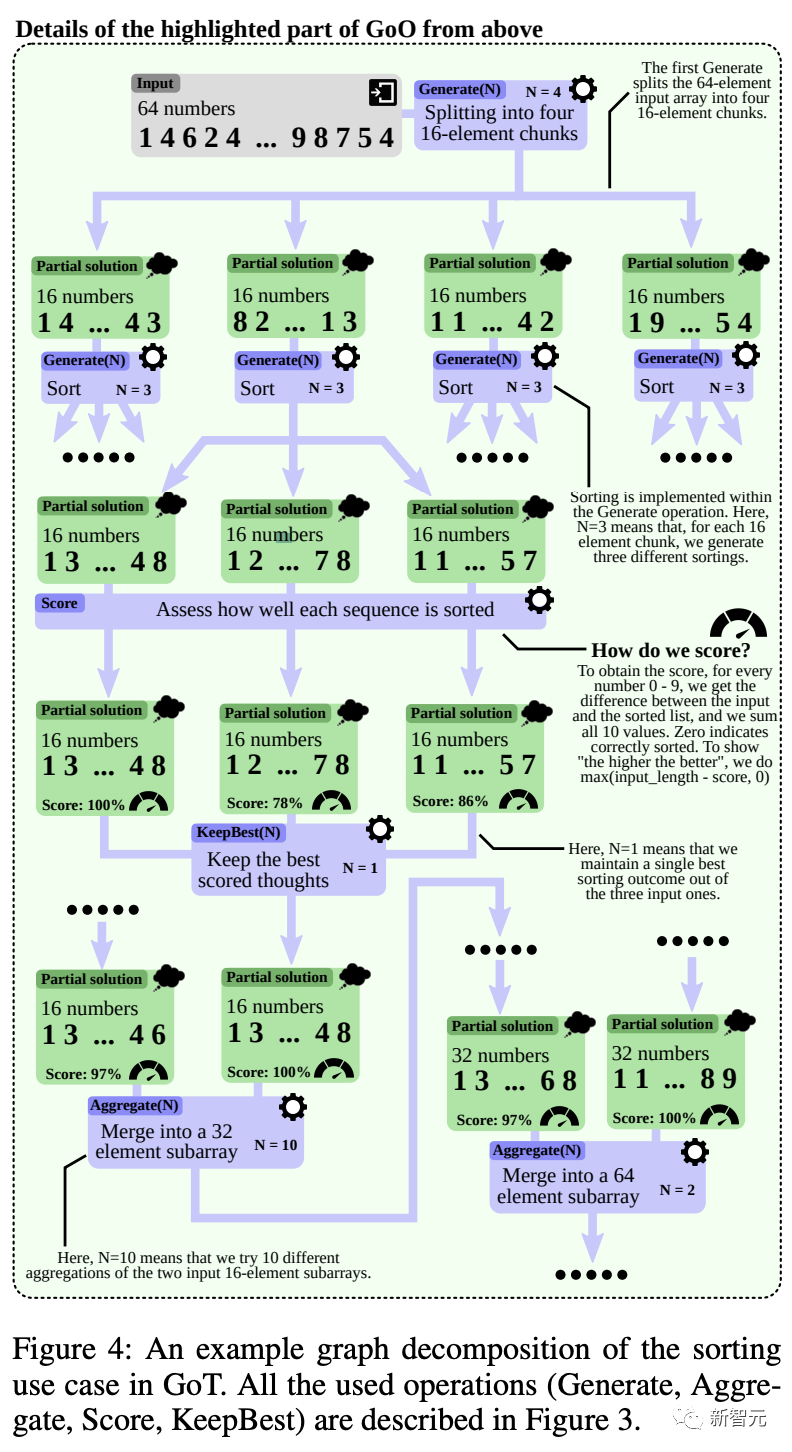
在這個用例中,LLM思維就是一串有序的數字序列。
為了對LLM的輸出進行評分,假定輸入序列a的長度為n,輸出序列b的長度為m,可以將誤差范圍定義為:

X表示錯誤排序的連續數字對的數量,如果相鄰兩個數字排序錯誤,即左邊的數字大于右邊,則X加一。
Y表示,輸出序列中的數字頻率,與輸入序列頻率的吻合程度。
2. 關鍵詞計數任務
GoT框架將輸入文本分割成多個段落,計數每個段落中的關鍵字,并聚合子結果。
段落的數量可以預先定義,也可以留給LLM分割,或者將每個句子視為一個單獨的段落。
為了獲得對思維的評分,首先需要對每個關鍵字推導出計數和正確計數之間的絕對差值,然后將所有差值相加,并得到最終分數。
3. 文檔合并
該任務的目標是基于幾個內容部分重疊的輸入文檔生成一個新的保密協議(NDA)文檔,盡量減少重復,同時最大限度地保留信息,可以廣泛應用于法律程序等領域。
為了給解決方案打分,研究人員要求語言模型查詢兩個值(每個值三次,取平均值),第一個值對應于解決方案冗余(10表示沒有冗余,0表示至少一半的信息是冗余的),第二個值代表信息保留(10表示保留了所有信息,0表示沒有保留),然后計算調和平均值。
延遲與思維量的權衡
GoT在延遲(思維圖中達到給定最終思維的跳數)和思維量(volume,思維圖中存在通往某個思維的路徑數量)之間的權衡,也比之前的提示方案要好。
假設輸出一個思維的時間成本為O(1),每個提示方案的總成本固定為Θ(n):
1. CoT-SC由源自單個起始思維的k個獨立鏈組成;
2. ToT是一個完整的k-ary樹;
3. 在GoT中,在完整k-ary樹的葉子處與一個大小相同但邊反向的鏡像k-ary樹連接起來;
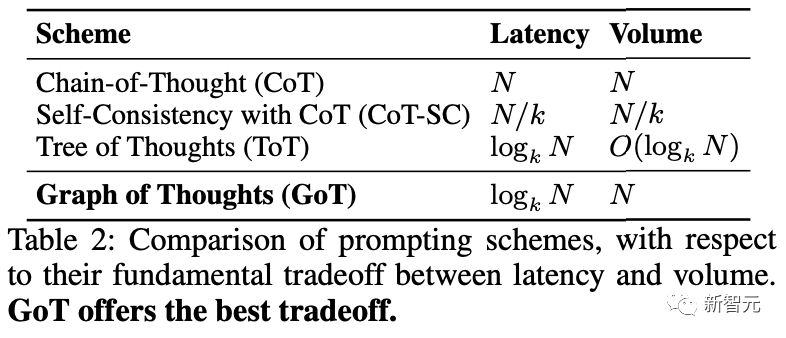
可以看到,雖然CoT-SC提供的思維量為N,但代價是高延遲(N);CoT-SC將延遲降低了k倍(對應于分支因子),但同時也將容量降低了k倍。
ToT提供logk N的延遲,但容量也下降了;
GoT是唯一一個同時具有logk N的低延遲和高容量N的方案,可能是由于GoT利用聚合思想,可以從分解圖中的其他中間思維獲取到最終思維。
實驗結果

總的來說,GoT在排序、找集合交集、關鍵詞計數和文檔合并任務上,其結果質量要比基線模型更好,并且推理成本也更低。
GoT vs. ToT
在所有任務中,GoT都比ToT(樹的分支更多、深度較淺)和ToT2(樹的分支少、深度更深)的性能更好。ToT通常比ToT2的質量更高,但消耗也更大。
相比ToT,GoT方法將中值誤差降低了約62%,從而實現了更高的排序質量,并且運行成本降低了31%以上;優勢主要是因為GoT能夠將復雜的任務分解成更簡單的子任務,獨立解決這些子任務,然后逐步將這些結果合并成最終結果。
GoT vs. IO / CoT
GoT的質量更高,對于排序(P=64)任務,GoT的中值誤差分別比CoT和IO低約65%和約83%,不過GoT和ToT的運行成本遠高于IO和CoT
隨著問題規模P的增加,GoT相比其他基線來說質量提升更大。
總的來說,這個分析說明了GoT確實非常適合復雜的問題案例,因為推理調度通常會隨著問題規模的增長而變得更加復雜。





























