使用高斯混合模型拆分多模態分布
本文介紹如何使用高斯混合模型將一維多模態分布拆分為多個分布。
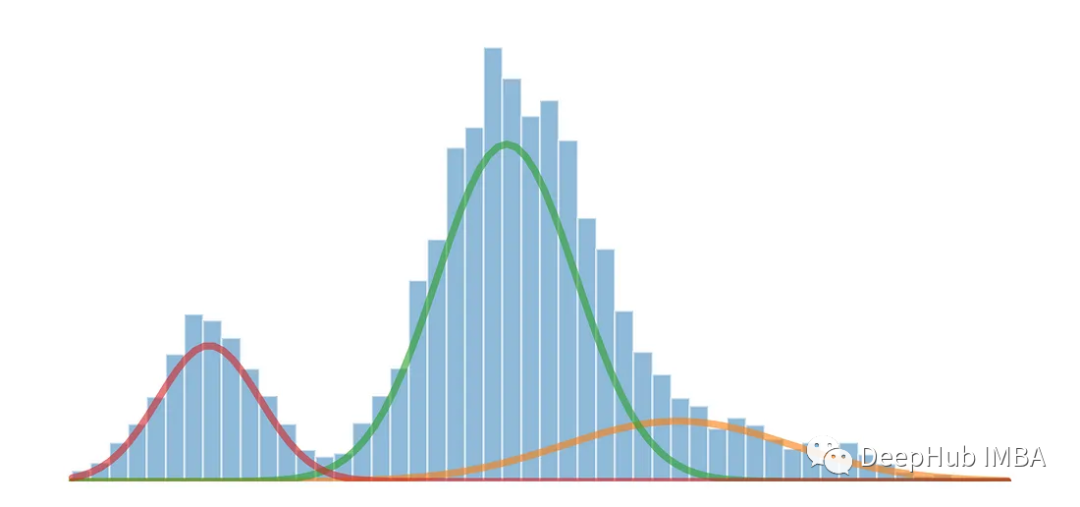
高斯混合模型(Gaussian Mixture Models,簡稱GMM)是一種在統計和機器學習領域中常用的概率模型,用于對復雜數據分布進行建模和分析。GMM 是一種生成模型,它假設觀測數據是由多個高斯分布組合而成的,每個高斯分布稱為一個分量,這些分量通過權重來控制其在數據中的貢獻。
生成具有多模態分布的數據
當一個數據集顯示出多個不同的峰值或模態時,通常會出現顯示出多個不同的峰值或模態,每個模態代表分布中一個突出的數據點簇或集中。這些模式可以看作是數據值更可能出現的高密度區域。
我們將使用numpy生成的一維數組。
import numpy as np
dist_1 = np.random.normal(10, 3, 1000)
dist_2 = np.random.normal(30, 5, 4000)
dist_3 = np.random.normal(45, 6, 500)
multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)讓我們把一維的數據分布形象化。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
plt.hist(multimodal_dist, bins=50, alpha=0.5)
plt.show()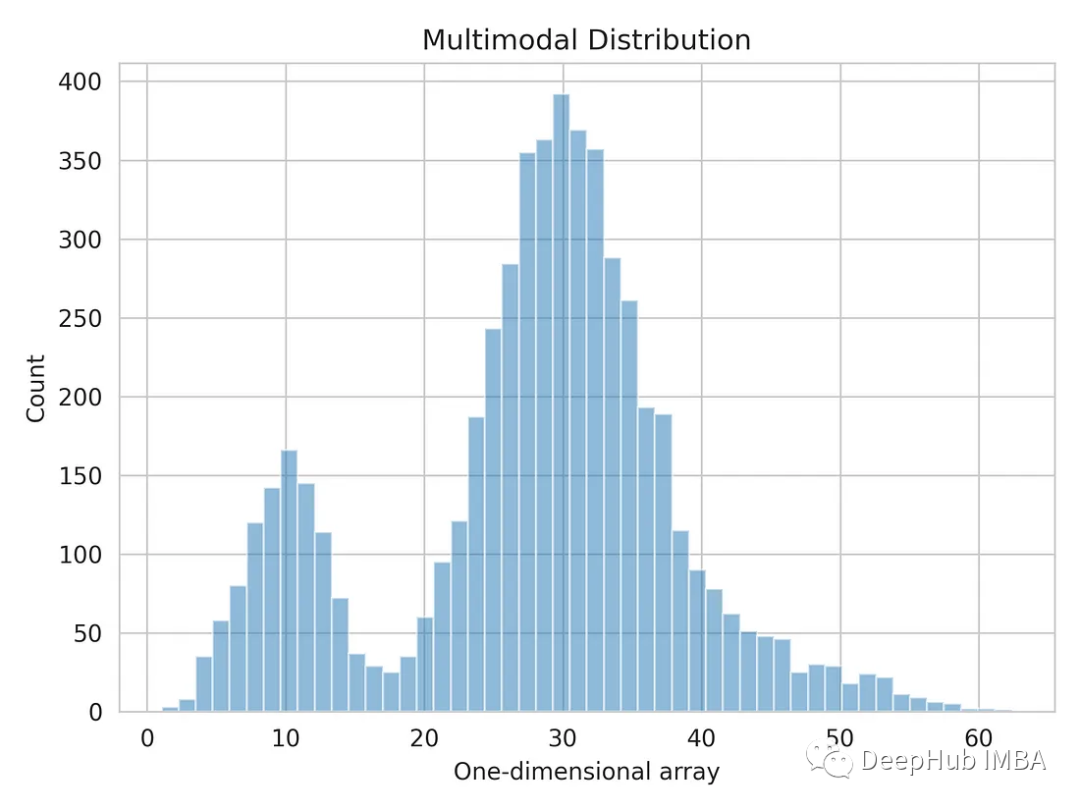
使用高斯混合模型拆分多模態分布
下面我們將通過使用高斯混合模型計算每個分布的均值和標準差,將多模態分布分離回三個原始分布。高斯混合模型是一種可用于數據聚類的概率無監督模型。它使用期望最大化算法估計密度區域。
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_compnotallow=3)
gmm.fit(multimodal_dist.reshape(-1, 1))
means = gmm.means_
# Conver covariance into Standard Deviation
standard_deviations = gmm.covariances_**0.5
# Useful when plotting the distributions later
weights = gmm.weights_
print(f"Means: {means}, Standard Deviations: {standard_deviations}")
#Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]我們已經得到了均值和標準差,可以對原始分布進行建模。可以看到雖然平均值和標準差可能不完全正確,但它們提供了一個接近的估計。
把我們的估計和原始數據比較一下。
from scipy.stats import norm
fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))
for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):
axes[0].hist(dist, bins=bins, alpha=0.5)
axes[1].hist(multimodal_dist, bins=50, alpha=0.5)
x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)
for mean, covariance, weight in zip(means, standard_deviations, weights):
pdf = weight*norm.pdf(x, mean, std)
plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)
plt.show()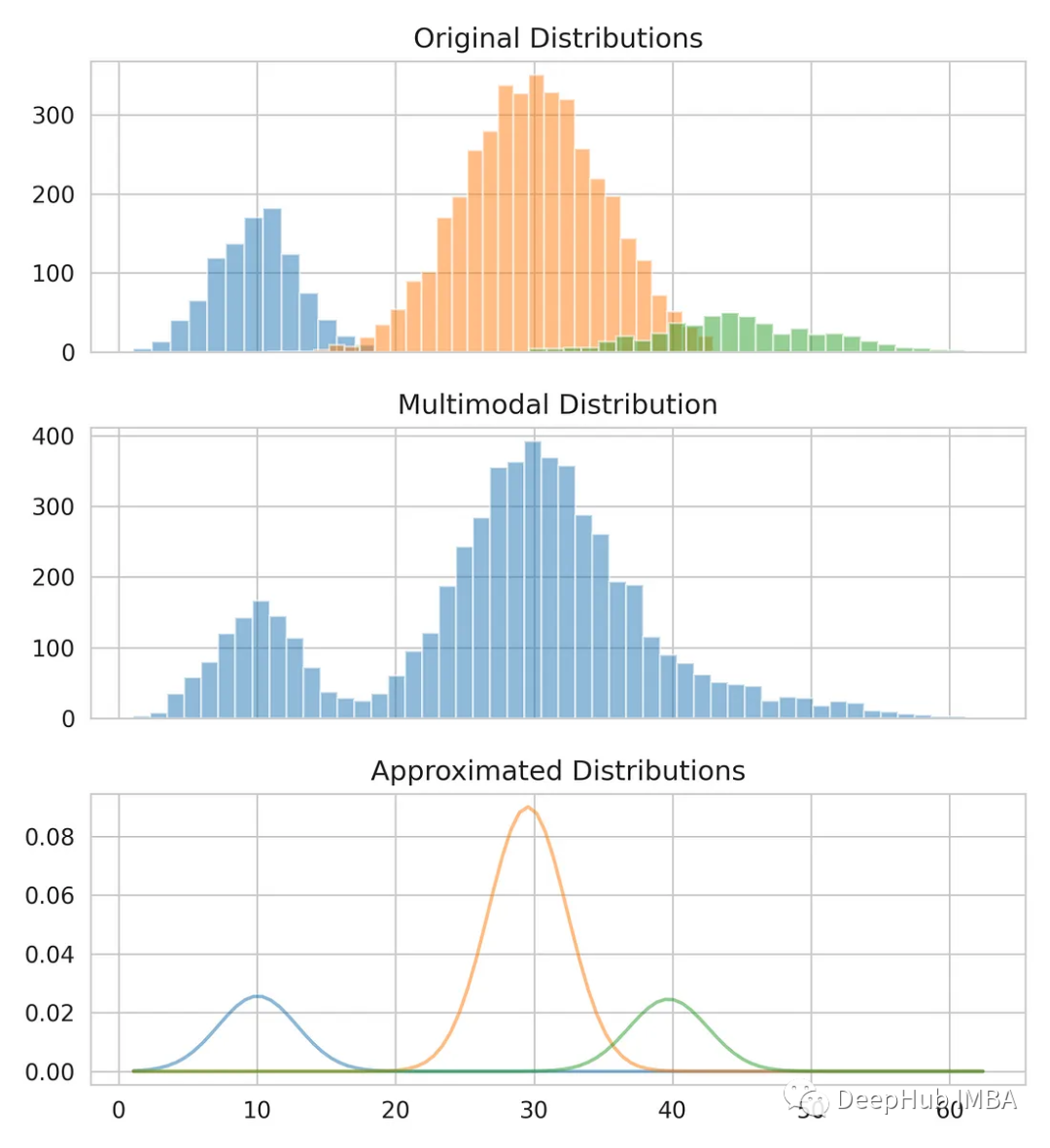
總結
高斯混合模型是一個強大的工具,可以用來對復雜的數據分布進行建模和分析,同時也是許多機器學習算法的基礎之一。它的應用范圍涵蓋了多個領域,能夠解決各種數據建模和分析的問題。
這種方法可以作為一種特征工程技術來估計輸入變量內子分布的置信區間。









































