有了這個代碼模板,合并排序手到擒來
排序在我們的的工程應用中無處不見,也有著非常重要的作用,比如你隨意點開一個搜索引擎,搜索的結構就是經過排序而來。各種電商網站的秒殺活動,用戶點擊秒殺后,服務器會根據用戶的請求時間進行排序。在我們的用的文檔表格中,也存在各種排序。
所以排序真的是無處不見,所以在我們面試中出現排序也不足為奇了。今天就為大家帶來面試中經常出現的一種排序算法,合并排序進行深度解析。
合并排序本質上是一個后續遍歷
合并排序本質上與二叉樹的后序遍歷非常類似的。
首先你還先回憶一下二叉樹的后續遍歷,后序遍歷有個三個重要的特點:
- 拿到子樹的信息;
- 利用子樹的信息;
- 整合出整棵樹的信息。
// 遞歸
function postOrder(root, array = []) {
if (root === null) return null;
postOrder(root.left, array);
postOrder(root.right, array);
array.push(root.val)
}對于合并排序來說,其實也是非常類似:
- 拿到子數組的信息;
- 利用子數組的信息;
- 整合(排序)出整個數組的信息。
簡單利用偽代碼表示就是:
function 后序遍歷/合并排序:
sub = 子結構(子樹/子數組)
full = 整合(sub)不管是后續遍歷,還是合并排序的三個特點,這里可以總結為三個關鍵點:
- 劃分子結構
- 獲取子結構的信息
- 利用子結構的信息整合成一個樹/結果
1. 劃分子結構
對于二叉樹而言,子樹的劃分是天然的,已經在數據結構里面約定好了,比如 Node.left、Node.right。
root.left
root.right
可以直接通過樹的子節點拿但是對于數組而言,在切分的時候,如果想到達最優的效率,那么將數組切為平均的兩半效率應該是最高的。
const mid = begin + ((end - begin)>>1)
數組a = [begin, mid) => 表示左子數組
數組a = [mid, end) => 表示右子數組2. 獲取子結構的信息
對于二叉樹來說,獲取子結構的信息就是或者左右子節點的信息。
postOrder(root.left)
postOrder(root.right)對于合并排序來說,那么就分別需要對左子數組和右子數組進行排序。對子數組的排序,只需要遞歸就可以了。
merge(a, begin, mid)
merge(a, mid, end)3. 整合(排序)出整個數組/樹的信息。
接下來,我們需要將從子結構里面拿到的信息進行加工。不同的需求會導致加工的方式也不太一樣。
對于二叉樹來說,非常簡單,就是將節點值添加到結果中。
array.push(root.val)對于合并排序而言,我們需要將兩個有序的子數組,合并成一個大的有序的數組。
let i = begin;
let j = mid;
let to = begin;
// 將兩個數組合并,判斷條件是,只有左右子數組中還有元素
while(i < mid || j < end) {
// 讀取左數組的元素:
// - 左數組還存在元素并且左數組的開頭元素小于右數組的開頭元素
// - 右數組沒有元素
if ((i < mid && a[i] < a[j]) || j >=end) {
// t 為臨時數組
t[to++] = a[i++];
} else {
// 讀取右數組的元素
t[to++] = a[j++];
}
}最后,不管是二叉樹還是合并排序都要考慮一下邊界:
二叉樹的邊界就是節點不能為空。
if (root === null) return null;合并排序的邊界就是:
- 當 b >= e,說明這個區間是一個空區間,沒有必要再排序;
- 當 b + 1 === e,說明只有一個元素,也沒有必要排序。
if (b > e || b + 1 >= e) {
return
}小結
對于二叉樹來說,代碼相對比較簡單。
function postOrder(root, array = []) {
// 邊界處理
if (root === null) return null;
// 第一步:劃分子結構,二叉樹在結構上已經劃分了子結構 root.left、root.right 可以直接通過樹的子節點拿
// 第二步:獲取子結構信息(遞歸的方式)
postOrder(root.left, array);
postOrder(root.right, array);
// 第三步:整合子結構信息
array.push(root.val)
}對于二叉樹來說,如何切分左右子數組?如何進行合并,合并時注意循環的條件,以及穩定排序的寫法?都是在寫算法時需要注意的。
function merge(a, t, b, e) {
// 邊界處理
if (b > e || b + 1 >= e) {
return
}
/*********************核心代碼****************************/
// 第一步:劃分子結構
const mid = b + ((e-b)>>1);
// 第二步:獲取子結構信息(遞歸的方式)
merge(a, t, b, mid); // 左邊子結構
merge(a, t, mid, e); // 右邊子結構
// 第三步:整合子結構信息
let i = b;
let j = mid;
let to = b;
// 注意:下面是一個很重要的模板????????????
// 將兩個數組合并,判斷條件是,只有左右子數組中還有元素
while(i < mid || j < e) {
// 讀取左數組的元素:
// - 左數組還存在元素并且左數組的開頭元素小于右數組的開頭元素
// - 右數組沒有元素
if ((i < mid && a[i] < a[j]) || j >=e) {
t[to++] = a[i++];
} else {
// 讀取右數組的元素
t[to++] = a[j++];
}
}
/*********************核心代碼****************************/
// 將合并的結果拷貝到源數組中
for (let i = b; i < e; i++) {
a[i] = t[i];
}
}
function mergeSort(nums) {
if (nums === null || nums.length === 0) {
return;
}
merge(nums, [], 0, nums.length)
return nums;
}接著我們利用剛才將的例子來看幾個例子。
例1:排序鏈表
給你鏈表的頭結點 head ,請將其按 升序 排列并返回 排序后的鏈表 。
這道題目就可以套用我們上面提到的模板。
第一步:劃分子結構,對于鏈表來說劃分子結構,也就是找到鏈表的中間節點。鏈表找中間節點也就是利用我上一篇文章中講到的“快慢指針”。
let fast = head,
slaw = head;
// 第一步:劃分子結構,快慢指針,一個節點走一步,另外一個節點走兩步,一快一慢
// 這里 tail 相當于上面數組中的 end,對于鏈表來說,end 也就是 null
while(fast !== tail) {
slaw = slaw.next;
fast = fast.next;
if (fast && fast !== tail) {
fast = fast.next;
}
}
const mid = slaw;第二步:獲取子結構信息(遞歸的方式)。
// 第二步:獲取子結構信息
const list1 = sort(head, mid);
const list2 = sort(mid, tail)第三步:整合信息,有了兩個子結構信息,也就需要將兩個子結構信息合成一個,對于鏈表來說就是合并兩個有序鏈表。這里合并的過程中,還可以用到到我上一篇文章說到的“鏈表第一板斧,假頭”。
// 第三步:整合,合并兩個有序鏈表
var merge = function(head1, head2) {
const dummy = new ListNode();
let tail = dummy;
let list1 = head1;
let list2 = head2;
while(list1 && list2) {
if (list1.val < list2.val) {
tail.next = list1;
tail = list1;
list1 = list1.next;
} else {
tail.next = list2;
tail = list2;
list2 = list2.next;
}
}
if (list1) {
tail.next = list1;
}
if (list2) {
tail.next = list2;
}
return dummy.next;
}最后少不了臨界條件的判斷。
if (head === null) {
return head;
}
if (head.next === tail) {
head.next = null;
return head;
}完整的代碼如下:
var merge = function(head1, head2) {
const dummy = new ListNode();
let tail = dummy;
let list1 = head1;
let list2 = head2;
while(list1 && list2) {
if (list1.val < list2.val) {
tail.next = list1;
tail = list1;
list1 = list1.next;
} else {
tail.next = list2;
tail = list2;
list2 = list2.next;
}
}
if (list1) {
tail.next = list1;
}
if (list2) {
tail.next = list2;
}
return dummy.next;
}
function sort(head, tail) {
if (head === null) {
return head;
}
if (head.next === tail) {
head.next = null;
return head;
}
let fast = head,
slaw = head;
// 第一步:劃分子結構,快慢指針,一個節點走一步,另外一個節點走兩步,一快一慢
// 這里 tail 相當于上面數組中的 end,對于鏈表來說,end 也就是 null
while(fast !== tail) {
slaw = slaw.next;
fast = fast.next;
if (fast && fast !== tail) {
fast = fast.next;
}
}
const mid = slaw;
// 第二步:獲取子結構信息
const list1 = sort(head, mid);
const list2 = sort(mid, tail)
// 第三步:整合,合并兩個有序鏈表
return merge(list1, list2);
}
var sortList = function(head) {
if (head === null || head.next === null) {
return head;
}
return sort(head, null)
};例2:尋找兩個正序數組的中位數
給定兩個大小分別為 m 和 n 的正序(從小到大)數組 nums1 和 nums2。請你找出并返回這兩個正序數組的 中位數 。
算法的時間復雜度應該為 O(log (m+n)) 。
這是一道來自百度的面試題。解法有很多,我們重點介紹基于合并模板的解法。
如果單純的不考慮復雜度,通過合并排序,我們已經能夠將兩個有序的數組合并成一個有序的數組了,再取這個有序數組的中位數。
var findMedianSortedArrays = function(nums1, nums2) {
function merge(a, t, b, e) {
// 邊界處理
if (b > e || b + 1 >= e) {
return
}
/*********************核心代碼****************************/
// 第一步:劃分子結構
const mid = b + ((e-b)>>1);
// 第二步:獲取子結構信息(遞歸的方式)
merge(a, t, b, mid); // 左邊子結構
merge(a, t, mid, e); // 右邊子結構
// 第三步:整合子結構信息
let i = b;
let j = mid;
let to = b;
// 注意:下面是一個很重要的模板????????????
// 將兩個數組合并,判斷條件是,只有左右子數組中還有元素
while(i < mid || j < e) {
// 讀取左數組的元素:
// - 左數組還存在元素并且左數組的開頭元素小于右數組的開頭元素
// - 右數組沒有元素
if ((i < mid && a[i] < a[j]) || j >=e) {
t[to++] = a[i++];
} else {
// 讀取右數組的元素
t[to++] = a[j++];
}
}
/*********************核心代碼****************************/
// 將合并的結果拷貝到源數組中
for (let i = b; i < e; i++) {
a[i] = t[i];
}
}
const nums = [].concat(nums1, nums2);
merge(nums, [], 0, nums.length);
const mid = nums.length>>1;
if (nums.length % 2 === 0) {
return (nums[mid-1] + nums[mid]) / 2;
}
return nums[mid];
};但是這樣操作的話,時間復雜度就變成 O(N),并且空間復雜度也是 O(N)。
如果在面試現場,面試官一定會問你,有沒有更好的辦法?所以我們應該有效地利用兩個數組的有序性解決這道題。下面我會從簡單的情況開始分析。
假設我們有一個一維有序數組,如果我們要拿第 9 小的數。(注:第 1 小就是最小的數。)只需要將前面 8 個數扔掉,然后排在前面的數就是第 9 小的數。
但是現在我們有多個有序數據,怎么辦了?但是非常確認的是,我們如果想拿到第 9 小的數,一定需要丟 8 個數。
那么接下來,思考一下在兩個數組 A,B 中如何扔掉這 8 個數?
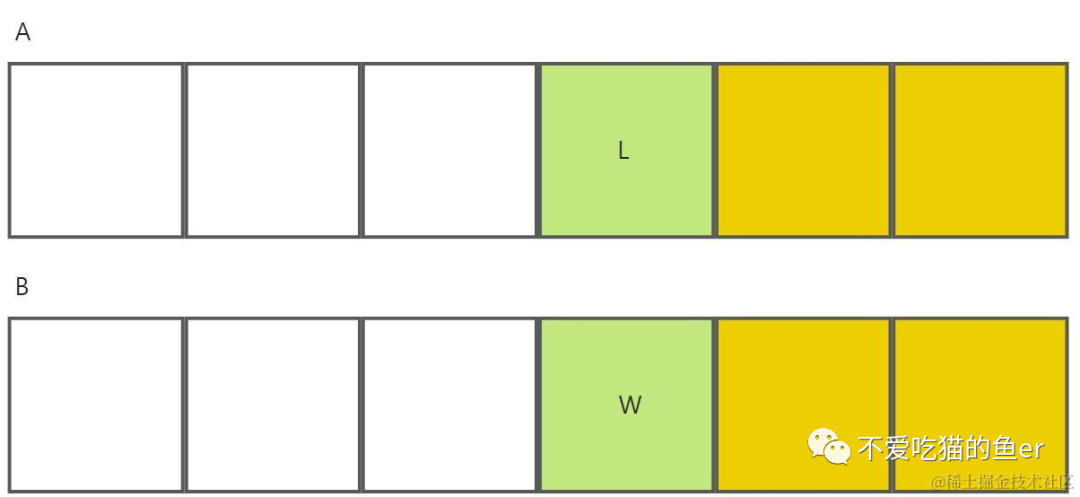
- 要扔掉 4 個數,我們需要看一下兩個數組前 4 個元素(平均分配一下);此時設 A[3] = L,B[3] = W。假設 L >= W,就需要證明:當 L >= W 的時候,[0, W] 都不可能是第 9 小的數,可以扔掉。
 圖片
圖片
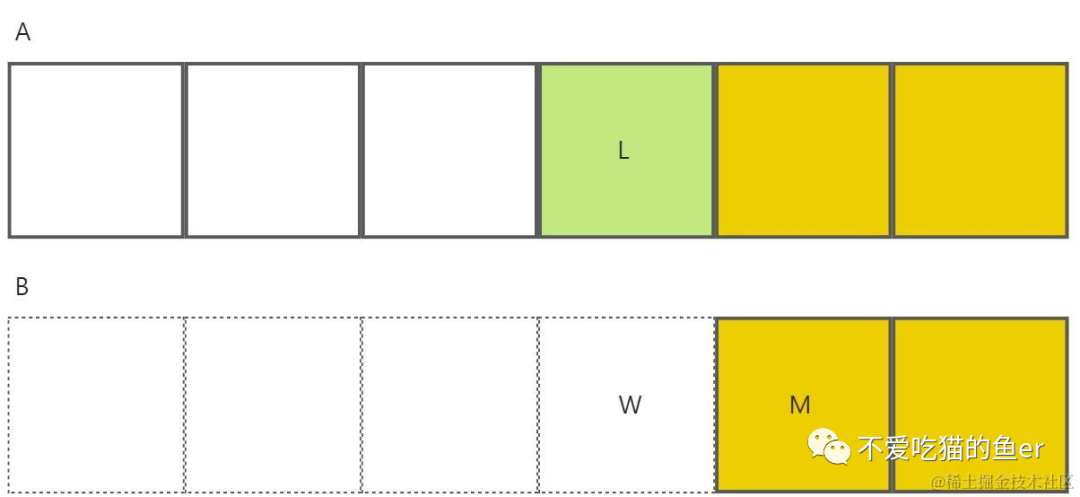
- 當我們扔掉 4 個數之后,兩個有序數組已經變成如下圖所示的樣子,由于我們的目標是扔掉 8 個數,扔掉 4 個數之后,還需要再扔 4 個數。此時我們只需要比較數組開頭的一個元素 A[0], B[M] 的大小,誰小就把誰扔掉。這里我們假設 A[0] 比較小。
 圖片
圖片
- 此時還剩下 3 個數需要扔掉,那么按照上面的方式在進行丟棄就行。
所以總結一下,當我們需要丟棄 K 個元素的時候。k 是偶數的時候,我們只需要比較 A[k/2-1] 和 B[k/2-1] 的大小,誰小就扔掉對應的 [0...k/2-1] 這一段;k 是奇數的時候,我們只需要比較 A[k/2] 和 B[k/2] 的大小,誰小就扔掉對應的 [0...k/2] 這一段。不過由于整數在程序中的整除特性,我們可以將奇數和偶數的情況統一起來。需要扔掉 k 個數的時候,p = (k-1)/ 2,你只需要比較 A[p] 和 B[p] 的大小即可。如果 A[p] >= B[p],那么就可以把 B[0....p] 這段都扔掉。
var findMedianSortedArrays = function(A, B) {
let len = A.length + B.length;
let alen = A.length, blen = B.length;
let i = 0, j = 0;
// 如果兩個數組的總長度為0
//那么不用再找了,肯定是沒有中位數的,這里直接返回一個0
if (len == 0) {
return 0;
}
// 總長度為偶數的情況:
// 如果有4個數,那么當扔掉1個數之后
// 接下來需要合并的兩個數排[2,3]就是中位數
// 總長度為奇數的情況:
// 比如如果有5個數,那么當合并掉2個數之后
// 接下來的那個排[3]位的就是中位數。
// 所以這里k表示:要扔掉的數的個數
// 第一步:劃分子結構
let k = (len - 1) >> 1;
// 第二步:找到子結構信息
while (k > 0) {
// 我們需要比較A[p]與B[p]
// 只不過當數組的起始位置是i和j的時候。
// 比較的元素就變成 A[i+p], B[j+p]
let p = (k - 1) >> 1;
// 這時直接比較A[i + p]和B[j+p]來決定誰可以被扔掉掉
// 注意這里扔掉的時候,只需要前移p + 1即可。
if (j + p >= blen || (i + p < alen && A[i + p] < B[j + p])) {
i += p + 1;
} else {
j += p + 1;
}
k -= p + 1;
}
// 第三步:整合信息
// 把排在前面的數取出來
let front =
(j >= blen || (i < alen && A[i] < B[j])) ? A[i++] : B[j++];
// 如果總長度為奇數,那么這個時候,front就是我們要找的中位數
if ((len & 1) == 1) {
return front;
}
// 此時總的數目為偶數,那么需要再取一個數,求平均值。
let back =
(j >= blen || (i < alen && A[i] < B[j])) ? A[i] : B[j];
return (front + back) / 2.0;
};一共要合并的長度可以認為是 N/2,然后每次取一半進行合并。因此,合并次數為 O(lgN),空間復雜度為 O(1)。
總結
通過合并排序,可以將兩個有序的數組合并成一個有序的數組了。合并是一個非常經典的模板代碼,你一定要理解并且背下來,很多地方都會用。比如合并有序鏈表,合并數組。一個小小的合并模板可就以解決這么多問題,多積累模版可以幫助我們在面試中快速答題。

































