如何回溯解決組合問題和字符串分割
天氣漸寒,大家做好保暖措施。反正我在武漢是被凍傻了??。
首先,做任何有關回溯的題,一定要把這個遞歸函數模板記在心里!!
void backtracking(參數) {
if (終止條件) {
存放結果;
return;
}
for (選擇本層集合中元素(畫成樹,就是樹節點孩子的大小)){
處理節點;
backtracking();
回溯,撤銷處理結果;
}
}組合總和問題
LeetCode 39:給你一個無重復元素的整數數組candidates和一個目標整數 target ,找出 candidates 中可以使數字和為目標數 target 的 所有不同組合 ,并以列表形式返回。你可以按任意順序返回這些組合。candidates 中的 同一個 數字可以 無限制重復被選取 。如果至少一個數字的被選數量不同,則兩種組合是不同的。數組中的元素滿足1 <= candidates[i] <= 200。
示例:
- 輸入:candidates = [2,3,6,7],target = 7
- 輸出:[[2,2,3],[7]]
- 解釋:2 和 3 可以形成一組候選,2 + 2 + 3 = 7 。注意2可以使用多次。7 也是一個候選, 7 = 7 ,僅有這兩種組合。
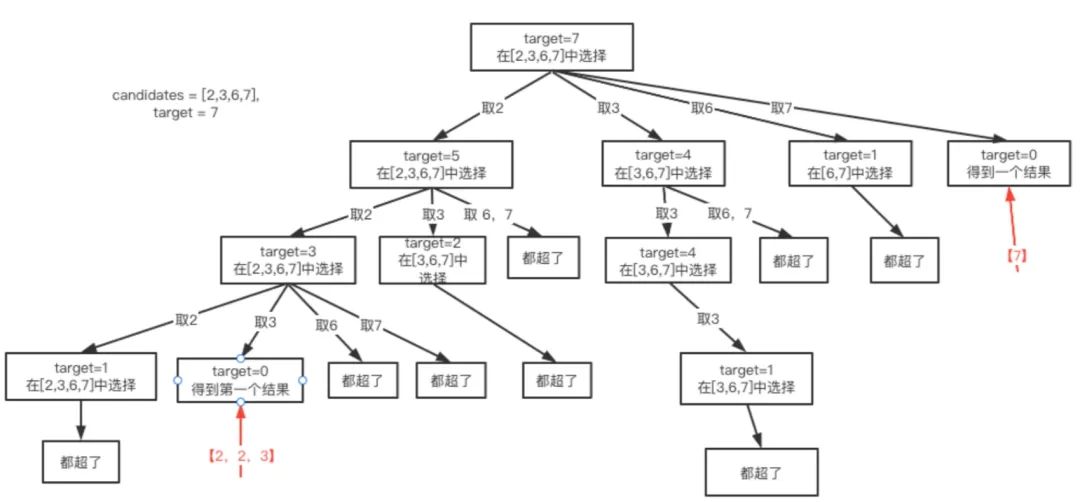
分析:首先,對于序列{2,3,6,7},target=7。可以先選2,然后剩下的target就是7-2=5。再選一個2,剩余5-2=3。之后再選一個2,剩余3-2=1。已經小于2了,我們不能繼續向下了,要撤回一下,看有沒有3。有3,就得到了第一個結果{2,2,3}。
然后,撤回到只選了一個2的時候,這時不能再取2了,而是從{3,6,7}中選擇,如下圖所示,沒有符合要求的!以此類推,后面嘗試從3、6和7開始選擇。
 圖片
圖片
所以我們最終得到的結果就是{2,2,3}和{2,5}。
這個圖橫向是針對每個元素的暴力枚舉,縱向是遞歸,也是一個縱橫問題。
List<List<Integer>> res = new ArrayList<>(); //結果數組
List<Integer> path = new ArrayList<>(); //記錄當前正在訪問的路徑
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates,0,target);
return res;
}
public void dfs(int[] c,int u,int target){
if(target < 0) return;
if(target == 0){
res.add(new ArrayList(path));
return;
}
for(int i = u ; i < c.length;i++){
if(c[i] <= target){
path.add(c[i]);
dfs(c,i,target-c[i]);
path.remove(path.size() - 1);
}
}
}配合上文提到的回溯模板你就會發現,這簡直就是標準的回溯題目。
分割字符串
LeetCode 131:給你一個字符串 s,請你將 s 分割成一些子串,使每個子串都是回文串。返回 s 所有可能的分割方案。
示例 1:
- 輸入:s = "aab"
- 輸出:[["a","a","b"],["aa","b"]]
示例 2:
- 輸入:s = "a"
- 輸出:[["a"]]
分析:每個子串都要是回文串,這個功能可以單獨寫一個函數用于判斷一個字符串是不是回文串。那么這個函數怎么實現呢?很簡單,利用雙指針分別指向字符串的首尾,一起往中間遍歷,一旦相同位置上的字符不相同就返回false,否則就默認返回true。
還要再解決一個問題:如何分割?
 圖片
圖片
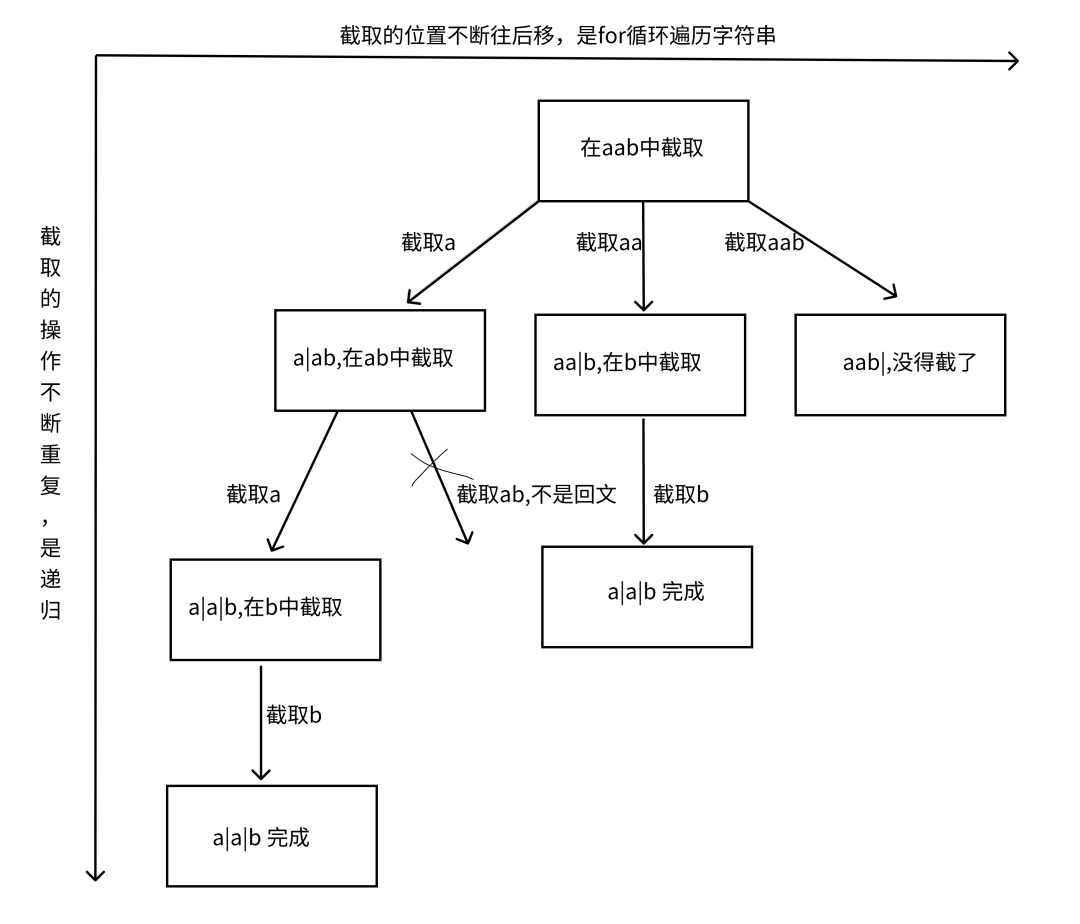
上圖中,劃豎線分開的就是每次分出的子串,右邊就是還沒分的。可見每次分出一個的時候我們都要判斷一下是不是回文。
第一次切'a',第二次切'aa',第三次切'aab'。這對應的就是回溯里的for循環,也就是橫向方面。第一次切了'a',剩下的就是'ab'。遞歸就是再將其再切一個回文下來,也就是第二個'a',剩下的'b'再交給遞歸進一步切割。這就是縱向方面要干的事情,其他以此類推。
用一個二維數組lists保存最后的結果。回想我們回溯的模板。首先想明白他的終止條件是什么?答:整個字符串都遍歷完之后。for循環就是圖中橫向的那一部分。回溯,就是處理完這種方案之后,退回的第一層,開始下一種分割方案。
List<List<String>> lists = new ArrayList<>();
Deque<String> deque = new LinkedList<>();
public List<List<String>> partition(String s) {
backTracking(s, 0);
return lists;
}
private void backTracking(String s, int startIndex) {
//如果起始位置大于s的大小,說明找到了一組分割方案
if(startIndex >= s.length()){
lists.add(new ArrayList(deque));
return;
}
for(int i = startIndex;i < s.length();i++){
if(isPalindrome(s,startIndex,i)){
String str = s.substring(startIndex,i+1);
deque.addLast(str);
}else{
continue;
}
//起始位置后移,保證不重復
backTracking(s,i+1);
deque.removeLast();
}
}
private boolean isPalindrome(String s,int startIndex,int end){
for(int i = startIndex, j = end;i < j;i++ , j--){
if(s.charAt(i) != s.charAt(j)){
return false;
}
}
return true;
}看到這你依舊是蒙蒙?沒事,俺也一樣!(抱拳)這在力扣上都會被懷疑是不是困難題啊哈哈哈哈。
 圖片
圖片
沒事沒事,我第一次的時候調代碼就調了半天,很正常,我一點事都沒有??。



























