打破信息差!一款讓人驚艷的大模型3D可視化工具!
近日,一位來自新西蘭的小哥Brendan Bycroft在技術圈掀起了一股熱潮。他創作的一項名為大模型3D可視化的項目,不僅登上了Hacker News的榜首,而且其震撼的效果更是讓人瞠目結舌。通過這個項目,你將在短短幾秒鐘內完全理解LLM(Large Language Model)的工作原理。
無論你是否是技術愛好者,這個項目都將給你帶來前所未有的視覺盛宴和認知啟迪。讓我們一起來探索這個令人驚嘆的創作吧!
簡介
本項目中,Bycroft詳細解析了OpenAI科學家Andrej Karpathy開發的一款輕量級GPT模型,名為Nano-GPT。作為一個縮小版的GPT模型,該模型僅擁有85000個參數。 當然,盡管這個模型比OpenAI的GPT-3或GPT-4小得多,但可謂是“麻雀雖小,五臟俱全”。
Nano-GPT GitHub:https://github.com/karpathy/nanoGPT
為了方便演示Transformer模型每一層,Bycroft為Nano-GPT模型安排了一個非常簡單的目標任務:模型輸入是6個字母"CBABBC",輸出是按字母順序排好的序列,例如輸出 "ABBBCC".
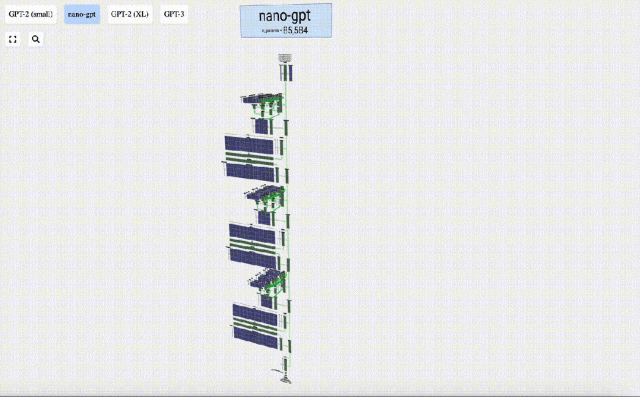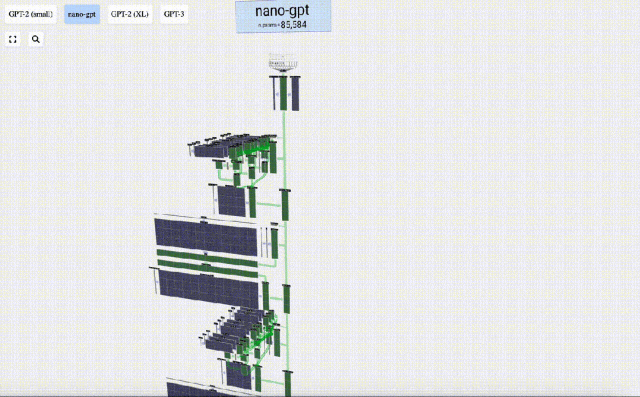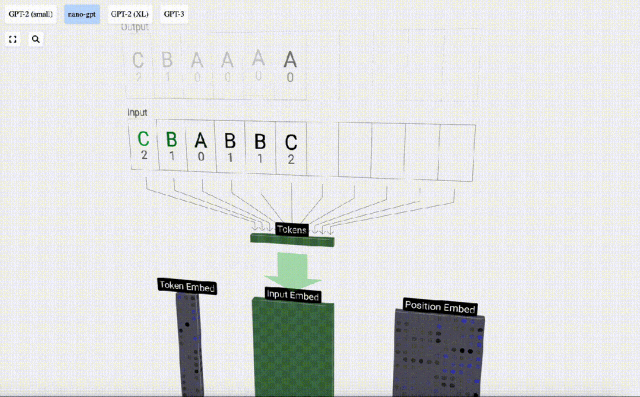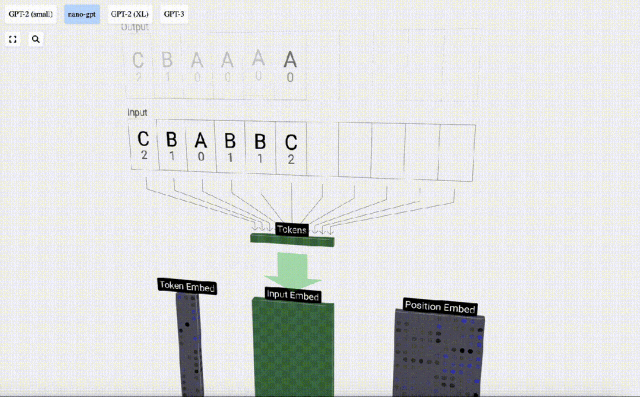
我們稱每個字母為token,這些不同的字母構成了詞表 vocabulary:
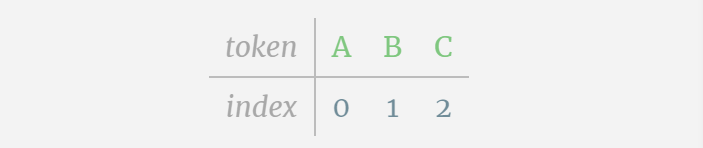
對于這張表格來說,每個字母分別分配了一個下標token index。 這些下標組成的序列可以作為模型的輸入:2 1 0 1 1 2
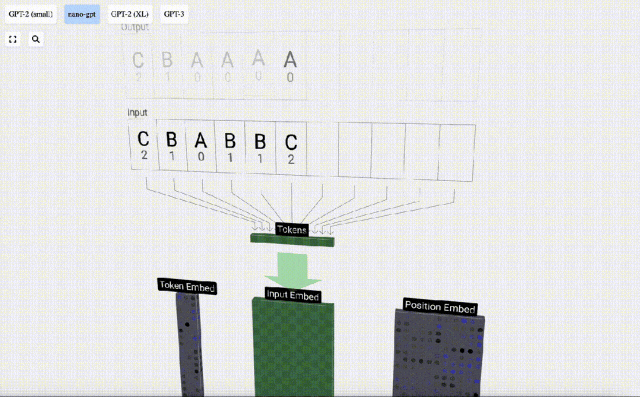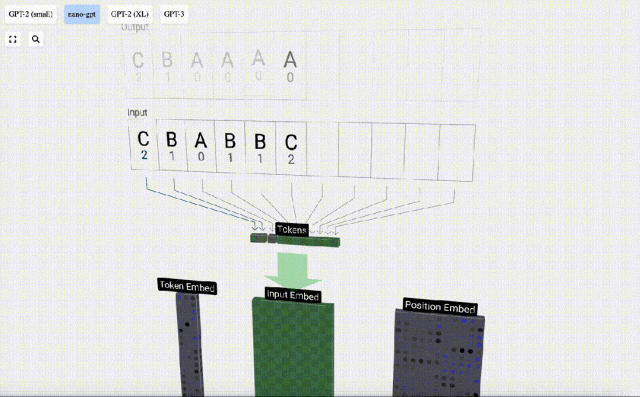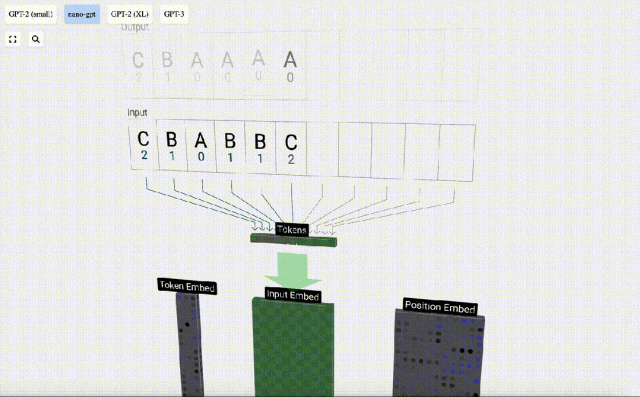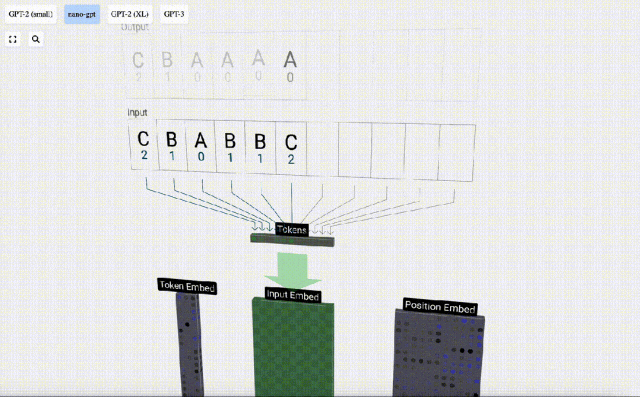
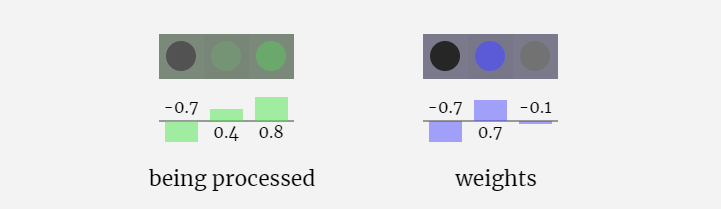
3D可視化中,每個綠色的單元代表經過計算的數字,而每個藍色的單元則表示模型的權重。
序列處理中,每個數字首先會被轉換為一個C維的向量,這個過程稱為嵌入(embedding)。在Nano-GPT中,這個嵌入的維度通常為48維。通過這種嵌入操作,每個數字被表示為一個在C維空間中的向量,從而能夠更好地進行后續的處理和分析。
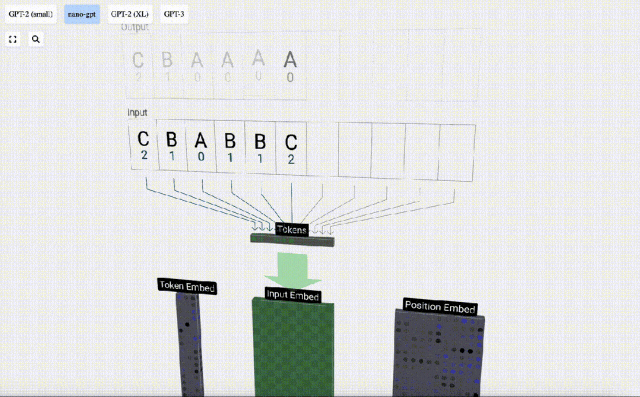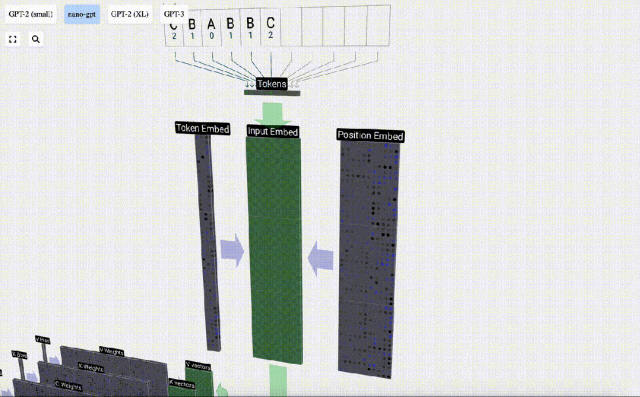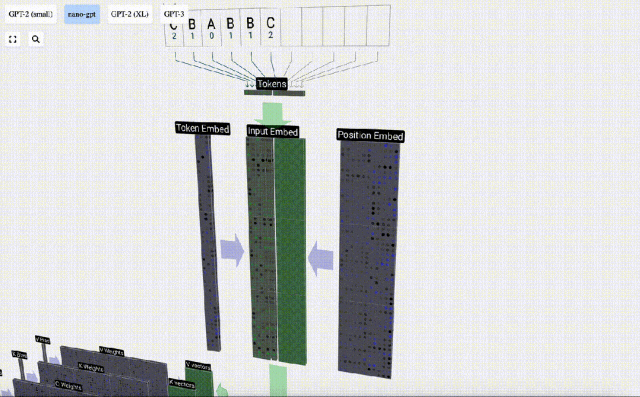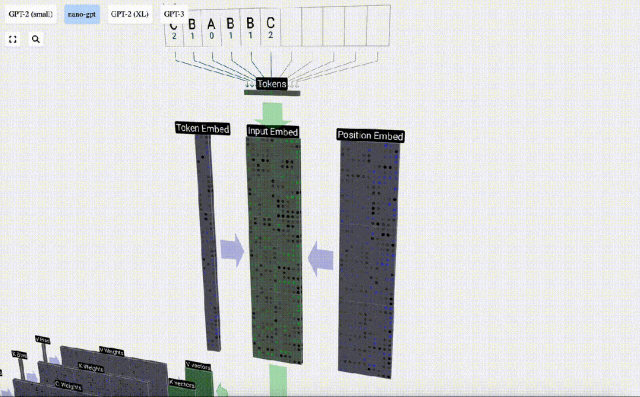
embedding要經過一系列中間的模型層計算,這中間的模型層一般稱為Transformers,最后到達底層。

「那么輸出是什么呢?」
模型的輸出是序列的下一個token。 所以在最后,我們得到了下一個token是A B C的概率值。
在這個例子里,第6個位置模型以較大概率輸出了A。現在我們可以將A作為輸入傳入模型,重復整個過程就可以了。
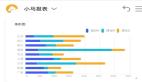
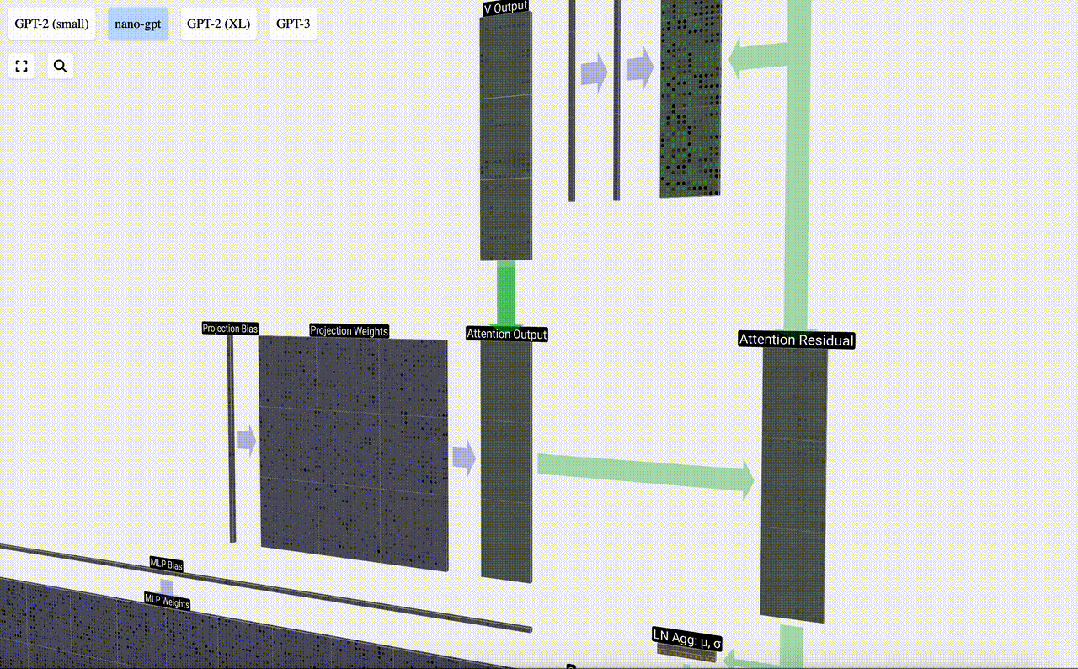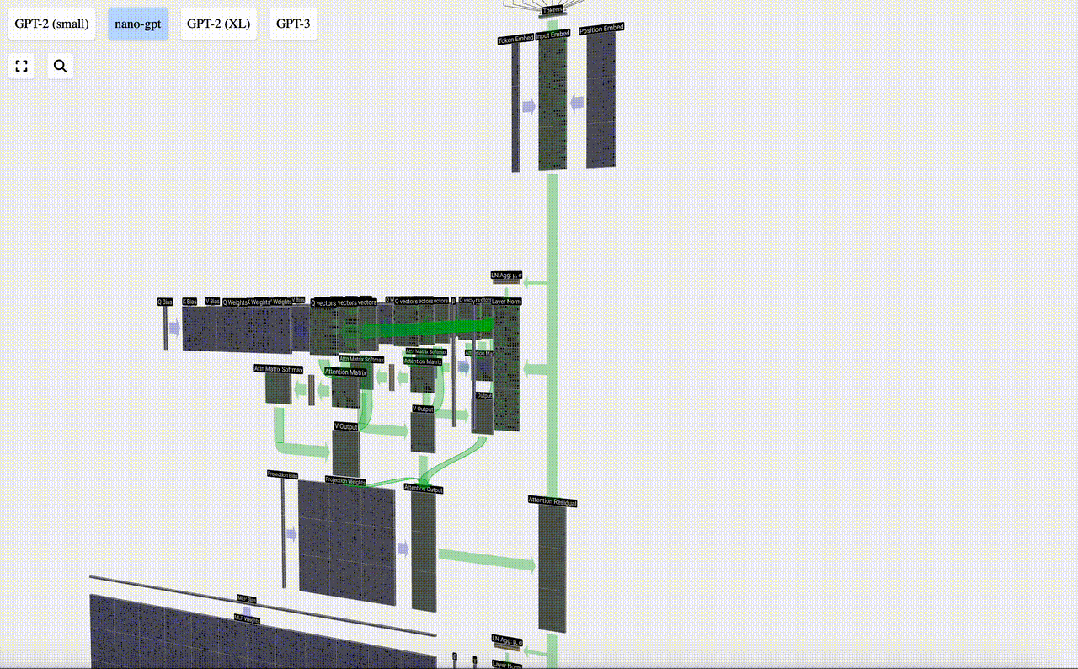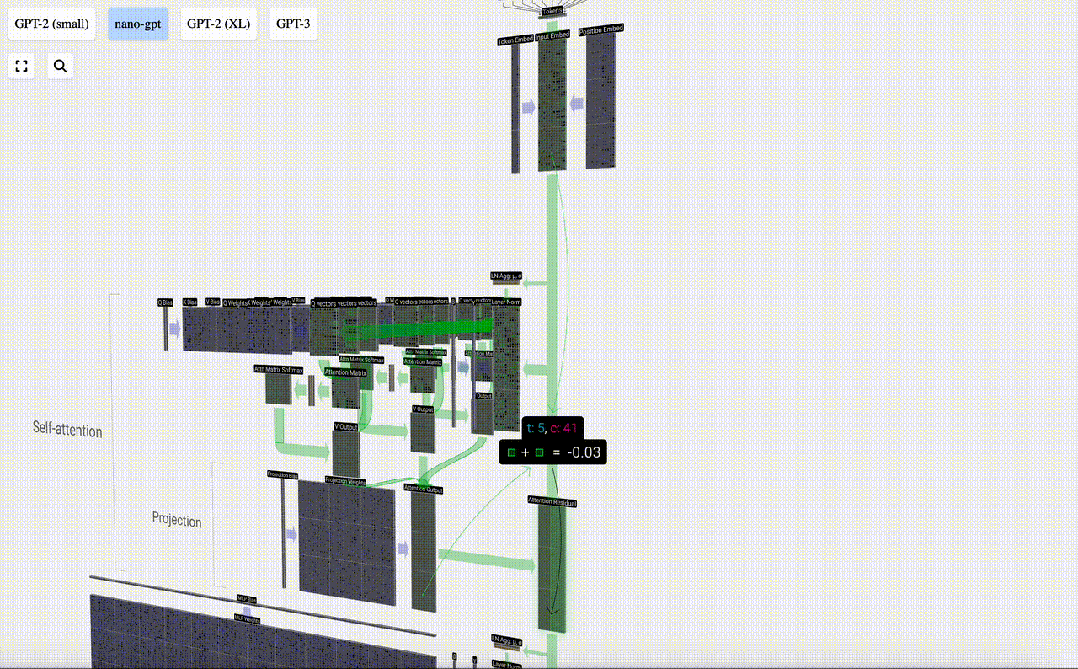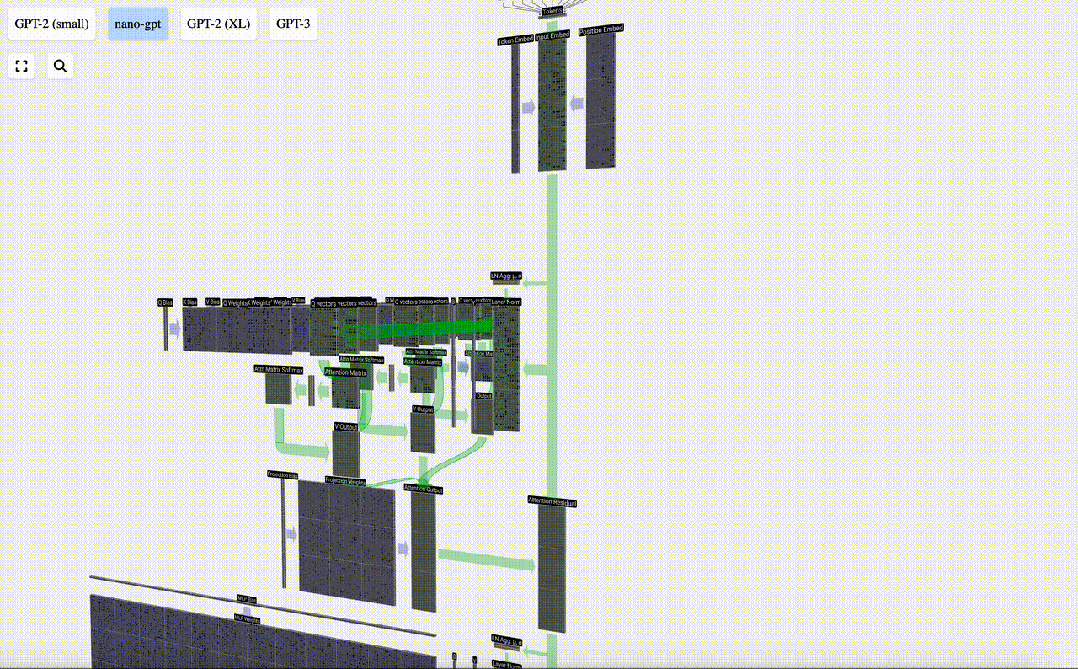
此外還展示了GPT-2和GPT-3可視化效果。
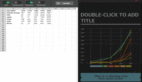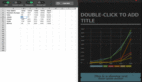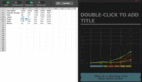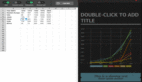
- GPT-3具有1750億個參數,模型層足足有8列,密密麻麻沒遍布了整個屏幕。
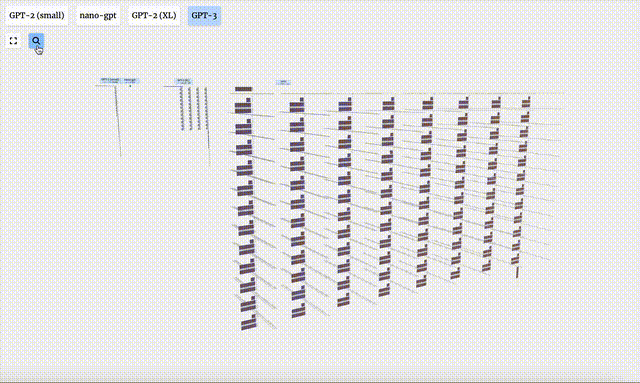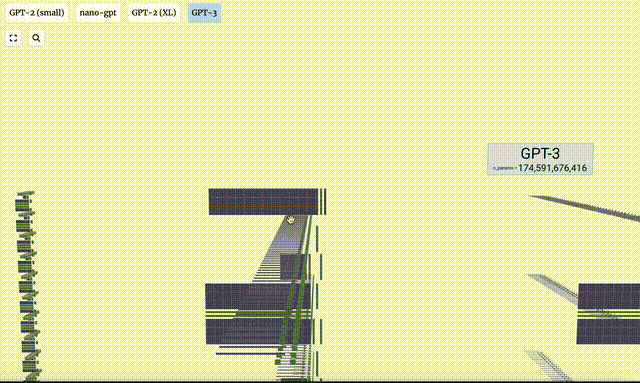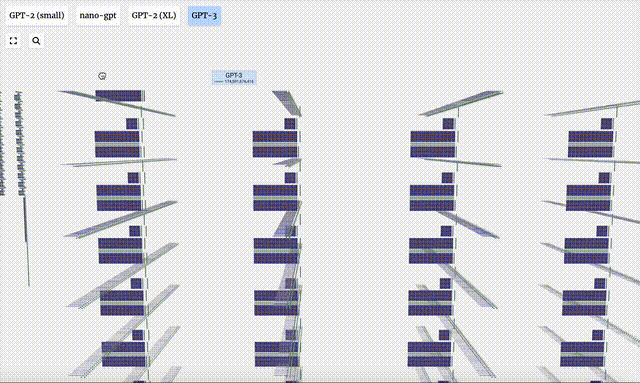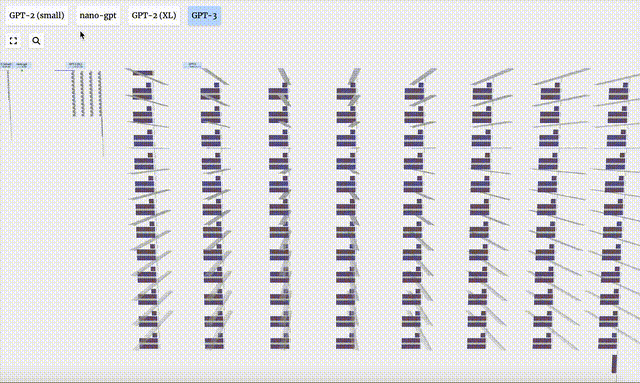
- GPT-2模型的不同參數版本展現出了巨大的架構差異。這里以GPT-2(XL)的150億參數和GPT-2(Small)的1.24億參數為例。

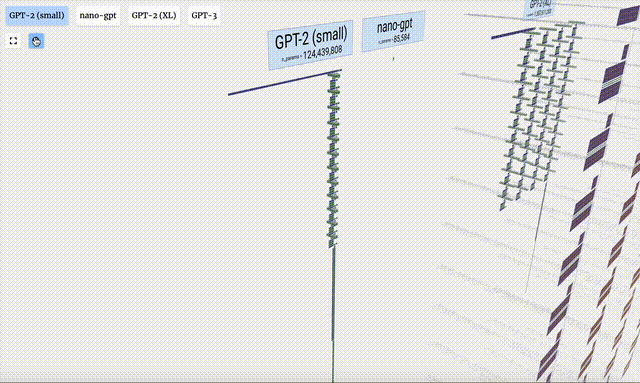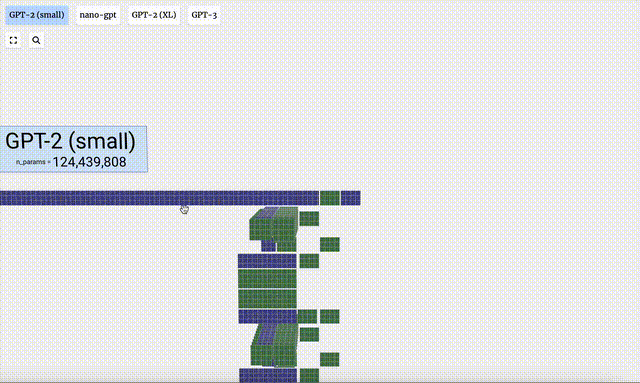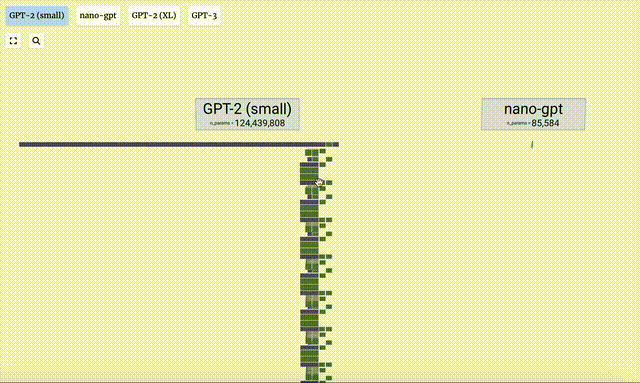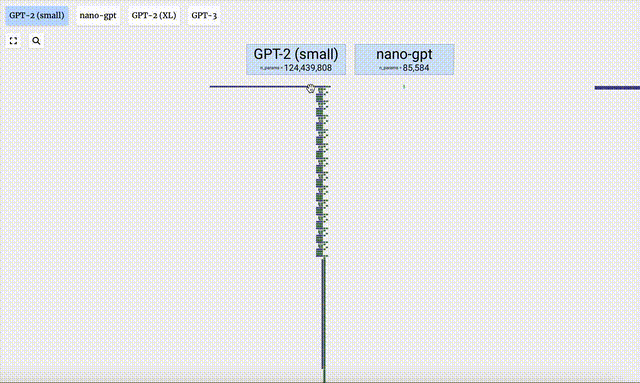
需要注意的是,本可視化主要是側重于模型推理(inference),而不是訓練,因此它只是整個機器學習過程的一小部分。并且,這里假設模型的權重已經經過預訓練,再使用模型推理來生成輸出。
嵌入Embedding
前面有提到,如何使用一個簡單的查找表(Lookup Table)將token映射為一串整數。
這些整數,即標記token index,這是模型中第一次也是唯一一次看到整數。之后,將使用浮點數(十進制數)進行運算。
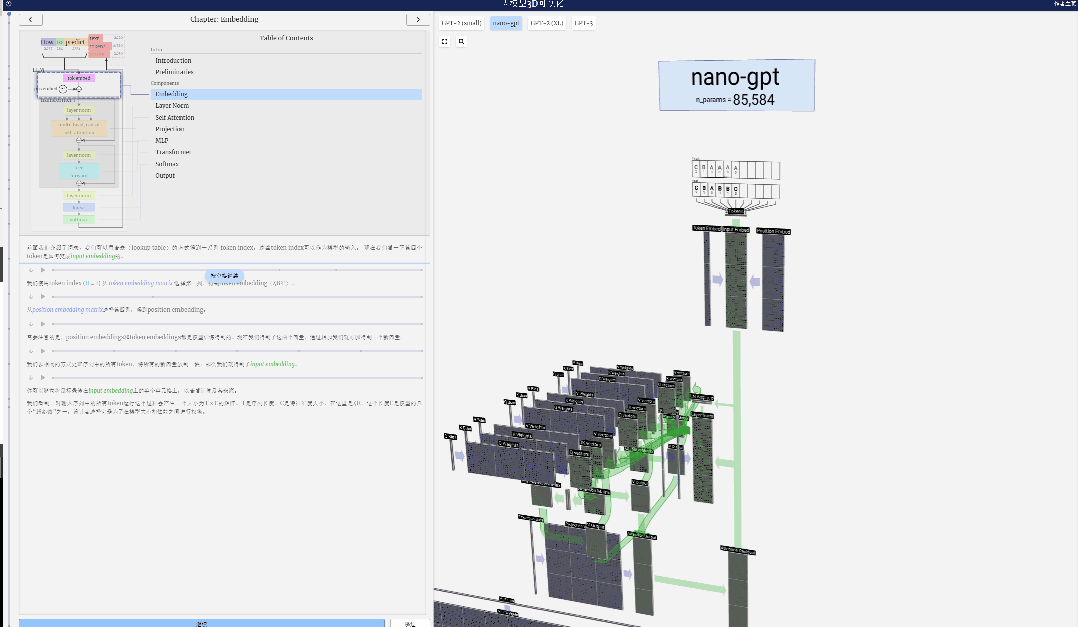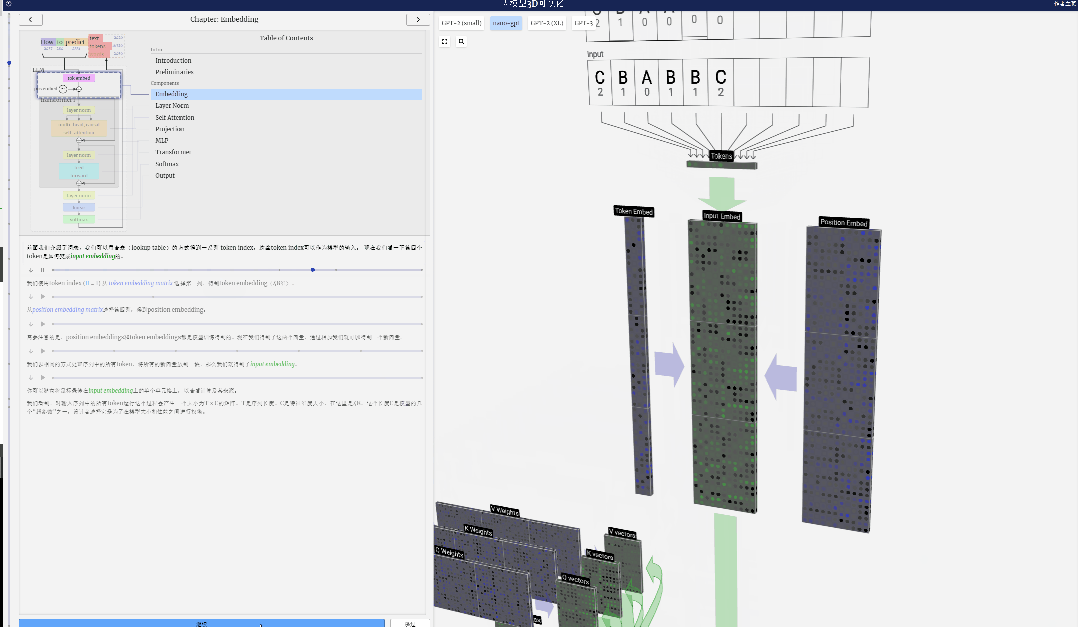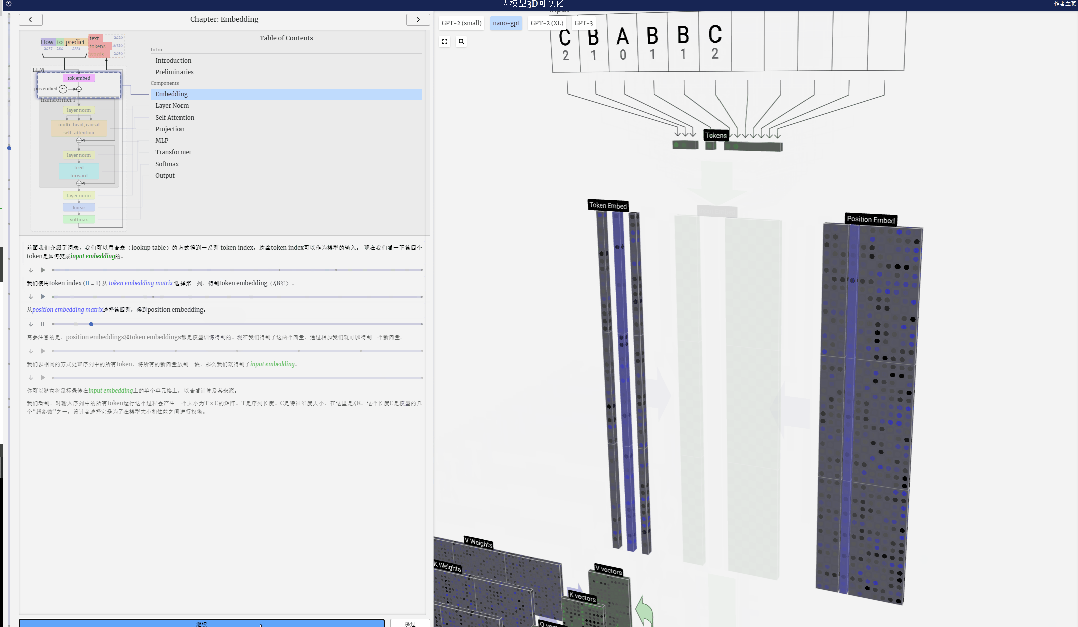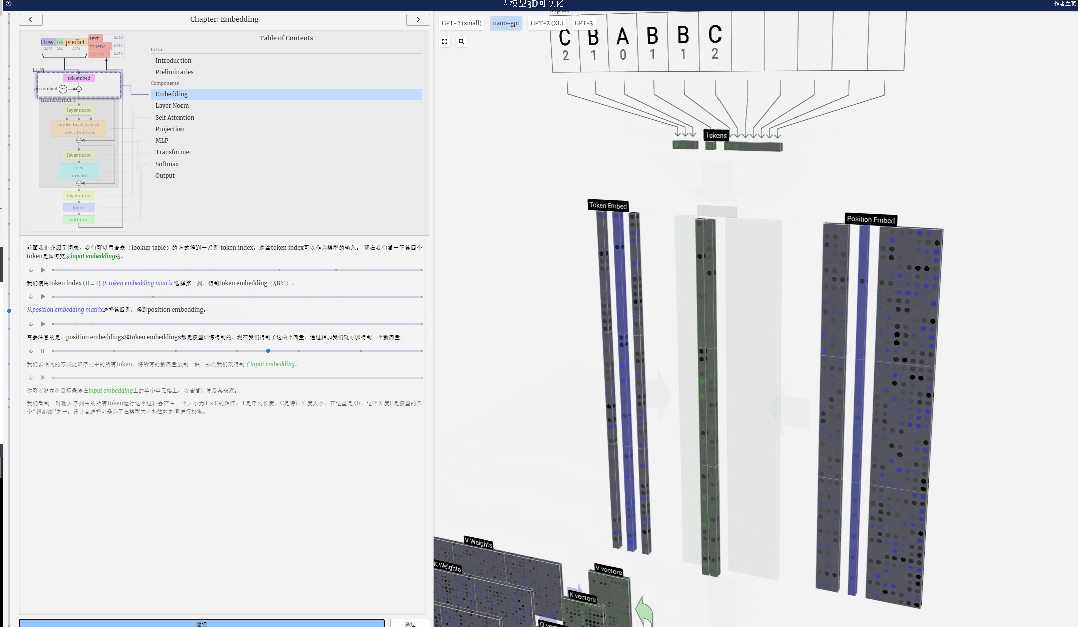
這里,以第4個token(index 3)為例,看看其是如何被用于生成輸入嵌入的第4列向量的。

首先使用token index (這里以B=1為例) 從Token Embedding matrix選擇第二列,得到一個大小為C=48(48維)的列向量,稱為token嵌入(token embedding)。

再從position embedding matrix選擇第四列(「因為這里主要查看第4個位置的(t = 3)token B」),同樣地,得到一個大小為C=48(48維)的列向量,稱為位置嵌入(position embedding)。

需要注意的是,position embeddings和token embeddings都是模型訓練得到的(由藍色表示)。現在我們得到了這兩個向量,通過相加我們就可以得到一個新的大小為C=48的列向量。

接下來,以相同的過程處理序列中的所有token,創建一組包含token值及其位置的向量。

由上圖可以看出,對輸入序列中的所有token運行此過程,會產生一個大小為TxC的矩陣。其中,T表示序列長度。C表示通道(channel),但也稱為特征或維度或嵌入大小,在這里是48。這個長度C是模型的幾個“超參數”之一,設計者選擇它是為了在模型大小和性能之間進行權衡。
這個維度為TxC的矩陣,即為輸入嵌入(input embedding),并通過模型向下傳遞。
小Tip: 隨意將鼠標懸停在input embedding上的單個單元格上,可以查看計算及其來源。
層歸一化Layer Norm
前面得到的input embedding矩陣即是Transformer層的輸入。
Transformer層的第一步是對input embedding矩陣進行層歸一化處理(layer normalization),這是對輸入矩陣每一列的值分別進行歸一化的操作。
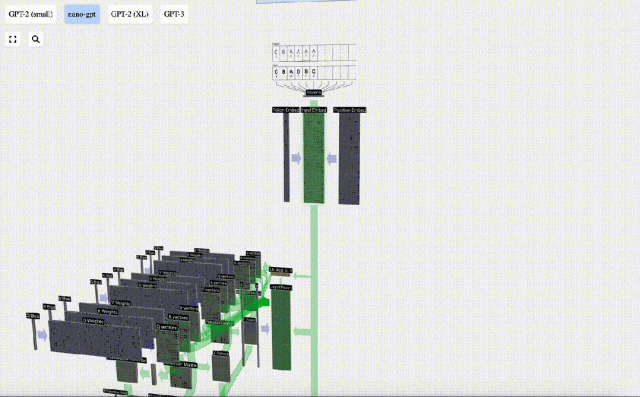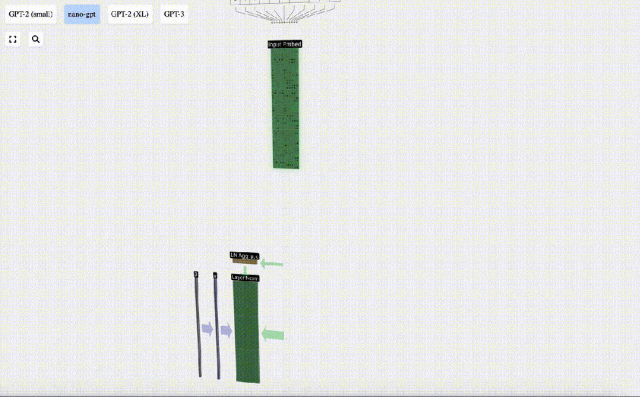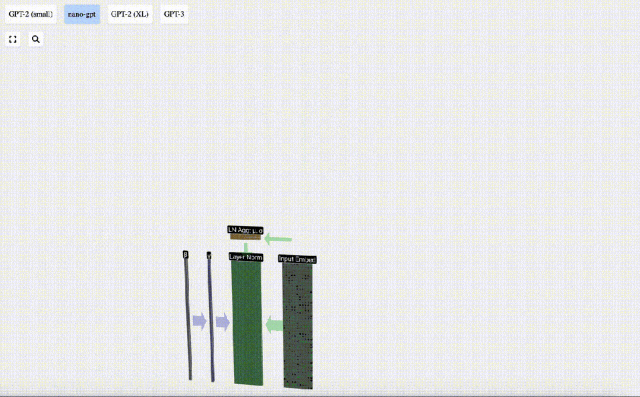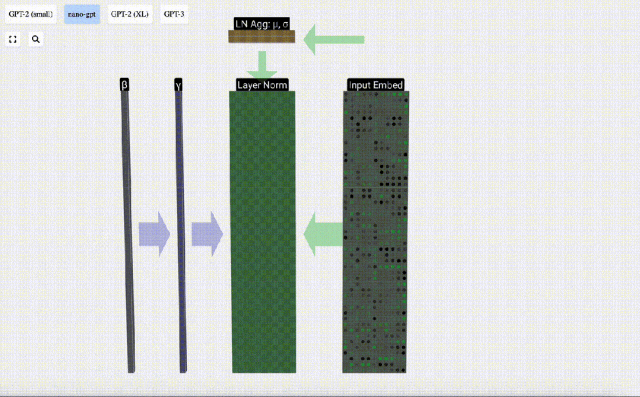
歸一化是深度神經網絡訓練中的一個重要步驟,它有助于提高模型在訓練過程中的穩定性。
我們可以將矩陣的列單獨分開來看,下面以第四列為例。
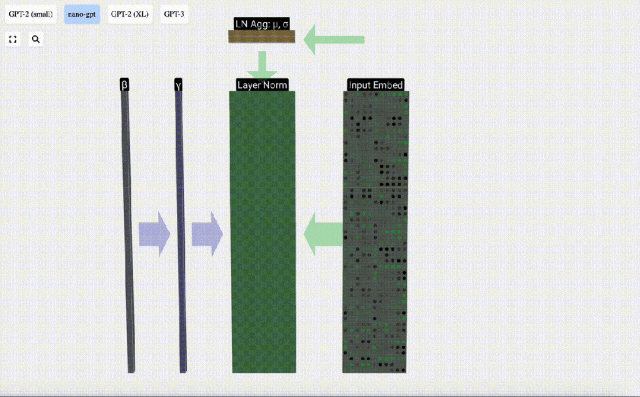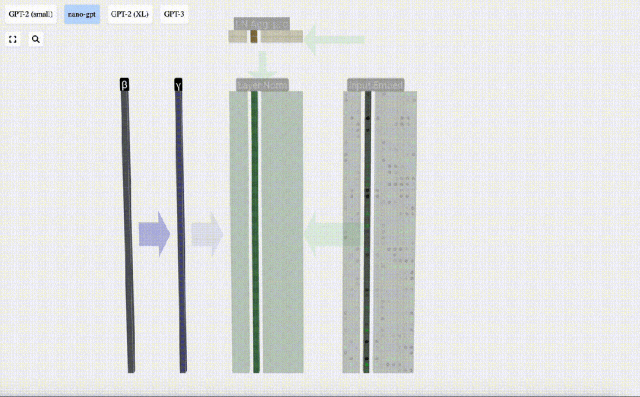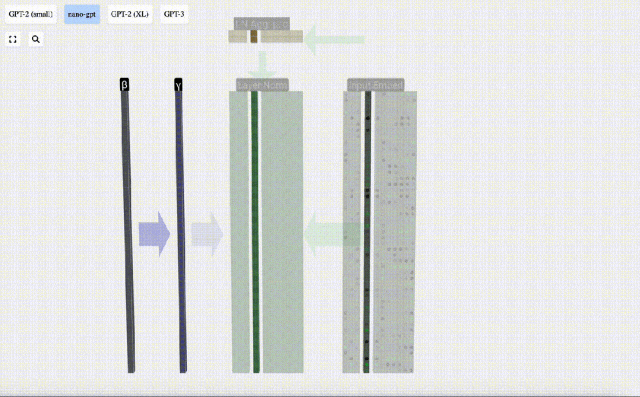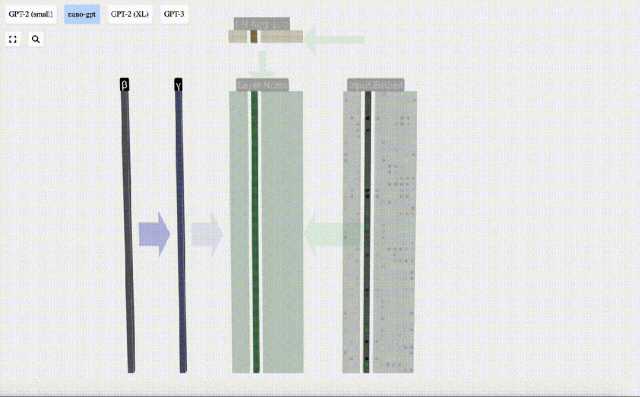
歸一化的目標是使得每列的數值均值為0,標準差為1。為實現這一目標,需要計算每一列的均值和標準差,然后讓每一列減去相應均值和除以相應標準差。
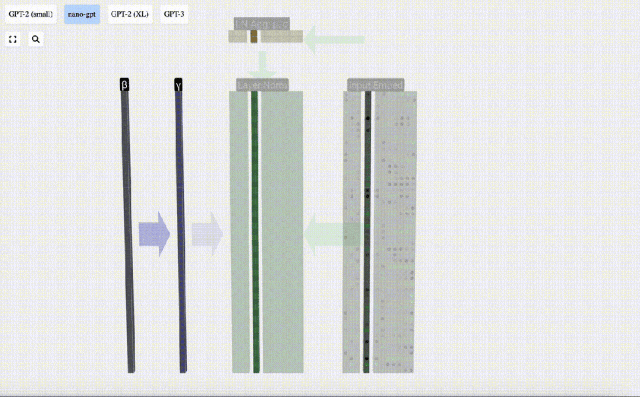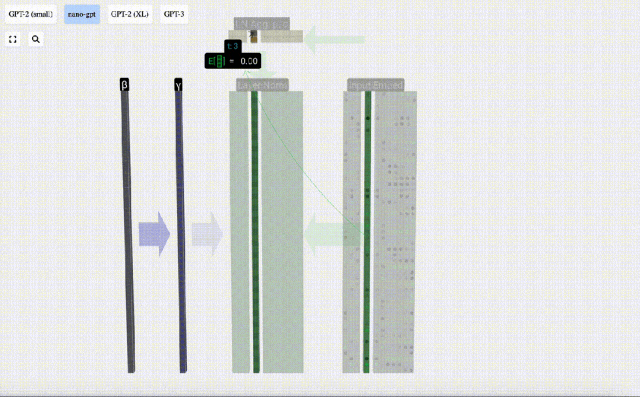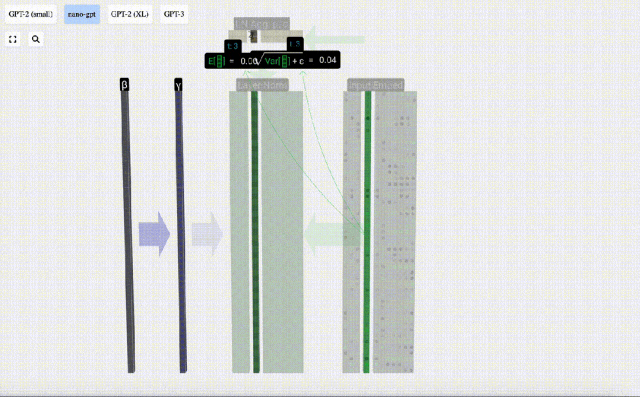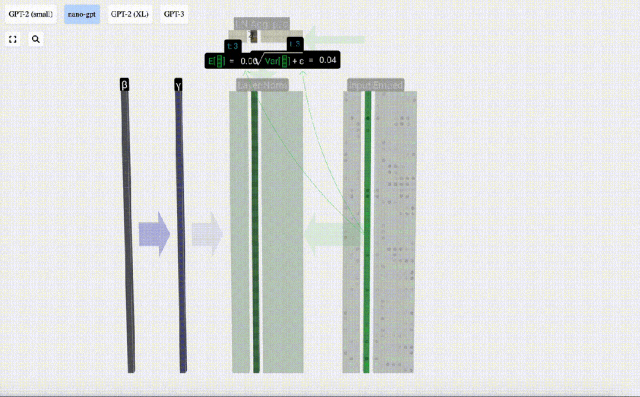
這里使用E[x]來表示均值, Var[x]來表示方差(標準差的平方)。epsilon(ε = 1×10^-5)是防止出現除0錯誤。
計算并存儲歸一化后的結果,然后乘以學習權重weight(γ)并加上偏置bias(β),進而得到最終的歸一化結果。
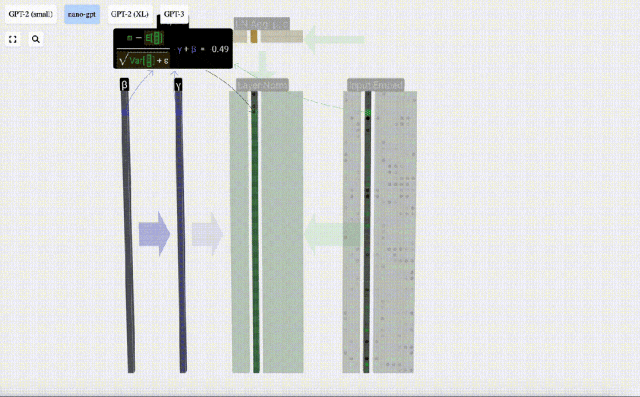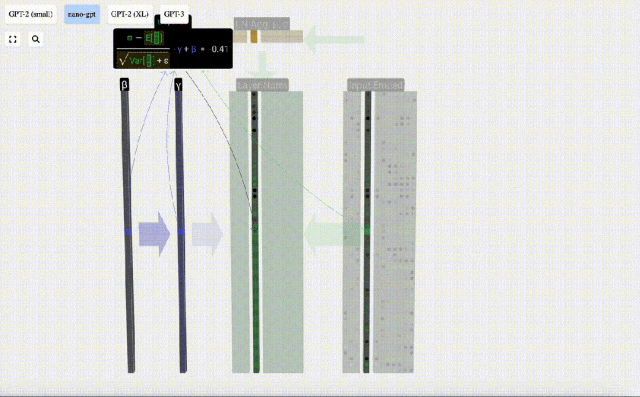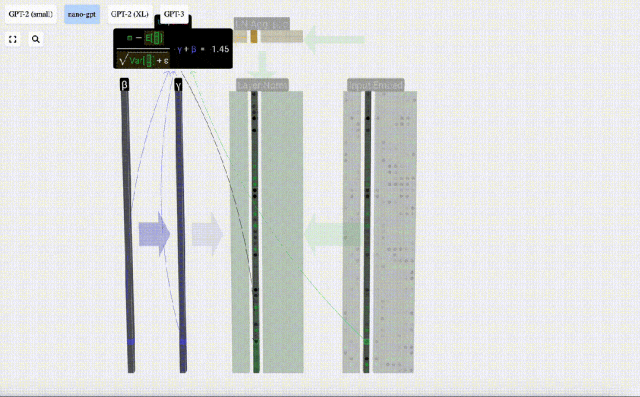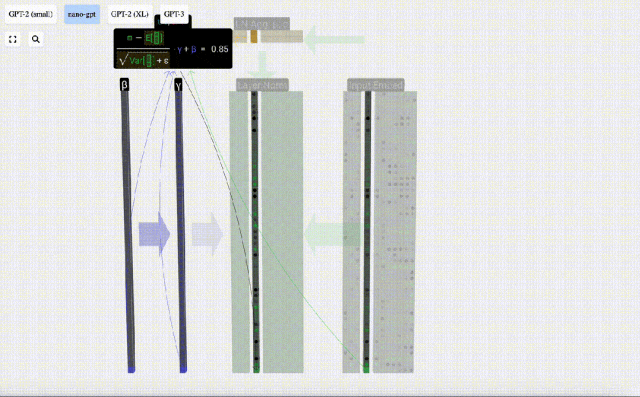
最后,在輸入嵌入矩陣(input embedding matrix)的每一列上執行歸一化操作,就得到了歸一化后的輸入嵌入(normalized input embedding),并將其傳遞給自注意力層(self-attention)。
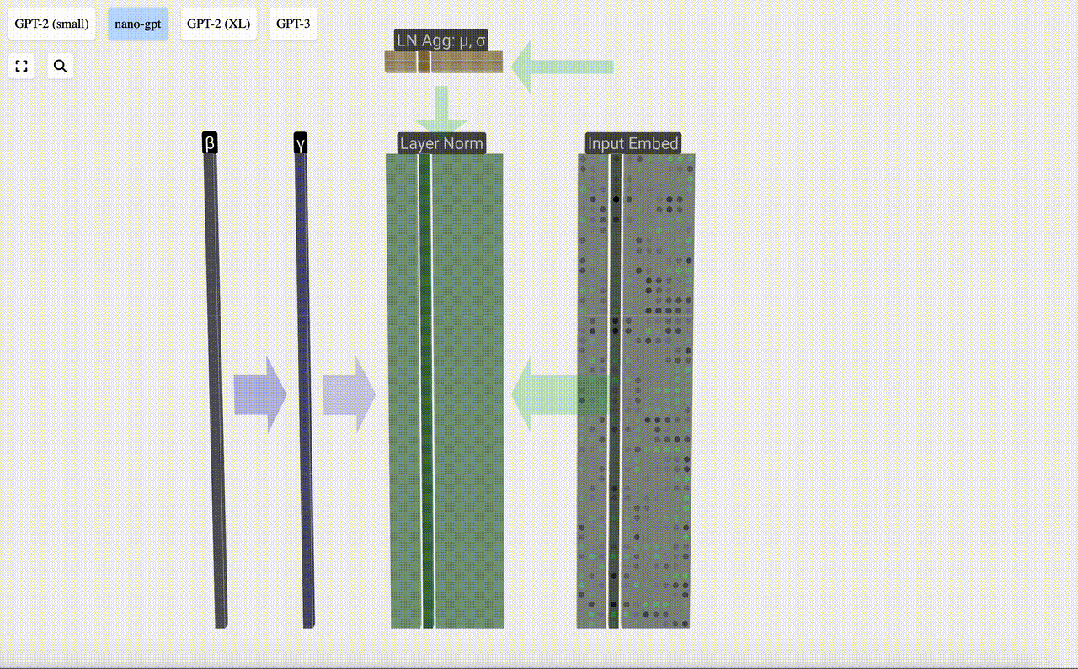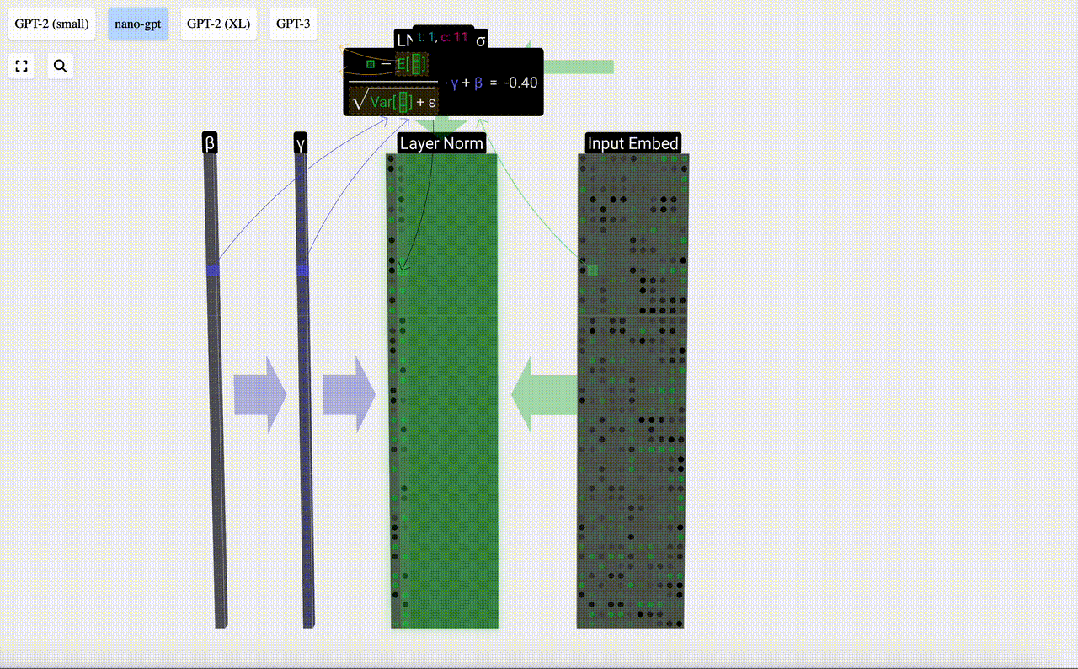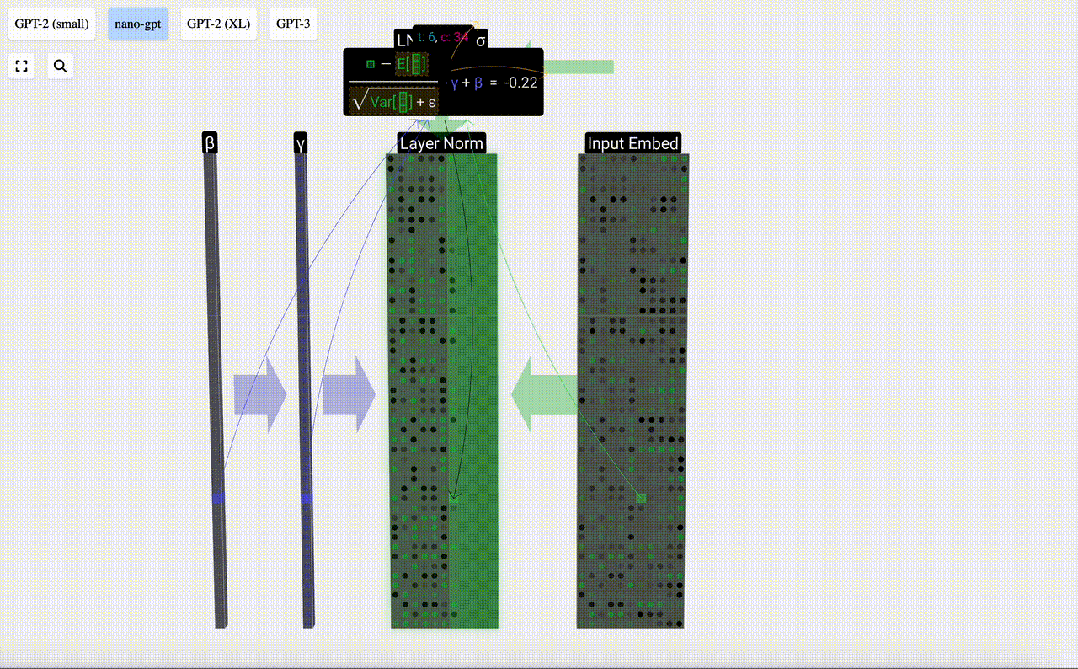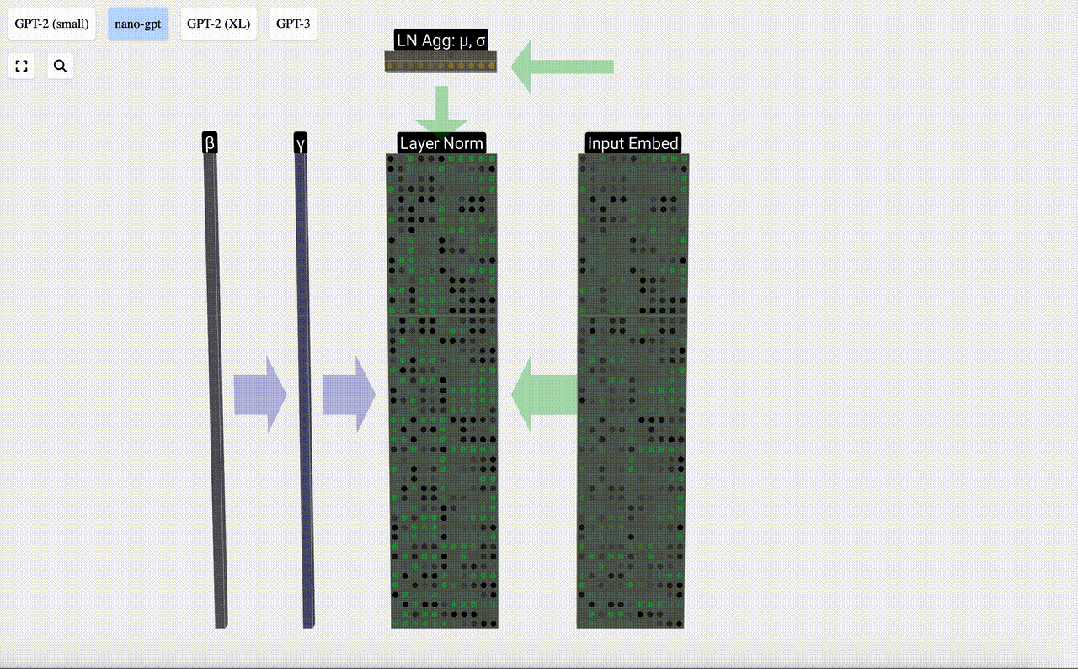
自注意力Self Attention
Self Attention層大概算是Transformer中最核心的部分了,在這個階段,input embedding中的列可以相互“交流”,而其它階段,各列都是獨立存在的。
Self Attention層由多個個自注意力頭組成,本例中有三個自注意力頭。每個頭的輸入是input embedding的1/3部分,我們現在只關注其中一個。

第一步是從normalized input embedding matrix的C列中為每一列生成3個向量,分別是QKV:
- Q: 查詢向量Query vector
- K: 鍵向量Key vector
- V: 值向量Value vector
要生成這些向量,需要采用矩陣-向量乘法,外加偏置。每個輸出單元都是輸入向量的線性組合。
例如,對于查詢向量,即是由Q權重矩陣的一行和輸入矩陣的一列之間的點積運算完成的。
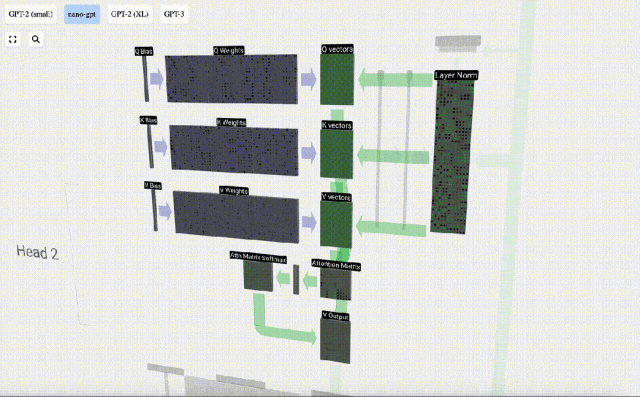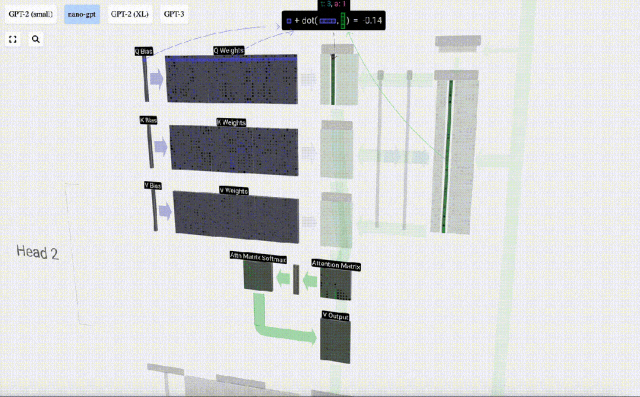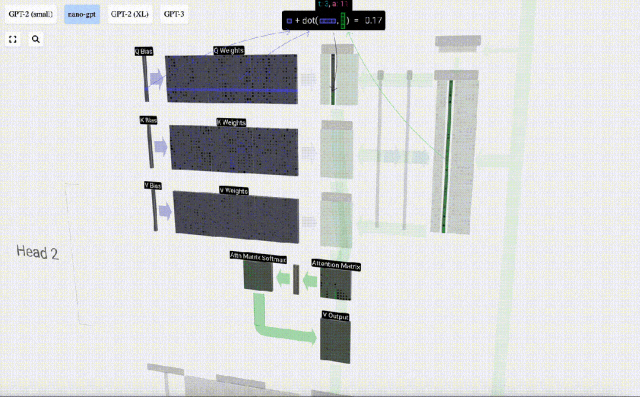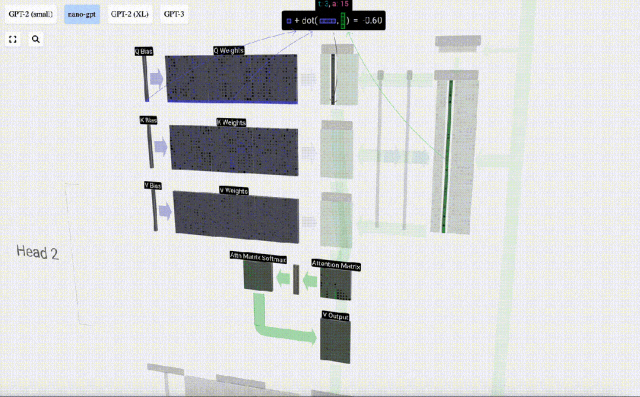
點積的操作很簡單,就是對應元素相乘然后相加。
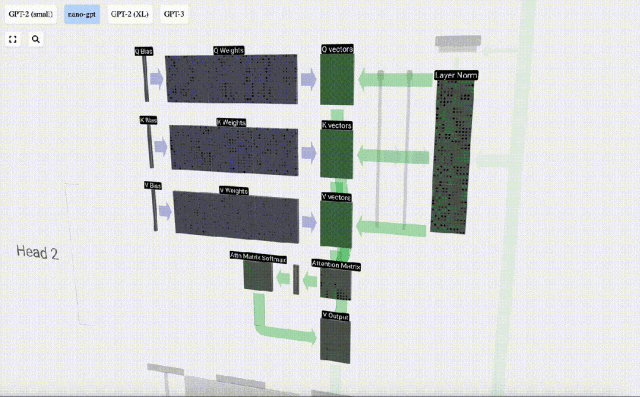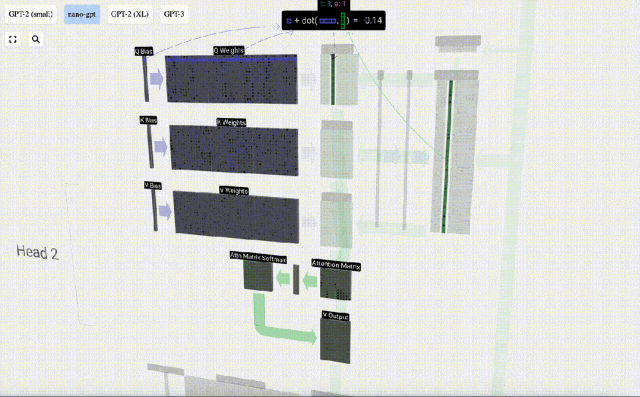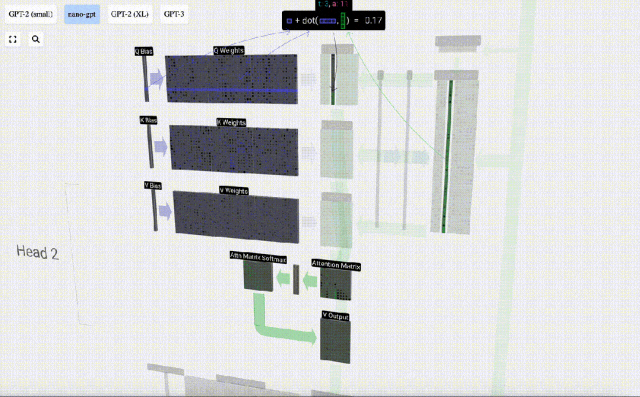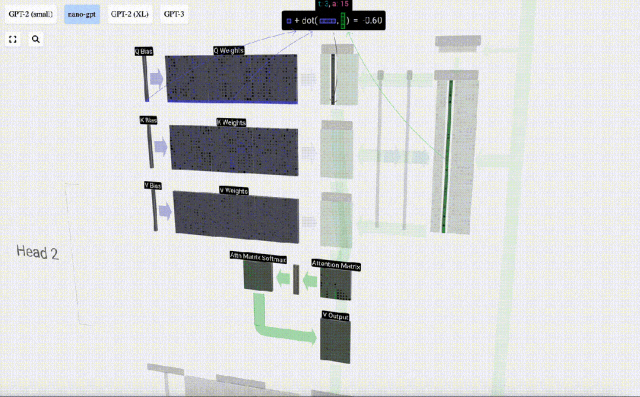
這是一種確保每個輸出元素都能受到輸入向量中所有元素影響的通用而簡單的方法(這種影響由權重決定)。因此,它經常出現在神經網絡中。
在神經網絡中,這種機制經常出現是因為它允許模型在處理數據時考慮到輸入序列的每個部分。這種全面的注意力機制是許多現代神經網絡架構的核心,特別是在處理序列數據(如文本或時間序列)時。
我們對Q, K, V向量中的每個輸出單元重復此操作:
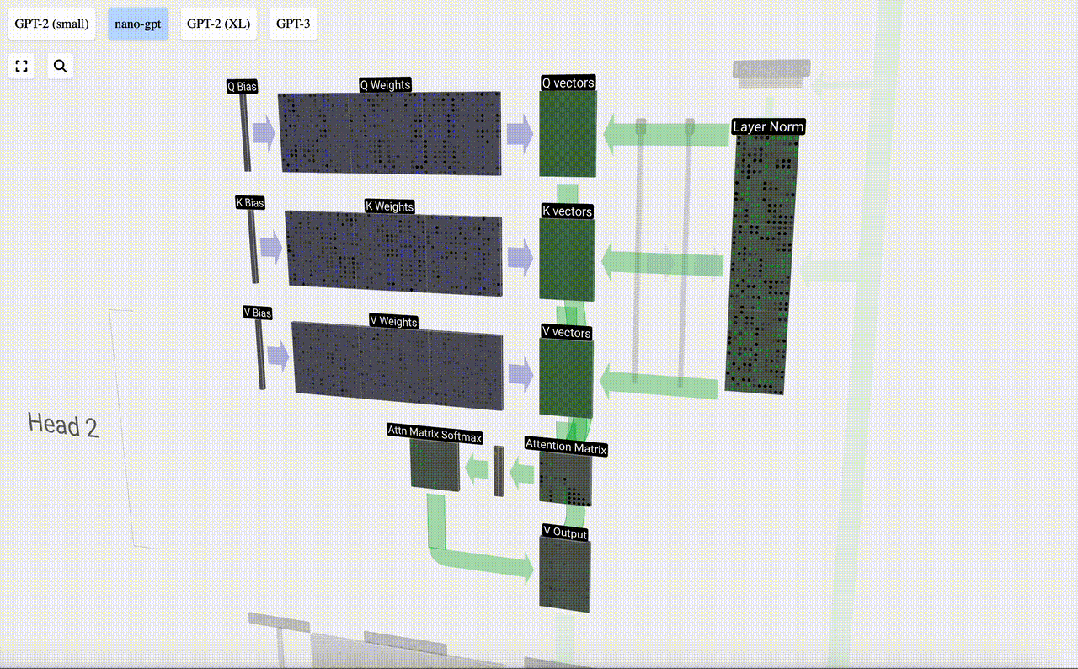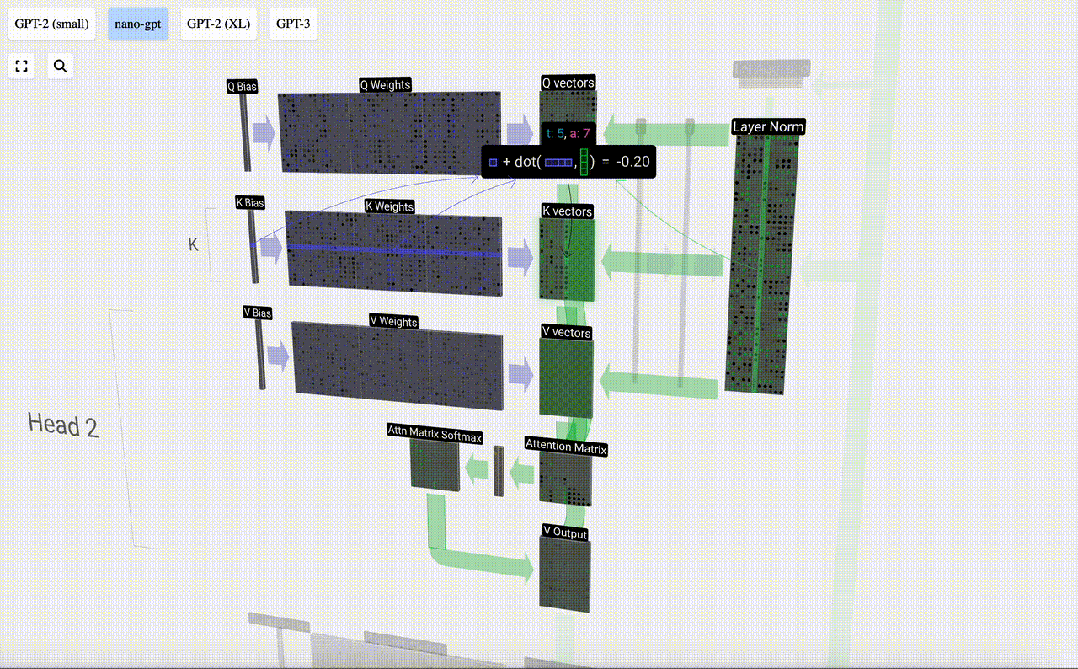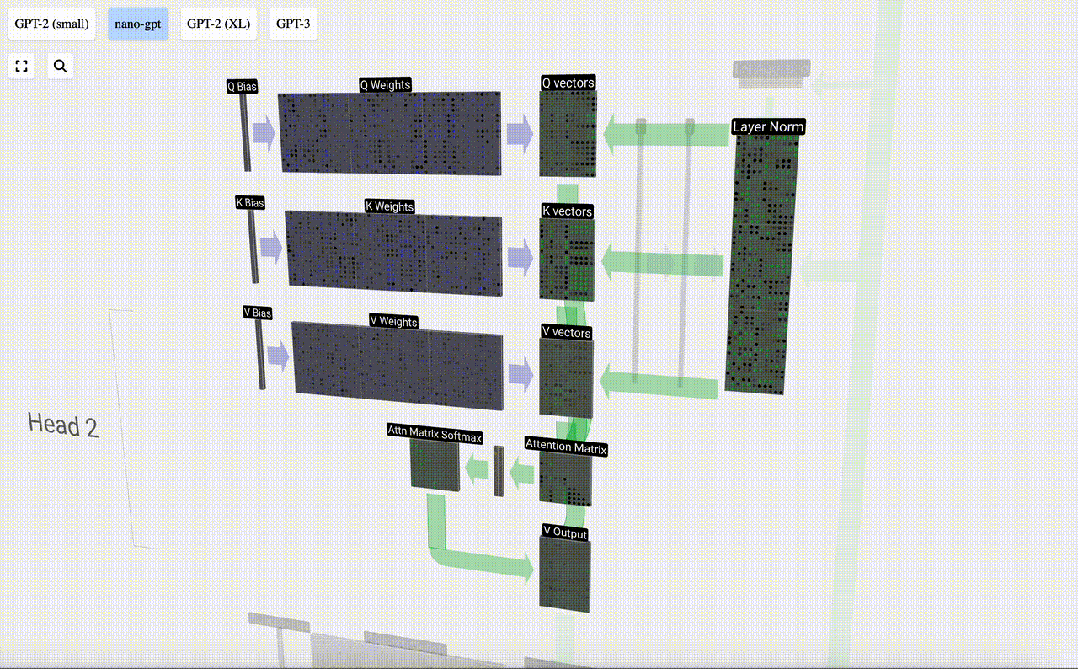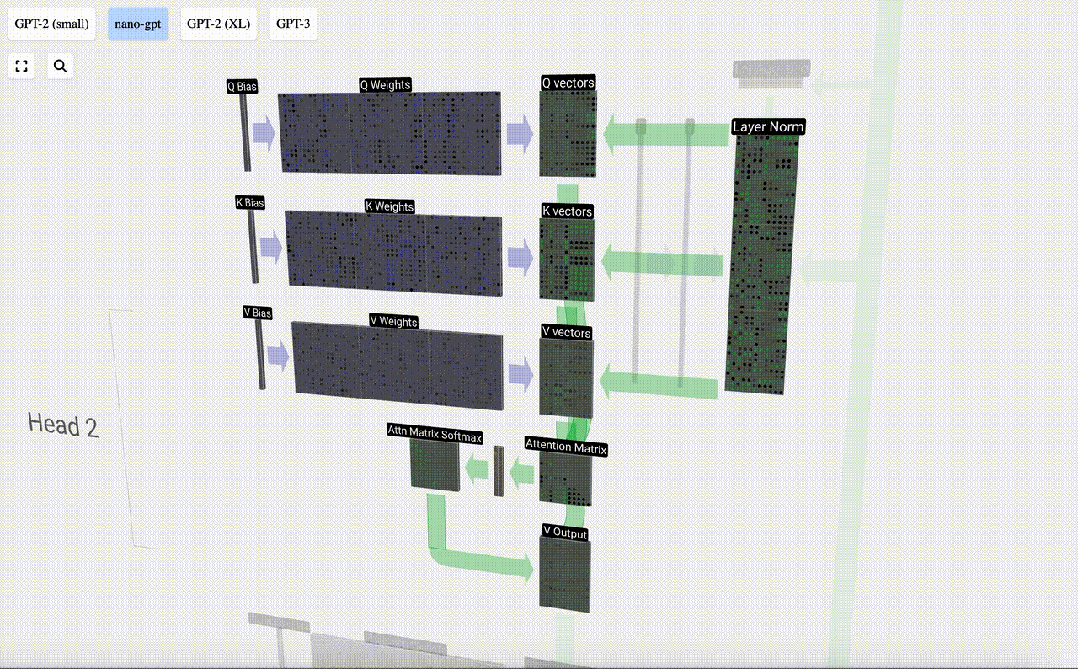
我們如何使用我們的 Q(查詢)、K(鍵)和 V(值)向量呢?它們的命名給了我們一個提示:‘鍵’和‘值’讓人想起字典類型,鍵映射到值。然后‘查詢’是我們用來查找值的手段。

在Self Attention的情況下,我們不是返回單個向量(詞條),而是返回向量(詞條)的某種加權組合。為了找到這個權重,我們計算一個Q向量與每個K向量之間的點積,再加權歸一化,最后用它與相應的V向量相乘,再將它們相加。

以第6列為例(t=5),將從這一列開始查詢:
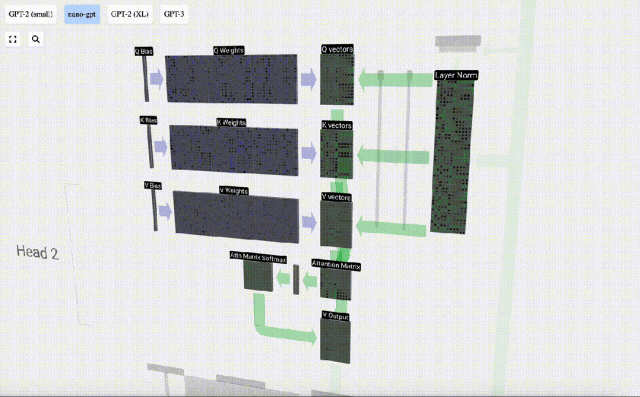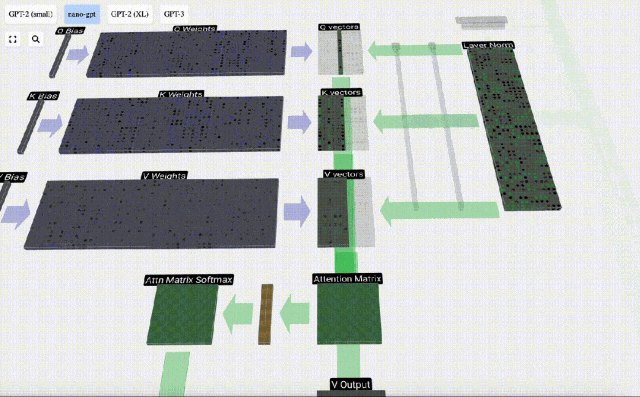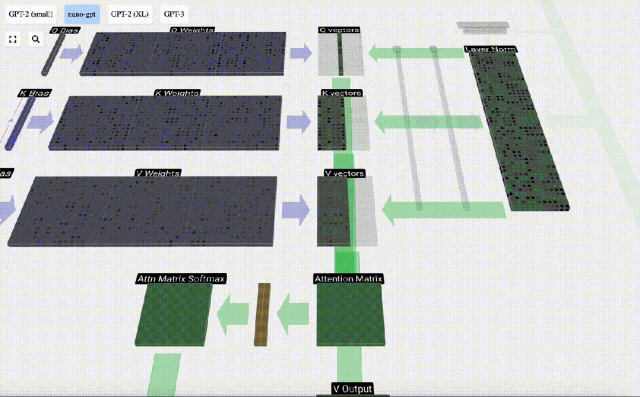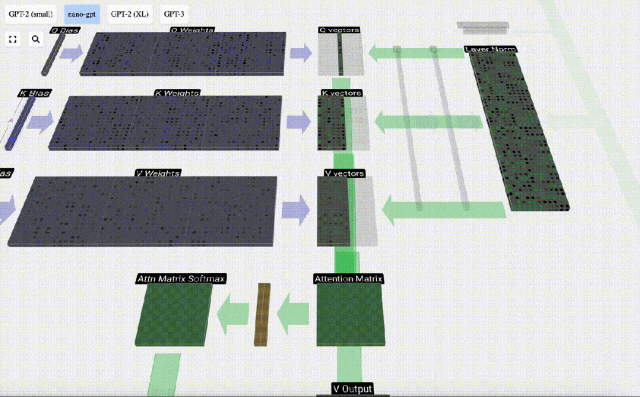
由于attention matrix的存在,KV的前6列是可以被查詢到的,Q值是當前時間。
首先計算當前列(t=5)的Q向量與之前各列(前6列)的K向量之間的點積。然后將其存儲在注意力矩陣的相應行(t=5)中。
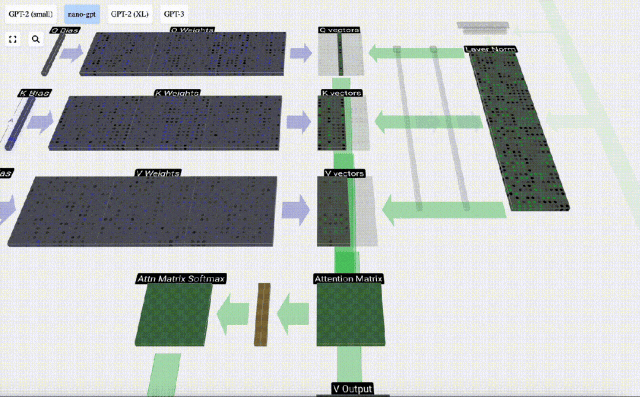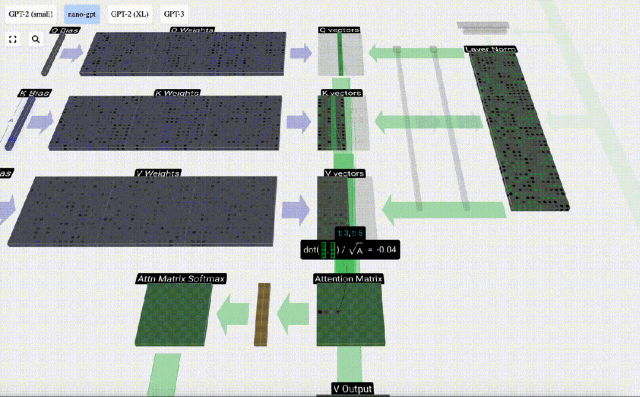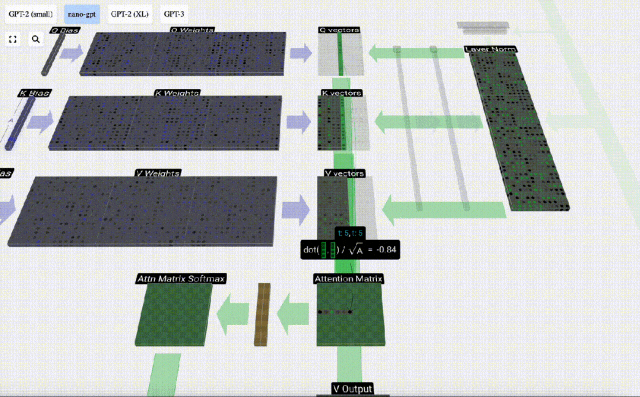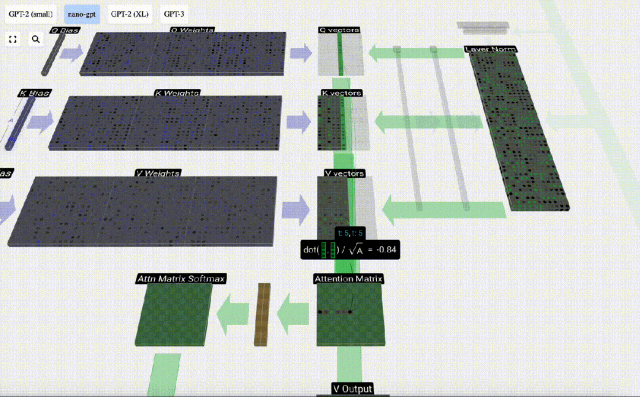
點積的大小衡量了兩個向量間的相似度,點積越大越相似。
而只將Q向量與過去的K向量進行運算,使得它成為因果自注意力。也就是說,token無法‘看到未來的信息’。
因此,在求出點積之后,要除以sqrt(A),其中A是QKV向量的長度,進行這種縮放是為了防止大值在下一步的歸一化(softmax)中占主導地位。
接下來,又經過了softmax操作,將值域范圍縮小到了0到1。
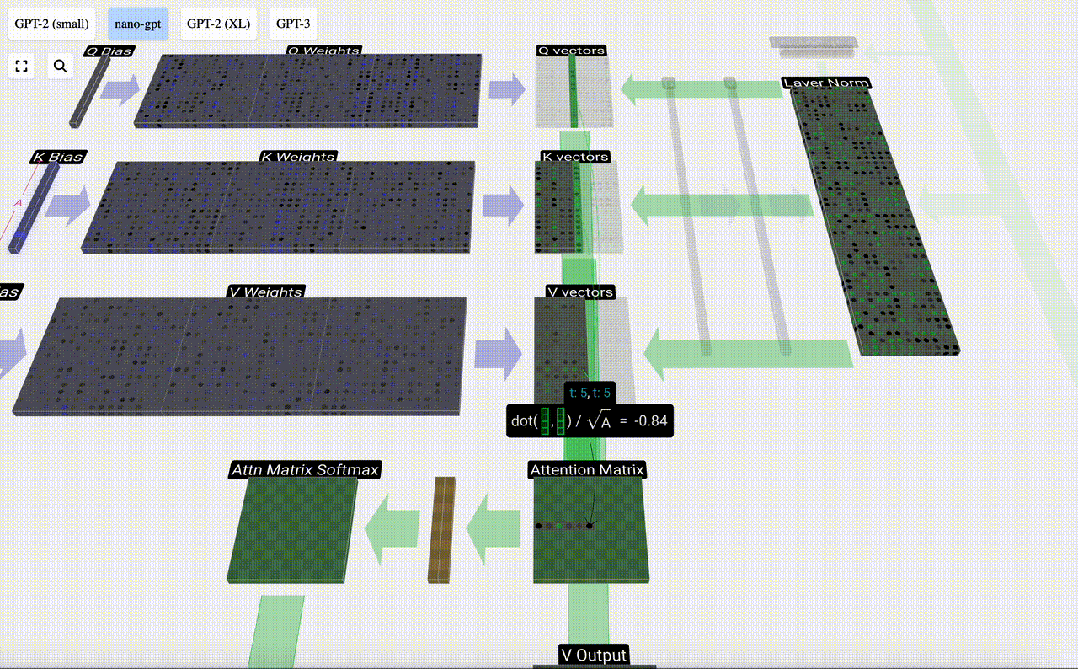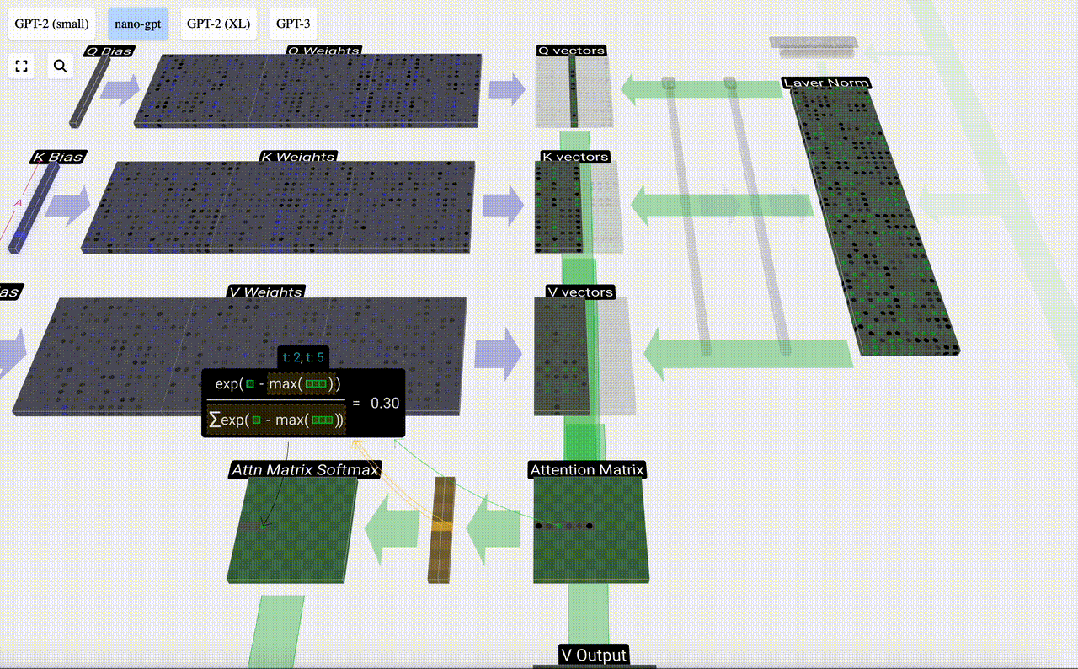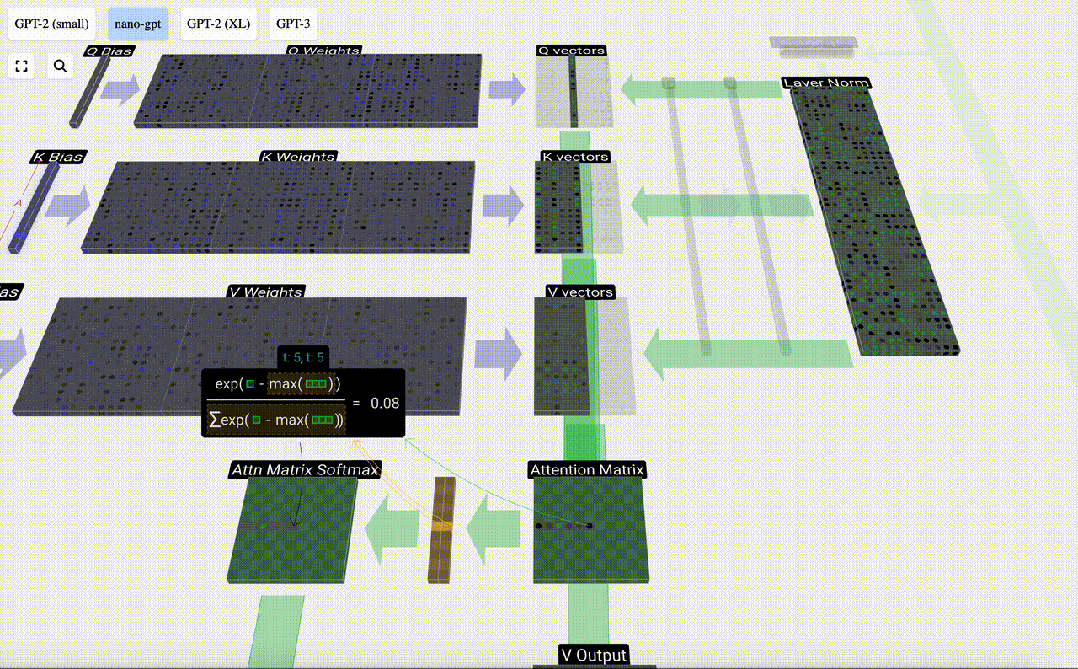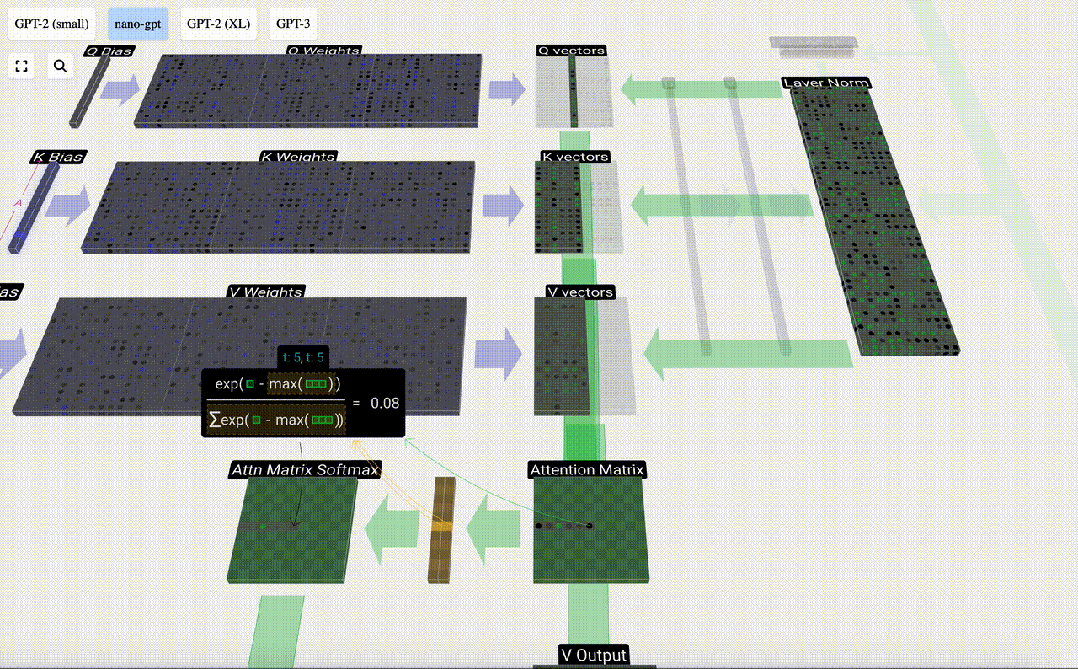
最后,就可以得出這一列(t=5)的輸出向量。查看歸一化attention matrix的(t=5)行,并將每個元素與其他列的相應V向量相乘。
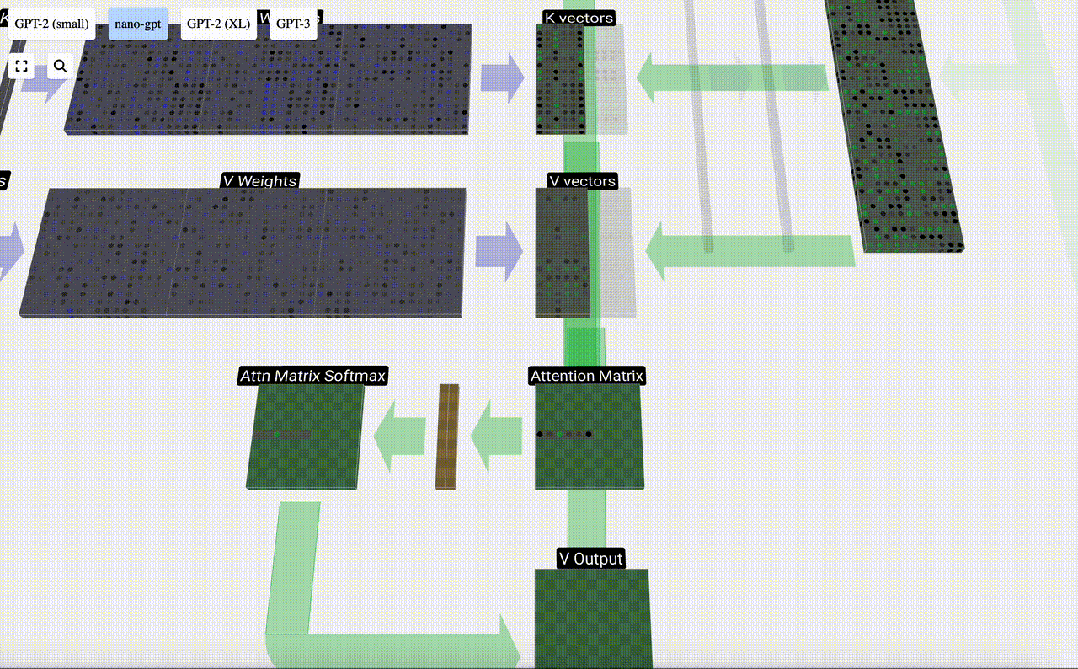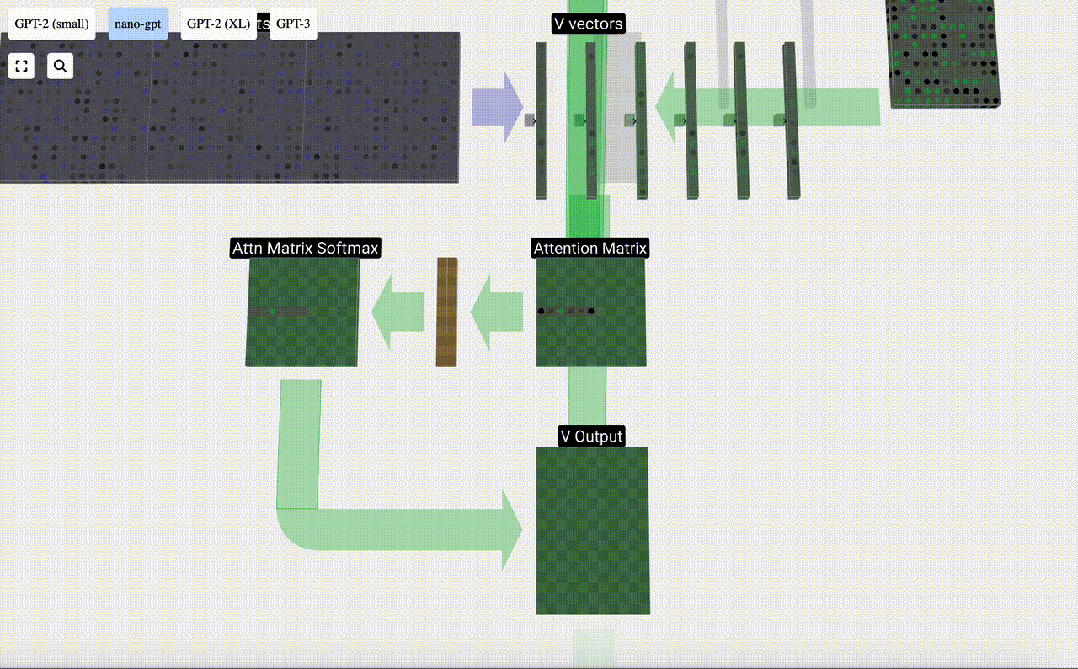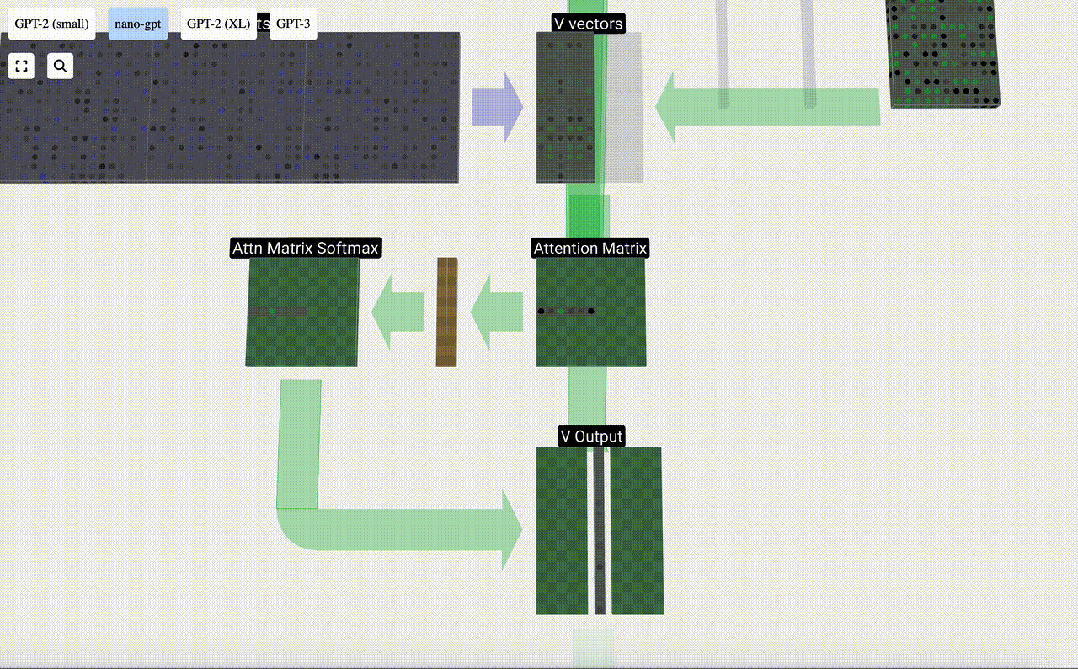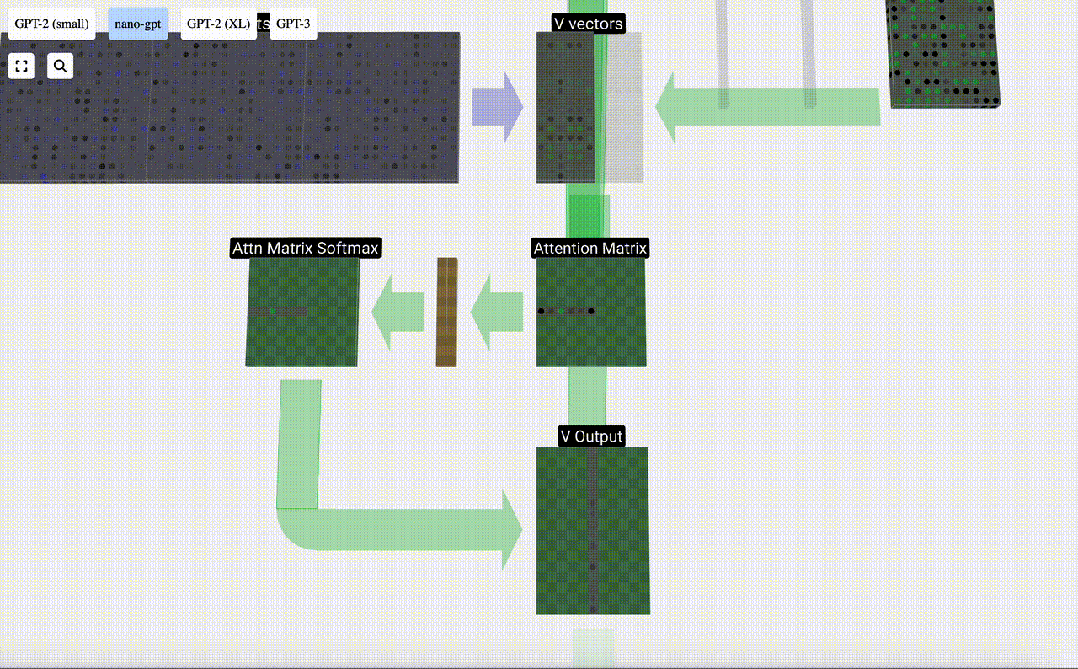
然后,我們可以將這些向量相加,得出輸出向量。因此,輸出向量將以高分列的V向量為主。
現在我們應用到所有列上。
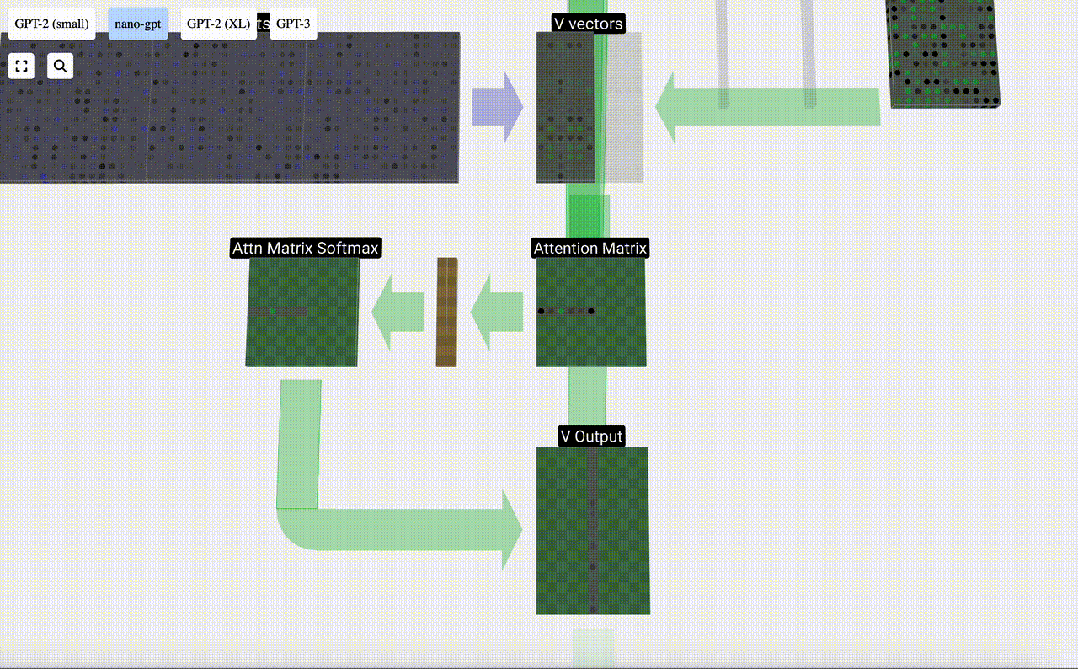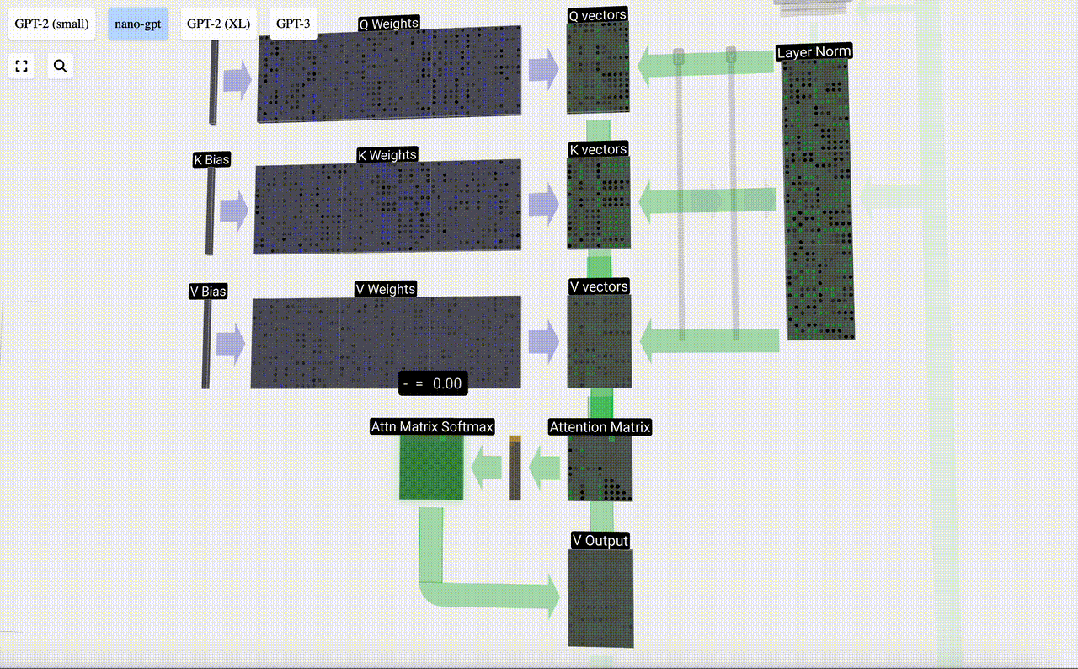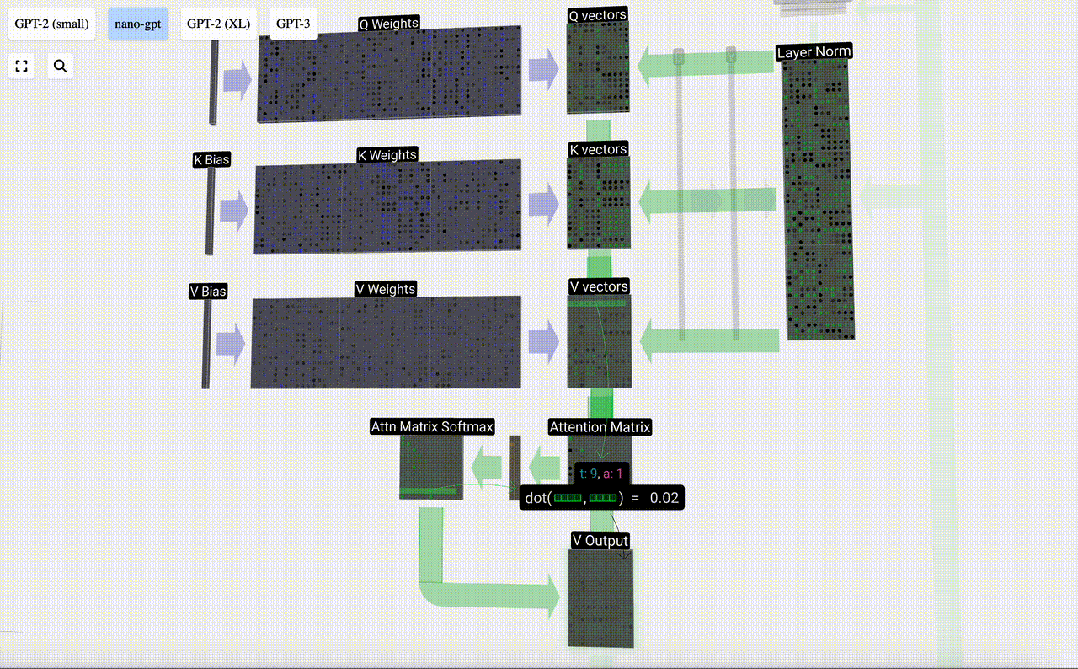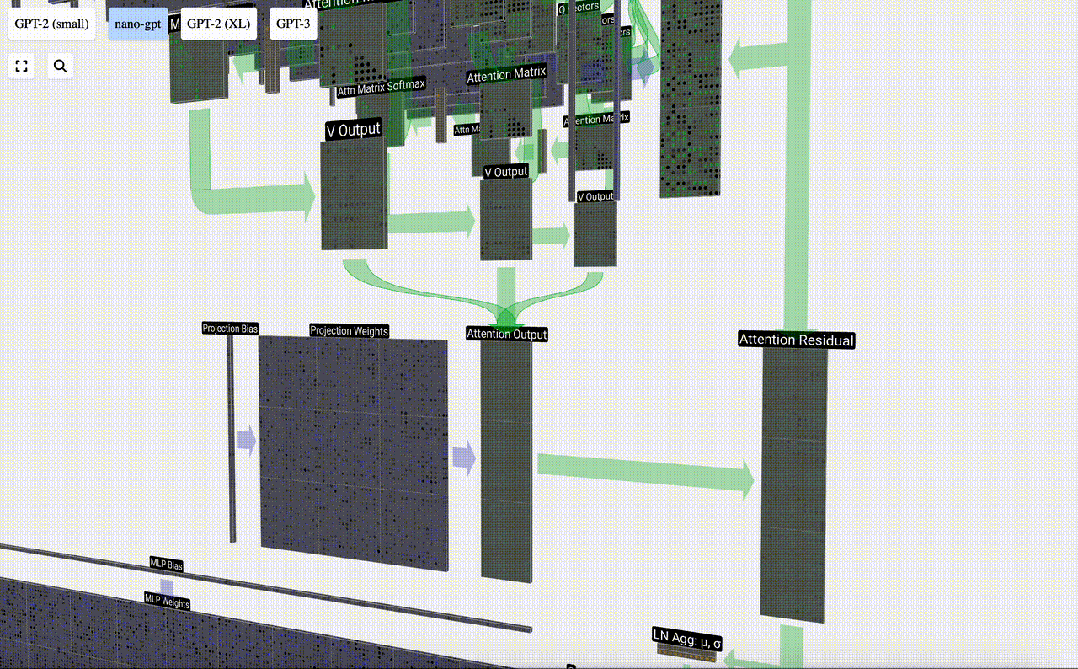
這就是Self Attention層中一個頭的處理過程。「因此,Self Attention的主要目標是每一列都想從其他列中找到相關信息并提取其值,它通過將其 Query 向量與那些其他列的 Key 進行比較來實現這一點。增加的限制是它只能向過去看。」
投影Projection
在Self Attention操作之后,我們會從每個頭得到一個輸出。這些輸出是受Q和K向量影響而適當混合的V向量。要合并每個頭的輸出向量,我們只需將它們堆疊在一起即可。因此,在t=4時,我們將從3個長度為A=16的向量疊加形成1個長度為C=48的向量。
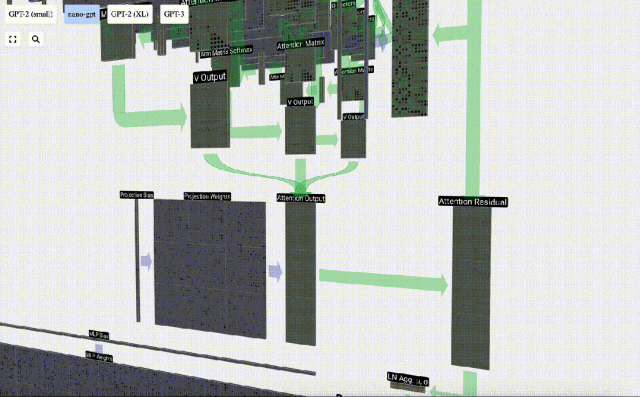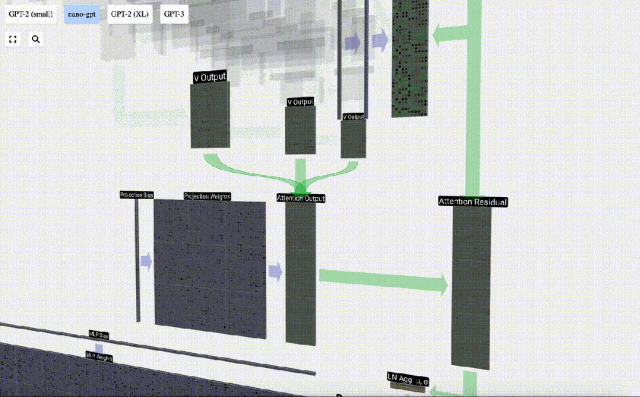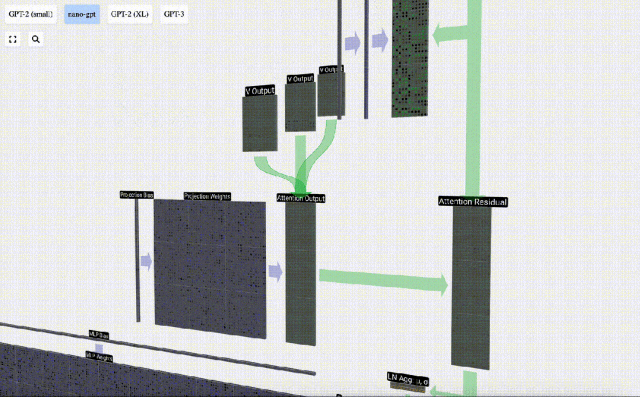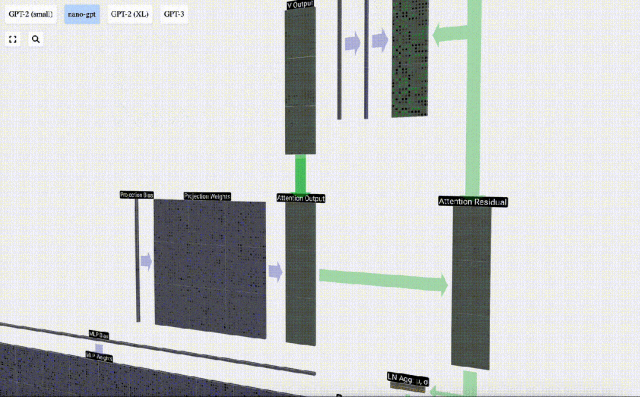
值得注意的是,在GPT中,頭(A=16)內向量的長度等于 C/num_heads。這確保了當我們將它們重新堆疊在一起時,能得到原來的長度C。
在此基礎上,我們進行投影,得到該層的輸出。這是一個簡單的矩陣-向量乘法,以每列為單位,并加上偏置。
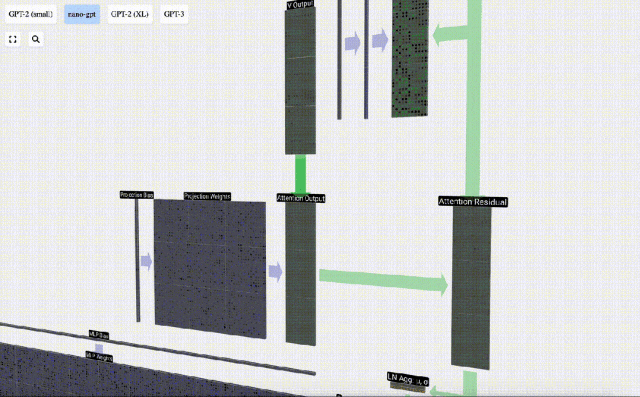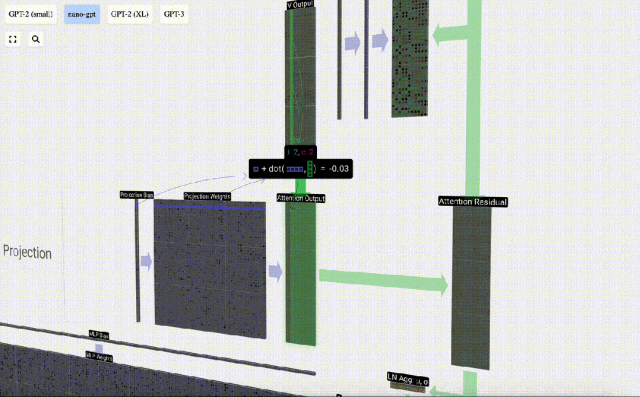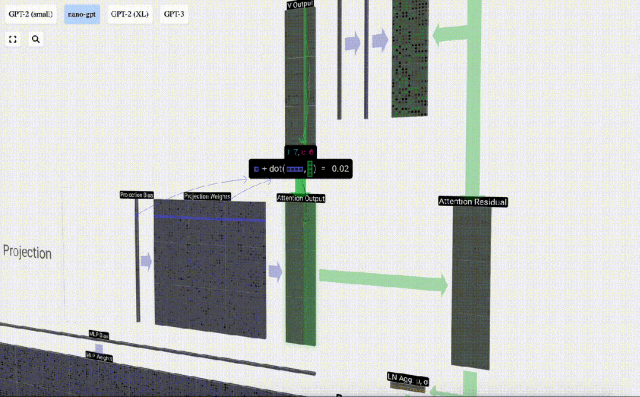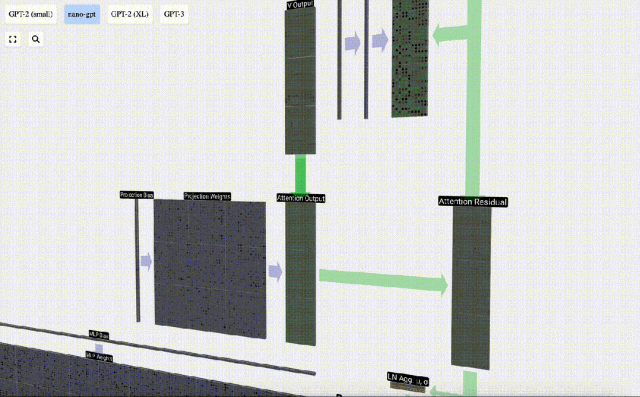
現在我們有了Self Attention的輸出。
我們沒有將這個輸出直接傳遞到下一階段,而是將它以元素的方式添加到input embedding中。 這個過程,用綠色垂直箭頭表示,被稱為殘差連接(residual connection)或殘差路徑(residual pathway)。
與Layer Normalization一樣,殘差網絡對于實現深度神經網絡的有效學習至關重要。
現在有了self-attention的結果,我們可以將其傳遞到Transformer的下一層:前饋網絡。
多層感知機MLP
在Self Attention之后,Transformer模塊的下一部分是MLP(多層感知機),在這里它是一個有兩層的簡單神經網絡。
與Self Attention一樣,在向量進入MLP之前,我們需進行層歸一化處理。
同時,在MLP中,還需對每個長度為C=48的列向量(獨立地)進行以下處理:
- 添加帶偏置的線性變換(也就是矩陣-向量乘法并加上偏置的運算),轉換為長度為 4 * C 的向量。
- GELU 激活函數(逐元素應用)。
- 進行帶偏置的線性變換,再變回長度為 C 的向量。
讓我們追蹤其中一個向量:

MLP具體處理如下:
首先進行矩陣-向量乘法運算并加上偏置,將向量擴展為長度為 4*C 的矩陣。(注意這里的輸出矩陣是經過轉置的,為了形象化)
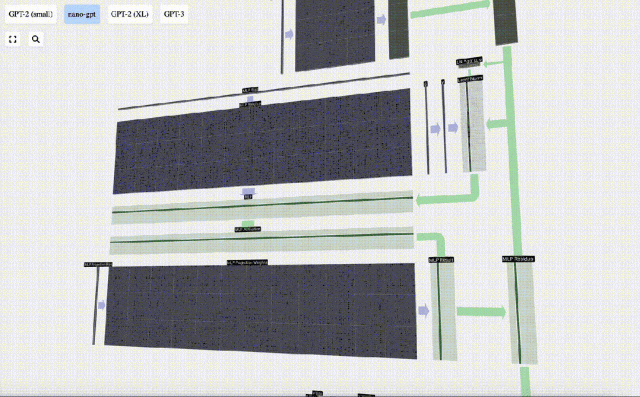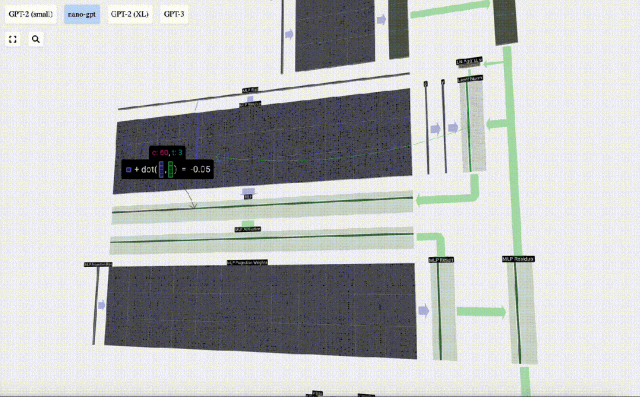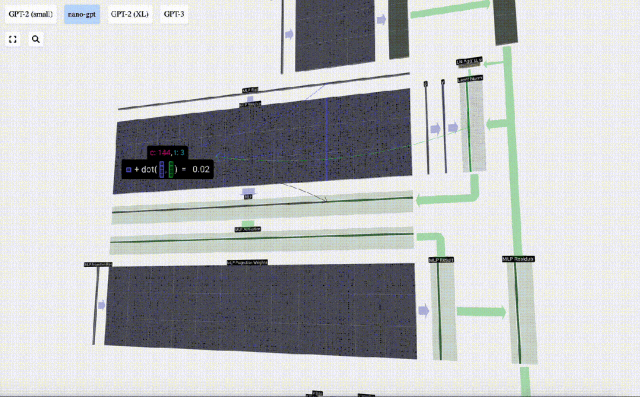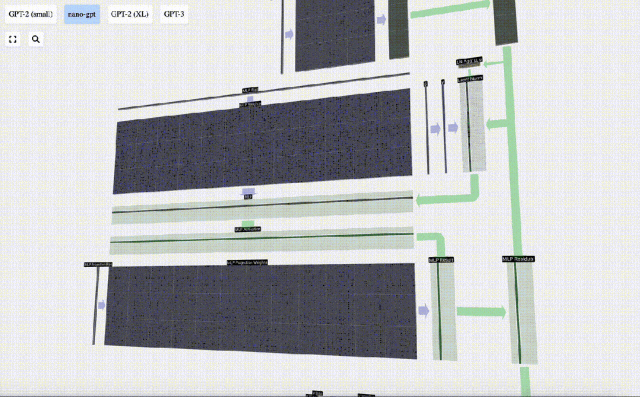
接下來,對向量的每個元素應用GELU激活函數。這是任何神經網絡的關鍵部分,我們需要在模型中引入了一些非線性。所使用的具體函數 GELU,看起來很像 ReLU 函數 max(0, x),但它有一個平滑的曲線,而不是尖銳的角。
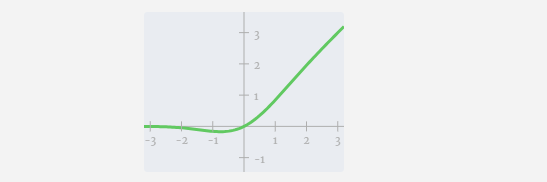
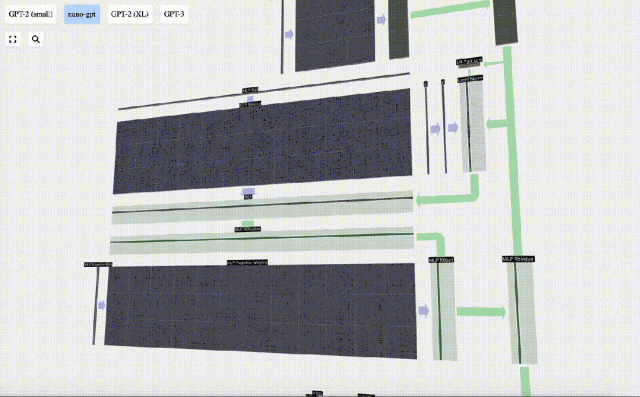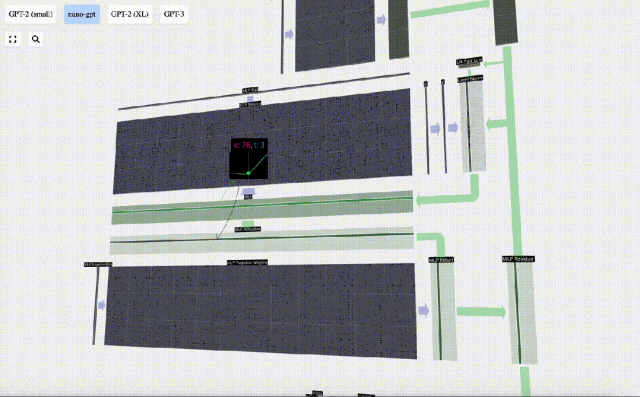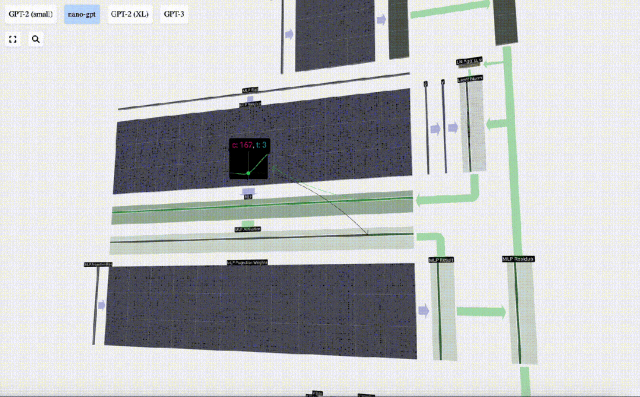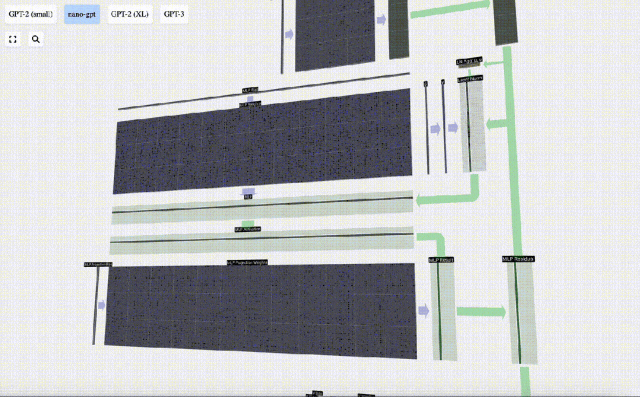
然后,通過另一個帶偏置的矩陣-向量乘法,將向量投影回長度C。
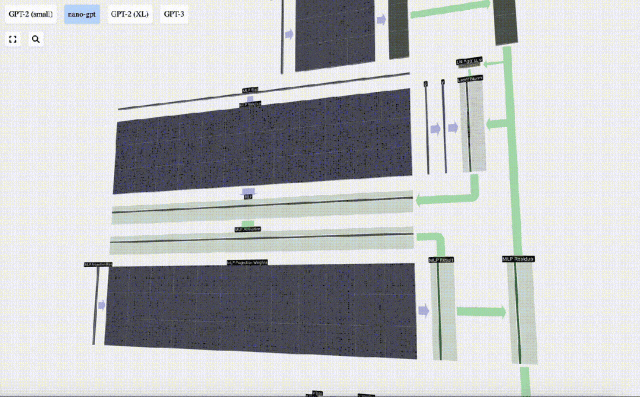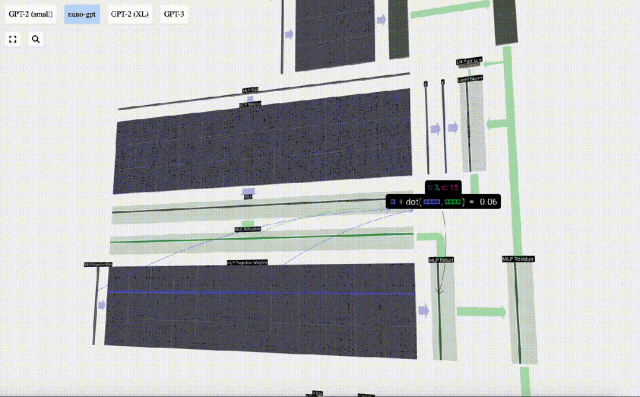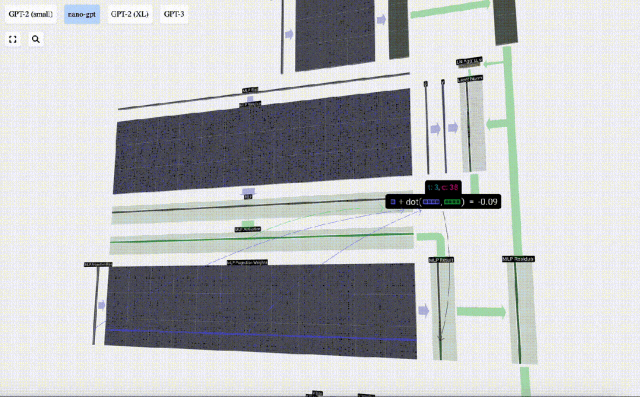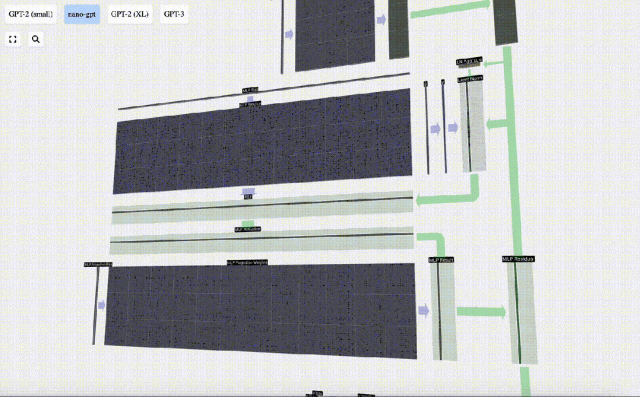
這里也有一個殘差網絡,與自注意力+投影部分一樣,我們將MLP的結果按元素順序添加到input中。
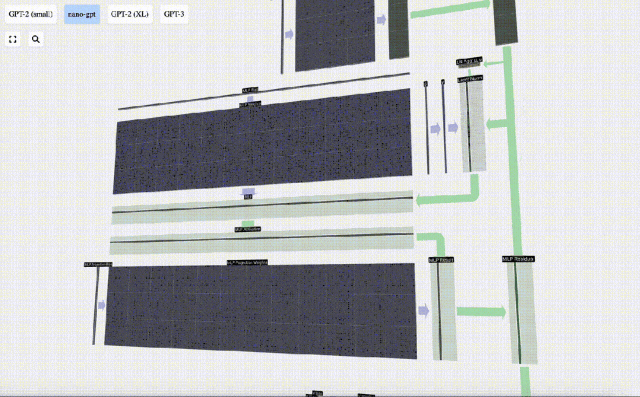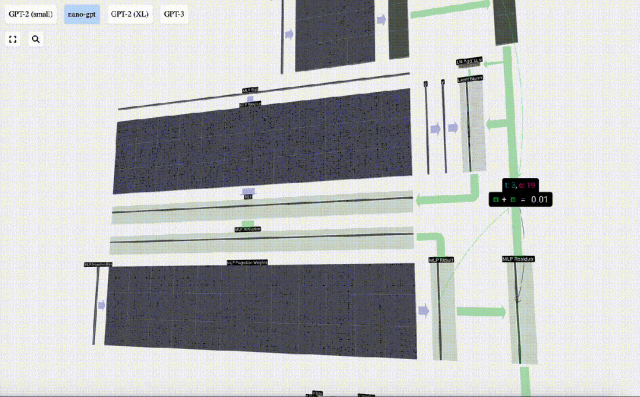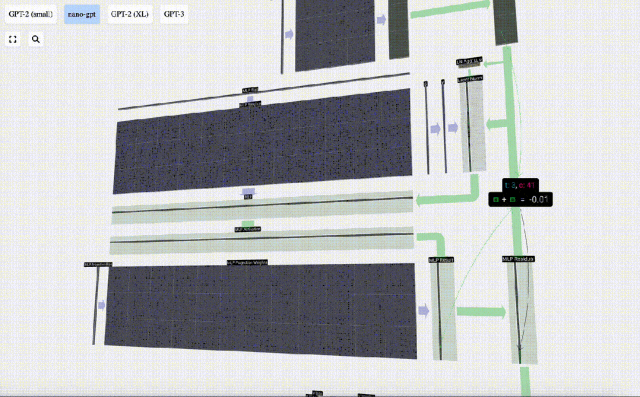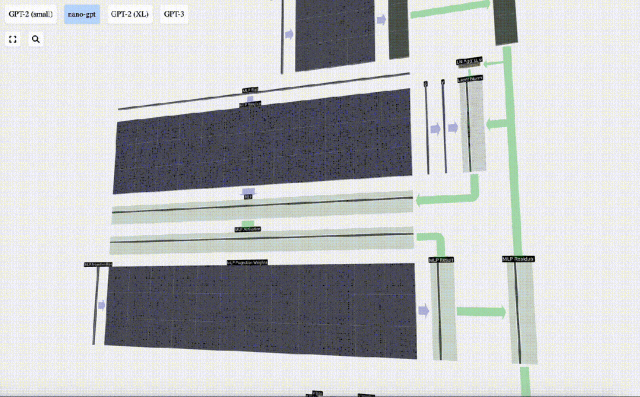
重復這些操作。
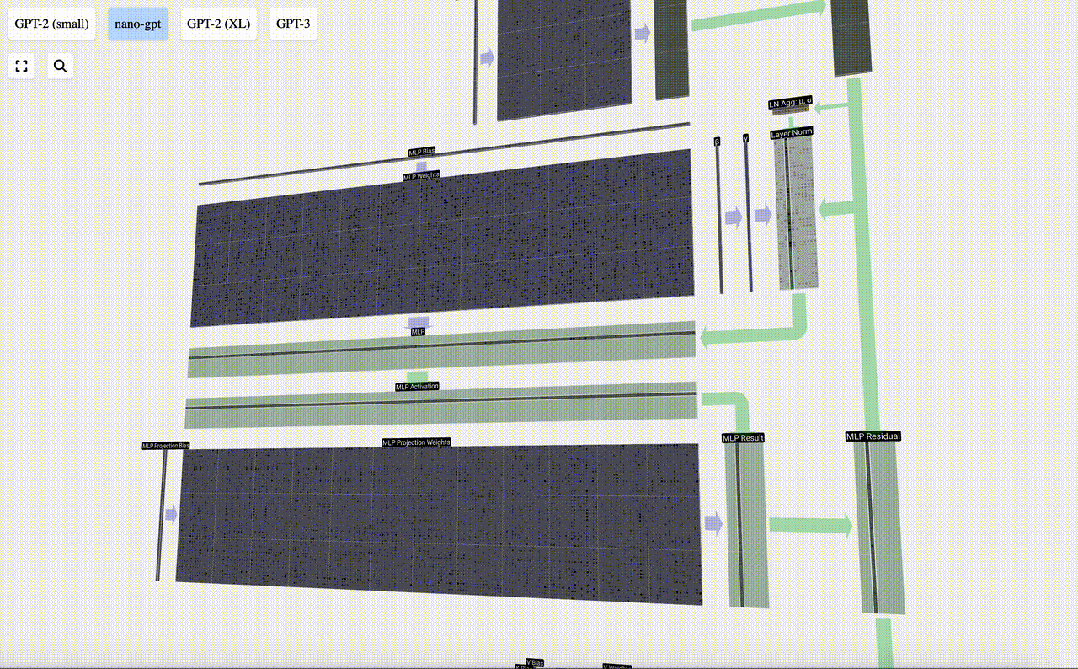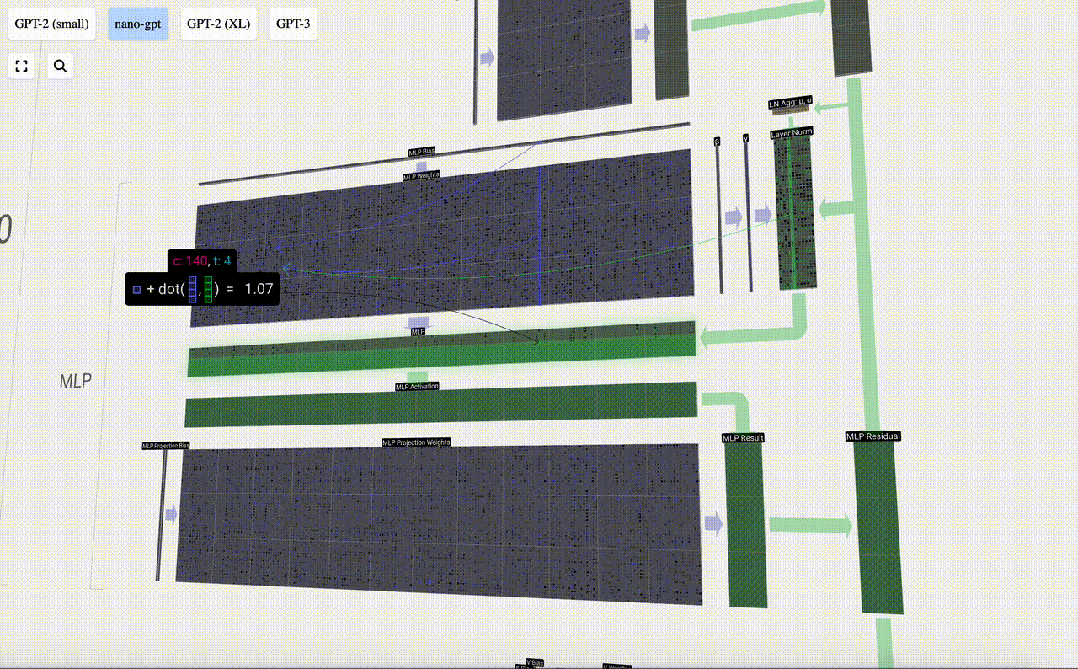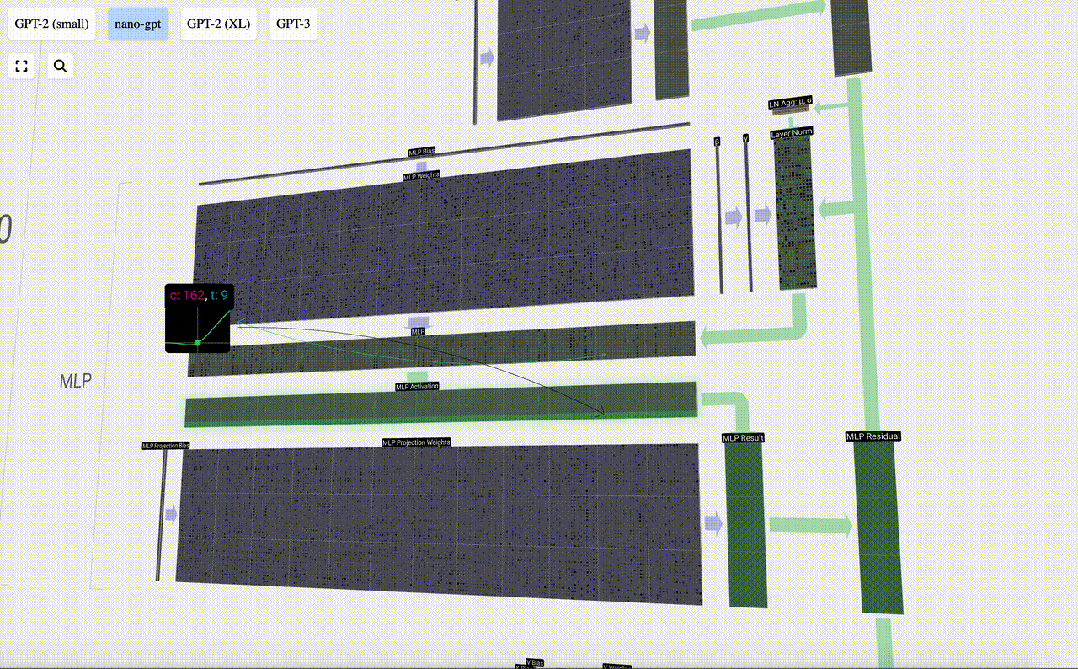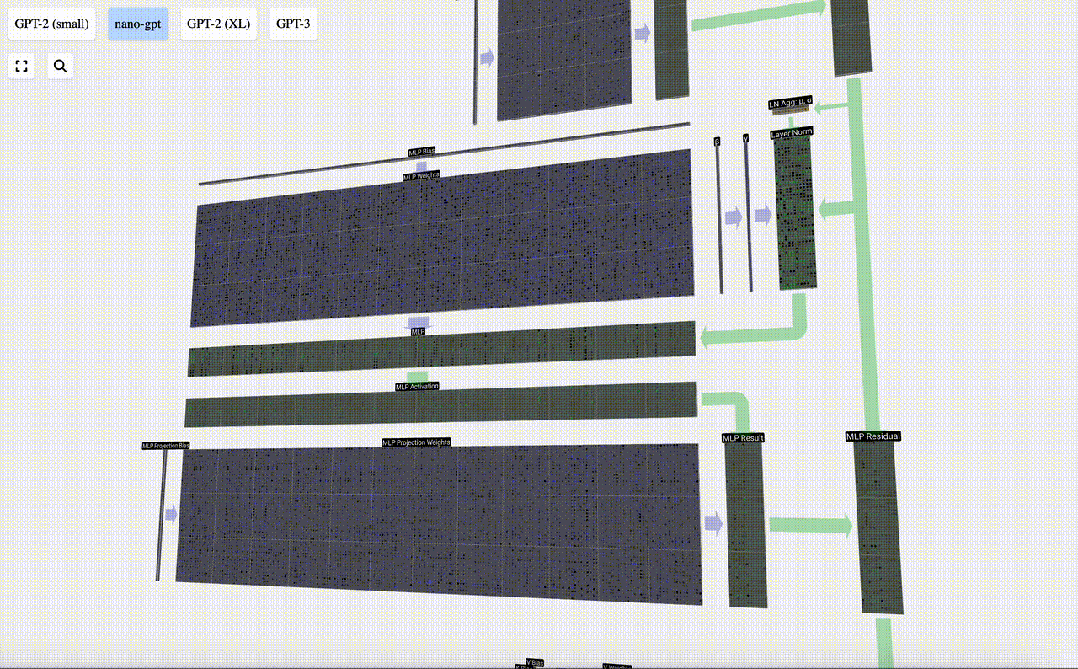
MLP層到此就結束了,我們最后也得到了transformer的輸出。
Transformer
這就是一個完整的Transformer模塊!
這些若干個模塊構成了任何 GPT 模型的主體,每個模塊的輸出都是下一個模塊的輸入。
正如在深度學習中常見的,很難準確說出這些層各自在做什么,但我們有一些大致的想法:較早的層傾向于專注于學習低級特征和模式,而后面的層則學習識別和理解更高級的抽象和關系。在自然語言處理的背景下,較低的層可能學習語法、句法和簡單的詞匯關聯,而較高的層可能捕捉更復雜的語義關系、話語結構和上下文依賴的含義。
Softmax
最后就是softmax操作,輸出每個token的預測概率。
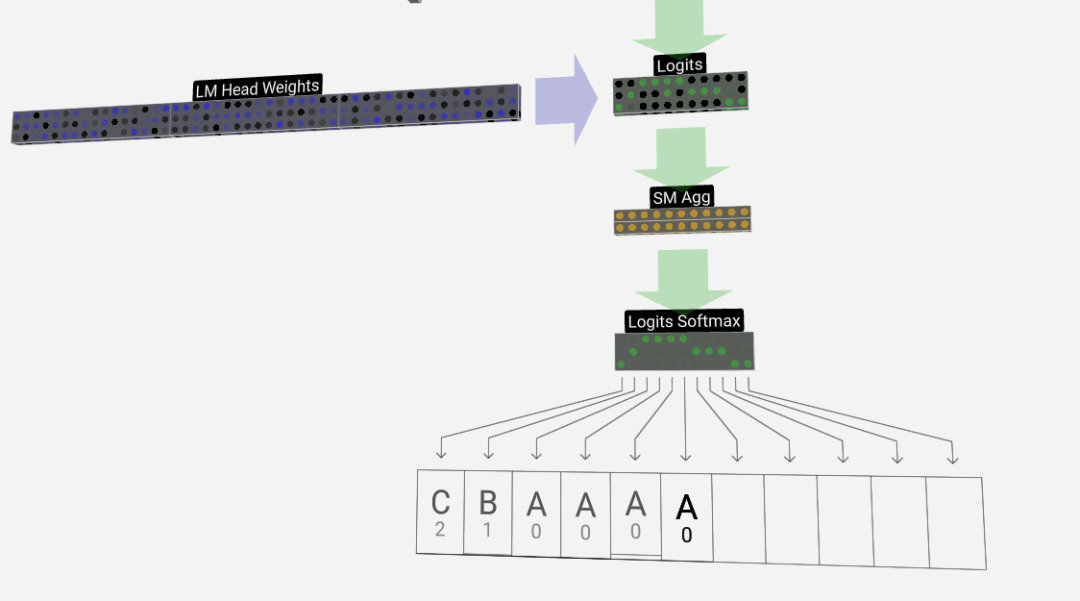
輸出Output
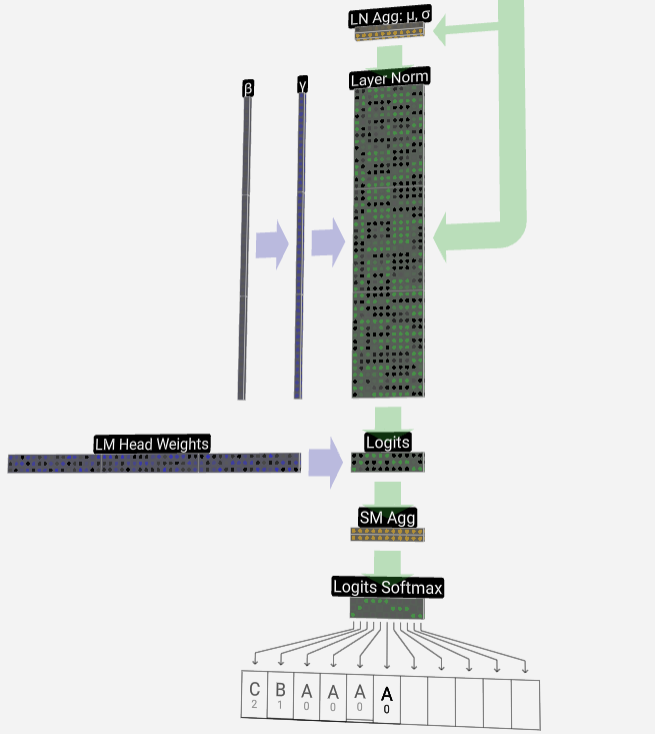
最終,我們到達了模型的尾端。最后一個Transfomer的輸出經過一層正則化處理,隨后進行一次無偏置的線性變換。
這一最終變換將我們的每個列向量從長度C轉換為詞匯量大小的長度nvocab。因此,它實際上是為詞匯表中的每個單詞生成一個得分logits。
為了將這些得分轉換為更加直觀的概率值,需要先通過softmax來進行處理。如此一來,對于每一列,我們都得到了模型分配給詞匯表中每個單詞的概率。
在這個特定模型中,它實際上已經學會了所有關于如何對三個字母進行排序的答案,因此概率極大地傾向于正確答案。
當我們讓模型隨時間推進時,需要使用最后一列的概率來決定序列中下一個添加的token。例如,如果我們向模型中輸入了六個token ,我們會使用第六列的輸出概率。
這一列的輸出是一系列概率值,我們實際上需要從中選出一個作為序列中的下一個token 。我們通過「從分布中采樣」來實現這一點,即根據其概率隨機選擇一個token 。例如,概率為0.9的token會被選擇的概率是90%。然而,我們也有其他選擇,例如總是選擇概率最高的 token 。
我們還可以通過使用溫度參數來控制分布的「平滑度」。較高的溫度會使分布更均勻,而較低的溫度則會使其更集中于概率最高的token 。
我們通過在應用softmax之前,用溫度參數來調整logits(線性變換的輸出),因為softmax中的指數化對較大數值有顯著的放大效果,使所有數值更接近將減少這種效果。
 圖片
圖片