推薦系統(tǒng)自1992 年代誕生以來(lái), 到2024 年的今天已經(jīng)有32 年的發(fā)展歷程。在這幾十年的發(fā)展歷程中，各個(gè)互聯(lián)網(wǎng)和科技公司上線過(guò)數(shù)以百萬(wàn)計(jì)的推薦系統(tǒng)模型。盡管推薦系統(tǒng)經(jīng)歷過(guò) 2012 到 2014 年的發(fā)展低潮，但很快就被后起之秀快手和字節(jié)跳動(dòng)一改頹勢(shì)，從而重新成為了熱點(diǎn)技術(shù)。在經(jīng)歷過(guò)淺層學(xué)習(xí)和深度學(xué)習(xí)之后，推薦系統(tǒng)的研究方向目前在往多元化方向發(fā)展，包括公平性和序列推薦等等。

推薦系統(tǒng)的經(jīng)典算法非常多，從早期的淺層學(xué)習(xí)算法協(xié)同過(guò)濾，到矩陣分解和線性模型，再到后面的深度學(xué)習(xí)和序列推薦，每一個(gè)發(fā)展時(shí)期都見(jiàn)證了某幾個(gè)里程碑算法贏家通吃的現(xiàn)象。推薦系統(tǒng)的技術(shù)這么成熟，還會(huì)有什么我們平常不留心的知識(shí)嗎？你別說(shuō)，還真有。不信請(qǐng)看本文：

1、什么？協(xié)同過(guò)濾算法在我的數(shù)據(jù)集合上有可能不成立？

是的，有可能。在 2023 年召開(kāi)的國(guó)際學(xué)術(shù)會(huì)議 CECNet 2023 上，研究人員發(fā)表了一篇題為 “Collaborative Filtering is a Lie or Not ? It Depends on the Shape of Your Domain” 的論文。這篇論文指出，協(xié)同過(guò)濾在某些數(shù)據(jù)集合上可能不成立。

作者首先利用任意一種降維算法，使用相似度矩陣推導(dǎo)的距離矩陣將用戶－用戶關(guān)系映射到二維空間。然后在點(diǎn) i 處定義 N （N 是和用戶 i 相似的用戶個(gè)數(shù)）個(gè)尾部在點(diǎn) i 坐標(biāo)的向量，每個(gè)向量為（Sim(i,j)-C, Sim(i,j)-C）, 其中 Sim(i,j) 為用戶 i 和用戶 j 之間的相似度，而 C 為任意實(shí)數(shù)。

我們根據(jù)推薦系統(tǒng)的預(yù)測(cè)評(píng)分是實(shí)數(shù)的特點(diǎn)，認(rèn)為在這些離散點(diǎn)之間存在著許多其他點(diǎn)，使得我們定義的向量場(chǎng)成立。

根據(jù) Poincare-Hopf Theorem ，如果一個(gè)向量場(chǎng)是定義在一個(gè)有向和緊致的流形上時(shí)，這個(gè)向量的零點(diǎn)的數(shù)量只和流形本身的歐拉示性數(shù)有關(guān)，而向量場(chǎng)本身無(wú)關(guān)。所以，如果我們降維下來(lái)的這個(gè)二維空間數(shù)據(jù)集合，滿足特定性質(zhì)，則協(xié)同過(guò)濾算法是不成立的。意不意外？驚不驚喜？

2、什么？矩陣分解算法中的先驗(yàn)概率不是高斯分布？

是的，矩陣分解算法中的先驗(yàn)概率不是高斯分布，是錐形分布。

研究人員在國(guó)際學(xué)術(shù)會(huì)議 CAMMIC 2023 上發(fā)表了一篇題為 “Analysis and visualization of the parameter space of matrix factorization-based recommender systems”的論文，對(duì)矩陣分解算法中的用戶向量矩陣和物品向量矩陣進(jìn)行了 Henze-Zirkler 檢驗(yàn)，發(fā)現(xiàn)矩陣分解算法中用戶向量和物品向量的先驗(yàn)分布不是高斯分布。作者隨后把這些向量進(jìn)行了可視化，得到了下圖：

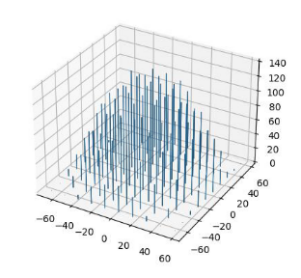
圖 1 用戶向量分布

圖 2 物品向量分布

通過(guò)觀察可視化結(jié)果，并通過(guò)邏輯分析，我們得到如下結(jié)論：矩陣分解算法中的先驗(yàn)概率是錐形分布，不是高斯分布。

3、什么？推薦系統(tǒng)評(píng)分?jǐn)?shù)據(jù)的長(zhǎng)尾現(xiàn)象可以用泊松過(guò)程建模？

是的，可以。我們可以通過(guò)如下關(guān)系對(duì)推薦系統(tǒng)的用戶評(píng)分進(jìn)行建模，我們姑且稱它為推薦系統(tǒng)中的齊夫分布：

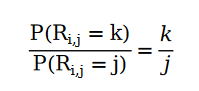
打個(gè)比方。在電影評(píng)分網(wǎng)站中，口碑 5 星的電影的評(píng)分?jǐn)?shù)量為 5；口碑 4 星的電影的評(píng)分?jǐn)?shù)量為 4 …… 我們發(fā)現(xiàn)，如果我們用Non-homogeneous Poisson Process 給用戶打分行為進(jìn)行建模之后，能夠通過(guò)解方程的形式得到符合評(píng)分滿足齊夫分布的解。

在 2023 年召開(kāi)的國(guó)際學(xué)術(shù)會(huì)議 CAMMIC 2023 上，研究人員發(fā)表了一篇題為 “Evolution of the Online Rating Platform Data Structures and its Implications for Recommender Systems”，詳細(xì)敘述了這一建模過(guò)程。

4、什么？推薦系統(tǒng)可以完全不利用任何數(shù)據(jù)解決冷啟動(dòng)問(wèn)題？

推薦系統(tǒng)中的冷啟動(dòng)問(wèn)題一直是個(gè)老大難問(wèn)題。傳統(tǒng)的解決方案無(wú)外乎 Transfer Learning / Meta Learning 或者熱點(diǎn)推薦。但是從 2021 年開(kāi)始到 2023 年出現(xiàn)了一系列的無(wú)需 Transfer Learning / Meta Learning 解決推薦系統(tǒng)冷啟動(dòng)的零樣本學(xué)習(xí)算法：ZeroMat、DotMat、RankMat、PoissonMat 和LogitMat。這些算法，無(wú)一例外的都不需要使用任何數(shù)據(jù)，就能取得比肩使用全量數(shù)據(jù)的矩陣分解算法的效果。

下面我們看兩張來(lái)自 LogitMat 原始論文的實(shí)驗(yàn)數(shù)據(jù)（MovieLens 1 Million Dataset）圖片：

圖 3 MAE 對(duì)比實(shí)驗(yàn)

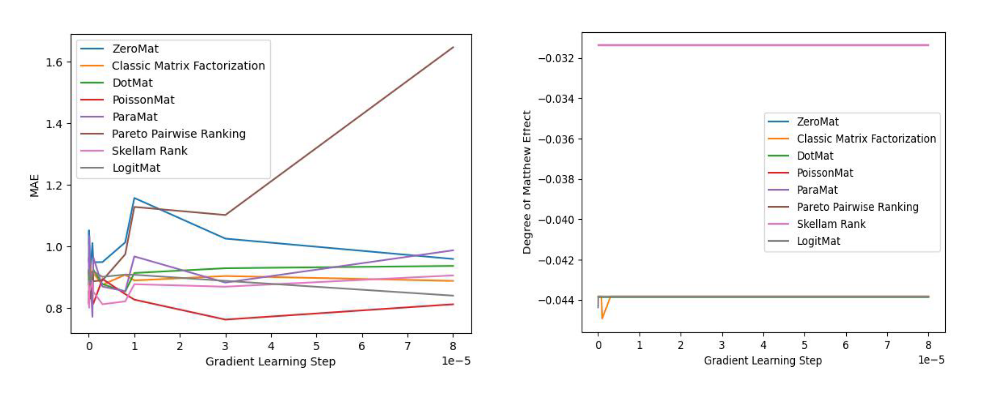
圖 4 公平性對(duì)比實(shí)驗(yàn)

通過(guò)觀察實(shí)驗(yàn)結(jié)果，我們發(fā)現(xiàn)這些算法無(wú)一例外的都可以比肩全樣本算法，甚至取得更好的效果。

5、什么？矩陣分解+正則化可以在 MovieLens 數(shù)據(jù)集上做到 MAE 0.6？

是的，可以。推薦系統(tǒng)的從業(yè)人員特別喜歡用 MovieLens 數(shù)據(jù)集測(cè)試自己的算法，然而歷史上的算法的 MAE 值通常都在 0.7 和 0.8 之間。其實(shí)，只要通過(guò)更改一下正則化項(xiàng)的懲罰函數(shù)的定義方式，就可以將 MAE 降到 0.6。下面我們來(lái)看一下研究人員是怎樣通過(guò)更改正則化項(xiàng)來(lái)優(yōu)化矩陣分解算法的：

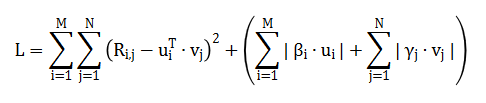
通過(guò)隨機(jī)梯度下降對(duì)損失函數(shù) L 求解，得到如下公式：

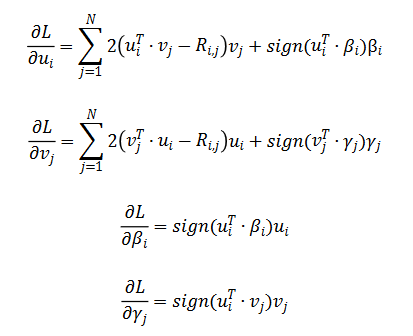
我們通過(guò)在 MovieLens Small Dataset 上做實(shí)驗(yàn)，發(fā)現(xiàn)通過(guò)修改矩陣分解的正則化項(xiàng)，可以將 MAE 降到 0.62 :

圖 3 MAE 對(duì)比實(shí)驗(yàn)圖                                                     4 公平性對(duì)比實(shí)驗(yàn)

關(guān)于正則化的這項(xiàng)新技術(shù)，可以參考學(xué)術(shù)論文 Theoretically Accurate Regularization Technique for Matrix Factorization based Recommender Systems 。

6、什么？推薦系統(tǒng)的結(jié)果還可以這樣可視化？

是的，我們可以對(duì)推薦系統(tǒng)進(jìn)行可視化。我們這里只舉一個(gè)例子：Takens Embedding。Takens Embedding 的細(xì)節(jié)我們不在這里敘述，我們這里只給出三張圖片，為讀者演示一下如何利用 Takens Embedding 對(duì)推薦系統(tǒng) MAE 曲線進(jìn)行升維，以便對(duì)推薦系統(tǒng)進(jìn)行可視化。具體的技術(shù)細(xì)節(jié)，可以參考學(xué)術(shù)論文 Effective Visualization and Analysis of Recommender Systems。

圖 5 MAE @ 1D

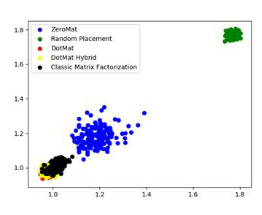
圖 6 MAE @ 2D

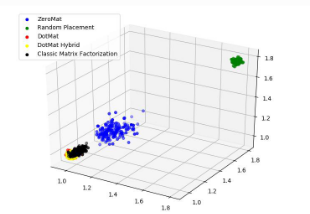
圖 7 MAE @ 3D

圖5、圖6 和 圖7展示了 MAE 曲線在 1D、2D 和 3D 空間的不同情況。2D 和 3D 空間的誤差點(diǎn)云可以更好的反映 MAE 的具體情況。

盡管推薦系統(tǒng)發(fā)展了許多年，但是我們每天仍然面臨著許多新的挑戰(zhàn)，仍然有數(shù)不勝數(shù)的新技術(shù)和新產(chǎn)品不斷出現(xiàn)，沖擊著我們的知識(shí)體系。因此，我們需要時(shí)刻保持著一顆年輕的和求知若渴的心態(tài)，這樣才能讓我們?cè)跁r(shí)代的大潮中保持著不敗的競(jìng)爭(zhēng)優(yōu)勢(shì)。

作者介紹

汪昊，前 Funplus 人工智能實(shí)驗(yàn)室負(fù)責(zé)人。曾在 ThoughtWorks、豆瓣、百度、新浪等公司擔(dān)任技術(shù)和技術(shù)高管職務(wù)。在互聯(lián)網(wǎng)公司和金融科技、游戲等公司任職 12 年，對(duì)于人工智能、計(jì)算機(jī)圖形學(xué)和區(qū)塊鏈等領(lǐng)域有著深刻的見(jiàn)解和豐富的經(jīng)驗(yàn)。在國(guó)際學(xué)術(shù)會(huì)議和期刊發(fā)表論文 42 篇，獲得IEEE SMI 2008 最佳論文獎(jiǎng)、ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 最佳論文報(bào)告獎(jiǎng)。