降維意味著我們在不丟失太多信息的情況下減少數(shù)據(jù)集中的特征數(shù)量，降維算法屬于無監(jiān)督學(xué)習(xí)的范疇，用未標(biāo)記的數(shù)據(jù)訓(xùn)練算法。

盡管降維方法種類繁多，但它們都可以歸為兩大類:線性和非線性。

線性方法將數(shù)據(jù)從高維空間線性投影到低維空間(因此稱為線性投影)。例子包括PCA和LDA。

非線性方法提供了一種執(zhí)行非線性降維(NLDR)的方法。我們經(jīng)常使用NLDR來發(fā)現(xiàn)原始數(shù)據(jù)的非線性結(jié)構(gòu)。當(dāng)原始數(shù)據(jù)不可線性分離時，NLDR很有用。在某些情況下，非線性降維也被稱為流形學(xué)習(xí)。

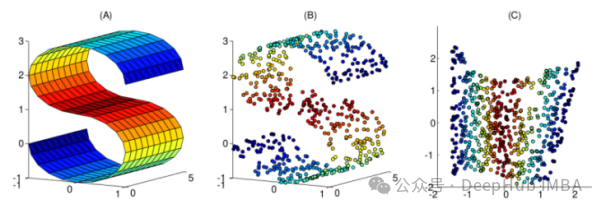
本文整理了10個常用的非線性降維技術(shù)，可以幫助你在日常工作中進行選擇

1、核PCA

你們可能熟悉正常的PCA，這是一種線性降維技術(shù)。核PCA可以看作是正態(tài)主成分分析的非線性版本。

常規(guī)主成分分析和核主成分分析都可以進行降維。但是核PCA能很好地處理線性不可分割的數(shù)據(jù)。因此，核PCA算法的主要用途是使線性不可分的數(shù)據(jù)線性可分，同時降低數(shù)據(jù)的維數(shù)!

我們先創(chuàng)建一個非常經(jīng)典的數(shù)據(jù)：

import matplotlib.pyplot as plt
 plt.figure(figsize=[7, 5])
 
 from sklearn.datasets import make_moons
 X, y = make_moons(n_samples=100, noise=None, 
                  random_state=0)
 
 plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='plasma')
 plt.title('Linearly inseparable data')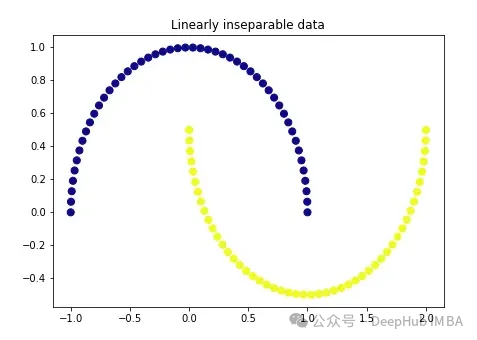

這兩種顏色代表線性上不可分割的兩類。我們不可能在這里畫一條直線把這兩類分開。

我們先使用常規(guī)PCA。

 import numpy as np
 from sklearn.decomposition import PCA
 
 pca = PCA(n_components=1)
 X_pca = pca.fit_transform(X)
 
 plt.figure(figsize=[7, 5])
 plt.scatter(X_pca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after linear PCA')
 plt.xlabel('PC1')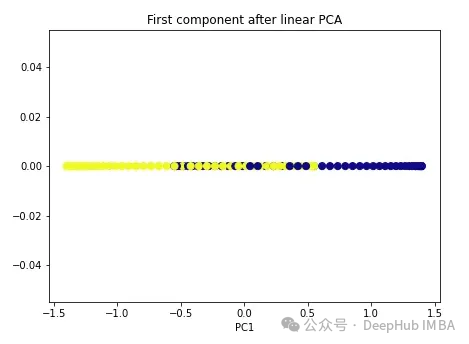

可以看到，這兩個類仍然是線性不可分割的，現(xiàn)在我們試試核PCA。

 import numpy as np
 from sklearn.decomposition import KernelPCA
 
 kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15)
 X_kpca = kpca.fit_transform(X)
 
 plt.figure(figsize=[7, 5])
 plt.scatter(X_kpca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.axvline(x=0.0, linestyle='dashed', color='black', linewidth=1.2)
 plt.title('First component after kernel PCA')
 plt.xlabel('PC1')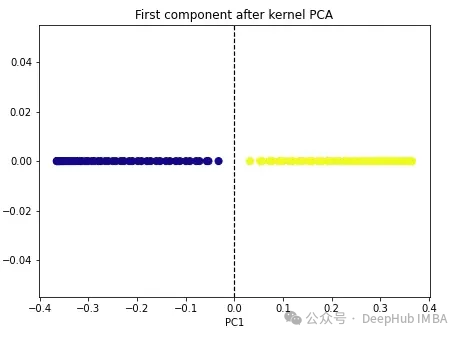

這兩個類變成了線性可分的，核PCA算法使用不同的核將數(shù)據(jù)從一種形式轉(zhuǎn)換為另一種形式。核PCA是一個兩步的過程。首先核函數(shù)暫時將原始數(shù)據(jù)投影到高維空間中，在高維空間中，類是線性可分的。然后算法將該數(shù)據(jù)投影回n_components超參數(shù)(我們想要保留的維數(shù))中指定的較低維度。

sklearn中有四個核選項:linear’, ‘poly’, ‘rbf’ and ‘sigmoid’。如果我們將核指定為“線性”，則將執(zhí)行正常的PCA。任何其他核將執(zhí)行非線性PCA。rbf(徑向基函數(shù))核是最常用的。

2、多維尺度變換(multidimensional scaling, MDS)

多維尺度變換是另一種非線性降維技術(shù)，它通過保持高維和低維數(shù)據(jù)點之間的距離來執(zhí)行降維。例如，原始維度中距離較近的點在低維形式中也顯得更近。

要在Scikit-learn我們可以使用MDS()類。

 from sklearn.manifold import MDS
 
 mds = MDS(n_components, metric)
 mds_transformed = mds.fit_transform(X)

metric 超參數(shù)區(qū)分了兩種類型的MDS算法:metric和non-metric。如果metric=True，則執(zhí)行metric MDS。否則，執(zhí)行non-metric MDS。

我們將兩種類型的MDS算法應(yīng)用于以下非線性數(shù)據(jù)。

 import numpy as np
 from sklearn.manifold import MDS
 
 mds = MDS(n_components=1, metric=True) # Metric MDS
 X_mds = mds.fit_transform(X)
 
 plt.figure(figsize=[7, 5])
 plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('Metric MDS')
 plt.xlabel('Component 1')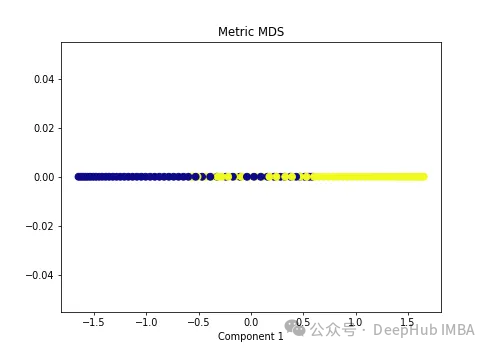

 import numpy as np
 from sklearn.manifold import MDS
 
 mds = MDS(n_components=1, metric=False) # Non-metric MDS
 X_mds = mds.fit_transform(X)
 
 plt.figure(figsize=[7, 5])
 plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('Non-metric MDS')
 plt.xlabel('Component 1')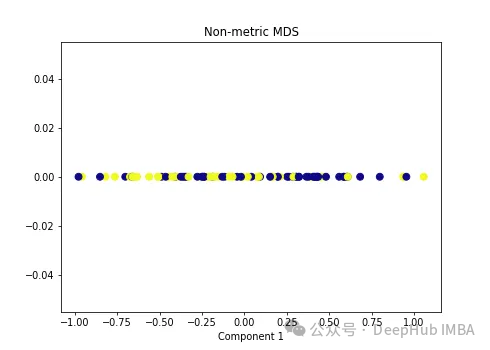

可以看到MDS后都不能使數(shù)據(jù)線性可分，所以可以說MDS不適合我們這個經(jīng)典的數(shù)據(jù)集。

3、Isomap

Isomap(Isometric Mapping)在保持?jǐn)?shù)據(jù)點之間的地理距離，即在原始高維空間中的測地線距離或者近似的測地線距離，在低維空間中也被保持。Isomap的基本思想是通過在高維空間中計算數(shù)據(jù)點之間的測地線距離(通過最短路徑算法，比如Dijkstra算法)，然后在低維空間中保持這些距離來進行降維。在這個過程中，Isomap利用了流形假設(shè)，即假設(shè)高維數(shù)據(jù)分布在一個低維流形上。因此，Isomap通常在處理非線性數(shù)據(jù)集時表現(xiàn)良好，尤其是當(dāng)數(shù)據(jù)集包含曲線和流形結(jié)構(gòu)時。

 import matplotlib.pyplot as plt
 plt.figure(figsize=[7, 5])
 
 from sklearn.datasets import make_moons
 X, y = make_moons(n_samples=100, noise=None, 
                  random_state=0)
 
 import numpy as np
 from sklearn.manifold import Isomap
 
 isomap = Isomap(n_neighbors=5, n_components=1)
 X_isomap = isomap.fit_transform(X)
 
 plt.figure(figsize=[7, 5])
 plt.scatter(X_isomap[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying Isomap')
 plt.xlabel('Component 1')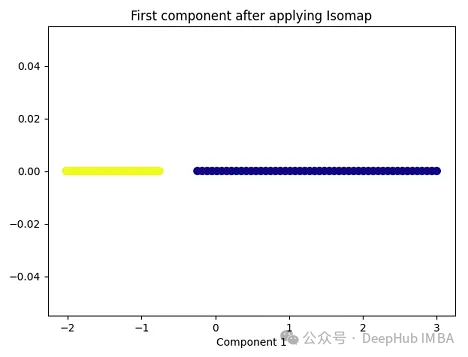

就像核PCA一樣，這兩個類在應(yīng)用Isomap后是線性可分的!

4、Locally Linear Embedding(LLE)

與Isomap類似，LLE也是基于流形假設(shè)，即假設(shè)高維數(shù)據(jù)分布在一個低維流形上。LLE的主要思想是在局部鄰域內(nèi)保持?jǐn)?shù)據(jù)點之間的線性關(guān)系，并在低維空間中重構(gòu)這些關(guān)系。

 from sklearn.manifold import LocallyLinearEmbedding
 lle = LocallyLinearEmbedding(n_neighbors=5,n_components=1)
 lle_transformed = lle.fit_transform(X)
 plt.figure(figsize=[7, 5])
 plt.scatter(lle_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying LocallyLinearEmbedding')
 plt.xlabel('Component 1')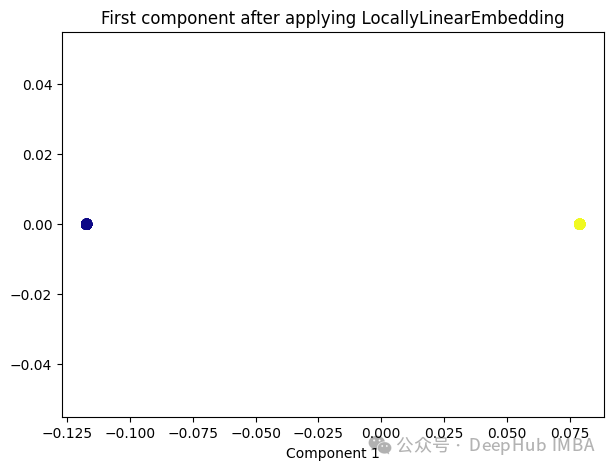

只有2個點，其實并不是這樣，我們打印下這個數(shù)據(jù)

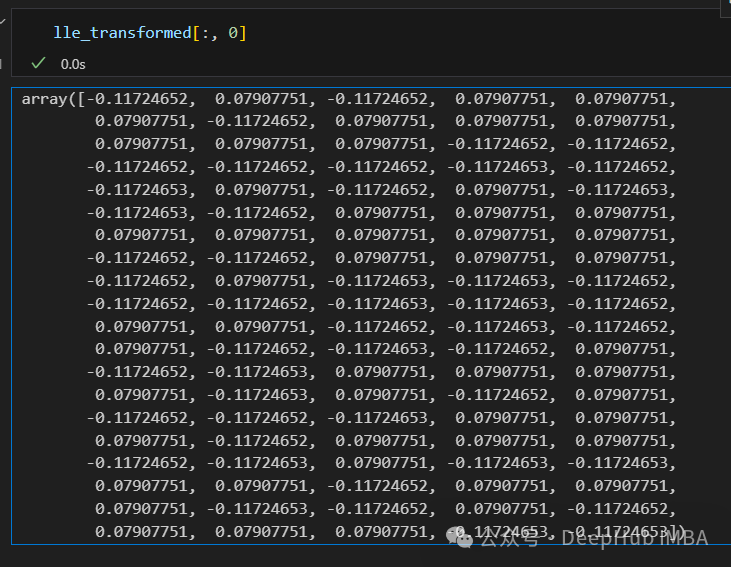
可以看到數(shù)據(jù)通過降維變成了同一個數(shù)字，所以LLE降維后是線性可分的，但是卻丟失了數(shù)據(jù)的信息。

5、Spectral Embedding

Spectral Embedding是一種基于圖論和譜理論的降維技術(shù)，通常用于將高維數(shù)據(jù)映射到低維空間。它的核心思想是利用數(shù)據(jù)的相似性結(jié)構(gòu)，將數(shù)據(jù)點表示為圖的節(jié)點，并通過圖的譜分解來獲取低維表示。

 from sklearn.manifold import SpectralEmbedding
 sp_emb = SpectralEmbedding(n_components=1, affinity='nearest_neighbors')
 sp_emb_transformed = sp_emb.fit_transform(X)
 plt.figure(figsize=[7, 5])
 plt.scatter(sp_emb_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying SpectralEmbedding')
 plt.xlabel('Component 1')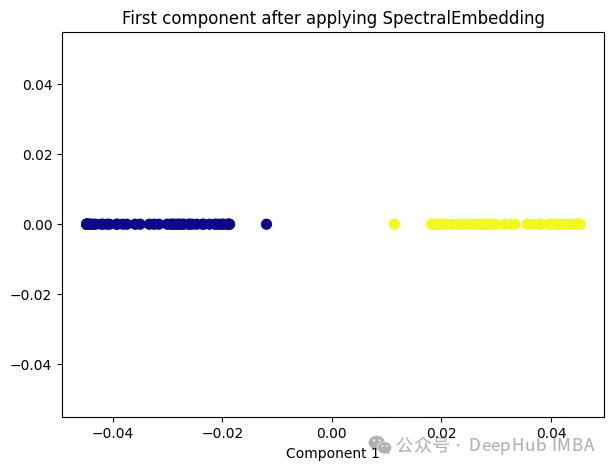

6、t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE的主要目標(biāo)是保持?jǐn)?shù)據(jù)點之間的局部相似性關(guān)系，并在低維空間中保持這些關(guān)系，同時試圖保持全局結(jié)構(gòu)。

from sklearn.manifold import TSNE
 tsne = TSNE(1, learning_rate='auto', init='pca')
 tsne_transformed = tsne.fit_transform(X)
 plt.figure(figsize=[7, 5])
 plt.scatter(tsne_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying TSNE')
 plt.xlabel('Component 1')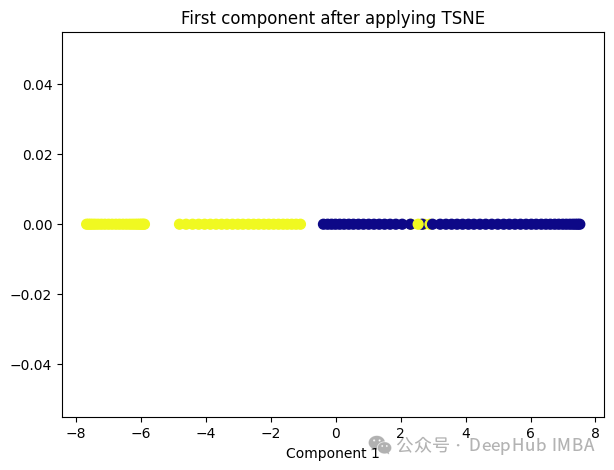

t-SNE好像也不太適合我們的數(shù)據(jù)。

7、Random Trees Embedding

Random Trees Embedding是一種基于樹的降維技術(shù)，常用于將高維數(shù)據(jù)映射到低維空間。它利用了隨機森林(Random Forest)的思想，通過構(gòu)建多棵隨機決策樹來實現(xiàn)降維。

Random Trees Embedding的基本工作流程：

• 構(gòu)建隨機決策樹集合：首先，構(gòu)建多棵隨機決策樹。每棵樹都是通過從原始數(shù)據(jù)中隨機選擇子集進行訓(xùn)練的，這樣可以減少過擬合，提高泛化能力。
• 提取特征表示：對于每個數(shù)據(jù)點，通過將其在每棵樹上的葉子節(jié)點的索引作為特征，構(gòu)建一個特征向量。每個葉子節(jié)點都代表了數(shù)據(jù)點在樹的某個分支上的位置。
• 降維：通過隨機森林中所有樹生成的特征向量，將數(shù)據(jù)點映射到低維空間中。通常使用降維技術(shù)，如主成分分析(PCA)或t-SNE等，來實現(xiàn)最終的降維過程。

Random Trees Embedding的優(yōu)勢在于它的計算效率高，特別是對于大規(guī)模數(shù)據(jù)集。由于使用了隨機森林的思想，它能夠很好地處理高維數(shù)據(jù)，并且不需要太多的調(diào)參過程。

RandomTreesEmbedding使用高維稀疏進行無監(jiān)督轉(zhuǎn)換，也就是說，我們最終得到的數(shù)據(jù)并不是一個連續(xù)的數(shù)值，而是稀疏的表示。所以這里就不進行代碼展示了，有興趣的看看sklearn的sklearn.ensemble.RandomTreesEmbedding

8、Dictionary Learning

Dictionary Learning是一種用于降維和特征提取的技術(shù)，它主要用于處理高維數(shù)據(jù)。它的目標(biāo)是學(xué)習(xí)一個字典，該字典由一組原子(或基向量)組成，這些原子是數(shù)據(jù)的線性組合。通過學(xué)習(xí)這樣的字典，可以將高維數(shù)據(jù)表示為一個更緊湊的低維空間中的稀疏線性組合。

Dictionary Learning的優(yōu)點之一是它能夠?qū)W習(xí)出具有可解釋性的原子，這些原子可以提供關(guān)于數(shù)據(jù)結(jié)構(gòu)和特征的重要見解。此外，Dictionary Learning還可以產(chǎn)生稀疏表示，從而提供更緊湊的數(shù)據(jù)表示，有助于降低存儲成本和計算復(fù)雜度。

 from sklearn.decomposition import DictionaryLearning
 
 dict_lr = DictionaryLearning(n_components=1)
 dict_lr_transformed = dict_lr.fit_transform(X)
 plt.figure(figsize=[7, 5])
 plt.scatter(dict_lr_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying DictionaryLearning')
 plt.xlabel('Component 1')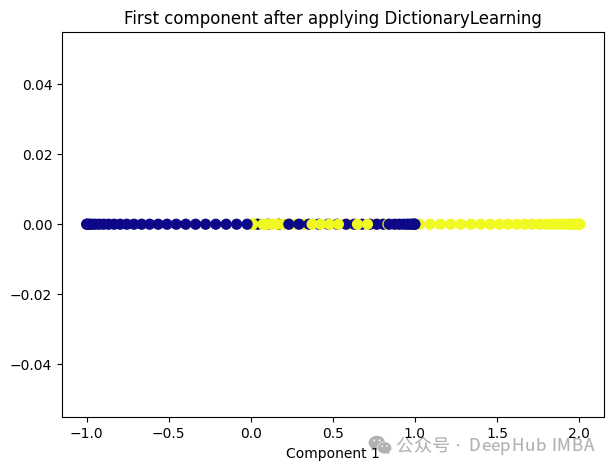

9、Independent Component Analysis (ICA)

Independent Component Analysis (ICA) 是一種用于盲源分離的統(tǒng)計方法，通常用于從混合信號中估計原始信號。在機器學(xué)習(xí)和信號處理領(lǐng)域，ICA經(jīng)常用于解決以下問題：

• 盲源分離：給定一組混合信號，其中每個信號是一組原始信號的線性組合，ICA的目標(biāo)是從混合信號中分離出原始信號，而不需要事先知道混合過程的具體細(xì)節(jié)。
• 特征提取：ICA可以被用來發(fā)現(xiàn)數(shù)據(jù)中的獨立成分，提取數(shù)據(jù)的潛在結(jié)構(gòu)和特征，通常在降維或預(yù)處理過程中使用。

ICA的基本假設(shè)是，混合信號中的各個成分是相互獨立的，即它們的統(tǒng)計特性是獨立的。這與主成分分析(PCA)不同，PCA假設(shè)成分之間是正交的，而不是獨立的。因此ICA通常比PCA更適用于發(fā)現(xiàn)非高斯分布的獨立成分。

 from sklearn.decomposition import FastICA
 
 ica = FastICA(n_components=1, whiten='unit-variance')
 ica_transformed = dict_lr.fit_transform(X)
 plt.figure(figsize=[7, 5])
 plt.scatter(ica_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')
 plt.title('First component after applying FastICA')
 plt.xlabel('Component 1')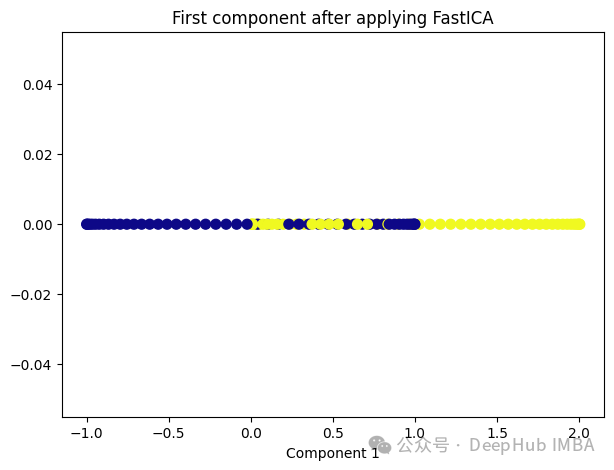

10、Autoencoders (AEs)

到目前為止，我們討論的NLDR技術(shù)屬于通用機器學(xué)習(xí)算法的范疇。而自編碼器是一種基于神經(jīng)網(wǎng)絡(luò)的NLDR技術(shù)，可以很好地處理大型非線性數(shù)據(jù)。當(dāng)數(shù)據(jù)集較小時，自動編碼器的效果可能不是很好。

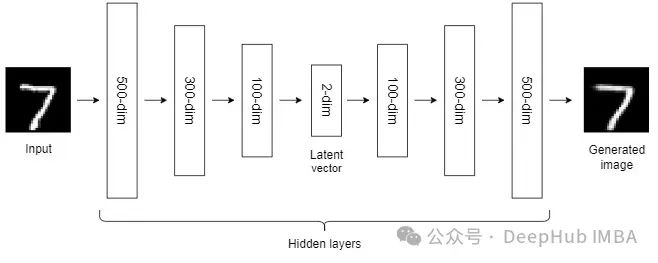
自編碼器我們已經(jīng)介紹過很多次了，所以這里就不詳細(xì)說明了。

總結(jié)

非線性降維技術(shù)是一類用于將高維數(shù)據(jù)映射到低維空間的方法，它們通常適用于數(shù)據(jù)具有非線性結(jié)構(gòu)的情況。

大多數(shù)NLDR方法基于最近鄰方法，該方法要求數(shù)據(jù)中所有特征的尺度相同，所以如果特征的尺度不同，還需要進行縮放。

另外這些非線性降維技術(shù)在不同的數(shù)據(jù)集和任務(wù)中可能表現(xiàn)出不同的性能，因此在選擇合適的方法時需要考慮數(shù)據(jù)的特征、降維的目標(biāo)以及計算資源等因素。