預測中的不確定性對于決策者了解潛在結果和相關風險的范圍非常重要。通過量化不確定性，企業可以做出更明智的決策，并有效地分配資源。關于預測的不確定性，前面有"用于時間序列概率預測的定量回歸“ 和 ”時間序列概率預測的共形預測“的介紹。本文將介紹另一項重要技術--共形分位數回歸（CQR）。共形分位數回歸（CQR）結合了分位數回歸（QR）和共形預測（CP），使兩者相輔相成。

分位數回歸 QR

QR 估算的是目標變量的條件量值，如中位數或第 90 個百分位數，而不是條件均值。通過分別估計不同水平預測變量的條件量值，可以很好地處理異方差。雖然大多數情況下量化值可以提供準確的預測區間，但當模型假設被違反時，量化值預測可能會不準確。

共形預測 CP

另一方面，CP 能確保預測區間中的實際值，而無需明確關注特定的量化值。它根據實際數據而非任何模型規范形成預測區間。對所有數據范圍都會產生一個固定的寬度。

共形分位數回歸CQR

為什么不同時使用 QR 和 CP 呢？共形分位數回歸（CQR）技術提供了一個值得稱贊的解決方案，可以提供具有有效覆蓋保證的預測區間。這些覆蓋保證是由量回歸產生的。CQR 調整了預測區間，以確保實際值總是落在預測區間內，并達到所需的置信水平。

什么是CQR

CQR（Conformal Quantile Regression）的基本思想是建立分位數回歸（QR）模型用于預測區間，并使用CP技術進行調整。上一章中介紹了CP如何建立預測區間，通過獲取點預測值與實際值之間的誤差得出容差區間，然后將其與點估計值相連形成預測區間。然而，QR已經給出了預測區間。要調整預測區間，我們需要修改CP方法為CQR，因為在量化預測中，CP以點預測為中心，而應用于預測區間的CQR則以預測區間的兩個錨點（下限和上限）為中心。

CQR的發展過程稱為一致性得分。符合性得分涉及實際值與預測區間上下限之間的距離。如果實際值持續高于上限或下限，則應根據一致性得分調整預測區間，確保在選定的時間水平下，實際值在預測區間內。一致性得分是大括號中兩個項中較大的一項。

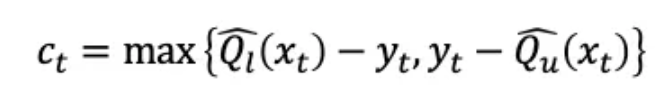公式（1）

其中，yt是實際值，Ql和Qu是低量化值和高量化值（下限和上限），ct是符合性得分

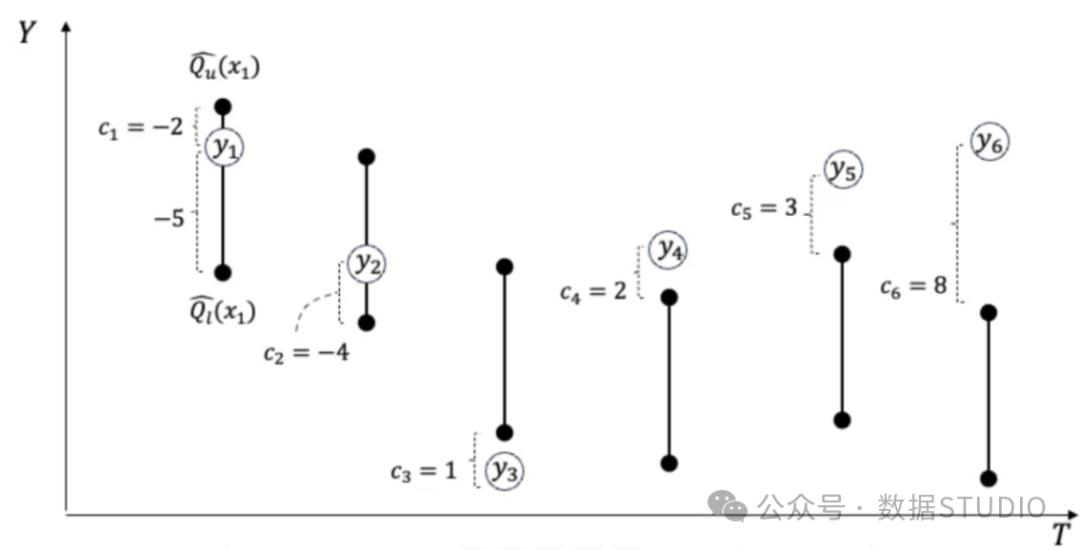
我們以圖(A)中的示例來解釋等式(1)。假設有六個實際值y1至y6及其相應的預測區間。在第一次預測中，實際值y1的預測區間在下限Ql和上限Qu之間，而y1更接近上限QU。每個預測區間都會有一個一致性得分。根據公式(1)，第一個預測值c1的一致性分值為-2，處于-2和-5之間。當y在預測區間內時，一致性總是負數，而當實際值在預測區間外時，一致性總是正數。

圖(A)：一致性得分

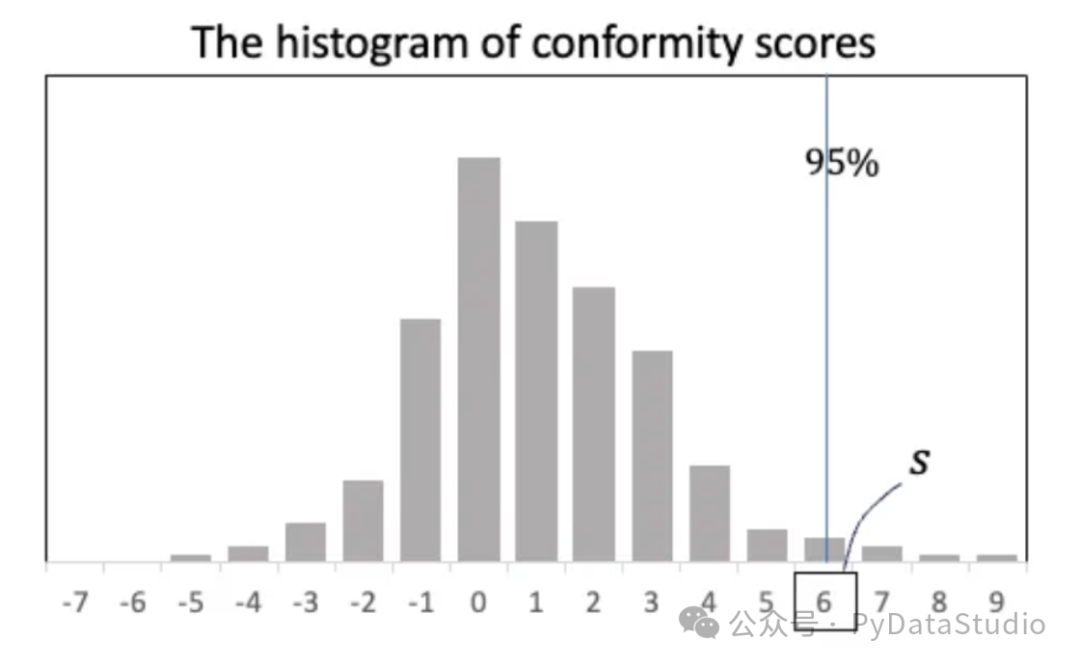
我們將為一致性得分繪制一個直方圖，如圖（B）所示。左側的負分表示實際值在預測區間內。右側的正分數表示預測區間無法捕捉實際值。

圖(B)：一致性得分直方圖

可以根據容忍度確定一個閾值s。根據圖(B)，95% 一致性得分是 6.0。預測區間將會擴大，保證實際值包含在預測區間內。

形式上，CQR 根據下面的公式 (2) 調整分位數回歸的預測區間。它從下限Ql中減去閾值s，再將閾值s加到上限QU：

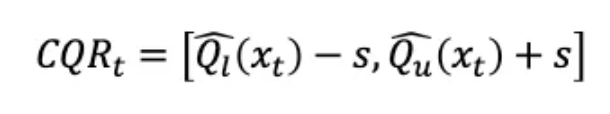公式（2）

一致性得分可為負，表示所有預測區間均包含實際值。在這種情況下，符合性得分的加減可能導致預測區間變短。CQR 會根據 QR 在區間內的表現調整預測區間，對于始終低估或高估的 QR 會做出相應調整。

CQR 的構建

其過程可概括如下：

• 首先，我們將歷史時間序列數據分為訓練期、校準期和測試期。
• 然后在訓練數據上訓練分位數回歸模型。應用訓練模型生成校準數據的量化預測。
• 然后根據公式 (1) 計算一致性得分。繪制符合性得分直方圖，以定義容差水平，如圖 (B)。
• 然后根據公式 (2) 調整不同量化值的預測區間。

環境要求

NeuralProphet 有三個選項：(i) 分位數回歸 (QR)(ii) 保形預測 (CP)(iii) 保形分位數回歸 (CQR)，用于處理預測的不確定性。

!pip install neuralprophet
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

數據

%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")

data = pd.read_csv('/bike_sharing_daily.csv')
# 數據獲取：公眾號：數據STUDIO 后臺回復 云朵君
data.tail()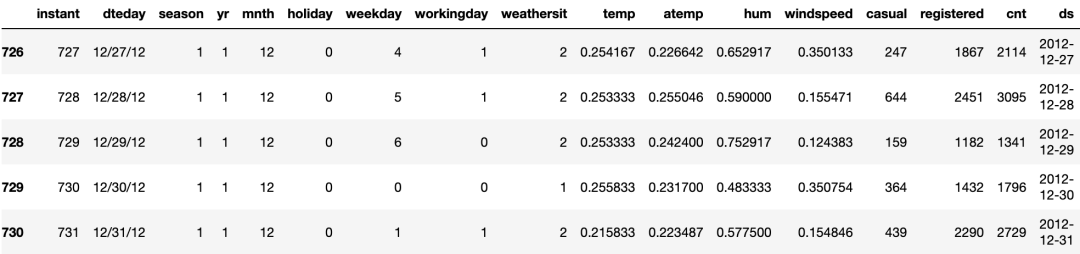

圖(C)：自行車租賃數據

數據集包含每日租賃需求、天氣信息（如溫度和風速）等多變量數據。在進行建模之前，需要對數據進行最基本的準備。NeuralProphet 要求列名為ds和y。

# convert string to datetime64
data["ds"] = pd.to_datetime(data["dteday"])
df = data[['ds','cnt']]
df.columns = ['ds','y']

建模

使用具有趨勢和季節性模式的NeuralProphet模型，可以添加其他組件，如AR、假期和其他協變量。目前代碼已進行了注釋。

from neuralprophet import NeuralProphet
quantile_list=[0.05,0.95 ]
# Model and prediction
cqr_model = NeuralProphet(
    quantiles=quantile_list,
    #n_changepoints=10,
    yearly_seasnotallow=True,
    weekly_seasnotallow=True,
    daily_seasnotallow=False,
    # Add the autogression
    #n_lags=10,
    # Forecast the next 50 days
    #n_forecasts= 50
)
cqr_model = cqr_model.add_country_holidays("US")
#cqr_model.set_plotting_backend("matplotlib")  # Use matplotlib

訓練、驗證和測試數據

共形分位數回歸的一個關鍵步驟是將訓練數據分為訓練數據和校準數據，用于構建符合性得分。

df_train, df_test = cqr_model.split_df(df, valid_p=0.2)
df_train, df_cal = cqr_model.split_df(df_train, freq="D", valid_p=1.0 / 11)
[df_train.shape, df_test.shape, df_cal.shape]
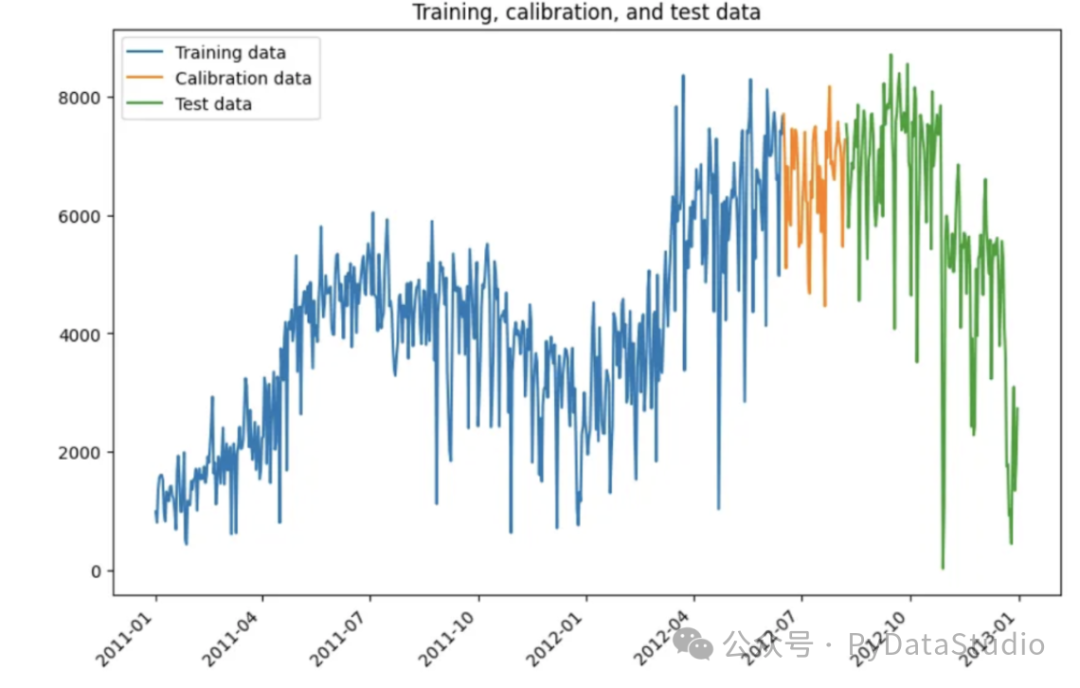
# [(532, 2), (146, 2), (53, 2)]

用三種顏色繪制不同的數據集。

圖（D）

驗證數據作為模型驗證集。

metrics = cpr_model.fit(df_train, validation_df=df_cal, progress="bar")
metrics.tail()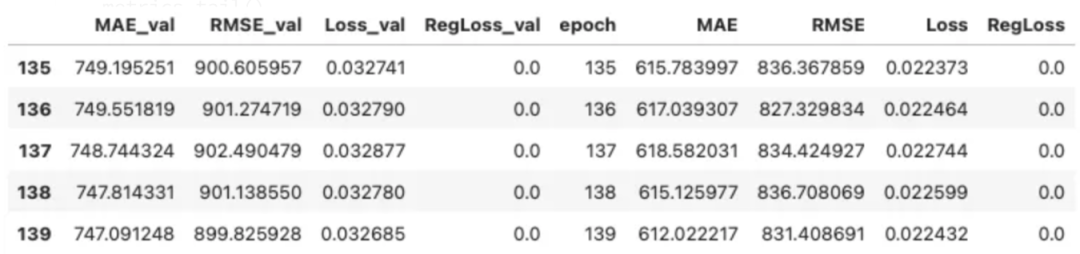

圖片

共形分位數回歸

創建一個future數據集，在df數據的最后日期之后有50個周期。它將包括所有歷史數據的模型預測。或者，如果指定n_historic_predictinotallow=40，它將只包含40個歷史數據點及其預測結果。

NeuralProphet 的 CQR 選項是method=cqr。我們將通過.conformal_prediction()啟用保形預測。

future = cpr_model.make_future_dataframe(df, periods=50, 
     n_historic_predictinotallow=True)

# Parameter for CQR
method = "cqr"
alpha = 0.05
# Enable conformal prediction on the pre-trained models
cqr_forecast = cqr_model.conformal_predict(
    # df_test, # You can also use df_test
    future,
    calibration_df=df_cal,
    alpha=alpha,
    method=method,
    show_all_PI=True,
)
cqr_forecast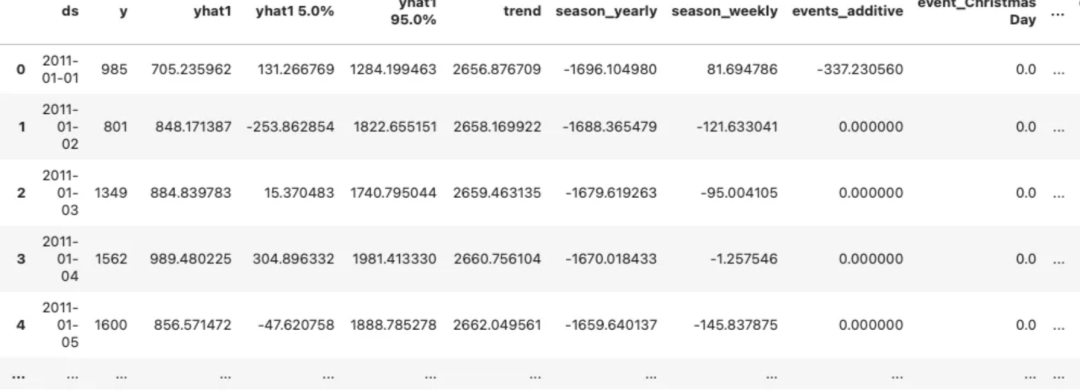

圖片

繪制預測結果和預測區間圖。CQR 預測區間寬度變化。在圖（E）中，95% 的情況下，實際值都在預測區間內，因為 CP 可以確保實際值在預測區間內的時間為95%。

fig = cqr_model.plot(cqr_forecast, 
    #plotting_backend = "matplotlib"
    plotting_backend="plotly-static"
)

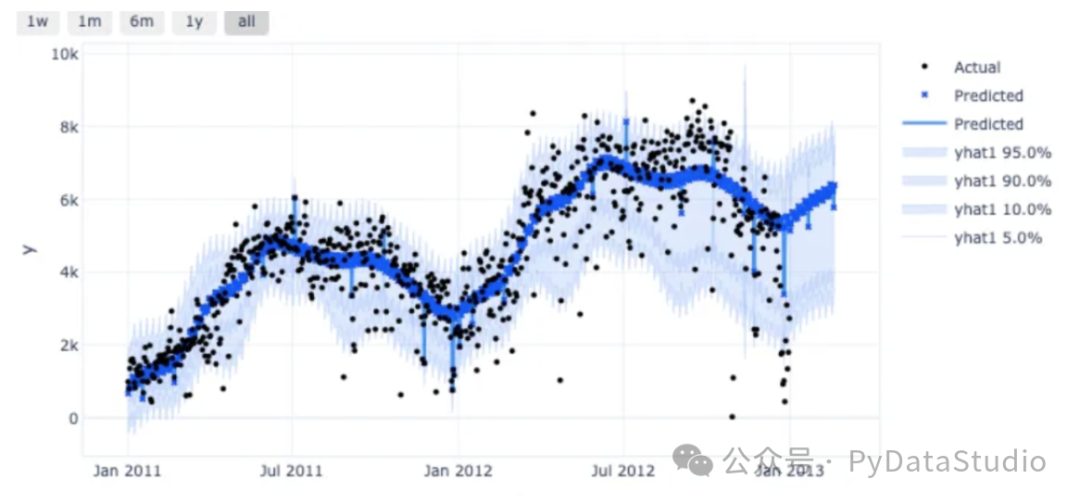圖（E）