73年前,香農已經給大模型發展埋下一顆種子
當今 AI 領域爆火的大語言模型(LLM),其原理是香農提出來的?
今天,普林斯頓大學教授承現峻(Sebastian Seung)拋出了這樣一個觀點:1951 年,在貝爾實驗室(總部位于新澤西州 Murray Hill)工作的克勞德?香農提出了預測下一個單詞的問題,這成為了當前大語言模型(LLM)的種子。
如今很多看似新潮前沿的概念,其實距離提出已經相隔了好幾十年,即使在計算機科學這樣的新興領域,例子也屢見不鮮。這個觀點以及提到的 Murray Hill 引起熱議,圖靈獎得主、Meta 首席科學家 LeCun 表示,新澤西州的 Murray Hill、Florham Park 和普林斯頓都「誕生」了很多有影響力的工作。
LeCun 又列舉了很多知名的研究成果:
- Hopfield 網絡(美國科學家 Hopfield 同時在貝爾實驗室和普林斯頓大學任職)。
- ConvNets
- Boosting/Adaboost
- 非負矩陣分解
- 支持向量機(SVM)和核機
- 結構化預測
- 計算學習理論 / VC 理論中的大量內容

那么說在這其中,香農給如今通向 AGI 的大模型起了個頭,是怎么一回事呢?
討論中提到的 IT 祖師爺克勞德?香農的論文是《Prediction and Entropy of Printed English》。

論文鏈接:https://www.princeton.edu/~wbialek/rome/refs/shannon_51.pdf
該研究于 1951 年 1 月發表在期刊《The Bell System Technical Journal》上,至今已被各路學者引用過超過 4000 次。
這篇論文中,香農主要探討了如何估算語言的熵(entropy)和冗余度(redundancy),并提出了一種新方法。
其中:
- 語言的熵是衡量每個字母平均產生的信息量的統計參數。如果語言被最有效地轉換成二進制數字(0 或 1),熵表示每個字母平均需要的二進制數字數量。
- 冗余度則衡量由于語言的統計結構(如字母頻率、特定字母的后續趨勢等)對文本施加的約束。
在定義了熵和冗余之后,就可以考慮把這些概念應用一下了。香農在他的論文中給出了兩種估計英語熵的方法。冗余,或對英語文本施加的約束數量,導致其整體熵的下降。例如,規則「i before e except after c」,以及 q 必須始終跟 u 的事實是使英語更加冗余的依賴關系。語法規則、詞性以及我們無法編造單詞的事實也使英語變得有冗余。
英語中的冗余有時實際上是有益的,因為否則人們如何辨別在嘈雜的房間里說了什么?冗余允許人們在只有部分信息傳來時推斷出所說的內容。例如,如果聽到「Turn phat mufic down!」,人們可以相當好地猜測說話者的意思。
計算英語熵的一種可能方法是使用 N-gram。
給定自然語言 L 的足夠長的字符序列 S,考察所有長度為 N 的子字符串
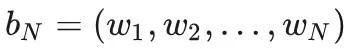
定義 N-gram 熵(Entropy)FN 如下。
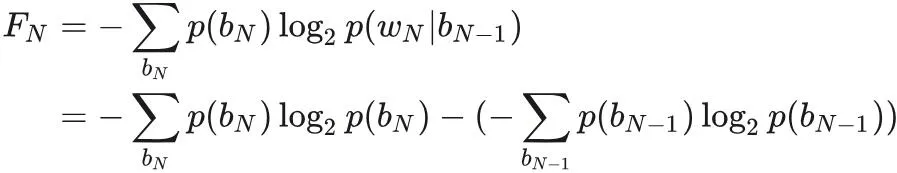
當已知前 N - 1 個字母時,我們可以統計計算出下一個字母的熵。隨著 N 的增加,熵接近 H,此即英語的熵。以下是香農論文中計算出的值。FN 是當已知前 N - 1 個字母時與第 N 個字母相關的熵。計算 FN 統計數據的難度是 O (26^N),因為有那么多 N 個字母的序列。請注意,F0 只是字母集的最大熵,其中每個字母都有相等的概率。

27 個字母的序列,空格也算作一個字母。幾乎總是可以從沒有空格的單詞序列中填充空格。因此空格基本上被視為是多余的,如果考慮空格,會導致計算出的熵值較低。只有在沒有考慮統計數據的情況下,即 F0,添加空格后熵才會更高。這只是增加了另一個可能的符號,就意味著更多的不確定性。
香農建議的另一種策略是計算與英語中每個單詞相關的熵,然后取加權平均值。香農使用近似函數來估計超過 8000 個單詞的熵。他得到的每個單詞的熵值為 11.82 bit,由于平均每個單詞有 4.5 個字母,因此每個字母的熵為 2.62 bit。這在上表中以 Fword 給出。
我們已經討論了如何從熵計算冗余度。當所有符號具有相同的可能性時,冗余度最大,等于 - (log2 (1/26)) = 4.7 bit / 字母。因此,使用公式 1 - H/Hmax,我們可以估算英語的冗余度。香農最初估計這個值為 50%,這意味著英語中大約一半的字母是多余的!
在同一篇文章的后面討論了一種相當巧妙的計算英語熵的方法。它結合了英語的更多特征,例如統計方法無法明確解釋的思路和上下文。
接下來就是如今我們在 NLP 中經常會提起的概念了:假設人類可以根據他們對該語言的先前了解來猜測單詞或短語中的字母。香農的巧妙想法是利用這種自然的冗余度衡量標準…… 人類的思維。
他要求受試者逐個猜測短語中的字母。如果受試者猜對了,那么他 / 她就繼續猜測下一個字母。如果不是,則告訴受試者下一個字母。在一個短語的 129 個字母中,69% 被猜對了。這意味著英語的冗余度大約為 69%。假設我們只重現那些猜錯的字母,即 31%。那么我們可以通過復制從頭開始猜測的受試者來恢復原始句子。受試者顯然可以正確猜出 69% 的符號,并且他 / 她擁有其余的 31%,因此他 / 她可以僅使用大約 31% 的信息重現原始文本。
實際上,受試者需要的信息略多于 31%。他 / 她需要知道他 / 她會猜錯的字母在哪里,因此實際上冗余度可能會少一點。從理論上講,這是一個很好的例子,但實際上并非如此。句子和受試者的抽樣誤差會導致結果嚴重失真。盡管如此,這個例子有助于說明冗余的一個實際例子,并闡明了如何編碼英語。無需創建英語的統計語法來計算其熵,人類天生就具有語法。
統計計算英語的冗余有許多實際應用。ASCII 每個字符保留 8 個二進制數字。然而,考慮到一些計算將英語的熵定為大約 1 位 / 字母,這是非常低效的。這意味著理論上存在一種壓縮方案,其壓縮效果是 ASCII 的 8 倍。現代計算機顯然擁有足夠大的內存,因此這種低效率并不重要,但 Huffman 壓縮和 Lempel-Ziv 壓縮算法在存儲文本時可以節省大量空間。
通常,當人們說英語是冗余的時,他們指的是大量同義詞使我們的詞典變得雜亂。信息論意義上的冗余是衡量字母 / 符號在語言中使用效率的指標。英語是一種冗余語言,這不一定是壞事。我們的語言既可以口語也可以書寫,除了效率之外,還帶來了許多問題。我們希望在嘈雜的房間里也能被人聽懂,我們希望單詞的發音與含義相對應,我們希望能夠輕松地發音。信息率只是英語分析的一小部分。
一個非常有趣的例子可以說明一種語言在統計上能有多好地描述,即英語的 n 階近似,這是香農最著名的論文《A mathematical theory of communication》里所提到的。如果一只猴子知道英語中字母的 n-gram 頻率(其中 n 很大),它能寫出可信的英語文本嗎?此外,這只猴子「懂」英語嗎?如果 N-gram 猴子在一扇門后面,而人類在另一扇門后面,第三方觀察者能分辨出哪個是猴子嗎?這個問題讓人想起了人工智能的圖靈測試,它沒有簡單的答案。
但如今的大模型原理,正是通過學習大量的文本數據,來預測下一個詞或下一段話的可能性,從而使計算機能夠更好地「理解」和生成人類語言。

AI 理解了嗎?不好說。但是能猜對嗎?看看如今的 ChatGPT,人們心中都已經有了答案。
這也不禁令人感嘆,香農真的領先于他的時代。