4月30日，KAN橫空出世，很多人預言這會敲響MLP的喪鐘。

沒想到，子彈還沒飛4個月，核心團隊又推出了KAN 2.0，瞄準AI+Science領域，進一步挖掘了KAN的潛力。

這篇論文更雄心勃勃的地方在于，作者希望通過一種框架來彌合AI世界的連接主義（connectionism）和科學世界的符號主義（symbolism）之間的不相容性。

通過提出pykan等工具，作者還展現了KAN發現各種物理定律的能力，包括守恒量、拉格朗日量、隱藏對稱性和本構方程等等。

論文地址：https://arxiv.org/abs/2408.10205

這次KAN 2.0依舊出自初代架構原班人馬之手。

深度學習變天了，MLP成過去式？

我們先簡要回顧一下，今年4月首次提出的KAN究竟在哪些方面改進了MLP。

MLP（multi-layer perceptron）又被稱為全連接神經網絡，是當今幾乎所有深度學習模型的基礎構建塊，它的出世甚至可以追溯到第一波人工智能浪潮方興未艾的1958年。

論文地址：https://www.ling.upenn.edu/courses/cogs501/Rosenblatt1958.pdf

KAN的論文中都表示，MLP的重要性怎么強調都不為過，因為這是神經網絡中用于逼近非線性函數的默認模型，其對函數表達能力的底層邏輯由「通用逼近定理」保證。

Transformer和其他架構中常見的FFN本質上就是一個MLP。但由于網絡稠密、參數量大，MLP往往占據了模型中幾乎所有的非編碼層參數。

而且相比注意力層，在沒有后期分析工具時，MLP中的大量參數也缺乏可解釋性。

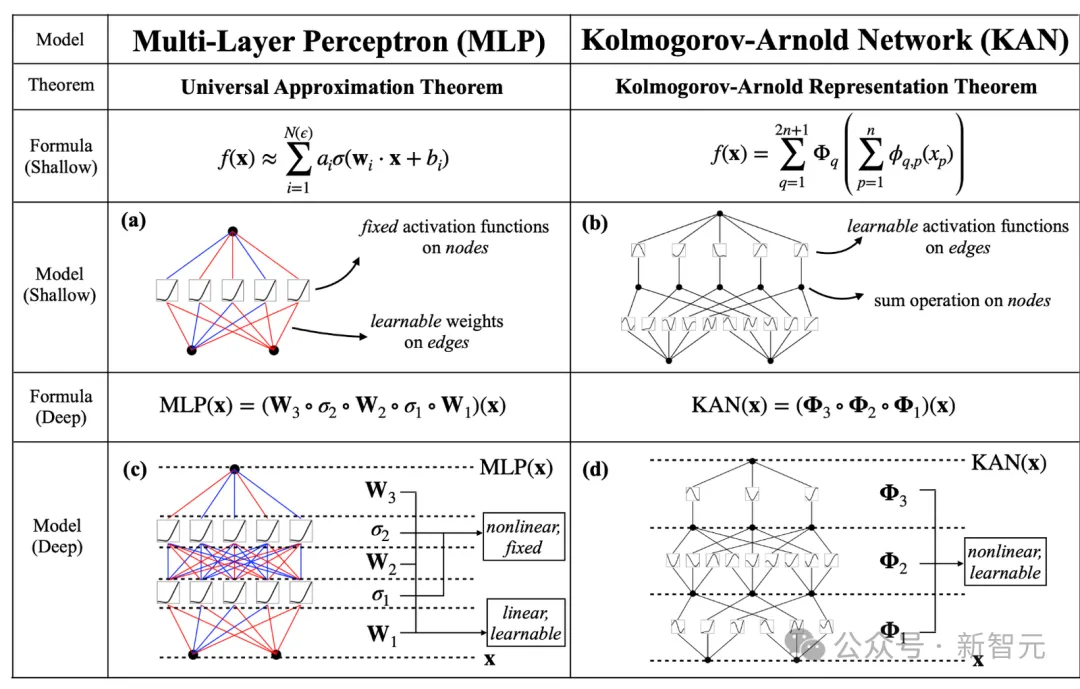
受到Kolmogorov-Arnold表示定理的啟發，KAN打破了對通用逼近定理的遵循。

雖然底層邏輯變了，但是他們做出的修改相當簡潔且直觀：

- 將激活函數放在網絡邊緣而非節點處

- 給激活函數賦予可學習參數，而非固定的函數

KAN中沒有任何線性權重，網絡中的每個權重都變成了B-spline型單變量函數的可學習參數。

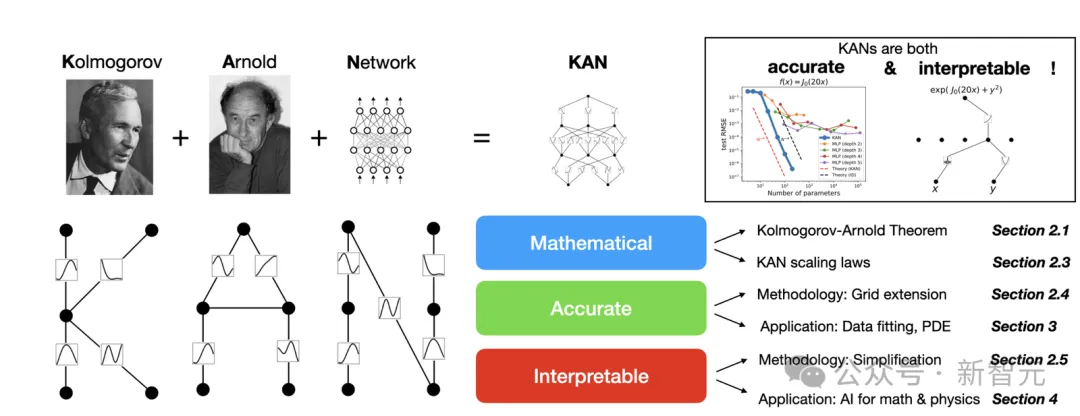
這種看似簡單的改變讓KAN獲得了擬合準確性和可解釋性方面的優勢。今年4月的第一篇論文中，作者們就發現KAN在數學和物理定律方面的潛力。

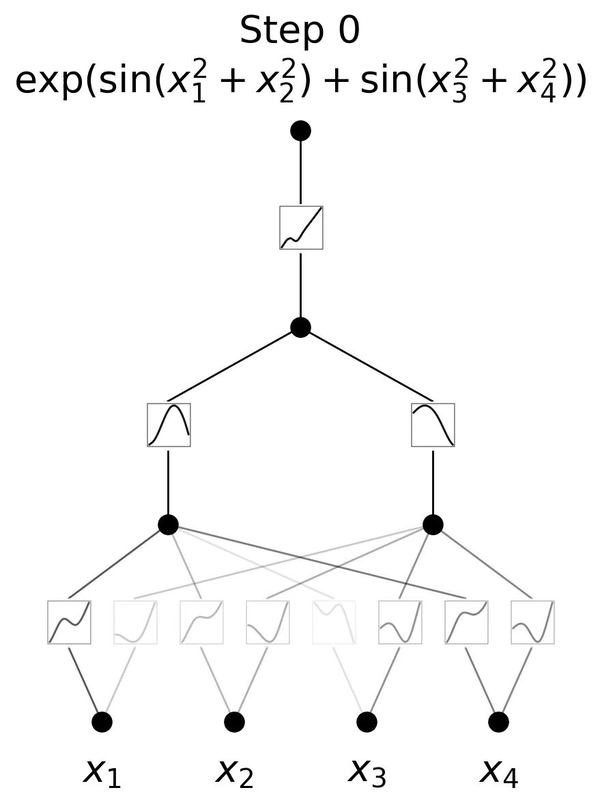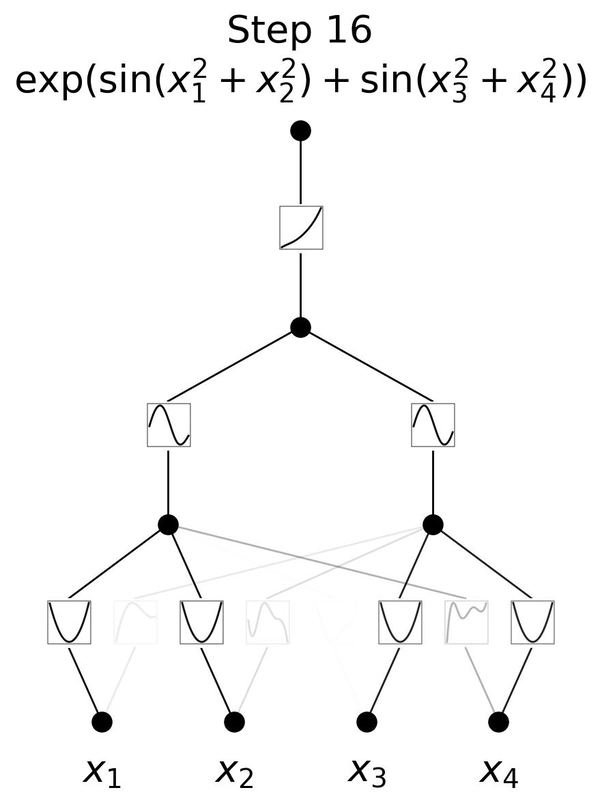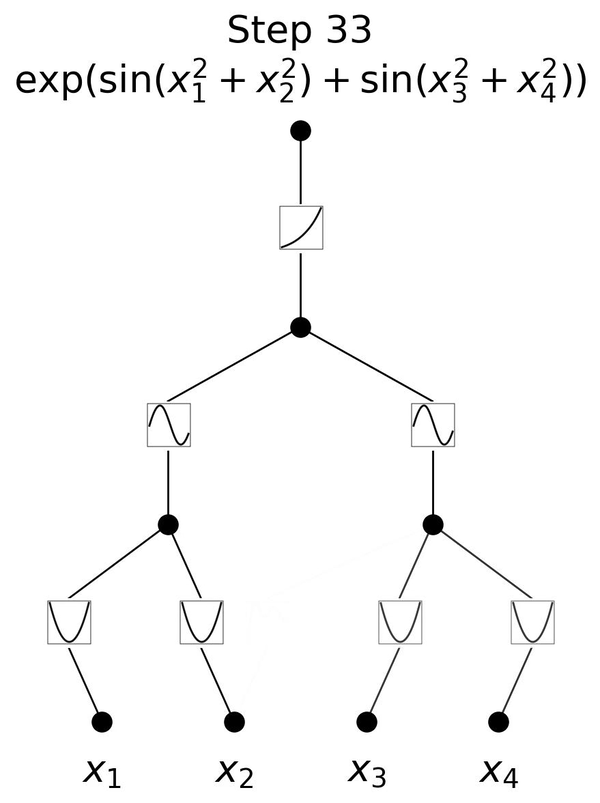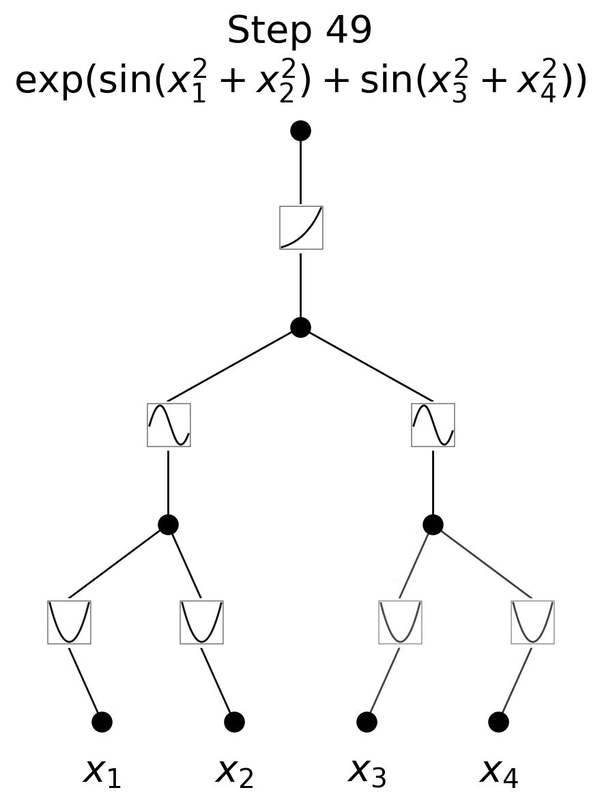
下面這個動圖展示了簡單的3層KAN網絡擬合一個復雜函數的訓練過程，相當簡潔清楚。

此外，KAN也能從根本上很好地解決MLP中普遍存在的「災難性遺忘」問題。

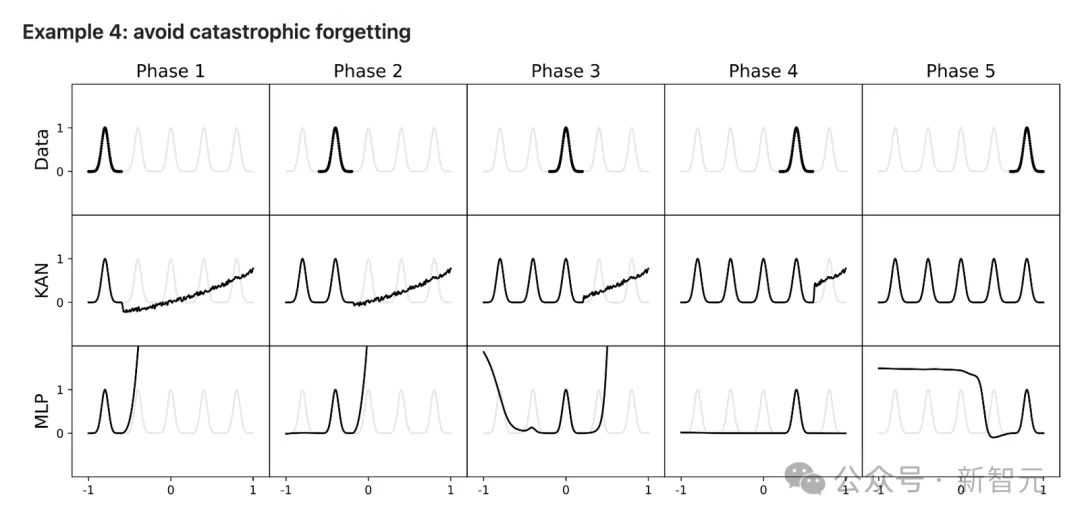
以上這些優勢，都奠定了KAN作為「科學家合作助手」的基本能力。

KAN2.0問世，一統AI+科學

雖然第一版的KAN網絡本身有很多適合科學研究的優點，但深度學習和物理、化學、生物學領域依舊有完全不同的「語言」，這構成了AI4Science最大的障礙之一。

因此擴展后的KAN 2.0的終極目標只有一個——使KAN能輕松應用于「好奇心驅動的科學」。研究人員既能將輔助變量、模塊化結構、符號公式等科學知識集成到KAN中，也能從KAN的可解釋性分析中得到觀察和見解。

所謂「好奇心驅動的科學」，根據論文的解釋，是過程更具有探索性、提供更基礎層面新發現和新知識的研究，比如天體運動背后的物理原理，而非AlphaFold這類應用驅動的科學研究。

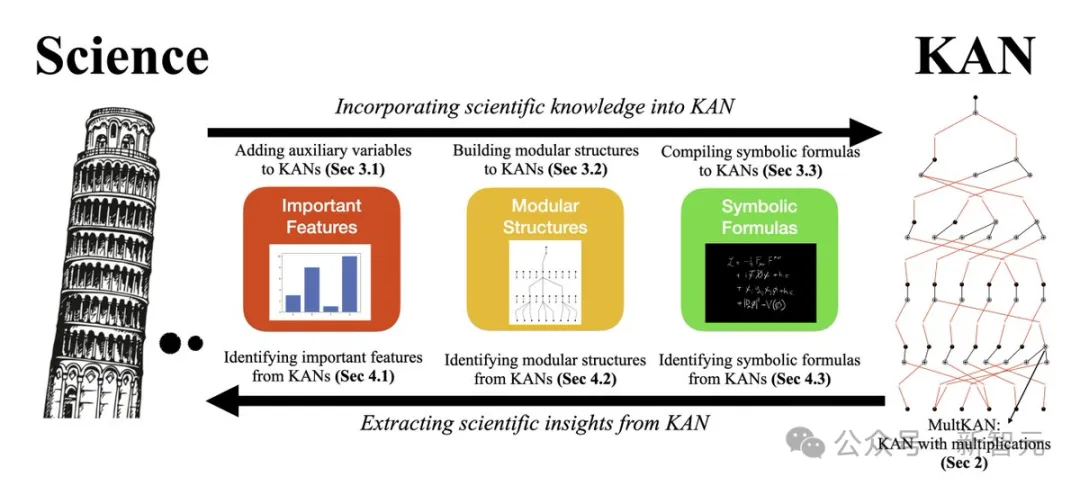
科學與KAN的協同

具體來說，科學解釋有不同的層次，從最簡單粗略到最精細、最難發現、最具因果性，可以有如下幾個分類：

- 重要特征：例如，y完全由x₁和x₂決定，其他因素并不重要；即存在一個函數f使得y=f(x₁, x₂)

- 模塊化結構：例如，存在函數g和h是的y=g(x₁)+h(x₂)

- 符號公式：例如，y=sin(x₁)+exp(x₂)

MultKAN

在原始KAN網絡的基礎上，這篇最新的論文引入了一種稱為MultKAN的新模型，其核心改進是引入額外的乘法層進行增強。

KAN所依據的Kolmogorov-Arnold表示定理提出，任何連續高維函數都可以分解為單變量連續函數和加法的有限組合：

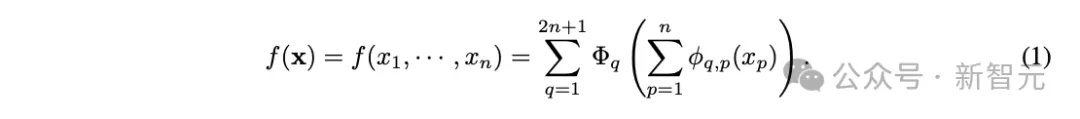
這意味著加法是唯一真正的多元運算，，而其他多元運算（包括乘法）都可以表示為與單變量函數組合的加法。因此，原來的KAN中僅包含加法運算。

然而，考慮到乘法在科學和日常生活中的普遍存在，MultKAN中明確包含乘法，能更清楚地揭示數據中的乘法結構，以期增強可解釋性和表達能力。

如圖2所示，MultKAN和KAN相似，都包含標準KAN層，但區別在于插入了乘法節點，對輸入的子節點進行乘法運算后再進行恒等變換，用Python代碼可表示為：

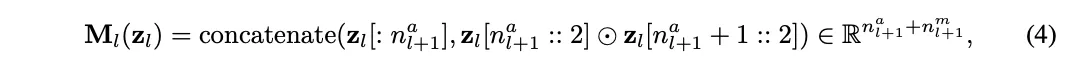
其中⊙表示逐元素乘法。

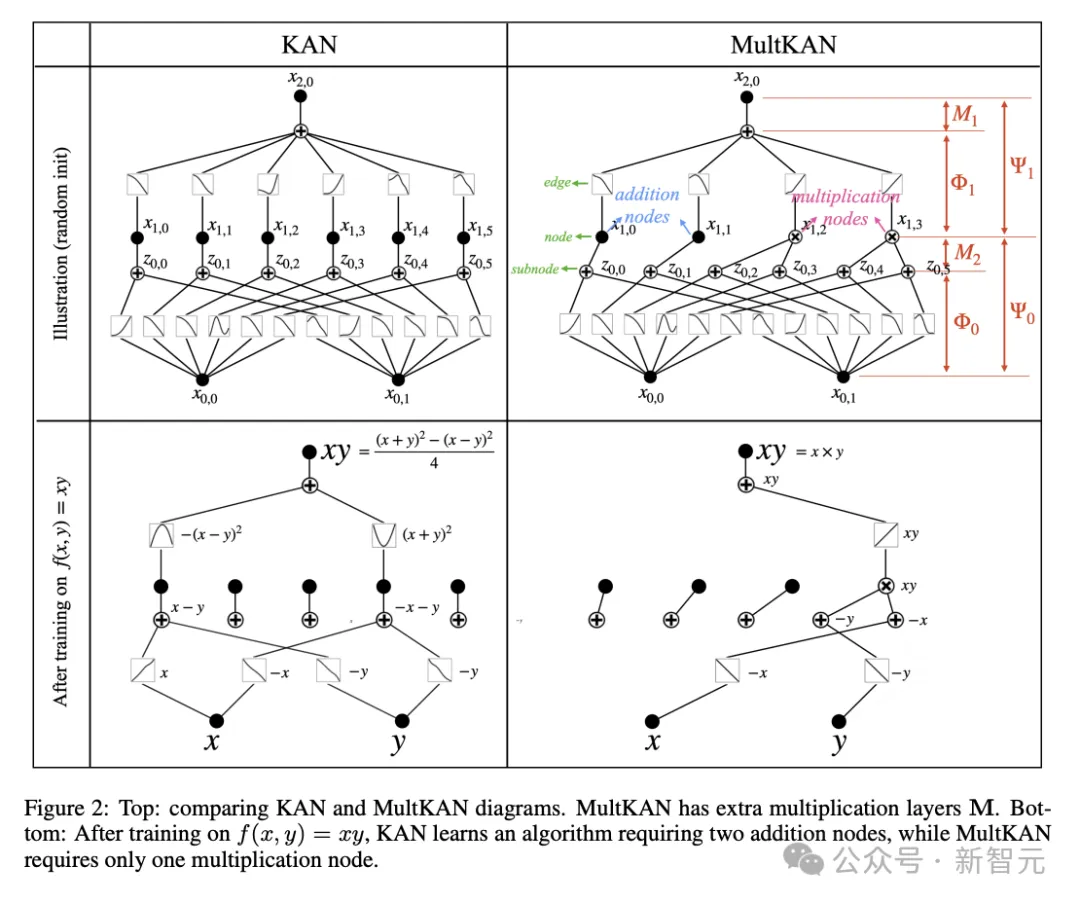
根據上圖，整個MultKAN網絡進行的運算就可以寫作：

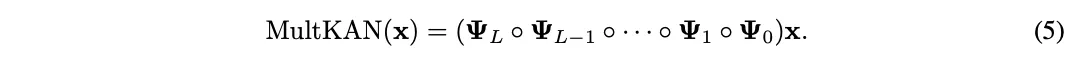
其中，??_L≡??_L°??_L。

經過擴展后，論文將KAN和MultKAN視為同義詞，即默認情況下的KAN都將允許乘法層的存在，除非有特殊說明。

GitHub倉庫中的KAN代碼已經更新，可以通過pip快捷命令直接安裝使用。

倉庫地址：https://github.com/KindXiaoming/pykan

Science to KAN

在科學領域，領域知識至關重要，讓我們可以在數據稀少或不存在的情況下，也能有效工作。

因此，對KAN采用基于物理的方法會很有幫助：將可用的歸納偏置整合到KAN中，同時保持其從數據中發現新物理規律的靈活性。

文中作者探討了三種可以整合到KAN中的歸納偏置，從最粗略（最簡單/相關性）到最精細（最困難/因果關系）：重要特征、模塊化結構和符號公式。

在KANs中添加重要特征

在回歸問題中，目標是找到一個函數f，使得y=f(x₁, x₂, ···, x_n)。假設我們希望引入一個輔助輸入變量a=a(x₁, x₂, ..., x_n)，將函數轉化為y=f(x₁, ···, x_n, x_a)。

盡管輔助變量a不增加新的信息，但它可以提高神經網絡的表達能力。這是因為網絡無需消耗資源來計算輔助變量。此外，計算可能變得更簡單，從而提升可解釋性。

這里，用戶可以使用augment_input方法向輸入添加輔助特征：

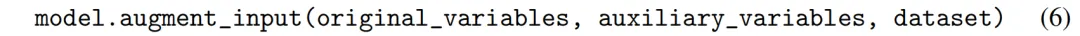
圖3顯示了包含輔助變量和不包含這些輔助變量的KAN：（a）由符號公式編譯而成的KAN，需要5條連接邊；（b）（c）包含輔助變量的KAN，僅需2或3條連接邊，損失分別為10??和10??。

為KAN構建模塊化結構

模塊化在自然界中非常普遍：比如，人類大腦皮層被劃分為幾個功能不同的模塊，每個模塊負責特定任務，如感知或決策。模塊化簡化了對神經網絡的理解，因為它允許我們整體解釋神經元群集，而不是單獨分析每個神經元。

結構模塊化的特點是連接群集，其中特征是群集內的連接遠強于群集間的連接。為此，作者引入了module方法：保留群集內的連接，同時去除群集間的連接。

模塊由用戶來指定，語法是：

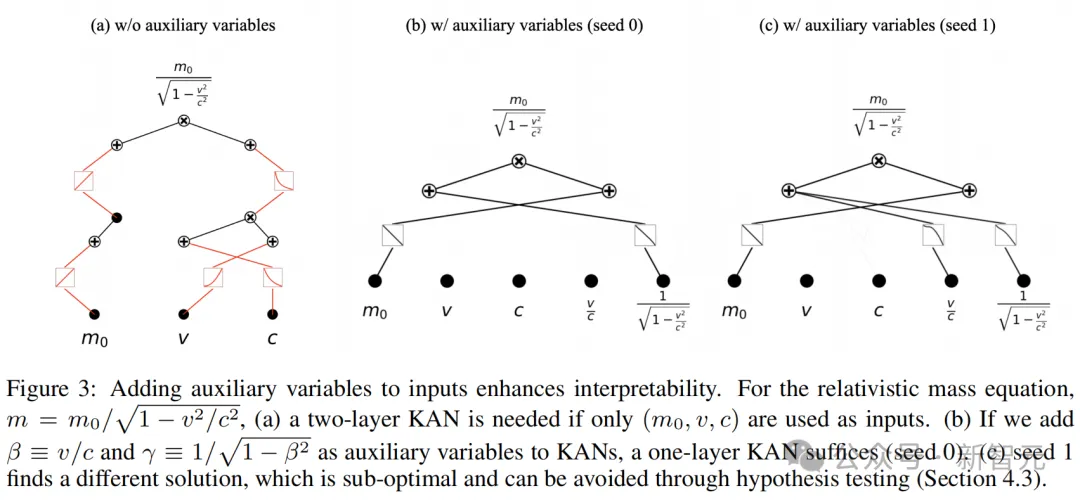
具體而言，模塊化有兩種類型：可分性和對稱性。

可分性：如果說一個函數是可分的，那么它就可以表示為非重疊變量組的函數的和或積。

廣義對稱性：如果f(x₁, x₂, x₃, ···)=g(h(x₁, x₂), x₃, ···)，則這個函數在變量(x₁, x₂)上是對稱的。因為只要h(x₁, x₂)保持不變，即使x₁和x₂發生變化，f的值仍然保持不變。

將符號公式編譯成KAN

為了結合「符號方程」和「神經網絡」這兩種方法的優勢，作者提出了一個兩步程序：（1）將符號方程編譯成KAN，（2）使用數據微調這些KAN。

其中，第一步可以將已知的領域知識嵌入到KAN中，而第二步則專注于從數據中學習新的「物理」知識。

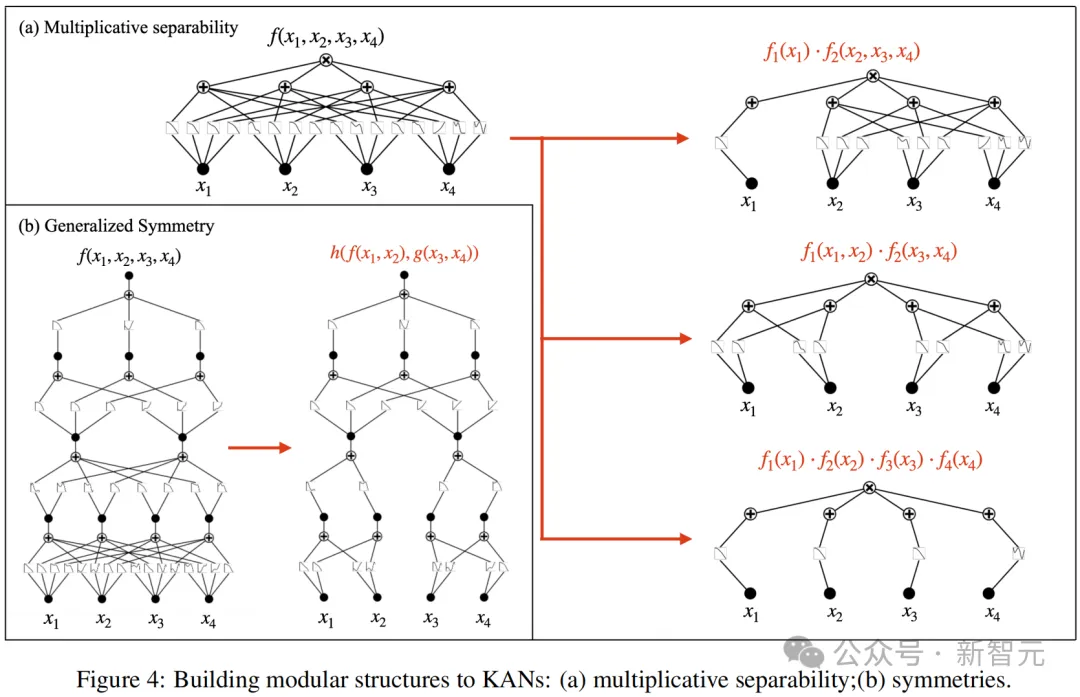
具體來說，作者首先提出了用于將符號公式編譯成KAN的kanpiler（KAN編譯器）。過程如圖5a所示：

1. 將符號公式解析為樹結構，其中節點表示表達式，邊表示操作/函數；

2. 然后修改該樹以與KAN圖結構對齊。修改包括通過虛擬邊將所有葉節點移動到輸入層，并添加虛擬子節點/節點以匹配KAN架構。這些虛擬邊/節點/子節點僅執行恒等變換；

3. 在第一層中組合變量，有效地將樹轉換為圖。

然而，通過寬度/深度擴展來增加表達能力kanpiler生成的KAN網絡是緊湊的，沒有冗余邊，這可能限制其表達能力并阻礙進一步的微調。

為了解決這個問題，作者又提出了expand_width和expand_depth方法來擴展網絡，使其變得更寬和更深，如圖5c所示。

KAN to Science

這一節同樣關注提取知識的三個層次，從最基本到最復雜：重要特征，模塊化結構和符號公式。

識別重要特征

給定一個回歸模型f，有y≈f?(x₁,x₂,…,x_n) ，我們的目標是為輸入變量分配重要性分數。

論文提出，之前所使用的L1范數（圖6a）只考慮到了局部信息，因此得出的結果可能存在問題。

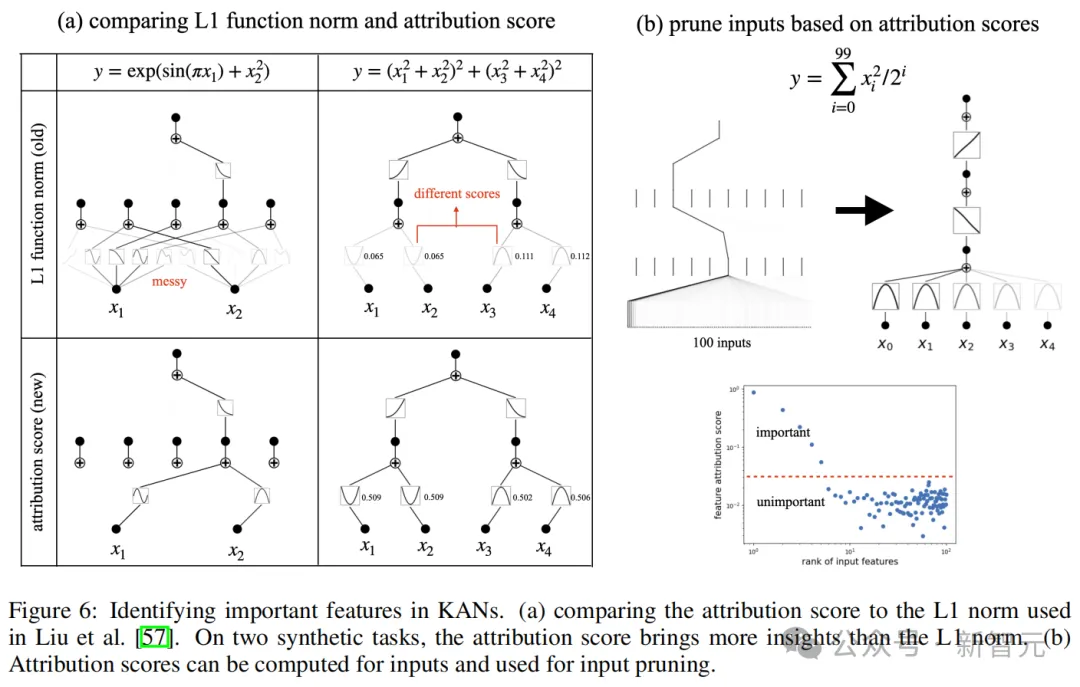
依據KAN網絡，作者提出了一種更有效的歸因分數，能比L1范數更好反映變量的重要性，還可以根據這種歸因分數對網絡進行剪枝。

 識別模塊化結構

歸因分數可以告訴我們哪些邊或節點更有價值，但它沒有揭示模塊化結構，即重要的邊和節點如何連接。

神經網絡中的模塊化結構可以分為兩種：解剖模塊化（anatomical modularity）和功能模塊化（functional modularity）。

解剖模塊化是指，空間上彼此靠近的神經元相比距離較遠的神經元具有更強的連接趨勢。論文采用了之前研究提出的「神經元交換」方法，在代碼中被稱為auto_swap，可以在保留網絡功能的同時縮短連接，有助于識別模塊。

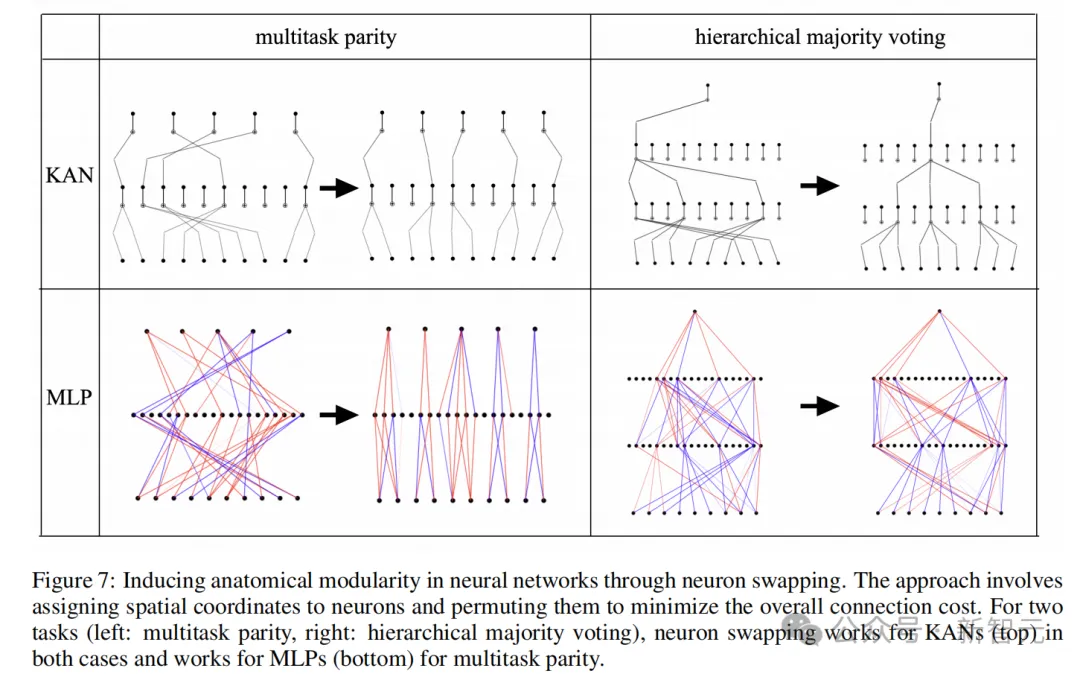
圖7展示了兩個成功識別模塊的auto_swap任務：多任務匹配和分層多數投票。其中，KAN的模塊結構相比MLP更加簡單且富有組織性。

但無論auto_swap結構如何，網絡全局的模塊化結構仍和整體功能仍不清楚，這就需要用到功能模塊化分析，通過輸入和輸出的前向和后向傳遞來收集有關信息。

圖8定義了三種類型的功能模塊化：可分性、一般可分性和一般對稱性。

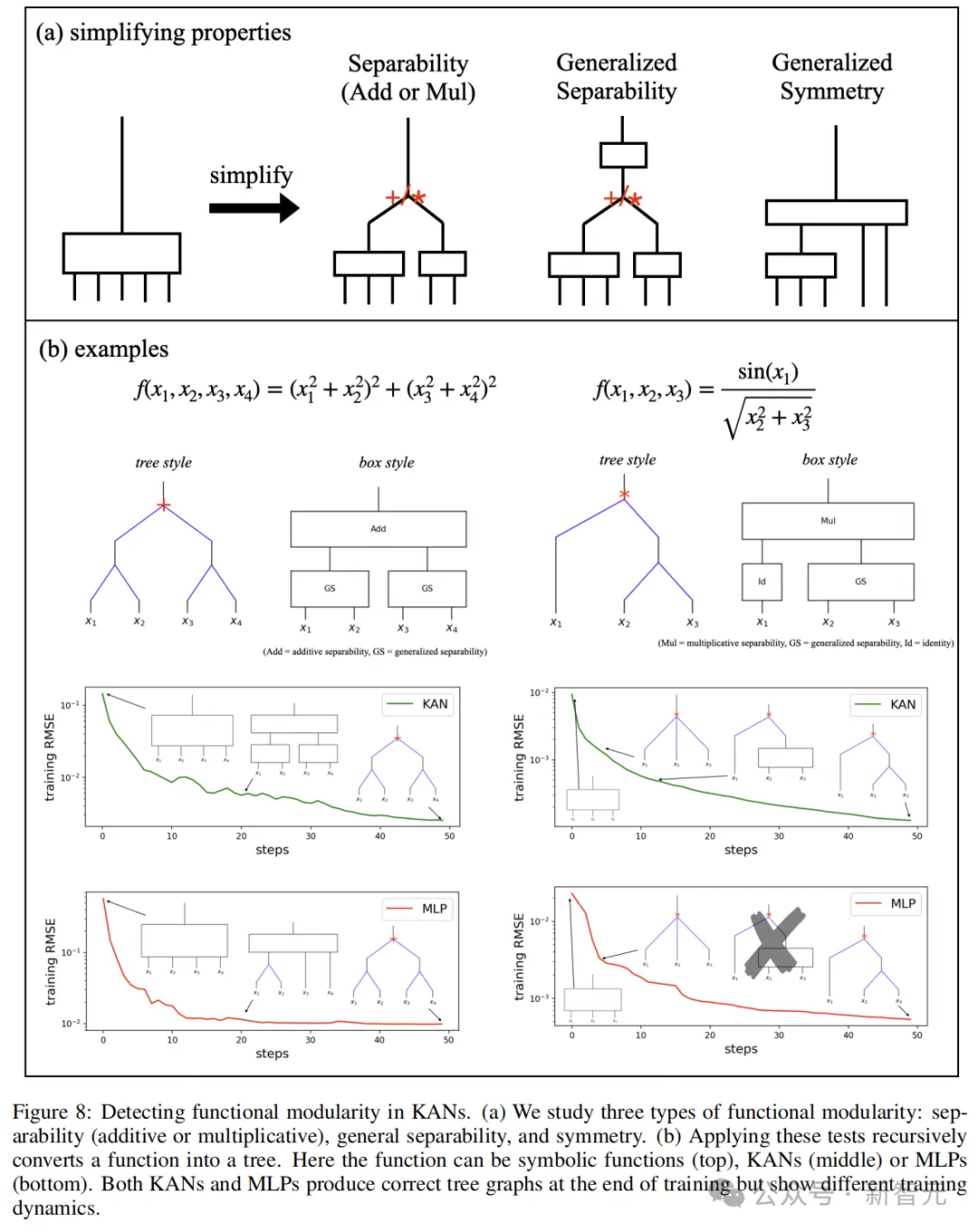
 識別符號公式

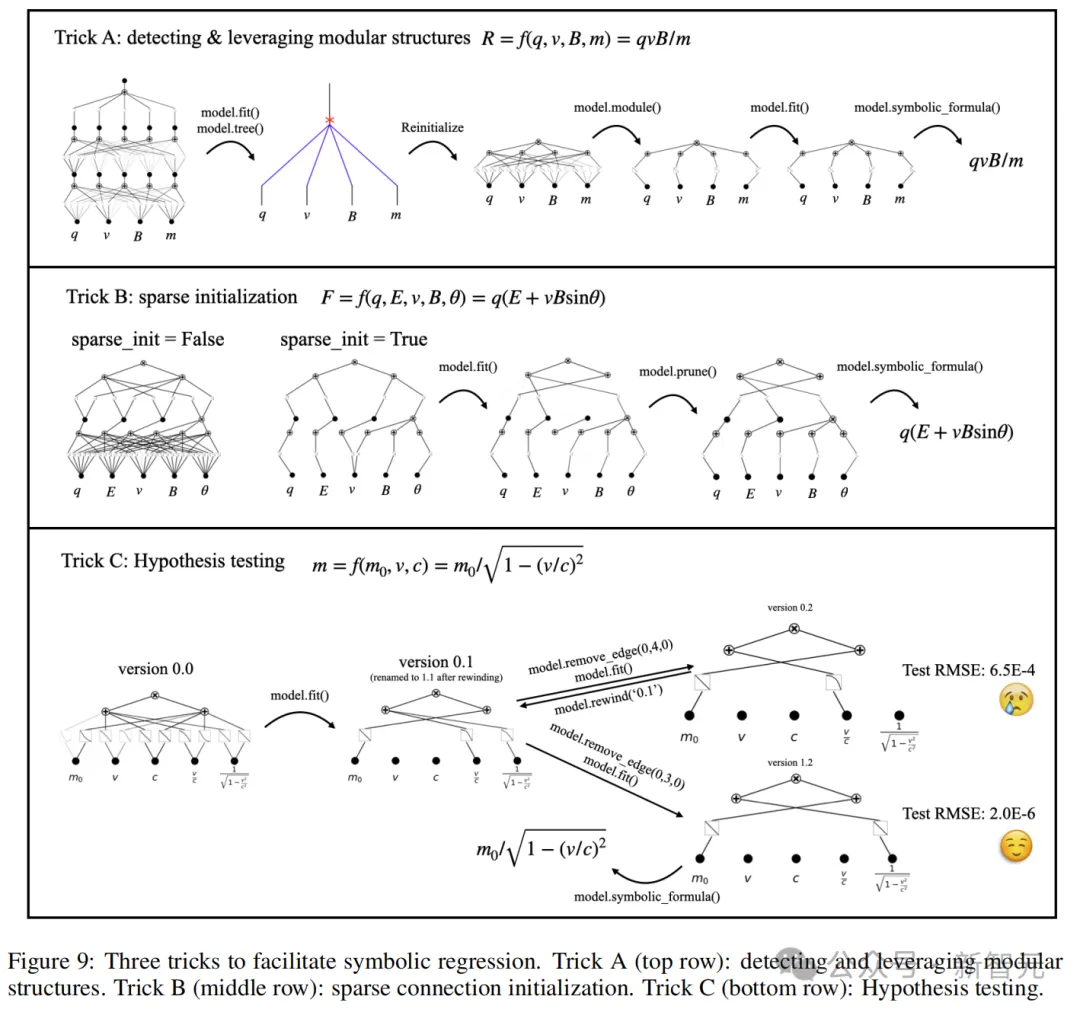
符號公式信息量最大，因為可以直接、清楚地揭示函數中重要的特征和模塊結構。圖9展示了與KAN進行交互協作進行符號回歸的3個技巧：

1.發現并利用模塊化結構

2.稀疏初始化

3.假設檢驗

用KAN助力物理學研究

除了進行原理層面的說明，論文還講解了多個具體案例，如何將KAN融入到現實的科學研究中，比如發現新的物理概念和定律。

論文給出的案例包括守恒量、拉格朗日量、隱藏對稱性和本構方程等。這里我們以最簡單的守恒量發現為例，看看KAN是如何工作的。

守恒量即時間變化過程中保持恒定的物理量，比如能量守恒定律告訴我們，孤立系統的總能量保持不變。

傳統上，科學家如果不借助計算工具，僅靠紙筆推導守恒量可能非常耗時，并且需要廣泛的領域知識。但機器學習方法可以將守恒量參數化，轉化為求解微分方程的問題。

此處所用的方法基本類似于作者Ziming Liu等人2022年發表的論文，但將其中的MLP網絡換成了KAN。

論文地址：https://pubmed.ncbi.nlm.nih.gov/36397460/

比如使用KAN可以發現二維諧振子(x, y, p_x, p_y)中具有3個守恒量：x軸方向的能量H₁、y軸方向的能量H₂和角動量H₃。

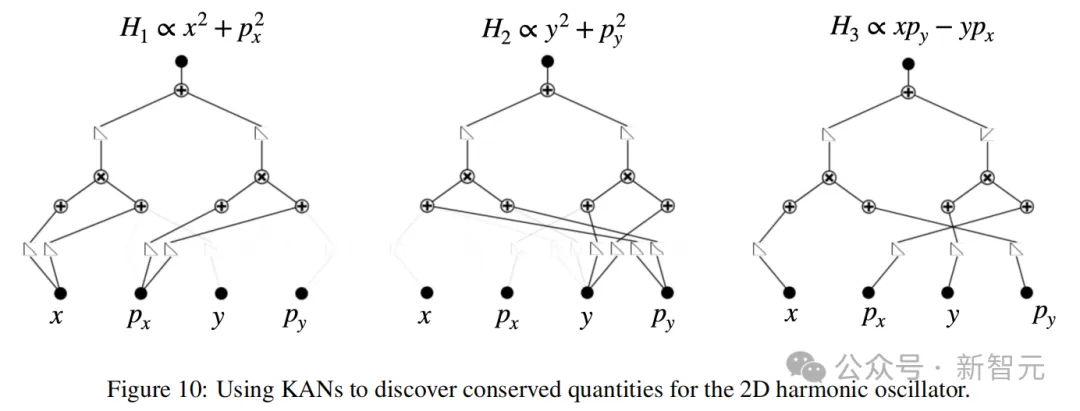
關于KAN的其他應用，論文也描述了如何從實驗數據中推斷出拉格朗日量（圖11）。

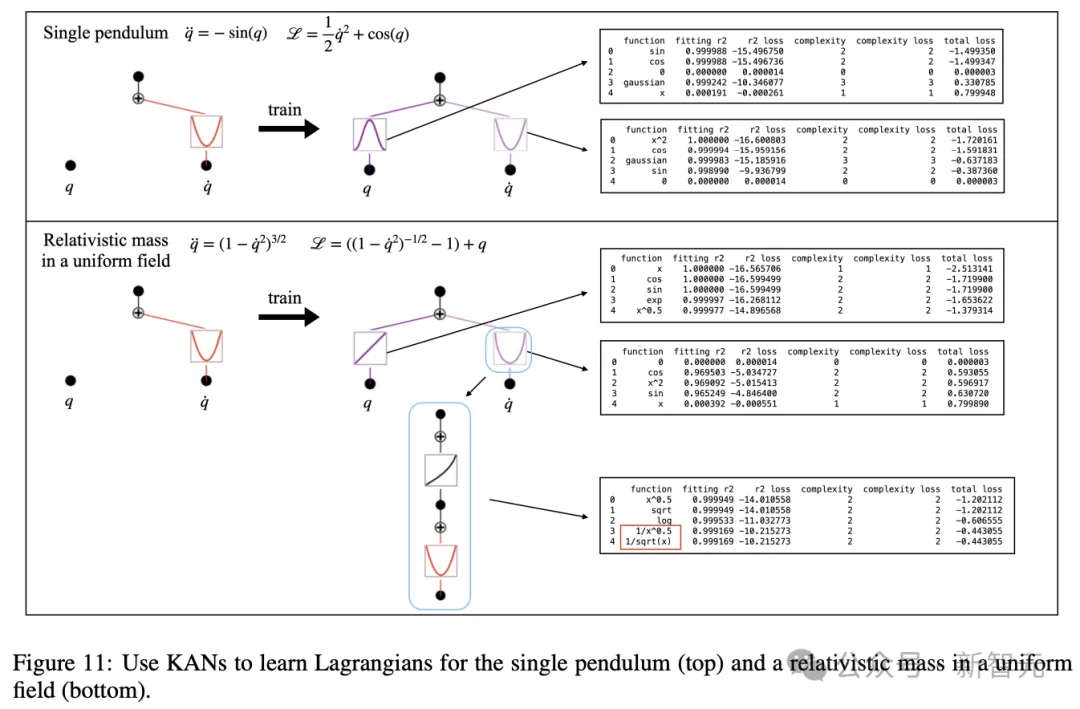
或者，發現Schwarzschild黑洞中的隱藏對稱性（圖12）。

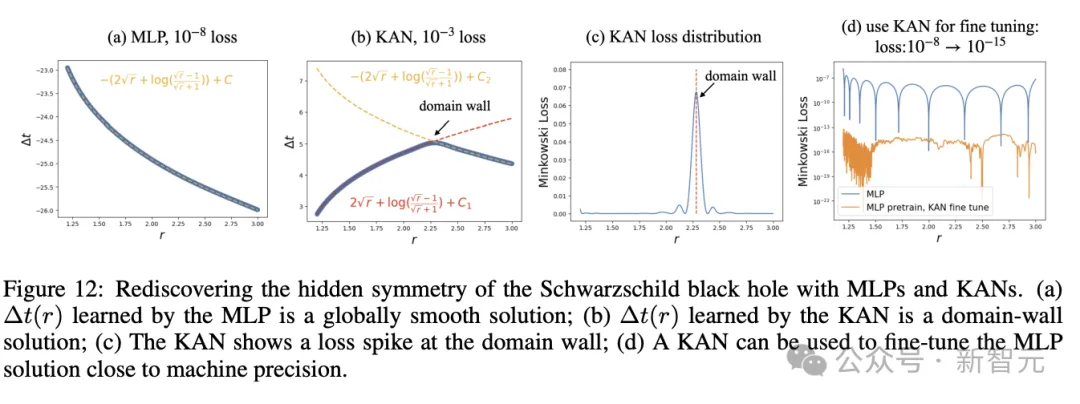
還有數據驅動的本構定律發現（圖13）。本構定律通過模擬材料對外力或變形的響應，定義材料的行為和屬性，比如描述彈簧的胡克定律。

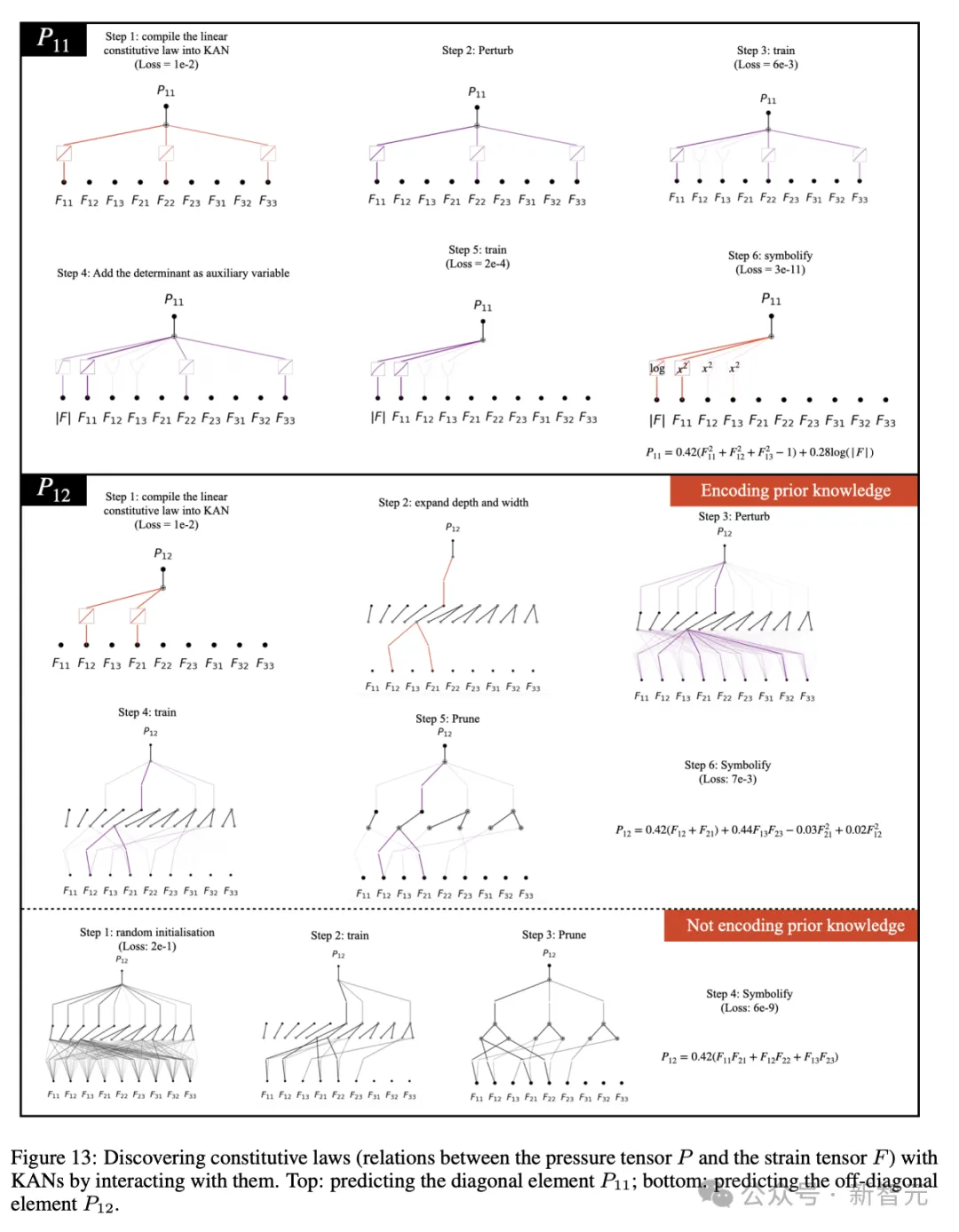
作者介紹

Ziming Liu（劉子鳴）

Ziming Liu目前是MIT和IAIFI的三年級博士生，由Max Tegmark教授指導。他是兩篇KAN論文的第一作者，可以說是這個架構背后最主要的貢獻者。

他的研究興趣主要集中在AI與物理學（以及其他科學領域）的交叉區域：

1. Physics of AI：從物理學原理來理解AI，目標是讓「AI像物理學一樣簡單」；

2. Physics for AI：受物理學啟發的AI，目標是讓「AI像物理學一樣自然」；

3. AI for physics：利用AI增強物理學研究，目標是讓「讓AI像物理學家一樣強大」。

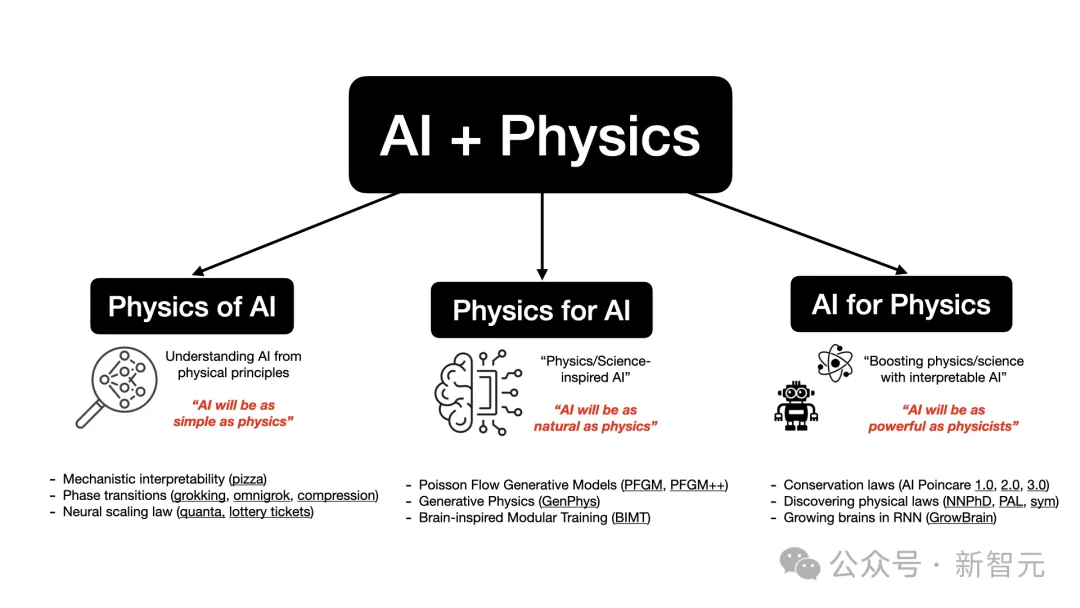
為了實現利用AI和物理學共建更美好世界的最終目標，Ziming Liu對包括發現物理定律、受物理啟發的生成模型、機器學習理論、機械解釋性等在內的多個主題都有深厚的興趣。

并且，與凝聚態、高能物理、量子計算等領域的物理學家以及計算機科學家、生物學家、神經科學家和氣候科學家等建立了緊密合作關系。

他多次在頂尖的物理期刊和AI會議上發表論文，并擔任IEEE、Physical Review、NeurIPS、ICLR等的審稿人。同時，還共同組織了NeurIPS 2021和ICML 2022的AI4Science workshop。

在攻讀博士學位之前，他在北京大學獲得了物理學學士學位，并曾在微軟亞洲研究院實習。

Pingchuan Ma（馬平川）

Pingchuan Ma目前是MIT CSAIL實驗室的博士生，由Wojciech Matusik教授指導。

他的研究方向涵蓋了「基于物理的智能」的整個流程：

1. 重建高效逼真的物理環境

2. 基于這些環境生成AI 智能體

3. 在物理世界中實現這些智能體

此前，他在南開大學獲得軟件工程專業學士學位，并在麻省理工學院獲得計算機科學碩士學位。

同時，他還在IBM、字節、商湯、港大等知名機構從事過研究工作，有著豐富的經驗。

Yixuan Wang

Yixuan Wang目前是加州理工學院，應用及計算數學專業的博士生。

他的研究方向十分廣泛，包括數值分析、偏微分方程、應用概率，以及AI for Science。

此前，他在北京大學獲得數學學士學位。

Wojciech Matusik

Wojciech Matusik是麻省理工學院計算機科學與人工智能實驗室（MIT CSAIL）的電氣工程與計算機科學教授，也是計算機圖形學小組的成員，負責帶領計算設計與制造團隊。

他的研究興趣包括計算機圖形學、計算設計與制造、計算機視覺、機器人學和人機交互。

他于2003年在MIT獲得計算機圖形學博士學位，2001年在MIT獲得電氣工程與計算機科學碩士學位，1997年在加州大學伯克利分校獲得電氣工程與計算機科學學士學位。

并他曾在三菱電機研究實驗室、Adobe和迪士尼蘇黎世研究所工作。

2004年，他被「麻省理工科技評論」評為全球100位頂尖青年創新者之一。2009年，獲得了ACM Siggraph的杰出新研究者獎。2012年，獲得了DARPA青年教師獎，并被評為斯隆研究學者。2014年，獲得了Ruth和Joel Spira卓越教學獎。

Max Tegmark

Max Tegmark被大家親切地稱為「瘋狂的麥克斯」（Mad Max）。

憑借著自己創新的思維和對冒險的熱情，他的科研興趣涵蓋從精確宇宙學到探索現實的終極本質。

比如，結合理論與新的測量技術，精確限定宇宙學模型及其參數。在他作為物理學研究者的前25年里，這種研究方向使他主要關注宇宙學和量子信息學。

雖然他仍與HERA合作研究宇宙學，但目前他的主要研究方向是智能的物理學，即運用物理方法深入探索生物智能和AI。

作為麻省理工學院的物理學教授，他發表了超過兩百篇技術論文，并多次在科學紀錄片中出現。他在SDSS項目中關于星系聚類的研究，贏得了《科學》雜志「2003年度突破」的第一名。

在此之前，Tegmark于1989年在斯德哥爾摩經濟學院獲得了經濟學學士學位，1990年在皇家理工學院獲得物理學學士學位。

畢業后，他便前往加州大學伯克利分校繼續深造，先后獲得物理學碩士和博士學位。

在美國西海岸生活四年后，他回到了歐洲，出任馬克斯·普朗克物理研究所的助理研究員。

1996年，他作為Hubble Fellow以及普林斯頓高級研究院的研究員，再次來到美國。

幾年后，他獲得賓夕法尼亞大學的助理教授職位，并于2003年獲得終身教職。

2004年，他來到MIT并定居在查爾斯河畔的劍橋。