特征重要性是解釋機器學習模型最常用的工具。這導致我們常常認為特征重要性等同于特征好壞。

事實并非如此。

當一個特征很重要時，它僅僅意味著模型發現它在訓練集中很有用。但是，這并不能說明該特征在新數據上的泛化能力！。

為了說明這一點，我們需要區分兩個概念：

• 預測貢獻：變量在模型預測中的權重。這是由模型在訓練集中發現的模式決定的。這相當于特征重要性。
• 錯誤貢獻：模型在暫存數據集上的錯誤中，變量所占的權重。這可以更好地反映特征在新數據上的表現。

在本文中，我將解釋在分類模型中計算這兩個量背后的邏輯。我還將舉例說明在特征選擇中使用 "誤差貢獻 "比使用 "預測貢獻" 會得到更好的結果。

假設我們有一個分類問題，想要預測一個人的收入是低于還是高于 10k。還假設我們已經有了模型的預測結果：

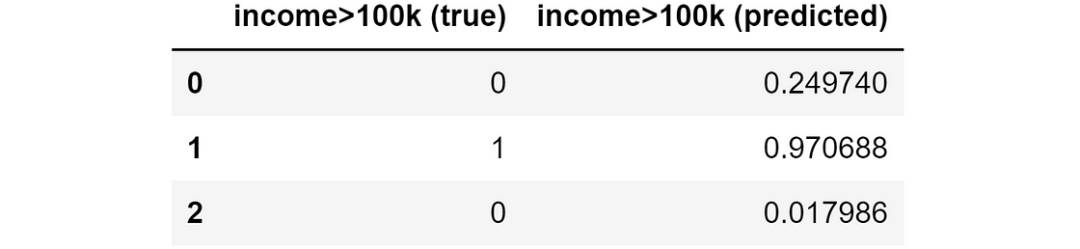實際值和模型預測

預測和誤差貢獻的計算主要基于模型對每個個體的誤差以及每個個體的 SHAP 值。因此，我們必須花一點時間來討論兩個相關問題：

• 分類模型應該使用哪種 "誤差"？
• 我們應該如何管理分類模型中的 SHAP 值？

我將在接下來的兩段中討論這些問題。

在分類模型中使用哪種 "誤差"？

我們的主要目標是計算模型中每個特征的誤差貢獻（Error Contribution）。因此，最重要的問題是：如何定義分類模型中的 "誤差"？

請注意，我們需要一個可以在個體水平上計算的誤差，然后將其匯總到整個樣本中，得到一個 "平均誤差"（回歸模型的絕對誤差請看??顛覆認知！這個特征很重要，但不是個好特征！）。

分類模型最常用的損失函數是對數損失（又名交叉熵）。它是否適合我們。

下面是對數損失的數學公式：

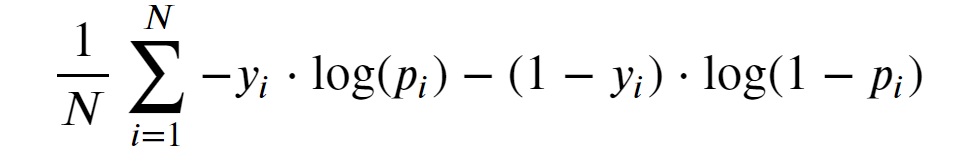圖片

對數損失似乎是最佳選擇，因為

• 公式的外部部分只是一個簡單的平均值；
• "損失"，顧名思義意思是越小越好（就像 "誤差"）。

試著理解一下，為什么我們可以稱它為 "誤差"。為了簡單起見，把注意力集中在和里面的數量上：

圖片

這是單個個體對全局對數損失的貢獻，因此我們可以稱之為 "個體對數損失"。

這個公式看起來仍然很嚇人，但如果我們考慮到，在二元分類問題中，y只能是 0 或 1，我們就可以得到一個更簡單的版本：

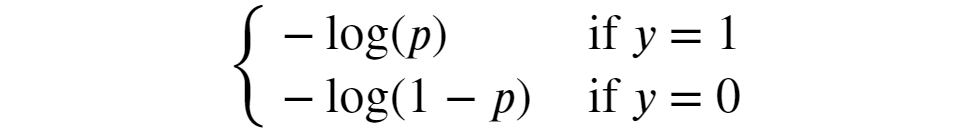圖片

一圖勝千言，現在就很容易理解對數損失背后的主要思想了。

圖片

預測概率與真實值（無論是 0 還是 1）相差越遠，損失就越大。此外，如果預測值與真實值相差很遠（例如，p=.2，y=1 或 p=.8，y=0），那么損失就會比比例損失更嚴重。現在我們應該更清楚為什么對數損失實際上是一種誤差了。

我們準備將單個對數損失公式轉化為一個 Python 函數。

為了避免處理無限值（當 y_pred 恰好為 0 或 1 時會出現這種情況），我們將使用一個小技巧：如果 y_pred 與 0 或 1 的距離小于 ε，我們將其分別設置為 ε 或 1-ε。對于 ε，我們將使用 1^-15（這也是 Scikit-learn 使用的默認值）。

def individual_log_loss(y_true, y_pred, eps=1e-15):
  """Compute log-loss for each individual of the sample."""
  
  y_pred = np.clip(y_pred, eps, 1 - eps)
  return - y_true * np.log(y_pred) - (1 - y_true) * np.log(1 - y_pred)

我們可以使用該函數計算數據集中每一行的單個對數損失：

目標變量、模型預測以及由此產生的個體對數損失

可以看出，個體 1 和個體 2 的對數損失（或誤差）非常小，因為預測值都非常接近實際觀測值，而個體 0 的對數損失較高。

如何管理分類模型中的 SHAP 值？

最流行的模型是基于樹的模型，如 XGBoost、LightGBM 和 Catboost。在數據集上獲取基于樹的分類器的 SHAP 值非常簡單：

from shap import TreeExplainer

shap_explainer = TreeExplainer(model)
shap_values = shap_explainer.shap_values(X)

# 可以定義一個函數來獲取
def get_preds_shaps(df, features, target, ix_trn):
  """Get predictions (predicted probabilities) and SHAP values for a dataset."""
    
  model = LGBMClassifier().fit(df.loc[ix_trn, features], df.loc[ix_trn, target])
  preds = pd.Series(model.predict_proba(df[features])[:,1], index=df.index)
  shap_explainer = TreeExplainer(model)
  shap_expected_value = shap_explainer.expected_value[-1]
  shaps = pd.DataFrame(
    data=shap_explainer.shap_values(df[features])[1],
    index=df.index,
    columns=features)
  return preds, shaps, shap_expected_value

例如，我們計算了該問題的 SHAP 值，得到了如下結果：

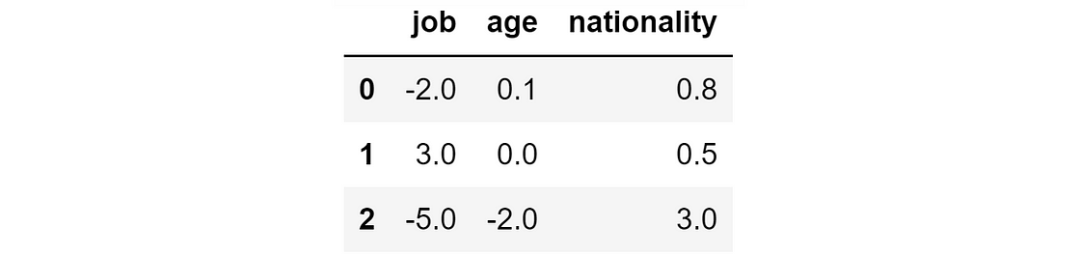模型預測的 SHAP 值

不過，就本文而言，只要知道以下幾點就足夠了：

• SHAP 正值：該特征導致該個體的概率增加；
• SHAP 負值：該特征導致該個體的概率降低。

因此，很明顯，個體的 SHAP 值總和與模型的預測之間存在直接關系。

然而，由于 SHAP 值可以是任何實際值（正值或負值），我們不能期望它等于對該個體的預測概率（即介于 0 和 1 之間的數字）。那么，SHAP 值總和與預測概率之間的關系是什么呢？

由于 SHAP 值可以是任何負值或正值，因此我們需要一個函數來將 SHAP 和轉化為概率。這個函數必須具備兩個特性

• 它應將任何實數值 "擠入" 區間 [0,1]；
• 它應該是嚴格遞增的（因為較高的 SHAP 和總是與較高的預測值相關聯）。

符合這些要求的函數就是 sigmoid 函數。因此，模型對某一行預測的概率等于該個體 SHAP 值總和的正余弦值。

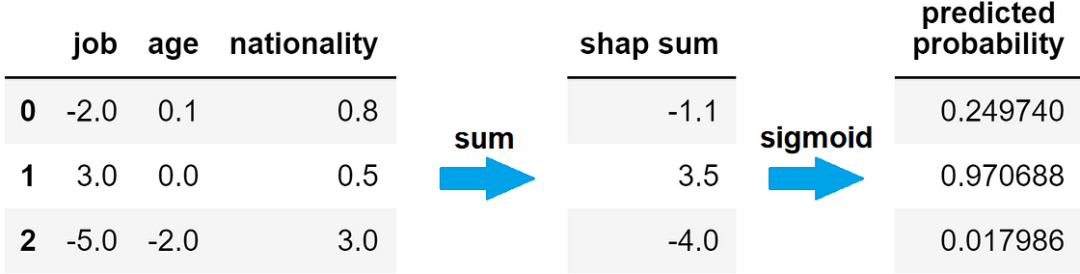從 SHAP 值到預測概率

下面是 sigmoid 函數的樣子：

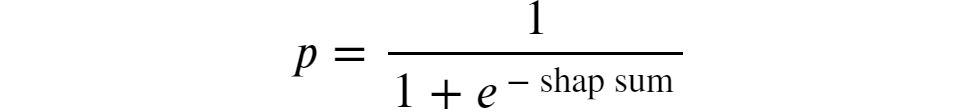圖片

那么，把這個公式轉換成一個 Python 函數：

def shap_sum2proba(shap_sum):
  """Compute sigmoid function of the Shap sum to get predicted probability."""
  
  return 1 / (1 + np.exp(-shap_sum))

還可以用圖形顯示出來，看看我們的個體在曲線上的位置：

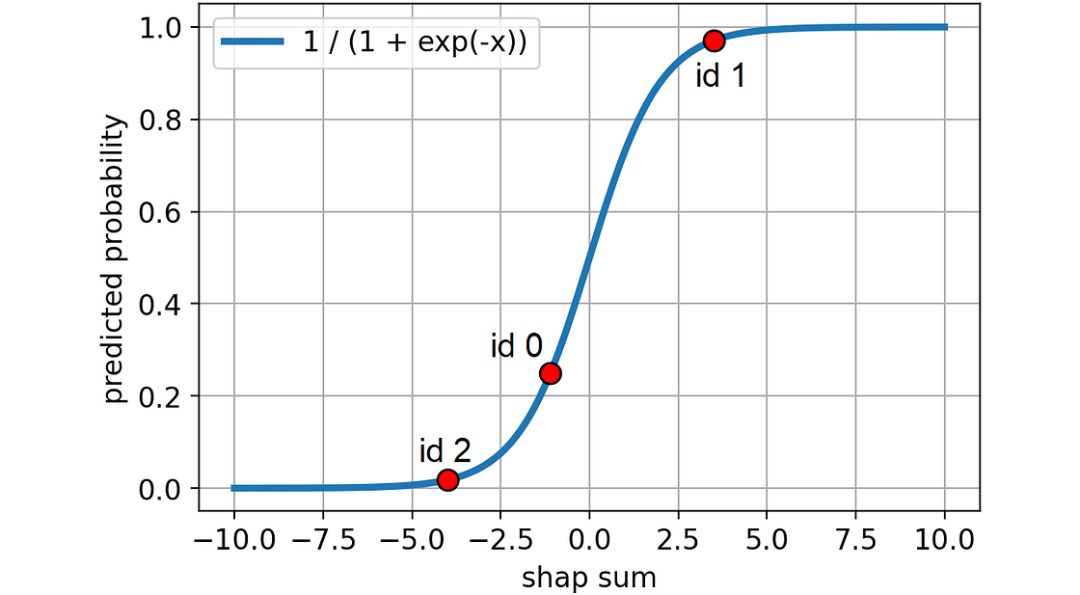圖片

既然我們已經了解了在分類問題中應該使用哪種誤差以及如何處理 SHAP 值，那么我們就可以看看如何計算預測值和誤差貢獻值了。

計算 "預測貢獻"

當 SHAP 值為高度正值（高度負值）時，預測結果會比沒有該特征時高（低）得多。換句話說，如果 SHAP 值的絕對值很大，那么該特征就會對最終預測結果產生很大影響。

這就是為什么我們可以通過取某一特征的 SHAP 絕對值的平均值來衡量該特征的預測貢獻。

prediction_contribution = shap_values.abs().mean()

在玩具數據集中，就得到了這樣的結果：

預測貢獻

因此，就特征的重要性而言，job是主要特征，其次是nationality，然后是age。

但誤差貢獻率如何呢？

5. 計算 "誤差貢獻"

"誤差貢獻" 背后的理念是計算如果我們去掉一個給定的特征，模型的誤差會是多少。

有了 SHAP 值，回答這個問題就很容易了：如果我們從 SHAP 總和中剔除某個特征，就可以得到模型在不知道該特征的情況下會做出的預測。但這還不夠：正如我們所看到的，要獲得預測概率，我們首先需要應用 sigmoid 函數。

因此，我們首先需要從 SHAP 總和中減去某個特征的 SHAP 值，然后再應用 sigmoid 函數。這樣，我們就得到了模型在不知道這些特征的情況下的預測概率。

在 Python 中，我們可以一次性完成所有特征的預測：

y_pred_wo_feature = shap_values.apply(lambda feature: shap_values.sum(axis=1) - feature).applymap(shap_sum2proba)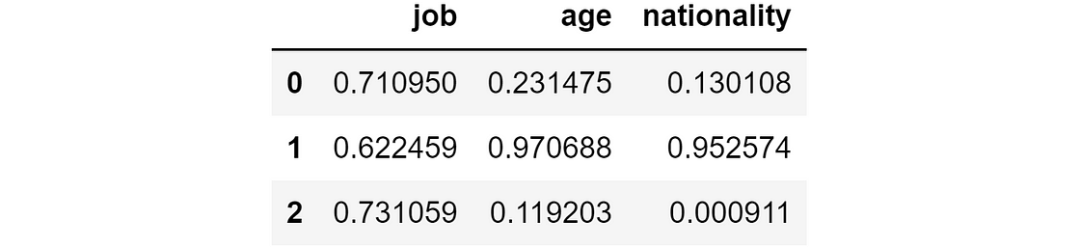

如果刪除相應特征，將得到的預測結果

這意味著，如果沒有job這一特征，模型預測第一個人的概率為 71%，第二個人的概率為 62%，第三個人的概率為 73%。相反，如果我們沒有nationality這一特征，預測結果將分別為 13%、95% 和 0%。

根據我們移除的特征，預測的概率相差很大。因此，得出的誤差（個體對數損失）也會大不相同。

我們可以使用上面定義的函數（"individual_log_loss"）來計算沒有相應特征時的個體對數損失：

ind_log_loss_wo_feature = y_pred_wo_feature.apply(lambda feature: individual_log_loss(y_true=y_true, y_pred=feature))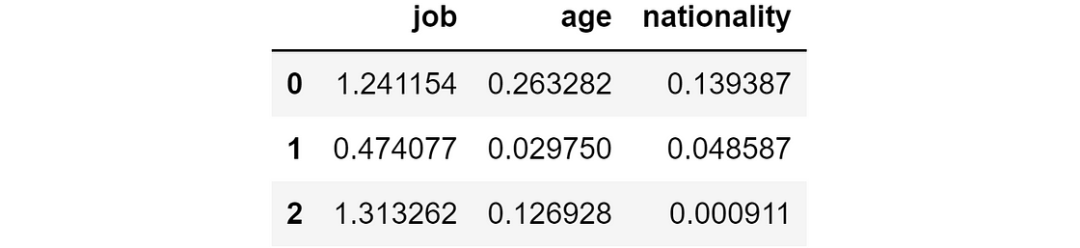

如果刪除相應特征，我們將獲得的單個對數損失

例如，如果我們選取第一行，我們可以看到，如果沒有job特征，對數損失將為 1.24，但如果沒有nationality特征，對數損失僅為 0.13。由于我們要盡量減少損失，在這種情況下，最好是去掉nationality這個特征。

現在，要知道有或沒有該特征的模型會更好，我們可以計算完整模型的單個對數損失與沒有該特征的單個對數損失之間的差值：

ind_log_loss = individual_log_loss(y_true=y_true, y_pred=y_pred)
ind_log_loss_diff = ind_log_loss_wo_feature.apply(lambda feature: ind_log_loss - feature)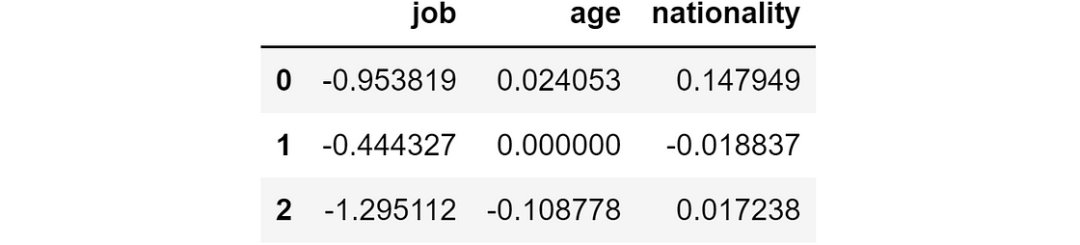

模型誤差與沒有該特征時的誤差之差

如果這個數字是

• 負數，則該特征的存在會導致預測誤差減小，因此該特征對該觀測結果非常有效。
• 正數，則該特征的存在會導致預測誤差增大，因此該特征對該觀測結果不利。

最后，我們可以按列計算出每個特征的誤差貢獻值，即這些值的平均值：

error_contribution = ind_log_loss_diff.mean()

錯誤貢獻

一般來說，如果這個數字是負數，則說明該特征具有積極作用；相反，如果這個數字是正數，則說明該特征對模型有害，因為它往往會增加模型的平均誤差。

在這種情況下，我們可以看到，模型中job特征的存在導致個體對數損失平均減少-0.897，而nationality特征的存在導致個體對數損失平均增加 0.049。因此，盡管nationality是第二重要的特征，但它的效果并不好，因為它會使平均個體對數損失增加 0.049。

將以上過程總結一個函數公后續使用：

def get_feature_contributions(y_true, y_pred, shap_values, shap_expected_value):
  """Compute prediction contribution and error contribution for each feature."""

  prediction_contribution = shap_values.abs().mean().rename("prediction_contribution")
  
  ind_log_loss = individual_log_loss(y_true=y_true, y_pred=y_pred).rename("log_loss")
  y_pred_wo_feature = shap_values.apply(lambda feature: shap_expected_value + shap_values.sum(axis=1) - feature).applymap(shap_sum2proba)
  ind_log_loss_wo_feature = y_pred_wo_feature.apply(lambda feature: individual_log_loss(y_true=y_true, y_pred=feature))
  ind_log_loss_diff = ind_log_loss_wo_feature.apply(lambda feature: ind_log_loss - feature)
  error_contribution = ind_log_loss_diff.mean().rename("error_contribution").T
  
  return prediction_contribution, error_contribution

真實數據集示例

具體代碼可參考上一篇內容：

下面，我將使用來自Pycaret的數據集。該數據集名為 "Gold"，包含一些金融數據的時間序列。

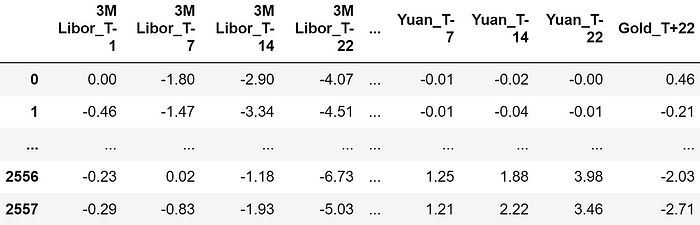數據集樣本。特征均以百分比表示，因此 -4.07 表示回報率為 -4.07%

特征包括觀察時刻前 22 天、14 天、7 天和 1 天（"T-22"、"T-14"、"T-7"、"T-1"）的金融資產回報率。以下是用作預測特征的所有金融資產：

圖片

可用資產列表。每種資產的觀測時間分別為-22、-14、-7 和-1。

我們總共有 120 個特征。

我們的目標是預測黃金未來 22 天的回報率是否會大于 5%。換句話說，目標變量是0/1變量的：

• 0，如果黃金未來 22 天的回報率小于 5%；
• 1，如果黃金未來 22 天的回報率大于 5%。

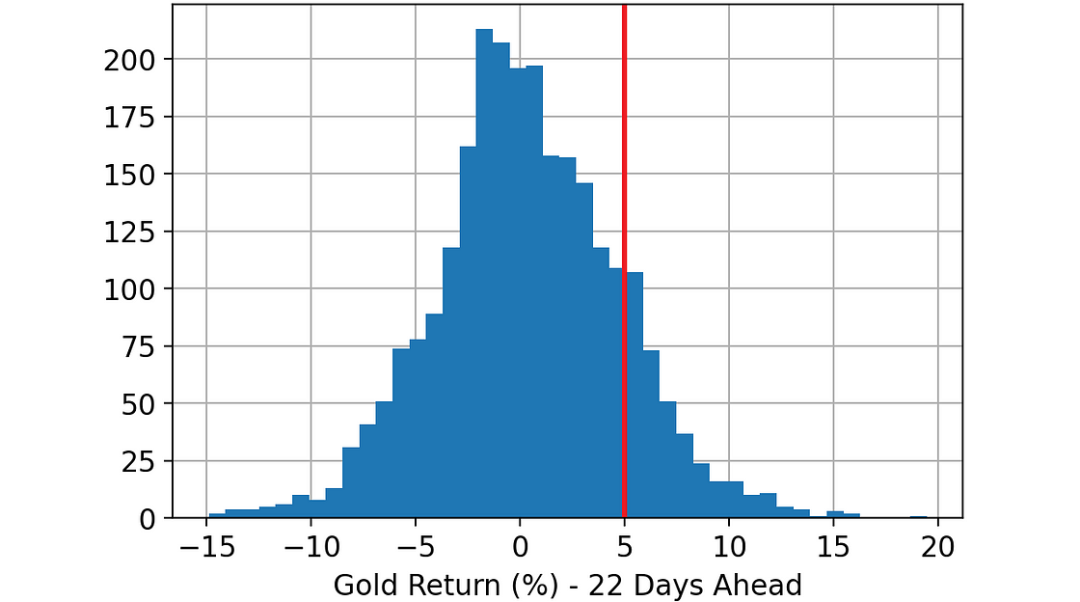圖片

未來 22 天黃金回報率柱狀圖。標為紅色的閾值用于定義我們的目標變量：回報率是否大于 5%

加載數據集后，我執行了以下步驟：

1. 隨機分割整個數據集：33% 的行在訓練數據集中，另外 33% 在驗證數據集中，剩下的 33% 在測試數據集中。
2. 在訓練數據集上訓練 LightGBM 分類器。
3. 使用上一步訓練的模型對訓練、驗證和測試數據集進行預測。
4. 使用 Python 庫 "shap "計算訓練、驗證和測試數據集的 SHAP 值。
5. 使用我們在上一段中看到的代碼，計算每個特征在每個數據集（訓練集、驗證集和測試集）上的預測貢獻值和誤差貢獻值。

至此，我們就有了預測貢獻值和誤差貢獻值，可以對它們進行比較了：

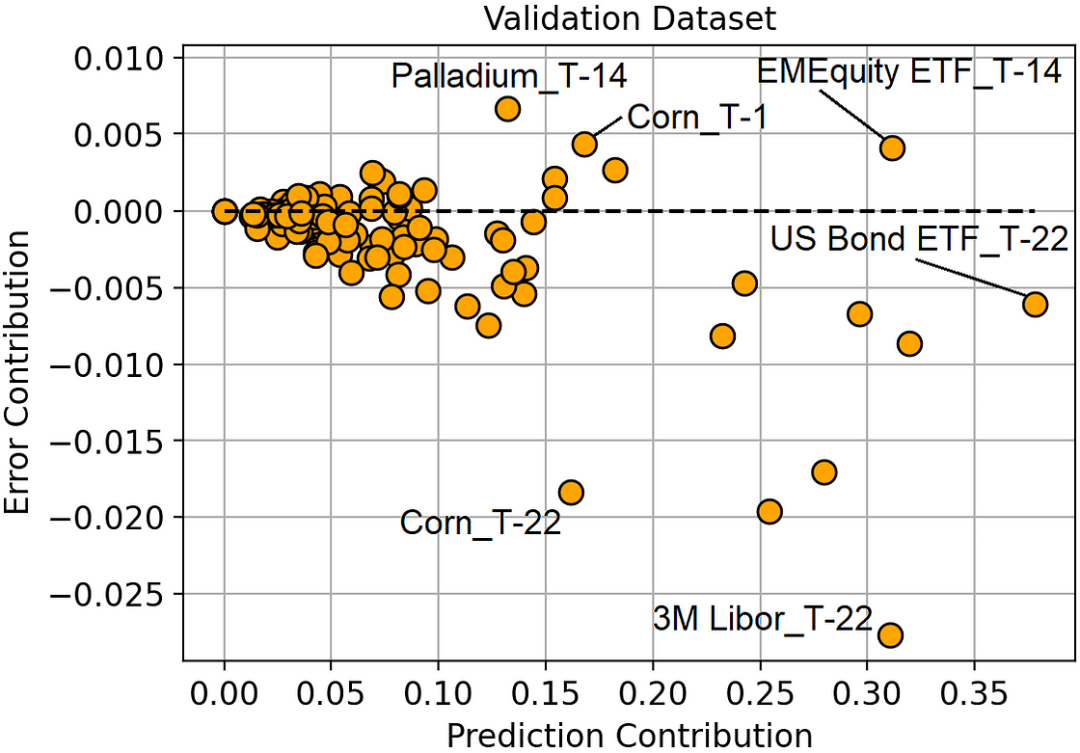預測貢獻與誤差貢獻（驗證數據集）

通過觀察這幅圖，我們可以對模型有寶貴的了解。

最重要的特征是 T-22 天的美國債券 ETF，但它并沒有帶來如此大的誤差減少。最好的特征是 T-22 日的 3M Libor，因為它能最大程度地減少誤差。

玉米價格有一些非常有趣的地方。T-1 期和 T-22 期的收益率都是最重要的特征之一，但其中一個特征（T-1 期）是過度擬合的（因為它會使預測誤差變大）。

一般來說，我們可以觀察到所有誤差貢獻較大的特征都是相對于 T-1 或 T-14（觀察時刻前 1 天或 14 天）而言的，而所有誤差貢獻較小的特征都是相對于 T-22（觀察時刻前 22 天）而言的。這似乎表明，最近的特征容易過度擬合，而較早回報的特征往往概括性更好。

除了深入了解模型之外，我們還可以很自然地想到使用誤差貢獻來進行特征選擇。這就是我們下一段要做的。

"誤差貢獻"進行遞歸特征消除

遞歸特征消除（RFE）是從數據集中逐步去除特征的過程，目的是獲得更好的模型。

RFE 算法非常簡單：

1. 初始化特征列表；
2. 使用當前特征列表作為預測因子，在訓練集上訓練一個模型；
3. 從特征列表中刪除 "最差 "特征；
4. 回到第 2 步（直到特征列表為空）。

在傳統方法中，"最差" = 最不重要。然而，根據我們的觀察，我們可能會反對先刪除危害最大的特征。

換句話說

• 傳統的 RFE：先去除最無用的特征（最無用 = 驗證集上最低的預測貢獻）。
• 我們的 RFE：先去除最有害的特征（最有害 = 驗證集上最高的誤差貢獻）。

為了驗證這種直覺是否正確，我使用這兩種方法進行了模擬。

這是驗證集上的對數損失結果：

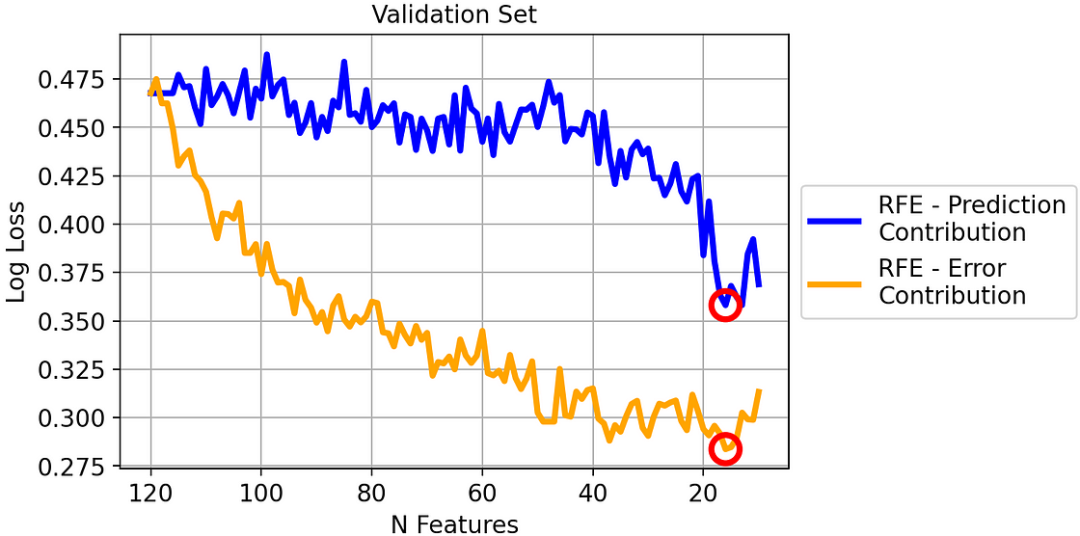兩種策略在驗證集上的對數損失

由于對數損失是一個 "越低越好 "的指標，我們可以看到，在驗證數據集上，我們的 RFE 版本明顯優于經典 RFE。

不過，你可能會懷疑，只看驗證集并不公平，因為誤差貢獻是在驗證集上計算的。那么，我們來看看測試集。

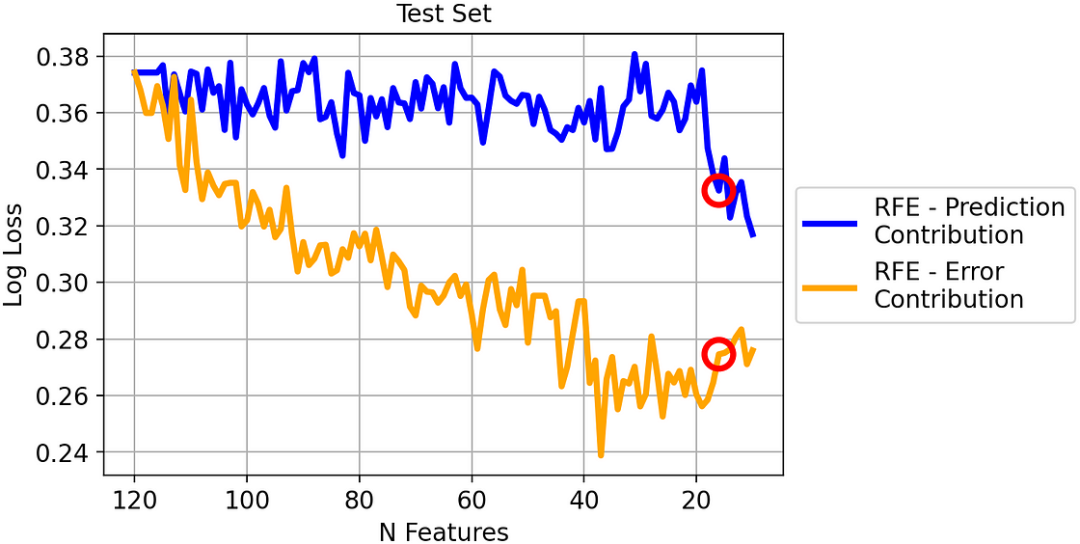兩種策略在測試集上的對數損失

即使現在兩種方法之間的差距變小了，但我們可以看到差距仍然很大，因此足以得出結論：在這個數據集上，基于誤差貢獻的 RFE 明顯優于基于預測貢獻的 RFE。

除了對數損失，我們還可以考慮一種更有實用價值的指標。例如，我們來看看驗證集上的平均精度：

兩種策略在驗證集上的平均精確度

值得注意的是，盡管貢獻誤差是基于對數損失計算的，但我們在平均精度方面也取得了很好的結果。

如果我們想根據平均精度做出決定，那么我們就會選擇驗證集上平均精度最高的模型。這意味著：

• 基于誤差貢獻的 RFE：具有 19 個特征的模型；
• 基于預測貢獻的 RFE：具有 14 個特征的模型；

如果我們這樣做，在新數據上會觀察到什么性能？回答這個問題的最佳代表就是測試集：

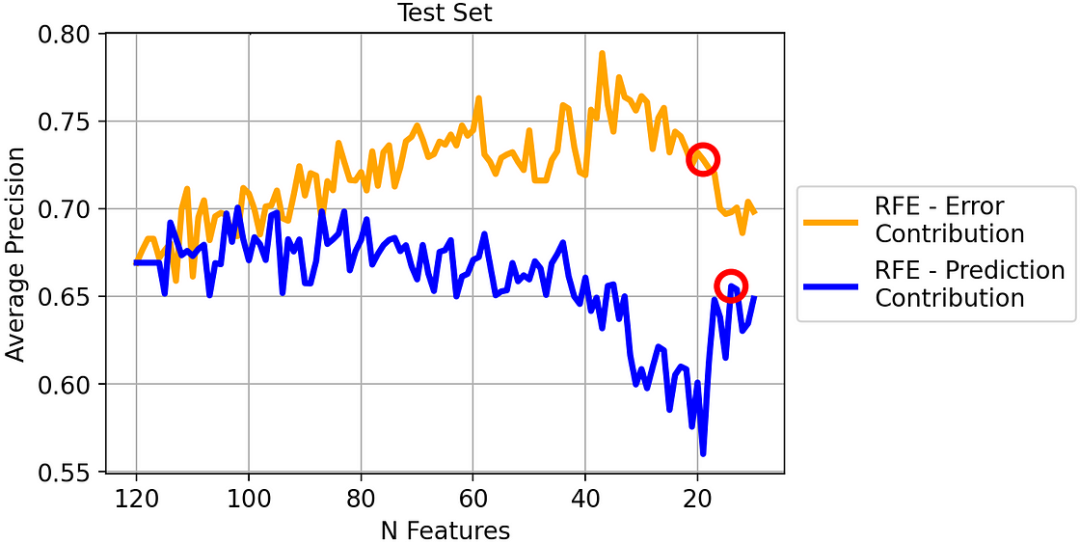圖片

兩種策略在驗證集上的平均精確度

同樣在這種情況下，基于誤差貢獻的 RFE 性能總體上優于基于預測貢獻的 RFE。特別是，根據我們之前的判斷：

• 基于誤差貢獻的 RFE（包含 19 個特征的模型）： 平均精確度為 72.8%；
• 基于預測貢獻的 RFE（模型有 14 個特征）：平均精度為 65.6%： 平均精度為 65.6%。

因此，通過使用基于誤差貢獻的 RFE，而不是傳統的基于預測貢獻的 RFE，我們可以在平均精確度上額外獲得 7.2% 的顯著提高！

結論

特征重要性的概念在機器學習中扮演著重要角色。然而，"重要性" 的概念常常被誤認為是 "好"。

為了區分這兩個方面，我們引入了兩個概念： 預測貢獻和誤差貢獻。這兩個概念都基于驗證數據集的 SHAP 值，在文章中我們看到了計算它們的 Python 代碼。

我們還在一個真實的金融數據集（其中的任務是預測黃金價格）上對它們進行了嘗試，結果證明，與傳統的基于預測貢獻的 RFE 相比，基于誤差貢獻的遞歸特征消除可使平均精度提高 7%。