RAG真能提升LLM推理能力?人大最新研究:數據有噪聲,RAG性能不升反降
近年來,大語言模型已經在多種任務上表現出來出色的能力,然而,由于缺乏事實性信息,當前的LLM經常出現嚴重的幻覺現象;此外,LLM中的知識是通過其參數進行編碼記憶,這意味著要融入新知識需要進一步的微調,消耗大量的時間與計算資源。因此,通過結合外部檢索器來增強LLM的性能,已經成為了主流的方案。
盡管RAG在現代LLM中被廣泛采用,但對于RAG如何輔助推理的深入理解仍然是一個未解的問題。目前,大多數研究人員主要將RAG視為提供領域特定知識的方法,并常常試圖通過RAG使LLM適應特定子領域。然而,RAG在增強推理能力方面的影響尚未得到深入研究。
近日,來自中國人民大學的學者指出,RAG可以幫助LLM提升其推理能力,但其提升有限,并且由于retriever中的噪聲,RAG甚至可能造成推理能力的下降。
 圖片
圖片
論文地址:https://export.arxiv.org/abs/2410.02338
背景與動機
我們可以將LLM視為計算 ??(??∣??),其中q 代表問題query,??是相應的答案。
在這種情況下,檢索增強生成(RAG)可以表示為 ??(??∣??,??1,??2,…,????),其中 ???? 是基于query ??檢索到的第 ?? 個文檔。
此外,眾所周知的prompt方法「思維鏈」(CoT)顯著增強了LLMs的推理能力,它可以表示為 ??(??∣??,??1,??2,…,????),其中 ???? 表示逐步推理的結果。CoT和RAG都旨在將額外的信息融入到輸入中,以獲得更好的性能。理論上和實驗上都已證明,CoT能夠有效提升LLMs的推理能力。那么問題是:RAG是否也能增強LLMs的推理能力?
由于LLM的層數有限,其推理能力局限于固定深度。當將推理路徑概念化為一棵樹時,其最大深度保持不變。思維鏈(Chain of Thought, CoT)通過逐步推理或解釋來生成答案,而不是直接提供答案,其形式化表達為 ??1=??(??), ??2=??(??,??1),…,??=??(??,??1,…,????)。
這一過程允許CoT通過多次執行??來有效擴展推理深度,隨著CoT步驟的增加,潛在地達到無限深度。
相比之下,檢索增強生成(RAG)并不支持多次推理;它檢索現有的相關信息來生成答案,因此無法堆疊transformer層數。
雖然RAG不能通過堆疊LLM層數來增強推理能力,但檢索到的文檔可能包含中間推理結果,從而減少了推理所需的層數,使LLM能夠處理更復雜的問題,進而幫助提升其推理能力。
樹形推理結構
對于一個具有 ??層的推理樹 ??,令第 ?? 層的節點數量為 ????,并將第 ?? 層的第 ?? 個節點表示為 ????,??。檢索到的文檔 ?? 包含的相關信息可以用來替換某些推理節點的內容。
例如,考慮query「Who is the actor playing Jason on General Hospital?」。
在這種情況下,可能存在一個節點 ????,??,它表示關于「what is General Hospital?」的信息。如果我們提供一個包含「General Hospital」詳細信息的文檔,那么 ????,?? 的計算就可以通過從該文檔中提取相關信息來有效替代。
該文檔不僅簡化了 ????,?? 的計算,還消除了所有僅與 ????,?? 相連的節點。這些節點只對 ????,?? 的推理有貢獻,既然 ????,?? 的信息可以直接從文檔中得出,那么它們的推理就變得不必要了。因此,檢索到與節點 ????,?? 相關的單個文檔可能會減少多個下層節點的存在。這一過程類似于核武器中的裂變反應,減少一個節點會觸發其他多個節點的減少。
因此,如果某一層 ??′ 的所有節點都通過檢索增強生成(RAG)方法被簡化,任何 ??≤??′ 的層都可以被消除,從而有效降低整體的推理深度。
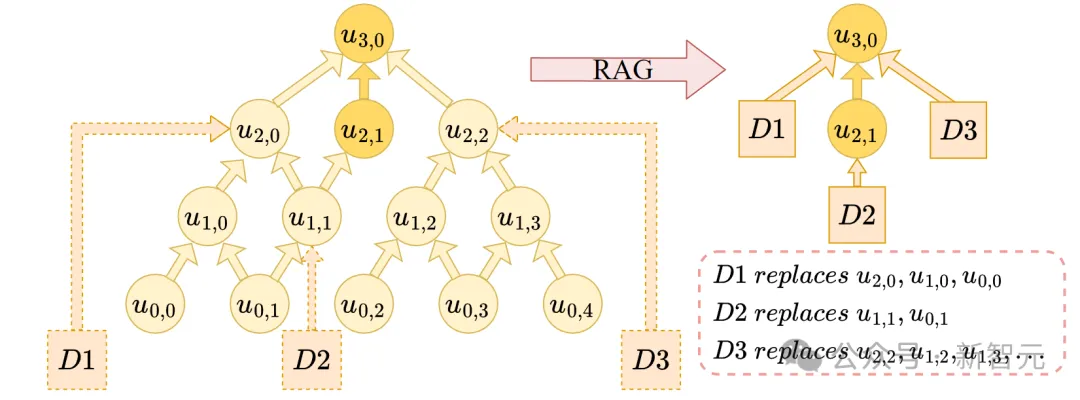 圖片
圖片
如上圖所示,推理樹由4層組成,我們檢索到了3個文檔 ??1, ??2, ??3,分別為節點 ??2,0、??1,1 和 ??2,2 提供了信息。
通過文檔 ??1,節點 ??1,0 也可以被移除,因為它只對 ??2,0 有貢獻;通過文檔 ??2,??0,1 也不再需要;由于文檔 ??3,節點 ??1,2 和 ??1,3也可以唄移除。
因此,第一層的所有4個節點都可以通過文檔信息消除,這意味著第一層和第零層的所有節點都是不必要的。這樣,推理深度從4層減少到了2層。因此,借助相關文檔,RAG可以有效降低問題的推理復雜度,使LLM能夠解決更復雜的問題。
我們可以觀察到,消除單個節點會顯著影響較淺層中的許多節點,類似于裂變反應。如果這種裂變過程能夠無限擴展,RAG可能會大大增強LLMs的推理能力。
然而,如果裂變反應在某個閾值處停止,其效果可能會受到限制。因此,為了評估RAG能夠減少多少層,關鍵在于確定這一類似裂變的過程是否會終止。理解這一動態對于評估RAG如何提升推理能力以及LLMs在復雜問題求解中的整體效率至關重要。
顯然,針對第??層,該層節點被erase的概率由兩個部分組成,一是由于上層節點的推理不再需要,二是某個文檔中包含該節點的信息,假設某個文檔中包含該節點的信息的概率為一個常數??
p,并且在第??+1層中有????+1%被消除,那么第??層節點被消除的概率可以是????=??(????+1)=??(??).
令 ??(??)=??(??)???,表示第 ?? 層的增長,可以考慮在 (0,1) 區間內存在一個點 ??^,使得 ??(??^)=0。
如果在 ??>??^時,??(??)<0,表明被消除的節點數預期會比前一層更少,意味著裂變反應不會無限傳播,而是會達到一個臨界閾值。超過這一點后,下一層被消除的節點數預計會比當前層減少,從而限制裂變反應的擴展。
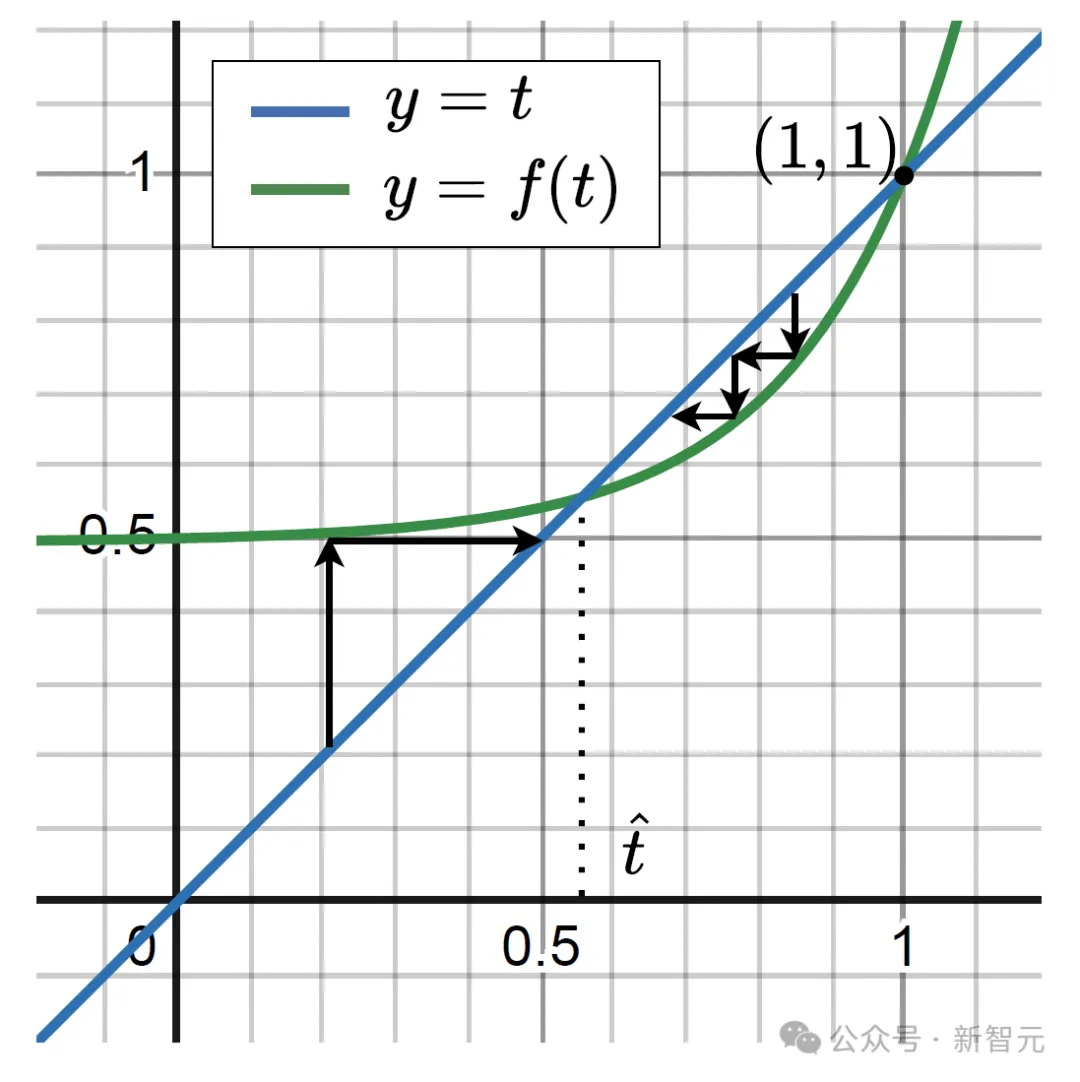 圖片
圖片
由上圖可見,當 ??^存在時,節點被erase的概率會逐漸收斂到 ??^,無法無限擴張下去,同時 ??^的位置取決于層與層之間連接的系數程度和某個文檔中包含節點的信息的概率。當層與層之間連接十分稀疏時或者retriever的性能很強,那么就可以使 ??^>1,那么節點被erase的概率就會收斂到1,即可erase一整個layer從而降低問題所需的推理深度,使LLM可以解決更復雜的問題。
文檔噪聲
然而,在實際的RAG場景中,從文檔中檢索到的信息并不總是可以直接使用,通常需要進一步處理,因為文檔可能包含噪聲信息,而且有些文檔甚至可能包含錯誤的答案。這些噪聲和干擾文檔會對性能產生負面影響。
雖然一些研究嘗試微調模型以過濾噪聲和干擾文檔,但該方法使LLM先完成過濾再進行推理,降低了推理能力。此外,一些研究訓練另一個過濾模型,但這種方法會導致額外的推理成本,并且無法消除文檔中內涵的固有噪聲。
因此,出現了一個關鍵問題:過濾無關文檔是否困難,我們能否在有限的層數內有效解決它? 如果過濾噪聲所需的成本甚至超過了RAG帶來的幫助,那么RAG將無法提升推理能力。
令 ?? 表示標記的相關性,????=0 表示標記 第 ??個token ????是噪聲,否則該token是相關的。
令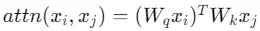 表示LLM的原始注意力層。我們假設期望的自注意力函數為:
表示LLM的原始注意力層。我們假設期望的自注意力函數為:
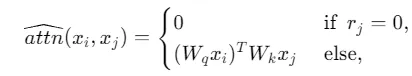 圖片
圖片
對模型的微調可以表示為
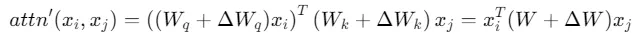 圖片
圖片
其中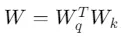 ,ΔW 表示其余項。
,ΔW 表示其余項。
在這種情況下,如果我們需要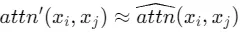 , 我們需要對于所有的相關的token ????,有
, 我們需要對于所有的相關的token ????,有
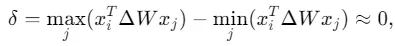
因此,需要對于所有的相關token,有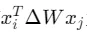 為一個常數,才可以使得
為一個常數,才可以使得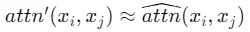 。
。
Triple-Wise Problem
對于輸入序列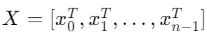 , ?? 表示每個token的相關性。
, ?? 表示每個token的相關性。
具體來說,對于每個token ????,相關性得分 ????=0 表示該標記與查詢無關。
需要注意的是,計算 ????不僅僅依賴于該token ????和query;相反,它可能需要涉及三個或更多token。
例如,假設輸入為「Alice is exhausted, but Bob is still very excited, showing no signs of fatigue. How does Bob feel?」,單詞「exhausted」是一個噪聲token,應在推理過程中排除。
然而,確定該token的相關性需要考慮query中的「Bob」以及「exhausted」的主語「Alice」。因此,識別一個標記的相關性需要來自多個token的信息,而自注意力機制僅在成對之間計算關系,這使得在單個transformer層內解決此問題變得困難。
在檢索增強生成(RAG)場景中,我們可以簡化這個triple wise problem。通過預先計算文檔中的信息,并將這些匯總信息表示為一個或幾個額外的token(virtual token),我們可以僅使用來自token本身、query和virtual token的信息來評估標記的相關性。在這種情況下,使triple wise problem變為了pair-wise problem。
在判斷token ????是否相關時,不再需要遍歷所有的輸入token ????以尋找和query的沖突,僅需遍歷所有的virtual token即可。
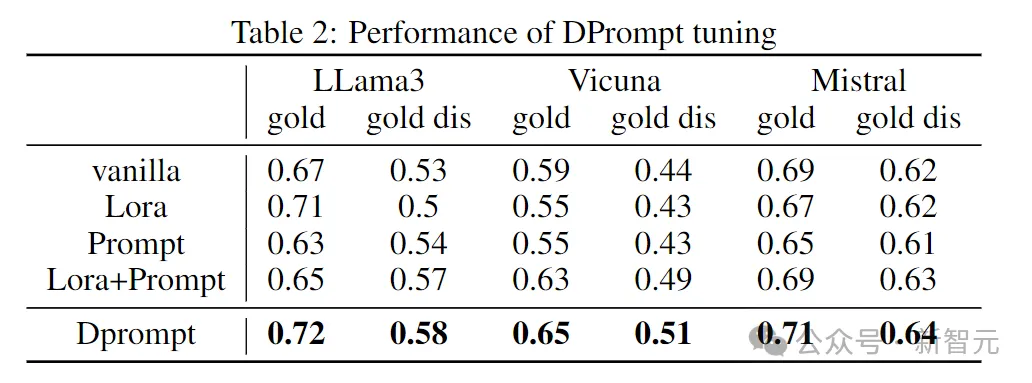
我們微調一個bert模型以獲取文檔的表征,并通過MLP將其映射到合適的維度,將其作為virtual token插入到模型的輸入prompt中進行微調,實驗結果如下
 圖片
圖片
其中gold代表document中只包含一個文檔,該文檔直接包含了query的答案,但該文檔中仍然存在一定的噪聲;gold dis代表文檔中包含gold文檔以及distracting文檔,distracting文檔中包含錯誤的答案。由上圖可見,DPrompt tuning有效提升了LLM在面對噪聲時的性能。
參考資料:
https://arxiv.org/html/2410.02338v2









































