深入理解多重共線性:基本原理、影響、檢驗與修正策略
在數據科學和機器學習領域,構建可靠且穩健的模型是進行準確預測和獲得有價值見解的關鍵。然而當模型中的變量開始呈現出高度相關性時,就會出現一個常見但容易被忽視的問題 —— 多重共線性。多重共線性是指兩個或多個預測變量之間存在強相關性,導致模型難以區分它們對目標變量的貢獻。如果忽視多重共線性,它會扭曲模型的結果,導致系數的可靠性下降,進而影響決策的準確性。本文將深入探討多重共線性的本質,闡述其重要性,并提供有效處理多重共線性的方法,同時避免數據科學家常犯的陷阱。
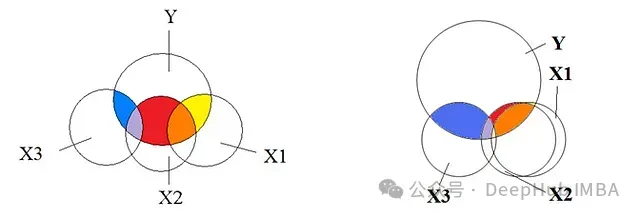
多重共線性的定義
多重共線性是指數據集中兩個或多個自變量(預測變量)之間存在強烈的線性相關性。簡而言之,這些自變量包含了重疊的信息,而不是提供預測因變量(目標變量)所需的唯一信息,使得模型難以確定每個自變量的individual貢獻。
在回歸分析中,自變量(independent variable)是影響結果的因素,而因變量(dependent variable)是我們試圖預測的結果。舉個例子,在房價預測模型中,房屋面積、臥室數量和地理位置等因素被視為自變量,而房價作為因變量,取決于這些自變量的變化。
為了充分理解多重共線性的影響,我們需要先了解線性回歸的一些知識。
線性回歸
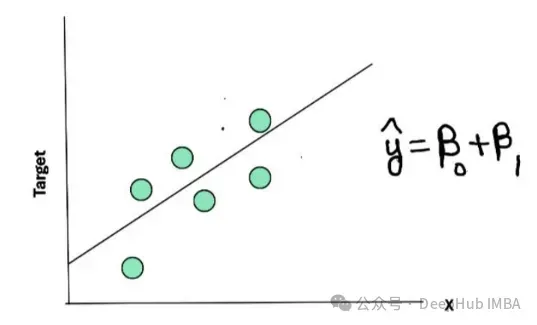
假設我們有一組用綠點表示的數據,我們希望通過這些點擬合一條直線來進行預測。穿過這些點的直線被稱為回歸線,它對數據進行了概括和總結。
在這個簡單的例子中,目標變量(房價)是因變量,我們使用一個自變量(如房屋面積)來預測它。一個簡單線性回歸的方程可以表示為:
? = β? + β?X
其中:
- ? 表示預測值(回歸線上的一個點)。
- X 表示自變量的值。
- β? 表示截距(回歸線與y軸的交點)。
- β? 表示斜率(回歸線的斜率)。
實際數據點與預測值(?)之間的差異被稱為殘差(residual)或誤差(error):
殘差 = y? - ??
其中:
- y? 表示第i個觀測值的實際值。
- ?? 表示第i個觀測值的預測值。
線性回歸的目標是通過最小化殘差平方和來找到最佳擬合直線,使得預測值與實際值之間的差異最小。
多個自變量的情況
在多元線性回歸中,我們使用多個自變量來預測因變量,其方程可以表示為:
? = β? + β?X? + β?X? + … + β?X?
其中:
- X?, X?, …, X? 表示不同的自變量(如房屋面積、臥室數量、地理位置等)。
- β?, β?, …, β? 表示各個自變量對應的回歸系數。
我們希望每個自變量對目標變量有其獨特的貢獻。雖然因變量與自變量之間的相關性是我們所期望的,但自變量之間的相關性卻是我們需要避免的。例如,我們不希望出現以下情況:
X? = β? + β?X?
這就是多重共線性的表現 —— 自變量之間表現出類似因變量的線性關系,給模型的訓練和推斷帶來了混淆和不確定性。
為何需要處理多重共線性?
讓我們通過一個簡單的例子來理解多重共線性的影響。考慮以下用于預測目標變量?的方程:
? = 10 + 2X? + 5X?
假設 X? 和 X? 之間存在強相關性,我們可以將它們的關系表示為:
X? = X? + 1
那么,原始方程可以轉化為以下兩種形式:
- ? = 12 + 0X? + 9X?
- ? = 7.5 + 4.5X? + 0X?
現在,我們有三個不同的方程來預測 ? ,這導致模型產生了混淆:
- 截距項(intercept)應該是10、12還是7.5?
- X? 和 X? 的系數(coefficients)應該如何確定?
由于 X? 和 X? 之間的相關性,回歸系數變得不穩定和不可靠。隨著多重共線性程度的增加,模型中的系數估計會出現更大的波動,導致模型的不穩定和不可靠。這種不確定性使得我們難以解釋自變量和因變量之間的真實關系,這就是為什么有效處理多重共線性至關重要。
選擇合適的多重共線性處理方法
處理多重共線性有多種有效的方法。以下是一些常用的技術:
- 從相關變量對中移除一個特征: 如果兩個變量高度相關,可以考慮移除其中一個,以減少冗余信息。
- 檢查方差膨脹因子(VIF): 識別具有高VIF值的特征,這表明存在多重共線性。移除高VIF特征有助于提高模型的穩定性。
- 使用主成分分析(PCA)進行數據轉換: PCA通過創建原始變量的線性組合來降低數據維度,從而消除多重共線性。
- 應用嶺回歸(Ridge Regression)或Lasso回歸: 這些正則化技術通過收縮回歸系數來減輕多重共線性的影響。嶺回歸通過最小化系數的L2范數來實現,而Lasso回歸則通過最小化系數的L1范數,可以將一些系數壓縮為零。
需要避免的常見錯誤
- 盲目移除相關特征: 這種方法在只有少數特征相關的情況下是可行的,但如果存在大量相關特征,則可能不太實用。
- 過度依賴PCA: 盡管PCA在減輕多重共線性方面非常有效,但新生成的變量可解釋性較差,這使得向非技術利益相關者解釋結果變得更具挑戰性。
- 對嶺回歸和Lasso回歸的誤解: 雖然這些方法可以減輕多重共線性的影響,但它們主要是正則化技術。它們并不能完全"治愈"多重共線性,而是通過調整系數來幫助控制其影響。
考慮到這些局限性,我們通常會將 方差膨脹因子(VIF) 作為識別和處理多重共線性的最有效工具之一。VIF可以幫助我們確定導致多重共線性的特征,從而做出明智的決策,在保持模型可解釋性的同時提高其穩定性。
方差膨脹因子(VIF)
方差膨脹因子(VIF)是一種統計度量,用于檢測回歸模型中是否存在多重共線性。它量化了由于自變量之間的多重共線性而導致的回歸系數方差的膨脹程度。VIF告訴我們其他自變量對特定預測變量方差的影響程度。
為了更好地理解VIF,讓我們先回顧一下回歸分析中的一個關鍵概念:決定系數(coefficient of determination),也稱為R2。R2用于評估回歸模型對數據的擬合優度。例如,R2 = 0.9意味著目標變量(?)中90%的變異可以由模型中的自變量解釋。
VIF的工作原理
VIF通過以下步驟幫助我們識別和消除模型中的多重共線性:
步驟1: 對每個自變量建立一個線性回歸模型,使用數據集中的其他自變量作為預測變量。這意味著我們不是直接預測目標變量(?),而是嘗試用其他自變量來解釋每個自變量。
例如:
- X? = αX? + αX? + … + αX?
- X? = θX? + θX? + … + θX?
- X? = δX? + δX? + … + δX?
在VIF的計算過程中,我們為每個自變量擬合一個線性回歸模型,使用數據集中其余的自變量作為預測變量。
步驟2: 對于每個線性回歸模型,我們計算決定系數R2。這給出了每個自變量的R2值(記為R2?),表示其他自變量能夠解釋該自變量變異性的程度。
步驟3: 使用以下公式計算每個自變量的VIF:
- VIF? = 1 / (1 - R2?)
這個公式表明,當R2?增加時,VIF也會隨之增加。例如:
- 如果R2? = 1,則VIF? = ∞(完全多重共線性)。
- 如果R2? = 0.9,則VIF? = 10。
- 如果R2? = 0.8,則VIF? = 5。
VIF值較高表示該自變量與其他自變量高度共線,這可能會扭曲回歸系數的估計。
基于VIF的特征選擇
基于VIF的特征選擇通常以迭代的方式進行。這意味著我們每次移除一個具有高VIF值的特征,然后重新計算剩余特征的VIF值。重復這個過程,直到所有特征的VIF值都低于設定的閾值(通常為5或10)。
由于移除一個特征會影響其他特征之間的多重共線性,因此在每次移除后重新計算VIF值很重要,以確保模型逐步變得更加穩定和可靠。
Python代碼示例
以下是一段使用Python實現VIF計算和基于VIF的特征選擇的代碼示例:
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant
def calculate_vif(X):
"""
計算給定自變量矩陣X的方差膨脹因子(VIF)
"""
# 添加常數項
X = add_constant(X)
# 計算每個特征的VIF
vif = pd.Series([variance_inflation_factor(X.values, i)
for i in range(X.shape[1])],
index=X.columns)
return vif
def vif_feature_selection(X, threshold=5):
"""
基于VIF的特征選擇
"""
vif = calculate_vif(X)
while vif.max() > threshold:
# 移除具有最大VIF值的特征
feature_to_remove = vif.idxmax()
X = X.drop(columns=[feature_to_remove])
# 重新計算VIF
vif = calculate_vif(X)
return X
# 使用示例
selected_features = vif_feature_selection(X)在這個示例中,我們定義了兩個函數:
- calculate_vif(X):計算給定自變量矩陣X的VIF值。它首先為X添加一個常數項,然后使用variance_inflation_factor()函數計算每個特征的VIF。
- vif_feature_selection(X, threshold=5):基于VIF進行特征選擇。它重復計算VIF并移除具有最大VIF值的特征,直到所有特征的VIF值都低于給定的閾值(默認為5)。
這段代碼演示了如何使用VIF進行多重共線性檢測和特征選擇的完整過程。將其應用于自己的數據集,以識別和處理多重共線性問題。
總結
理解和處理多重共線性對于構建可靠和可解釋的回歸模型至關重要。當自變量之間存在高度相關性時,可能導致回歸系數估計不穩定、標準誤差膨脹以及模型預測不可靠。通過使用移除相關特征、主成分分析(PCA)、嶺回歸或Lasso回歸等技術,我們可以有效地減輕多重共線性的影響。
在眾多處理多重共線性的方法中,方差膨脹因子(VIF)脫穎而出,成為識別和量化多重共線性影響的實用工具。通過計算每個自變量的VIF值,我們能夠確定導致多重共線性的特征,并采取相應的措施,以確保模型的穩健性和可解釋性。
總的來說,恰當地處理多重共線性可以提高模型的性能,增強結果的可解釋性,并確保我們的預測建立在穩定可靠的系數估計之上。通過有策略地應用這些方法,我們能夠構建出不僅準確,而且更加可靠和易于理解的模型。