HuggingFace工程師親授:如何在Transformer中實現最好的位置編碼
在 Transformer 模型中,位置編碼(Positional Encoding) 被用來表示輸入序列中的單詞位置。與隱式包含順序信息的 RNN 和 CNN 不同,Transformer 的架構中沒有內置處理序列順序的機制,需要通過位置編碼顯式地為模型提供序列中單詞的位置信息,以更好地學習序列關系。
位置編碼通常通過數學函數生成,目的是為每個位置生成一個獨特的向量。這些向量在嵌入空間中具有特定的性質,比如周期性和連續性。
在最近的一篇文章中,HuggingFace 機器學習工程師 Christopher Fleetwood 介紹了逐步發現 Transformer 模型中最先進位置編碼的方法。為此,作者會講述如何不斷改進位置編碼方法,最終形成旋轉位置編碼 (RoPE),并在最新的 LLama 3.2 版本和大多數現代 Transformer 中使用。在讀這篇文章前,你需要掌握一些基本的線性代數、三角學和自注意力的知識。
問題陳述
與所有問題一樣,最好首先了解我們想要實現的目標。Transformer 中的自注意力機制用于理解序列中 token 之間的關系。自注意力是一種集合運算,這意味著它是置換等變的。如果我們不利用位置信息來豐富自注意力,就無法確定許多重要的關系。
舉例說明最能說明這一點。
考慮一下這個句子,其中同一個單詞出現在不同的位置:
「這只狗追趕另一只狗」
直觀地看,「狗」指的是兩個不同的實體。如果我們首先對它們進行 token 化,映射到 Llama 3.2 1B 的真實 token 嵌入,并將它們傳遞給 torch.nn.MultiheadAttention ,會發生什么。
import torchimport torch.nn as nnfrom transformers import AutoTokenizer, AutoModelmodel_id = "meta-llama/Llama-3.2-1B"tok = AutoTokenizer.from_pretrained(model_id)model = AutoModel.from_pretrained(model_id)text = "The dog chased another dog"tokens = tok(text, return_tensors="pt")["input_ids"]embeddings = model.embed_tokens(tokens)hdim = embeddings.shape[-1]W_q = nn.Linear(hdim, hdim, bias=False)W_k = nn.Linear(hdim, hdim, bias=False)W_v = nn.Linear(hdim, hdim, bias=False)mha = nn.MultiheadAttention(embed_dim=hdim, num_heads=4, batch_first=True)with torch.no_grad(): for param in mha.parameters(): nn.init.normal_(param, std=0.1) # Initialize weights to be non-negligibleoutput, _ = mha(W_q(embeddings), W_k(embeddings), W_v(embeddings))dog1_out = output[0, 2]dog2_out = output[0, 5]print(f"Dog output identical?: {torch.allclose(dog1_out, dog2_out, atol=1e-6)}") #True可以看到,如果沒有任何位置信息,那么(多頭)自注意力運算的輸出對于不同位置的相同 token 是相同的,盡管這些 token 顯然代表不同的實體。
讓我們開始設計一種利用位置信息增強自注意力的方法,以便它可以確定按位置編碼的單詞之間的關系。
為了理解和設計最佳編碼方案,讓我們探討一下這種方案應具備的一些理想特性。
理想特性
屬性 1 :每個位置的唯一編碼(跨序列)
每個位置都需要一個無論序列長度如何都保持一致的唯一編碼 - 無論當前序列的長度是 10 還是 10,000,位置 5 處的標記都應該具有相同的編碼。
屬性 2 :兩個編碼位置之間的線性關系
位置之間的關系在數學上應該是簡單的。如果知道位置 p 的編碼,那么計算位置 p+k 的編碼就應該很簡單,這樣模型就能更容易地學習位置模式。
如果你想一想如何在數線上表示數字,就不難理解 5 距離 3 是 2 步,或者 10 距離 15 是 5 步。同樣的直觀關系也應該存在于編碼中。
屬性 3:可泛化到比訓練中遇到的序列更長的序列上
為了提高模型在現實世界中的實用性,它們應該在訓練分布之外泛化。因此,編碼方案需要有足夠的適應性,以處理意想不到的輸入長度,同時又不違反任何其他理想特性。
屬性 4:由模型可以學習確定性過程生成
如果位置編碼能從一個確定的過程中產生,那將是最理想的。這樣,模型就能有效地學習編碼方案背后的機制。
屬性 5:可擴展至多個維度
隨著多模態模型成為常態,位置編碼方案必須能夠自然地從 1D 擴展到 nD。這將使模型能夠使用像圖像或腦部掃描這樣的數據,它們分別是 2D 和 4D 的。
現在我們知道了理想的屬性(以下簡稱為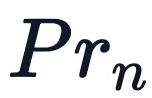 ),讓我們開始設計和迭代編碼方案吧。
),讓我們開始設計和迭代編碼方案吧。
整數位置編碼
我們首先想到的方法是將 token 位置的整數值添加到 token 嵌入的每個分量中,取值范圍為 0→L,其中 L 是當前序列的長度。
 IntegerEncoding
IntegerEncoding
在上面的動畫中,我們為索引中的 token 創建了位置編碼向量,并將其添加到 token 嵌入中。這里的嵌入值是 Llama 3.2 1B 中真實值的子集。可以觀察到,這些值都集中在 0 附近。這樣可以避免在訓練過程中出現梯度消失或爆炸的情況,因此,我們希望在整個模型中都能保持這種情況。
很明顯,目前的方法會帶來問題,位置值的大小遠遠超過了輸入的實際值。這意味著信噪比非常低,模型很難從位置信息中分離出語義信息。
有了這一新知識,一個自然的后續方法可能是將位置值歸一化為 1/N。這就將數值限制在 0 和 1 之間,但也帶來了另一個問題。如果我們選擇 N 為當前序列的長度,那么每個長度不同的序列的位置值就會完全不同,這就違反了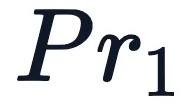 。
。
有沒有更好的方法來確保我們的數字介于 0 和 1 之間呢?如果我們認真思考一段時間,也許會想到將十進制數轉換為二進制數。
二進制位置編碼
我們可以將其轉換為二進制表示法,并將我們的值(可能已歸一化)與嵌入維度相匹配,而不是將我們的(可能已歸一化的)整數位置添加到嵌入的每個分量中,如下圖所示。
 BinaryEncoding
BinaryEncoding
我們將感興趣的位置(252)轉換為二進制表示(11111100),并將每一位添加到 token 嵌入的相應組件中。最小有效位(LSB)將在每個后續標記的 0 和 1 之間循環,而最大有效位(MSB)將每 2^(n-1) 個 token 循環一次,其中 n 是位數。你可以在下面的動畫中看到不同索引的位置編碼向量。
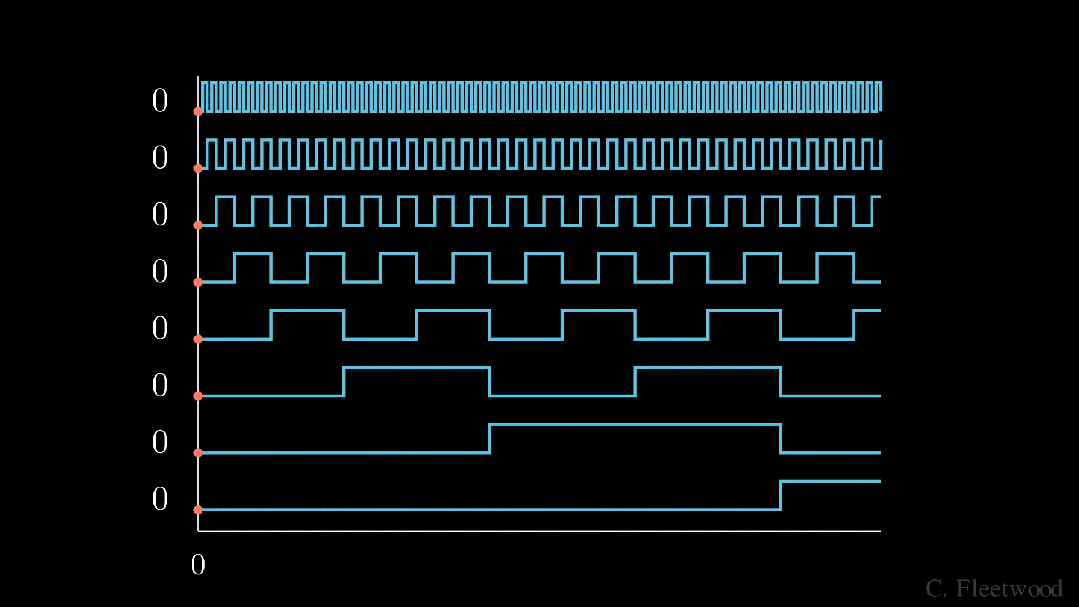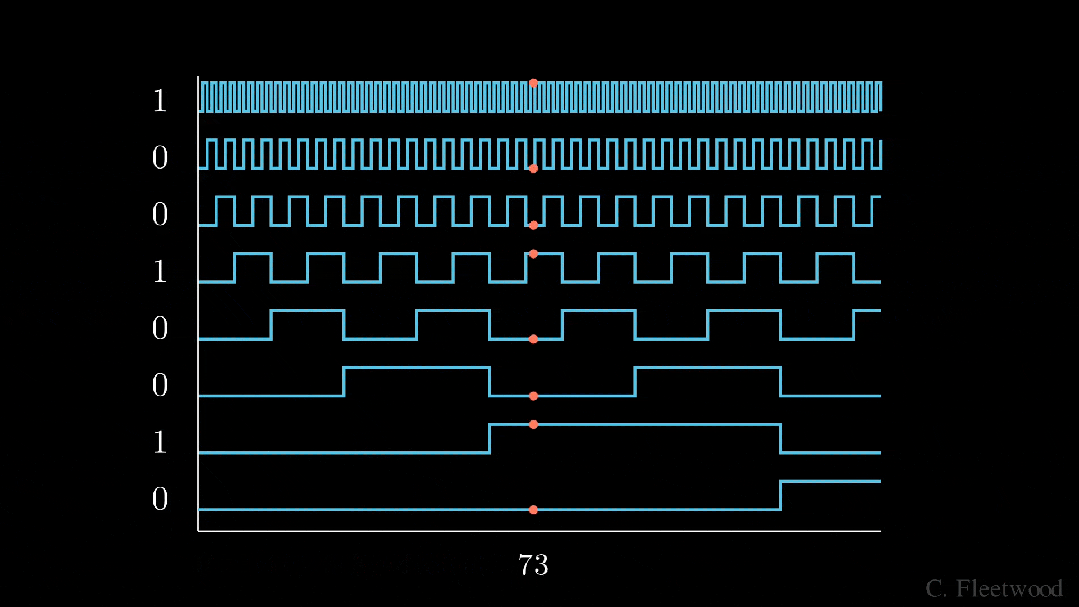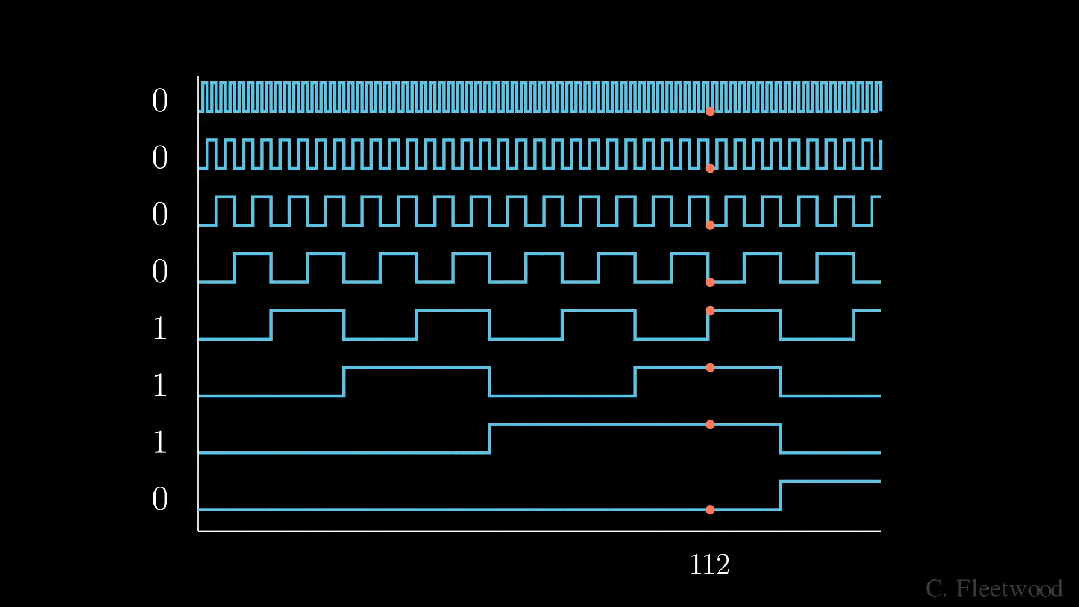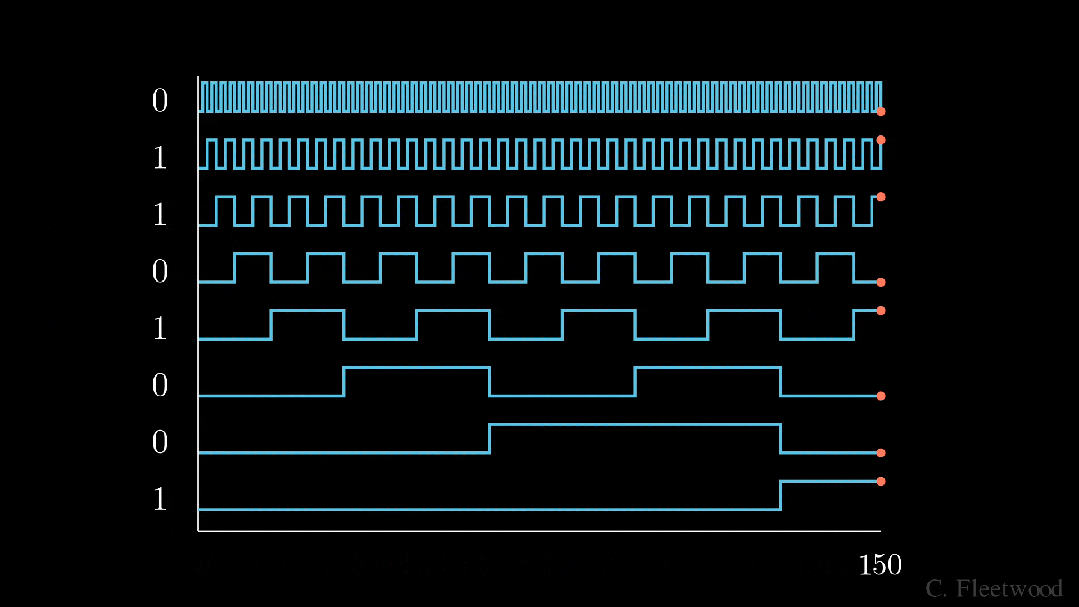
我們已經解決了數值范圍的問題,現在我們有了在不同序列長度上保持一致的唯一編碼。如果我們繪制 token 嵌入的低維版本,并可視化不同值的二進制位置向量的加法,會發生什么情況呢?
可以看到,結果非常「跳躍」(正如我們對二進制離散性的預期)。優化過程喜歡平滑、連續和可預測的變化。那么有哪些具有類似取值范圍的函數是平滑連續的嗎?
如果我們稍加留意,就會發現 sin 和 cos 都符合要求!
正弦位置編碼
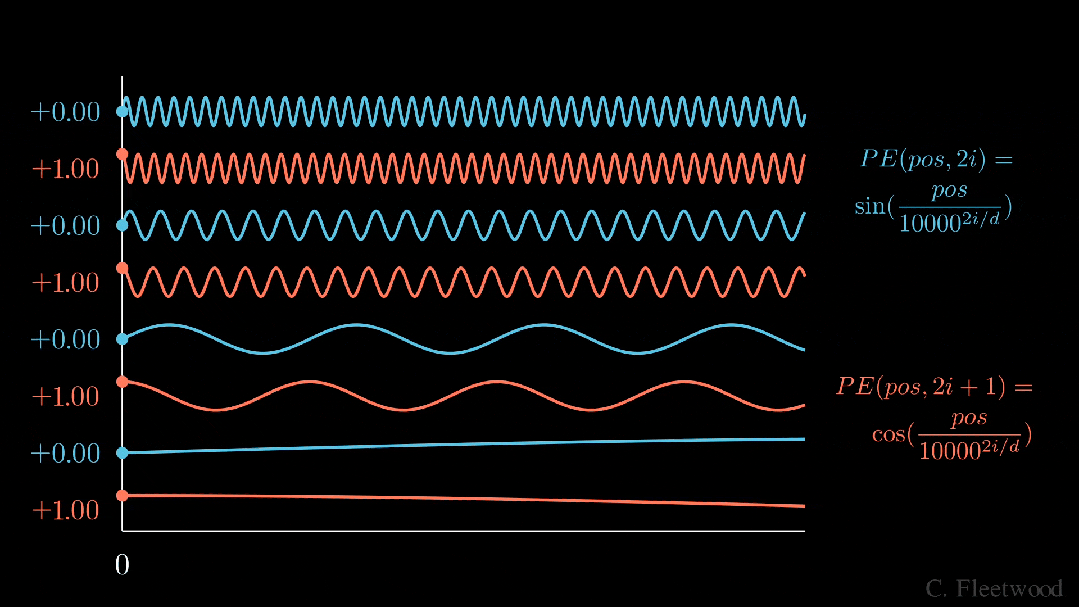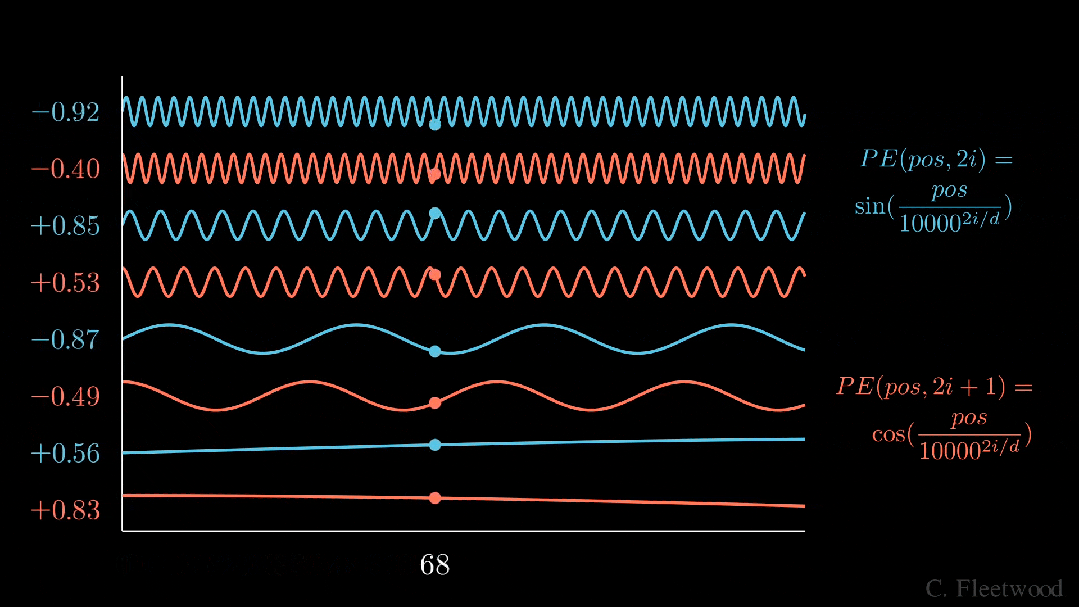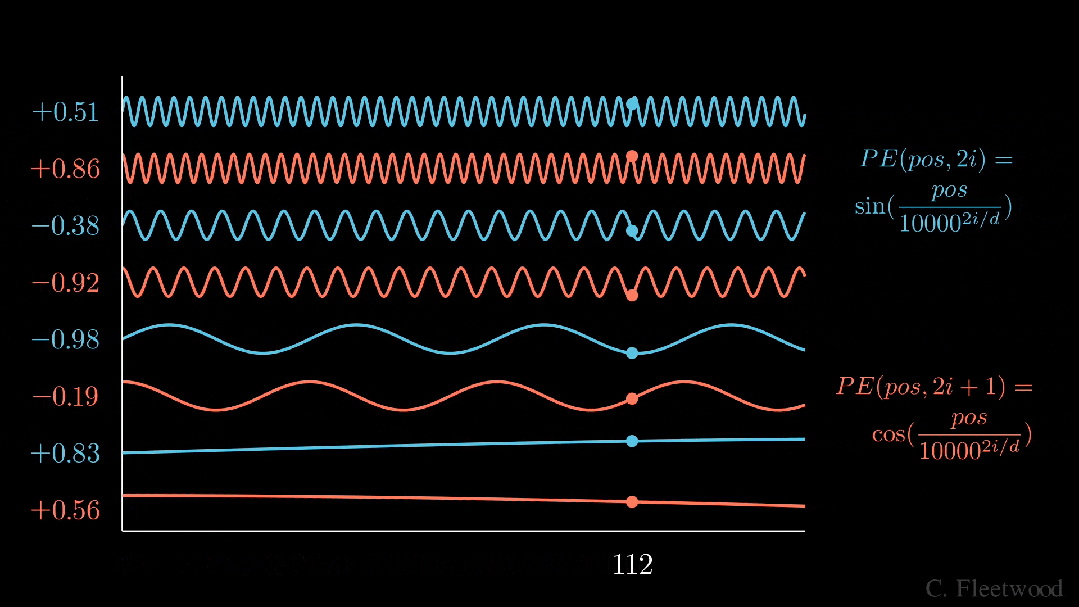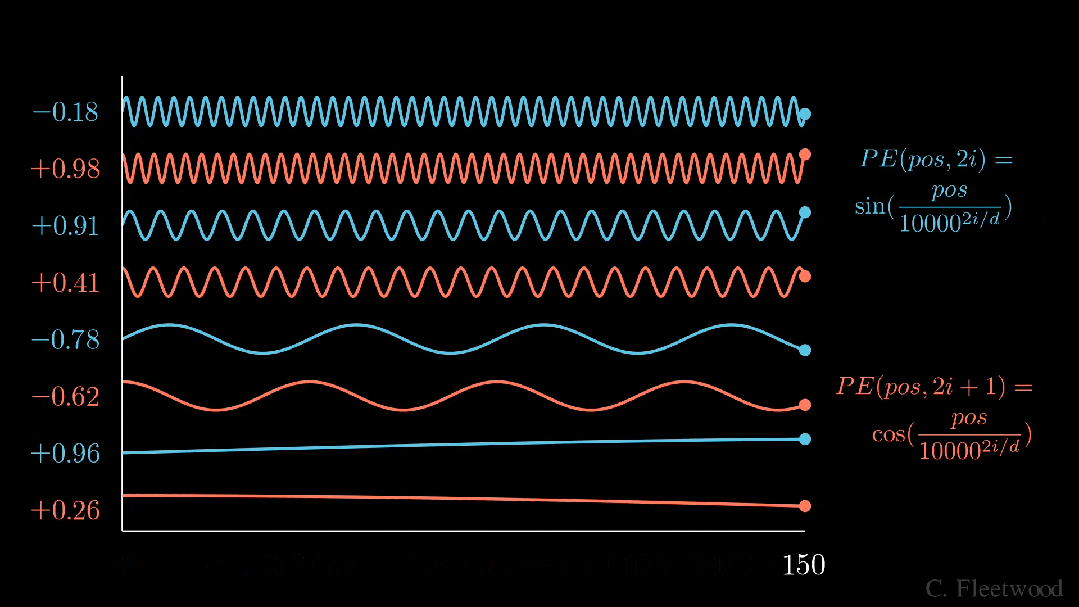
上面的動畫形象地展示了我們的位置嵌入,如果每個分量都是由波長逐漸增加的 sin 和 cos 交替繪制而成。如果將其與之前的動畫進行比較,你會發現兩者有驚人的相似之處。
現在,我們已經掌握了正弦波嵌入的方法,這最初是在《Attention is all you need》論文中定義的。讓我們來看看方程式:
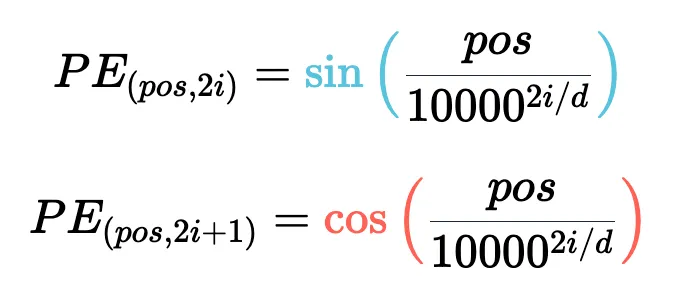
其中,pos 是詞塊位置索引,i 是位置編碼向量中的分量索引,d 是模型維度。10,000 是基本波長(下文簡稱為 θ),我們根據分量索引的函數對其進行拉伸或壓縮。我鼓勵大家輸入一些實際值來感受這種幾何級數。
這個等式有幾個部分乍看之下令人困惑。作者是如何選擇 10,00 的?為什么偶數和奇數位置分別使用 sin 和 cos?
看來,使用 10000 作為基本波長是通過實驗確定的。破解 sin 和 cos 的用法涉及的問題較多,但對我們的迭代理解方法至關重要。這里的關鍵是我們希望兩個編碼位置之間存在線性關系 ( )。要理解正弦和余弦如何配合使用才能產生這種線性關系,我們必須深入學習一些三角學知識。
)。要理解正弦和余弦如何配合使用才能產生這種線性關系,我們必須深入學習一些三角學知識。
考慮一串正弦和余弦對,每對都與頻率 ω_i 相關聯。我們的目標是找到一個線性變換矩陣 M,它能將這些正弦函數移動一個固定的偏移量 k:
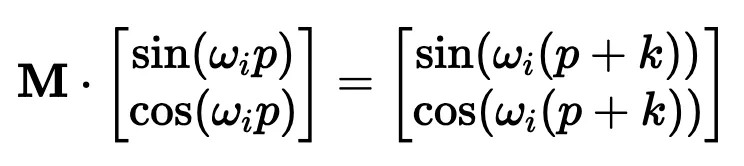
頻率 ω_i 隨維度指數 i 遞減,其幾何級數為:
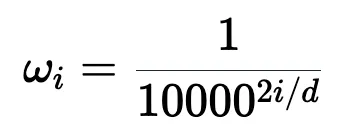
要找到這個變換矩陣,我們可以將其表示為一個包含未知系數 u_1、v_1、u_2 和 v_2 的一般 2×2 矩陣:
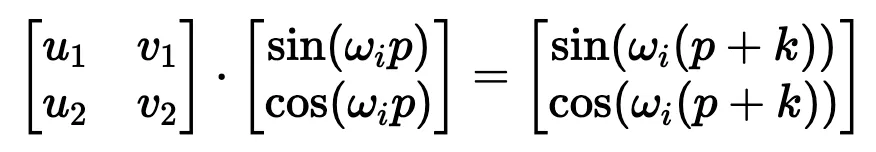
根據三角加法定理,我們可以將右邊的公式擴展為:
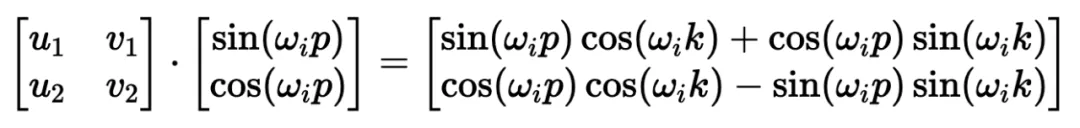
通過匹配系數,此展開式為我們提供了兩個方程的系統:
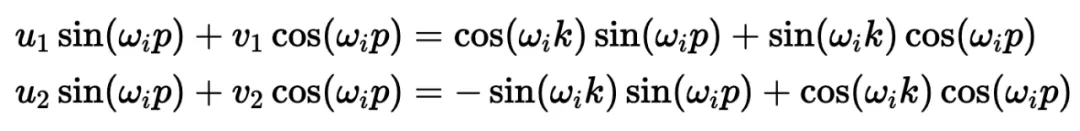
通過比較兩邊的 sin (ω_ip) 和 cos (ω_ip) 項,我們可以解出未知系數:
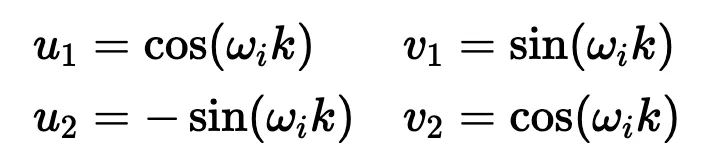
這些解決方案為我們提供了最終的變換矩陣 M_k:
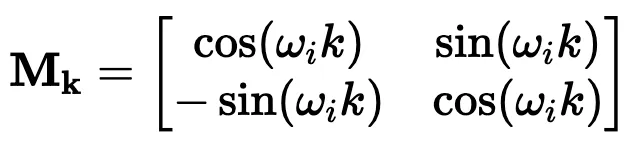
如果你以前做過游戲編程,你可能會發現我們的推導結果非常熟悉。沒錯,這就是旋轉矩陣。
因此,早在 2017 年,Noam Shazeer 在《Attention is all you need》論文中設計的編碼方案就已經將相對位置編碼為旋轉。從正弦編碼到 RoPE 又花了 4 年時間,盡管旋轉已經擺在桌面上......
絕對 vs 相對位置編碼
在了解了旋轉在這里的重要性之后,讓我們回到我們的激勵樣本,嘗試為下一次迭代發現一些直覺。

在上面,我們可以看到 token 的絕對位置,以及從 chased 到其他 token 的相對位置。通過正弦編碼,我們生成了一個單獨的向量來表示絕對位置,并使用一些三角函數技巧來編碼相對位置。
當我們試圖理解這些句子時,這個單詞是這篇博文的第 2149 個單詞重要嗎?還是我們關心它與周圍單詞的關系?一個單詞的絕對位置對其意義來說很少重要,重要的是單詞之間的關系。
上下文中的位置編碼
從這一點出發,在自注意力的背景下考慮位置編碼是關鍵。重申一下,自注意力機制使模型能夠衡量輸入序列中不同元素的重要性,并動態調整它們對輸出的影響。
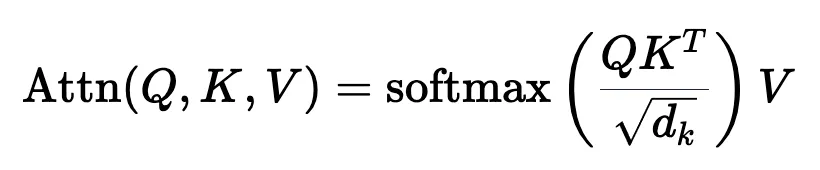
在我們以前的迭代中,我們已經生成了一個單獨的位置編碼向量,并在 Q、 K 和 V 投影之前將其添加到我們的 token 嵌入中。通過將位置信息直接添加到 token 嵌入中,我們正在用位置信息污染語義信息。我們應該嘗試在不修改規范的情況下對信息進行編碼。轉向乘法是關鍵。
使用字典類比,當查找一個詞 (查詢) 在我們的字典 (鍵) ,附近的詞應該比遙遠的詞有更多的影響。一個 token 對另一個 token 的影響是由 QK^T 點積決定的 —— 所以這正是我們應該關注位置編碼的地方。
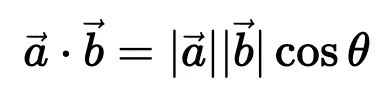
上面顯示的點乘的幾何解釋給了我們一個洞察:我們可以通過增加或減小兩個向量之間的夾角來調整我們的兩個向量的點積的結果。此外,通過旋轉向量,我們對向量的范數完全沒有影響,這個范數編碼了我們 token 的語義信息。
因此,現在我們知道注意力集中在哪里,并且從另一個角度看到了為什么旋轉可能是一個合理的「通道」,在其中編碼我們的位置信息,讓我們把它們放在一起。
旋轉位置編碼
RoForm 的論文中定義了旋轉位置編碼或 RoPE (蘇劍林在他的博客中獨立設計了它)。如果你直接跳到最終結果,這看起來像是巫術,通過在自注意力 (更具體地說是點積) 的背景下思考正弦編碼,我們可以看到它是如何整合在一起的。
就像在 Sinusoidal Encoding 一樣,我們把向量 (q 或 k,而不是預先投影 x) 分解成 2D 對 / 塊。我們沒有直接編碼絕對位置,而是加入一個我們從頻率緩慢遞減的正弦函數中提取的矢量,我們切入 chase,通過將每對旋轉矩陣相乘來編碼相對位置。
設 q 或 k 是位置為 p 的輸入向量。我們創建了一個塊對角矩陣,其中 M_i 是該組件對所需旋轉的對應旋轉矩陣:
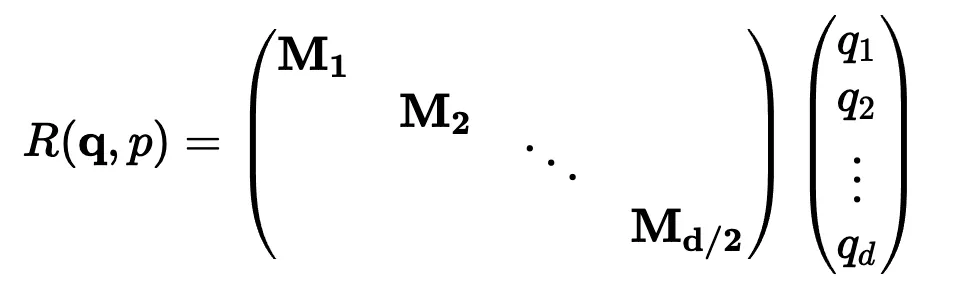
與正弦編碼非常相似,M_i 是簡單的:
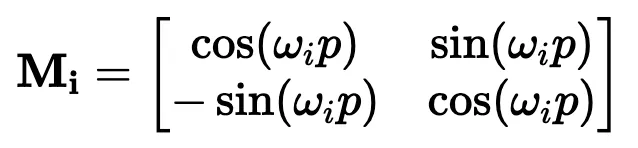

在實踐中,我們不使用矩陣乘法來計算 RoPE,因為使用這樣一個稀疏的矩陣會導致計算效率低下。相反,我們可以利用計算中的規則模式,將旋轉直接應用于獨立的元素對:
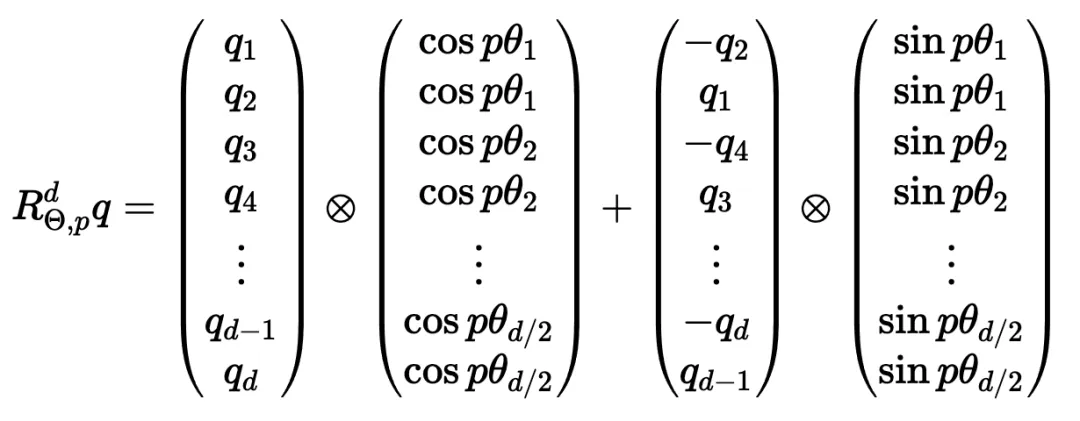
就是這樣!通過巧妙地將我們的旋轉應用于點積之前的 q 和 k 的 2D 塊,并從加法轉換為乘法,我們可以在評估中獲得很大的性能提升。
將 RoPE 擴展到 n 維
我們已經探討了 1D 情況下的 RoPE,這一點,我希望你已經獲得了一個直觀的理解,公認的非直觀組成部分的 transformer。最后,讓我們探索如何將其擴展到更高的維度,例如圖像。
第一直覺可能是直接使用圖像中的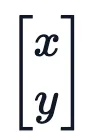 坐標對。這可能看起來很直觀,畢竟,我們之前幾乎是任意地對組件進行配對。然而,這會是一個錯誤!
坐標對。這可能看起來很直觀,畢竟,我們之前幾乎是任意地對組件進行配對。然而,這會是一個錯誤!
在 1D 情況下,我們通過從輸入向量旋轉一對值來編碼相對位置 m-n。對于 2D 數據,我們需要編碼水平和垂直的相對位置,比如 m-n 和 i-j 是獨立的。RoPE 的優勢在于它如何處理多個維度。我們沒有嘗試在一個旋轉中編碼所有位置信息,而是將同一維度內的組件配對并旋轉它們,否則我們將混合使用 x 和 y 偏移量信息。通過獨立處理每個維度,我們保持了空間的自然結構。這可以根據需要推廣到任意多個維度!
位置編碼的未來
RoPE 是位置編碼的最終化身嗎?DeepMind 最近的一篇論文(https://arxiv.org/pdf/2410.06205)深入分析了 RoPE,并強調了一些基本問題。
我預計未來會有一些突破,也許會從信號處理中獲得靈感,比如小波或者分層實現。隨著模型越來越多地被量化用于部署,我也希望在編碼方案中看到一些創新,這些編碼方案在低精度算術下仍然具有魯棒性。