原來機器學習那么簡單—SVR
一、算法介紹
支持向量回歸(SVR)是一種監督學習算法,用于解決回歸問題。其核心思想是找到一個超平面,這個超平面能夠以最小的誤差包含所有的訓練樣本。與支持向量機處理分類問題類似,支持向量回歸的目標是確保盡可能多的數據點位于由超平面決定的邊界內。
二、算法原理
2.1 基本思想
SVR的目標是找到一個函數 ,使得該函數在整個數據集上的偏差最小,并且同時保證模型的復雜度較低,以提高模型的泛化能力。在實現上,這通常通過引入所謂的“軟間隔”來實現,允許某些數據點可以處于誤差允許的范圍之外,從而達到更好的預測效果。
2.2 數學模型
在支持向量回歸中,我們試圖找到一個線性函數 ,其中 是權重向量, 是偏置。我們希望大部分的數據點 都滿足 ,這里的 是預先設定的一個小的非負數,表示容忍的誤差范圍。
為了找到這樣的函數,我們需要解決以下優化問題:
其中, 和 是松弛變量,用于處理不在誤差范圍內的數據點, 是正則化參數,用于控制模型復雜度和誤差之間的平衡。
2.3 核技巧
在實際應用中,很多問題的數據分布可能是非線性的,直接使用線性函數進行回歸可能無法達到較好的效果。SVR通過引入核函數來解決這一問題。核函數可以將數據映射到一個高維空間,在這個高維空間中,原本線性不可分的數據可能變得線性可分。常見的核函數包括線性核、多項式核、徑向基函數(RBF)核等。
三、案例分析
為了進一步理解支持向量回歸(SVR)的應用,我們將使用加州房價數據集進行模型訓練和測試。加州房價數據集包含以下特征:
- MedInc:收入中位數
- HouseAge:房屋年齡的中位數
- AveRooms:平均房間數目
- AveBedrms:平均臥室數目
- Population:區域人口
- AveOccup:平均入住率
- Latitude:緯度
- Longitude:經度
數據集的目標變量為MedHouseVal,即房屋價值的中位數(單位為$100,000)。
案例代碼
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# 加載數據
california = fetch_california_housing()
X = pd.DataFrame(california.data, columns=california.feature_names)
y = california.target
X
# 數據預處理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 創建SVR模型
svr = SVR(kernel='rbf')
# 訓練模型
svr.fit(X_train, y_train)
# 預測測試集
y_pred = svr.predict(X_test)
# 計算MSE
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')
# 可視化實際值與預測值
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r--', lw=2)
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs. Predicted')
plt.show()
# 可視化誤差分布
errors = y_pred - y_test
plt.figure(figsize=(10, 6))
plt.hist(errors, bins=20, color='purple')
plt.xlabel('Prediction Error')
plt.ylabel('Frequency')
plt.title('Prediction Error Distribution')
plt.show()四、結果分析
通過運行代碼,得到模型在測試集上的平均平方誤差(MSE)為:0.3551984619989417。這個值越低,表示模型的預測能力越好。大家可以通過更換 SVR 的核函數類型(如 'linear', 'poly' 等)來嘗試改善模型的表現。
預測值與實際值的對比圖如下:
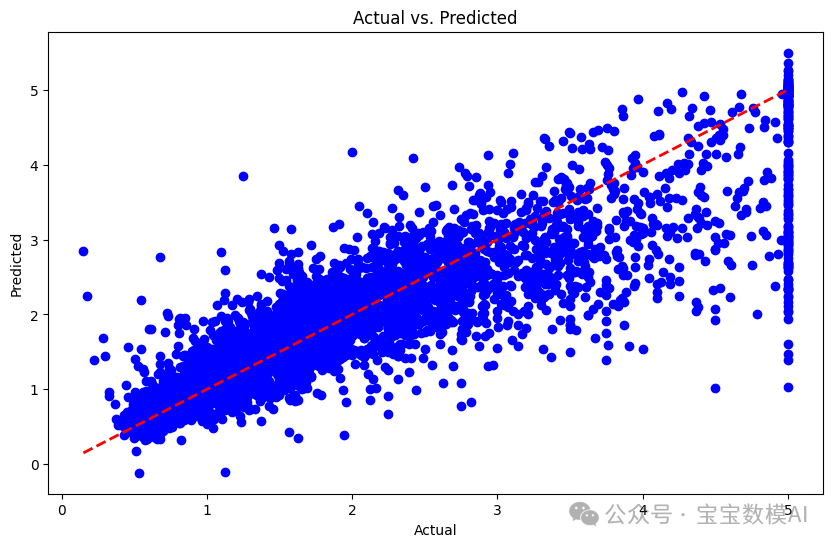 圖片
圖片
誤差分布圖如下:
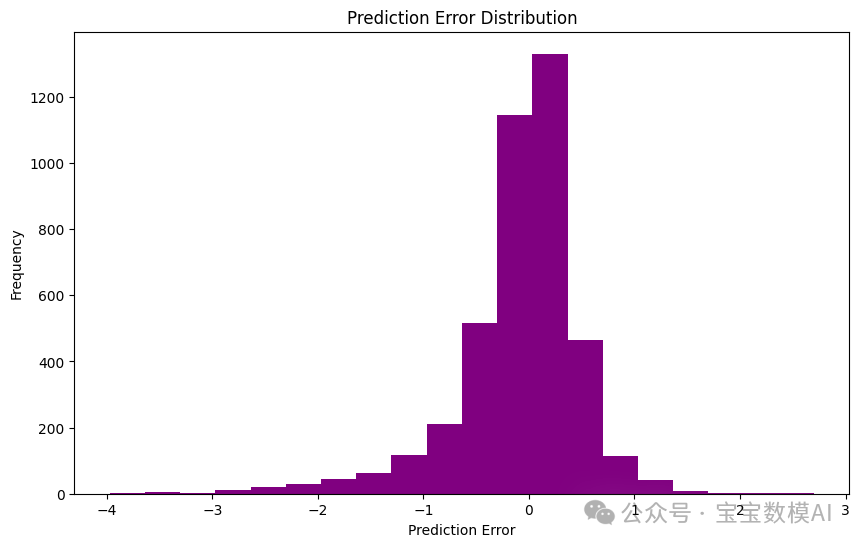 圖片
圖片
五、結論
通過這個案例,我們可以看到支持向量回歸在實際數據集上的應用。盡管 SVR 是一種強大的回歸工具,但選擇合適的核函數和調整模型參數對于獲得最佳性能至關重要。