使用機器學習技術進行時間序列缺失數據填充:基礎方法與入門案例
在時間序列分析領域中,數據缺失是一個不可避免的挑戰。無論是由于傳感器故障、數據傳輸中斷還是設備維護等原因,這些缺失都會對數據分析和預測造成顯著影響。傳統的處理方法,如前向填充或簡單插值,雖然實現簡單,但在處理復雜數據時往往表現不足。

具體來說,當時間序列具有以下特征時,傳統方法的局限性就會顯現:
- 存在復雜的非線性模式
- 包含多層次的趨勢變化
- 數據波動性較大
本文將通過實際案例,詳細探討如何運用機器學習技術來解決時間序列的缺失值問題。
數據說明
為了確保研究的可重復性,我們構建了一個模擬的能源生產數據集。這個數據集具有以下特征:
- 時間范圍:2023年1月1日至2023年3月1日
- 采樣頻率:10分鐘
- 數據特點:包含真實的晝夜能源生產周期
- 缺失設置:隨機選擇10%的數據點作為缺失值
讓我們首先看看如何生成這個數據集:
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
# 生成模擬能源生產數據
start_date = datetime(2023, 1, 1)
end_date = datetime(2023, 3, 1)
datetime_index = pd.date_range(start=start_date, end=end_date, freq='10T')
# 創建具有晝夜周期的能源生產值
np.random.seed(42) # 設置隨機種子以確保可重復性
base_energy = []
for dt in datetime_index:
hour = dt.hour
if 6 <= hour <= 18: # 白天時段:較高的能源生產
energy = np.random.normal(loc=300, scale=30)
else: # 夜間時段:較低的能源生產
energy = np.random.normal(loc=50, scale=15)
base_energy.append(energy)
energy_production = pd.Series(base_energy)
# 隨機引入缺失值
num_missing = int(0.1 * len(energy_production))
missing_indices = np.random.choice(len(energy_production), num_missing, replace=False)
energy_production.iloc[missing_indices] = np.nan
# 創建數據框架
mock_energy_data_with_missing = pd.DataFrame({
'Datetime': datetime_index,
'Energy_Production': energy_production
})
# 添加時間索引便于后續分析
data_with_index = mock_energy_data_with_missing.reset_index()
data_with_index['Time_Index'] = np.arange(len(data_with_index))
# 數據可視化
plt.figure(figsize=(14, 7))
plt.plot(mock_energy_data_with_missing['Datetime'],
mock_energy_data_with_missing['Energy_Production'],
label='Energy Production (With Missing)', color='blue', alpha=0.7)
plt.scatter(mock_energy_data_with_missing['Datetime'],
mock_energy_data_with_missing['Energy_Production'],
c=mock_energy_data_with_missing['Energy_Production'].isna(),
cmap='coolwarm',
label='Missing Values', s=10)
plt.title('模擬能源生產數據集(10分鐘間隔采樣)')
plt.xlabel('時間')
plt.ylabel('能源生產量')
plt.legend(['能源生產(含缺失值)', '缺失值'])
plt.grid(True)
plt.show()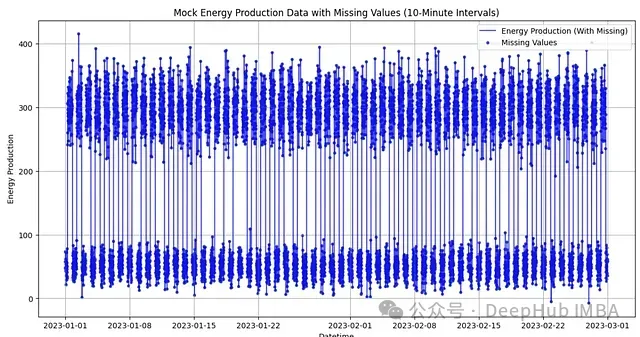 圖1:模擬能源生產數據可視化。藍線表示能源生產數據,散點表示缺失值的位置
圖1:模擬能源生產數據可視化。藍線表示能源生產數據,散點表示缺失值的位置
從上圖中,我們可以清晰地觀察到以下特征:
- 數據展現出明顯的周期性波動,這反映了能源生產的晝夜變化規律
- 缺失值(散點標記)隨機分布在整個時間序列中
- 能源生產量在白天和夜間有顯著的水平差異
這個數據集為我們研究不同補充方法的效果提供了理想的測試基礎。在接下來的分析中,我們將詳細探討如何運用機器學習方法來補充這些缺失值。
機器學習在時間序列補充中的應用基礎
機器學習方法的優勢
在時間序列數據分析中,機器學習方法相比傳統補充方法具有獨特優勢。傳統方法通常基于簡單的統計假設,而機器學習方法則能夠自適應地學習數據中的復雜模式和多維依賴關系。
非線性關系處理:在能源生產等實際場景中,變量之間往往存在復雜的非線性關系。機器學習模型能夠自動捕捉這些非線性模式,而無需預先指定關系形式。
多維特征利用:當數據集包含多個相關變量時,機器學習模型可以同時考慮多個特征的影響,從而提供更準確的估計。
大規模缺失處理:對于連續時間段的缺失,機器學習可以通過學習數據的長期模式來提供更可靠的補充值。
異常模式識別:在處理非隨機缺失時,機器學習方法表現出較強的魯棒性,能夠識別并適應異常模式。
線性回歸補充方法實現
我們首先探討線性回歸這一基礎但高效的補充方法。以下是詳細的實現步驟:
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 第一步:數據預處理
# 將時間索引作為特征,能源生產量作為目標變量
features = data_with_index[['Time_Index']]
target = data_with_index['Energy_Production']
# 第二步:分離完整數據和缺失數據
non_missing_data = data_with_index.dropna(subset=['Energy_Production'])
missing_data = data_with_index[data_with_index['Energy_Production'].isna()]
# 第三步:模型訓練
# 使用完整數據訓練線性回歸模型
regressor = LinearRegression()
regressor.fit(non_missing_data[['Time_Index']], non_missing_data['Energy_Production'])
# 第四步:缺失值預測
predicted_values = regressor.predict(missing_data[['Time_Index']])
# 第五步:將預測值填充到原始數據集
filled_data = data_with_index.copy()
filled_data.loc[filled_data['Energy_Production'].isna(), 'Energy_Production'] = predicted_values
filled_data = filled_data[['Datetime', 'Energy_Production']]
# 第六步:結果可視化(展示2023年1月數據)
start_month = datetime(2023, 1, 1)
end_month = datetime(2023, 1, 31)
original_month_data = mock_energy_data_with_missing[
(mock_energy_data_with_missing['Datetime'] >= start_month) &
(mock_energy_data_with_missing['Datetime'] <= end_month)
]
imputed_month_data = filled_data[
(filled_data['Datetime'] >= start_month) &
(filled_data['Datetime'] <= end_month)
]
plt.figure(figsize=(14, 7))
plt.plot(imputed_month_data['Datetime'], imputed_month_data['Energy_Production'],
label='補充后數據', color='green', alpha=0.8)
plt.plot(original_month_data['Datetime'], original_month_data['Energy_Production'],
label='原始數據(含缺失)', color='red', alpha=0.9)
plt.title('原始數據與線性回歸補充數據對比(2023年1月)')
plt.xlabel('時間')
plt.ylabel('能源生產量')
plt.legend()
plt.grid(True)
plt.show()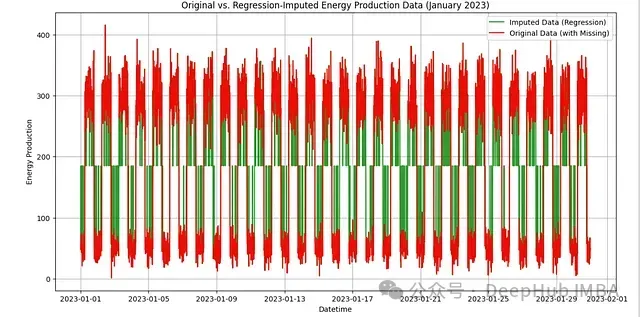 圖2:線性回歸補充效果可視化。綠線表示補充后的數據,紅線表示原始數據
圖2:線性回歸補充效果可視化。綠線表示補充后的數據,紅線表示原始數據
補充效果的多維度評估
為了全面評估補充效果,我們需要從多個維度進行分析。以下是詳細的評估框架:
from statsmodels.tsa.seasonal import seasonal_decompose
# 統計特征分析
original_stats = mock_energy_data_with_missing['Energy_Production'].describe()
imputed_stats = filled_data['Energy_Production'].describe()
# 創建比較表
stats_comparison = pd.DataFrame({
'Metric': original_stats.index,
'Original Data': original_stats.values,
'Imputed Data (Linear Regression)': imputed_stats.values
})
# 輸出統計比較結果
print("數據統計特征對比:")
print(stats_comparison)這個統計分析揭示了以下關鍵發現:
- 數據完整性:補充后的數據集從7648個觀測值增加到8497個,實現了完整覆蓋。
- 中心趨勢:補充后數據的均值(185.07)與原始數據基本一致,表明保持了數據的整體水平。
- 離散程度:補充數據的標準差(120.31)略低于原始數據(126.82),表明發生了一定程度的平滑。
- 分布特征:雖然最大值和最小值保持不變,但中位數的變化反映出分布形態有所改變。
通過這些初步分析,我們可以看到線性回歸方法在保持數據基本特征方面表現良好,但也存在一定的局限性,特別是在處理數據的變異性方面。在下一部分中,我們將進一步探討更多高級評估指標,以及決策樹回歸等其他補充方法的表現。
時間序列補充效果的深入評估
在時間序列分析中,僅依靠基本的統計指標是不夠的。我們需要特別關注數據的時序特性,包括自相關性、趨勢和季節性模式。讓我們逐步深入這些關鍵評估維度。
自相關性分析
自相關性反映了時間序列中相鄰觀測值之間的依賴關系。保持適當的自相關結構對于確保補充數據的時序特性至關重要。以下是詳細的分析過程:
import statsmodels.api as sm
def plot_acf_comparison(original_series, imputed_series, lags=50):
"""
繪制并比較原始數據和補充數據的自相關函數
參數:
original_series: 原始時間序列
imputed_series: 補充后的時間序列
lags: 滯后階數
"""
plt.figure(figsize=(14, 5))
# 分析原始數據的自相關性
plt.subplot(1, 2, 1)
sm.graphics.tsa.plot_acf(original_series.dropna(), lags=lags,
ax=plt.gca(), title="原始數據的自相關函數")
plt.grid(True)
# 分析補充數據的自相關性
plt.subplot(1, 2, 2)
sm.graphics.tsa.plot_acf(imputed_series, lags=lags,
ax=plt.gca(), title="補充數據的自相關函數")
plt.grid(True)
plt.tight_layout()
plt.show()
# 執行自相關分析
plot_acf_comparison(mock_energy_data_with_missing['Energy_Production'],
filled_data['Energy_Production'])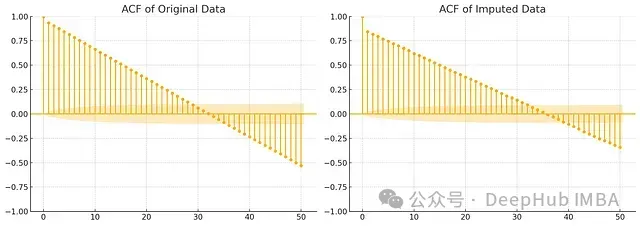 圖3:自相關函數對比分析。左圖顯示原始數據的自相關性,右圖顯示補充后數據的自相關性
圖3:自相關函數對比分析。左圖顯示原始數據的自相關性,右圖顯示補充后數據的自相關性
從自相關分析中,我們可以觀察到幾個重要特征:
- 短期相關性:補充數據在短期滯后期(1-5個lag)的自相關系數與原始數據非常接近,表明短期時間依賴關系得到了良好保持。
- 周期性特征:兩個圖中都清晰顯示出規律的波動模式,這反映了數據中的日周期特性被很好地保留。
- 相關強度:補充數據的自相關系數整體略低于原始數據,這是線性回歸補充過程中不可避免的平滑效應導致的。
時間序列分解分析
為了更深入地理解補充效果,我們使用STL(Seasonal-Trend decomposition using Loess)方法將時間序列分解為趨勢、季節性和殘差組件:
# 執行STL分解
original_series = mock_energy_data_with_missing['Energy_Production']
imputed_series = filled_data['Energy_Production']
# 考慮每日144個觀測值的周期(10分鐘采樣間隔)
original_decompose = seasonal_decompose(original_series.interpolate(),
model='additive', period=144)
imputed_decompose = seasonal_decompose(imputed_series.interpolate(),
model='additive', period=144)
# 繪制趨勢比較
plt.figure(figsize=(14, 5))
plt.plot(original_decompose.trend, label='原始趨勢', color='blue')
plt.plot(imputed_decompose.trend, label='補充數據趨勢',
color='green', linestyle='--')
plt.title('趨勢組件比較:原始數據 vs 線性回歸補充')
plt.legend()
plt.grid(True)
plt.show()
# 繪制季節性比較
plt.figure(figsize=(14, 5))
plt.plot(original_decompose.seasonal, label='原始季節性', color='blue')
plt.plot(imputed_decompose.seasonal, label='補充數據季節性',
color='green', linestyle='--')
plt.xlim(0, 4000)
plt.title('季節性組件比較:原始數據 vs 線性回歸補充')
plt.legend()
plt.grid(True)
plt.show()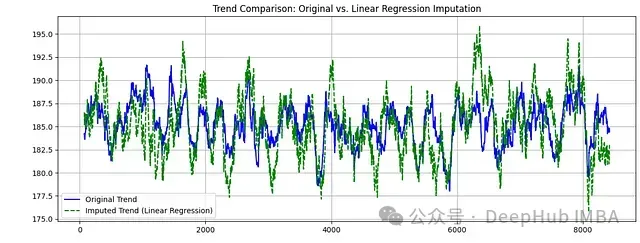 圖4:趨勢組件比較。藍線表示原始數據趨勢,綠虛線表示補充數據趨勢
圖4:趨勢組件比較。藍線表示原始數據趨勢,綠虛線表示補充數據趨勢
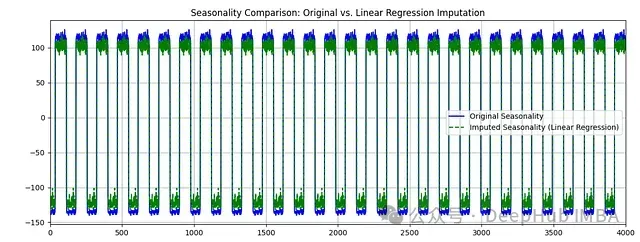 圖5:季節性組件比較。展示了原始數據和補充數據的周期性模式。
圖5:季節性組件比較。展示了原始數據和補充數據的周期性模式。
通過分解分析我們發現:
趨勢組件特征:
- 補充數據很好地保持了原始數據的長期趨勢方向
- 趨勢線的平滑程度增加,這是線性回歸方法的特性導致的
- 關鍵的趨勢轉折點得到了準確保持
季節性組件特征:
- 日內周期的基本模式被準確捕獲
- 補充數據的季節性振幅略有減小,表明極值被部分平滑
- 周期性的時間點(如日出、日落時段)的變化模式得到保持
這些分析結果提示我們,雖然線性回歸方法在保持數據的基本時序特性方面表現不錯,但在處理極值和突變點方面可能存在局限,所以我們選用一些更好的模型如決策樹回歸器,來改善這些方面的表現。
決策樹回歸方法的應用與評估
在觀察到線性回歸方法的局限性后,我們引入決策樹回歸器作為一種更靈活的補充方法。決策樹的非線性特性使其能夠更好地捕捉數據中的復雜模式。
決策樹回歸器的實現
讓我們首先看看如何使用決策樹進行缺失值補充:
from sklearn.tree import DecisionTreeRegressor
# 配置并訓練決策樹模型
# max_depth=5用于防止過擬合,同時保持足夠的模型復雜度
tree_regressor = DecisionTreeRegressor(max_depth=5, random_state=42)
tree_regressor.fit(non_missing_data[['Time_Index']],
non_missing_data['Energy_Production'])
# 使用訓練好的模型預測缺失值
tree_predicted_values = tree_regressor.predict(missing_data[['Time_Index']])
# 將預測值填充到原始數據集
tree_filled_data = data_with_index.copy()
tree_filled_data.loc[tree_filled_data['Energy_Production'].isna(),
'Energy_Production'] = tree_predicted_values
tree_filled_data = tree_filled_data[['Datetime', 'Energy_Production']]
# 可視化決策樹補充結果
plt.figure(figsize=(14, 7))
plt.plot(tree_imputed_month_data['Datetime'],
tree_imputed_month_data['Energy_Production'],
label='決策樹補充數據', color='orange', alpha=0.8)
plt.plot(original_month_data['Datetime'],
original_month_data['Energy_Production'],
label='原始數據(含缺失)', color='red', alpha=0.9)
plt.title('原始數據與決策樹補充數據對比(2023年1月)')
plt.xlabel('時間')
plt.ylabel('能源生產量')
plt.legend()
plt.grid(True)
plt.show()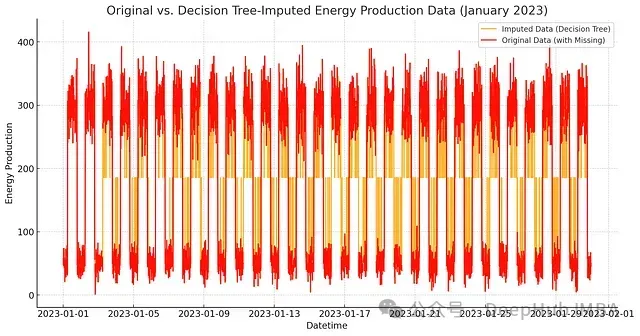 圖6:決策樹補充結果可視化。橙線表示決策樹補充的數據,紅線表示原始數據
圖6:決策樹補充結果可視化。橙線表示決策樹補充的數據,紅線表示原始數據
從圖中可以直觀地看到,決策樹方法在保持數據特征方面展現出了以下優勢:
- 更好地保持了數據的局部變化特征
- 對極值的處理更為準確
- 補充結果展現出更自然的波動性
補充效果對比分析
讓我們通過各項指標來系統比較兩種方法的表現:
# 統計指標比較
stats_comparison['決策樹補充數據'] = tree_filled_data['Energy_Production'].describe()核心統計指標對比:
Metric Original Data Linear Regression Decision Tree
count 7648.000000 8497.000000 8497.000000
mean 185.073509 185.073842 184.979184
std 126.816229 120.313162 120.633636
min -7.549833 -7.549833 -7.549833
25% 51.793304 54.186258 53.797479
50% 256.996772 185.197681 185.545605
75% 302.217789 298.324435 298.531049
max 415.581945 415.581945 415.581945這些數據揭示了一些重要的發現:
分布特征保持:
- 決策樹補充的數據在標準差方面(120.63)比線性回歸(120.31)更接近原始數據(126.82)
- 兩種方法都很好地保持了數據的整體范圍(最小值和最大值)
- 決策樹在四分位數的保持上表現更好,特別是在中位數方面
自相關性分析:
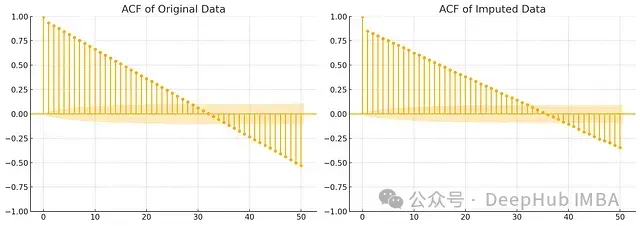 圖7:兩種方法的自相關分析對比
圖7:兩種方法的自相關分析對比
決策樹方法在時間依賴性的保持方面表現出明顯優勢:
- 更準確地保持了短期相關性強度
- 更好地捕捉了周期性模式
- 自相關結構的衰減特征更接近原始數據
- 趨勢和季節性分解:
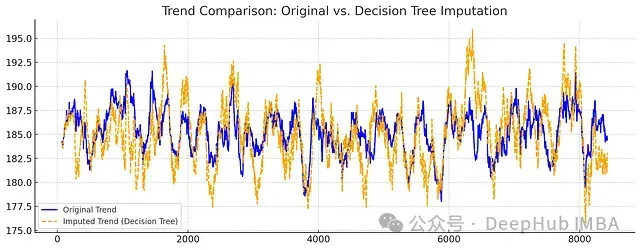 圖8:趨勢組件比較
圖8:趨勢組件比較
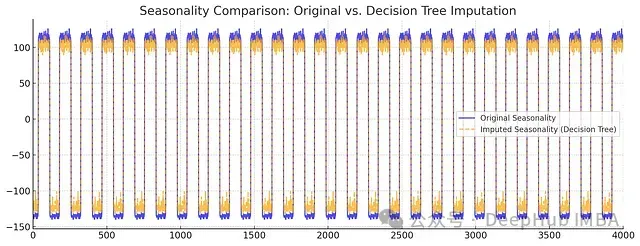 圖9:季節性組件比較
圖9:季節性組件比較
從分解結果可以看出:
- 決策樹方法在保持趨勢的細節特征方面表現更好
- 季節性模式的振幅和相位都得到了更準確的保持
- 整體而言,決策樹補充的數據展現出更自然的時間序列特性
方法優劣勢總結與應用建議
基于以上分析,我們可以得出以下結論:
線性回歸方法的特點:
- 優勢:計算效率高,實現簡單
- 劣勢:對非線性模式的捕捉能力有限
- 適用場景:數據呈現明顯的線性趨勢,且波動較為規律
決策樹方法的特點:
- 優勢:能更好地處理非線性關系,保持數據的局部特征
- 劣勢:計算復雜度較高,需要更多的參數調優
- 適用場景:數據具有復雜的非線性模式,需要保持精細的局部特征
實踐建議:
- 對于簡單的時間序列,可以優先考慮線性回歸方法
- 在處理復雜模式的數據時,建議使用決策樹方法
- 可以根據具體應用場景的需求(如計算資源限制、精度要求等)來選擇合適的方法
本文展示了機器學習方法在時間序列缺失值補充中的有效性,并提供了方法選擇的實踐指導。這些方法和評估框架可以推廣到其他類似的時間序列分析場景中。







































