本文種展示的特征傳播是一種用于處理圖機(jī)器學(xué)習(xí)應(yīng)用程序中缺失的特征的有效且可擴(kuò)展的方法。它很簡(jiǎn)單，但效果出奇地好。

圖神經(jīng)網(wǎng)絡(luò) (GNN) 模型通常假設(shè)每個(gè)節(jié)點(diǎn)都有一個(gè)完整的特征向量。以一個(gè) 2 層 GCN 模型 [1] 為例，它具有以下形式：

Z = A σ(AXW?) W?

該模型的兩個(gè)輸入是編碼圖結(jié)構(gòu)(歸一化的)鄰接矩陣 A 和作為行的節(jié)點(diǎn)特征的特征矩陣 X，輸出為節(jié)點(diǎn)嵌入 Z。GCN 的每一層執(zhí)行節(jié)點(diǎn)特征變換(參數(shù)化可學(xué)習(xí)矩陣 W? 和 W?)，然后將轉(zhuǎn)換后的特征向量傳播到相鄰節(jié)點(diǎn)。這里面一個(gè)重要的概念是：GCN 假設(shè) X 中的所有條目都被觀察到。

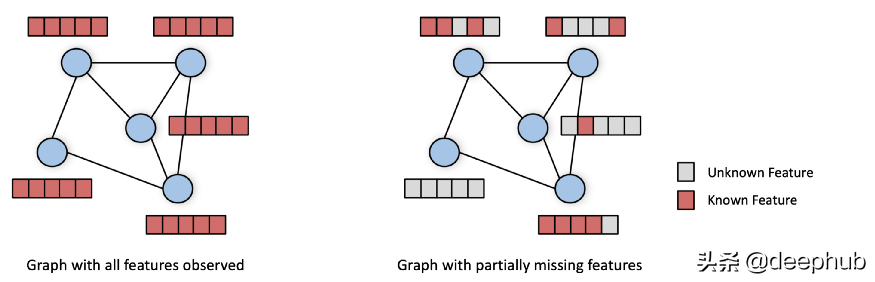
但是在現(xiàn)實(shí)世界的場(chǎng)景中，經(jīng)常會(huì)看到一些節(jié)點(diǎn)特征可能會(huì)缺失。例如，年齡、性別等人口統(tǒng)計(jì)信息可能僅對(duì)一小部分社交網(wǎng)絡(luò)用戶可用，而內(nèi)容特征通常僅對(duì)最活躍的用戶呈現(xiàn)。例如在推薦系統(tǒng)中并非所有產(chǎn)品都有與之相關(guān)的完整描述，這使得情況變得更加嚴(yán)重，隨著人們對(duì)數(shù)字隱私的認(rèn)識(shí)不斷提高，越來越多的數(shù)據(jù)只有在用戶明確同意的情況下才能獲得。

根據(jù)上面的描述，特征矩陣都有缺失值的，大多數(shù)現(xiàn)有的 GNN 模型都不能直接應(yīng)用。最近的幾項(xiàng)工作派生了能夠處理缺失特征的 GNN 模型(例如 [2-3])，但是這些模型在缺失特征率很高(>90%)的情況下受到影響，并且不能擴(kuò)展到具有超過幾百萬條邊的圖.

在 Maria Gorinova、Ben Chamberlain (Twitter)、Henry Kenlay 和 Xiaowen Dong (Oxford) 合著的一篇新論文 [4] 中，提出了特征傳播 (FP) [4] 作為一種簡(jiǎn)單但高效且令人驚訝的有效解決方案。 簡(jiǎn)而言之，F(xiàn)P 通過在圖上傳播已知特征來重構(gòu)缺失的特征。 然后可以將重建的特征輸入任何 GNN 以解決下游任務(wù)，例如節(jié)點(diǎn)分類或鏈接預(yù)測(cè)。

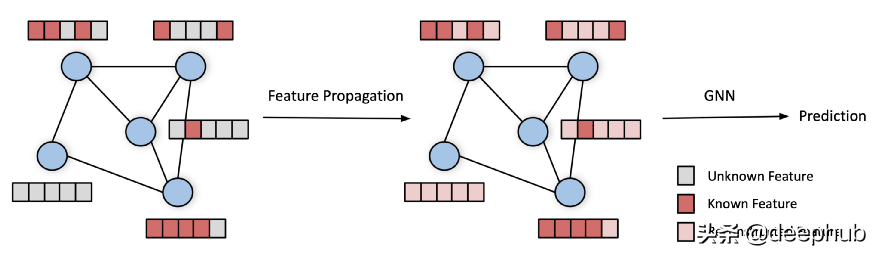
特征傳播框架。 輸入是缺少節(jié)點(diǎn)特征的圖(左)。 在初始步驟中，特征傳播通過迭代地?cái)U(kuò)散圖中的已知特征來重構(gòu)缺失的特征(中)。 隨后，圖和重建的節(jié)點(diǎn)特征被輸入到下游 GNN 模型中，然后產(chǎn)生預(yù)測(cè)(右)。

傳播步驟非常簡(jiǎn)單：首先，未知特征用任意值初始化[5]。 通過應(yīng)用(歸一化的)鄰接矩陣來傳播特征，然后將已知特征重置為其真實(shí)值。 我們重復(fù)這兩個(gè)操作，直到特征向量收斂[6]。

特征傳播是一種簡(jiǎn)單且令人驚訝的強(qiáng)大方法，用于在缺少特征的圖上進(jìn)行學(xué)習(xí)。 特征的每個(gè)坐標(biāo)都被單獨(dú)處理(x 表示 X 的一列)。

FP 可以從數(shù)據(jù)同質(zhì)性(“平滑性”)的假設(shè)中推導(dǎo)出來，即鄰居往往具有相似的特征向量。 同質(zhì)性的水平可以使用Dirichlet energy來量化，這是一種測(cè)量節(jié)點(diǎn)特征與其鄰居平均值之間的平方差的二次形式。 Dirichlet energy[7] 的梯度流是圖熱擴(kuò)散方程，以已知特征作為邊界條件。 FP 是使用具有單位步長(zhǎng)的顯式前向 Euler 方案作為該擴(kuò)散方程的離散化獲得的 [8]。

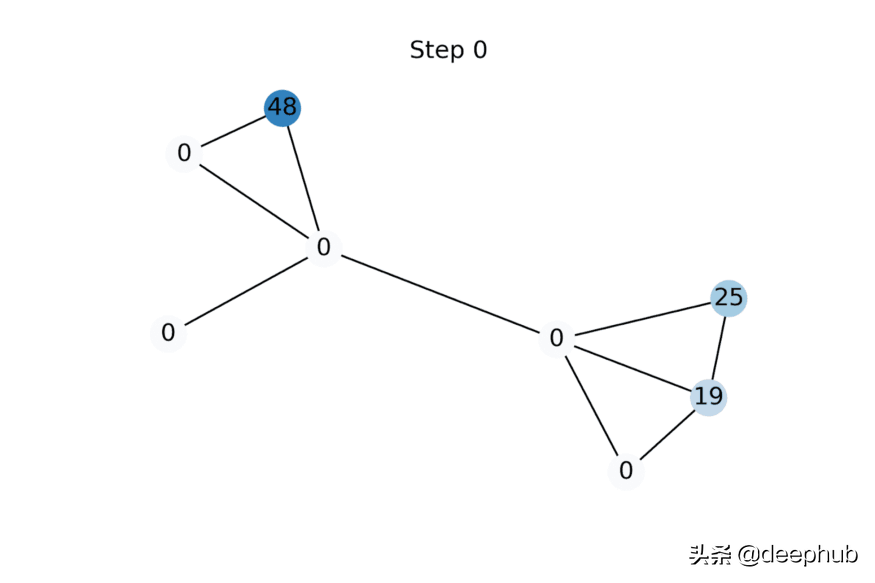
動(dòng)畫展示了隨著特征傳播的更多迭代應(yīng)用而標(biāo)量節(jié)點(diǎn)特征的演變示例。 未知特征被初始化為零，但很快收斂到使給定圖上的Dirichlet energy最小化的值。

特征傳播與標(biāo)簽傳播(LP)[9]相似。 關(guān)鍵區(qū)別在于 LP 是一種與特征無關(guān)的方法，它通過在圖中傳播已知標(biāo)簽來直接預(yù)測(cè)每個(gè)節(jié)點(diǎn)的類，而FP 用于首先重建缺失的節(jié)點(diǎn)特征，然后將其饋送到下游 GNN。 這使得 FP 能夠利用觀察到的特征，并在所有基準(zhǔn)測(cè)試中都優(yōu)于 LP。 在實(shí)踐中經(jīng)常發(fā)生帶標(biāo)簽的節(jié)點(diǎn)集和具有特征的節(jié)點(diǎn)集不一定完全重疊，因此這兩種方法并不總是可以直接比較。

論文中使用七個(gè)標(biāo)準(zhǔn)節(jié)點(diǎn)分類基準(zhǔn)對(duì) FP 進(jìn)行了廣泛的實(shí)驗(yàn)驗(yàn)證，其中隨機(jī)刪除了可變部分的節(jié)點(diǎn)特征(獨(dú)立于每個(gè)通道)。 FP 后跟一個(gè) 2 層 GCN 在重建特征上的表現(xiàn)明顯優(yōu)于簡(jiǎn)單的基線以及最新的最先進(jìn)的方法 [2-3]。

FP 在特征缺失率高 (>90%) 的情況下尤為突出，而所有其他方法往往會(huì)受到影響。 例如，即使丟失了 99% 的特征，與所有特征都存在的相同模型相比，F(xiàn)P 平均僅損失約 4% 的相對(duì)準(zhǔn)確度。

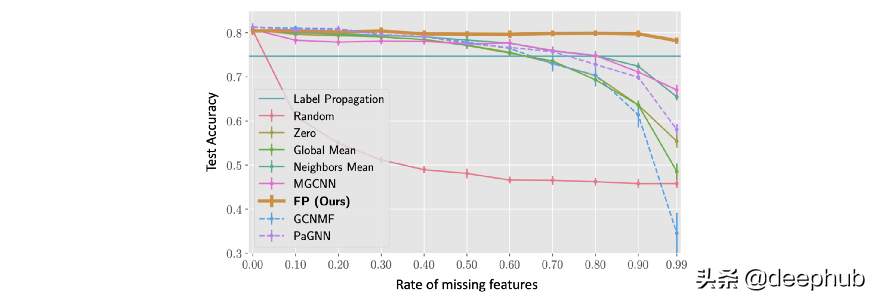
Cora 數(shù)據(jù)集上不同特征缺失率的節(jié)點(diǎn)分類準(zhǔn)確度(從 0% 是大多數(shù) GNN 的標(biāo)準(zhǔn)狀態(tài)到 99% 的極端情況)。

FP 的另一個(gè)關(guān)鍵特點(diǎn)是它的可擴(kuò)展性： 其他方法無法擴(kuò)展到具有幾百萬條邊的圖之外，但 FP 可以擴(kuò)展到十億條邊的圖。 作者用了不到一小時(shí)的時(shí)間在內(nèi)部 Twitter 圖表上運(yùn)行它，使用單臺(tái)機(jī)器大約有 10 億個(gè)節(jié)點(diǎn)和 100 億條邊。

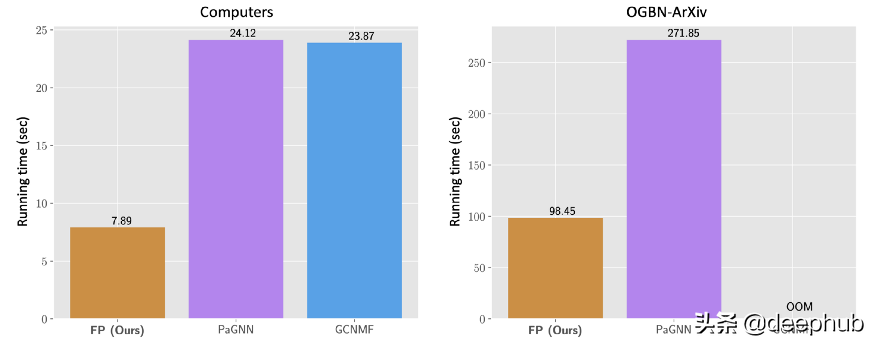
FP+GCN 和最新最先進(jìn)的方法 GCNMF 和 PaGNN [2-3] 的運(yùn)行時(shí)間(以秒為單位)。 FP+GCN 比其他兩種方法快 3 倍。 GCNMF 在 OGBN-Arxiv 上出現(xiàn)內(nèi)存不足 (OOM)，而 GCNMF 和 PaGNN 在 OGBN-Products(約 123M 邊)上出現(xiàn) OOM，其中 FP 的重建部分(無需訓(xùn)練下游模型)僅需約 10 秒。

FP 的當(dāng)前限制之一是它在heterophilic graphs上效果不佳，即鄰居具有不同特征的圖。 這并不奇怪，因?yàn)?FP 源自同質(zhì)假設(shè)(通過擴(kuò)散方程最小化 Dirichlet energy)。 FP 假設(shè)不同的特征通道是不相關(guān)的，這在現(xiàn)實(shí)生活中很少見。 但是可以通過替代更復(fù)雜的擴(kuò)散機(jī)制，同時(shí)滿足這兩個(gè)限制。

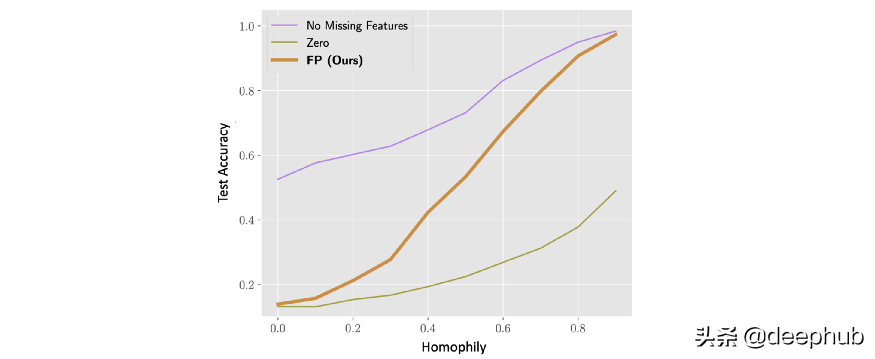
當(dāng) 99% 的特征缺失時(shí)，具有各種同質(zhì)性水平的合成圖上的節(jié)點(diǎn)分類準(zhǔn)確度(0 是極度異質(zhì)性，1 是極度同質(zhì)性)。 雖然在高度同質(zhì)性設(shè)置中 FP 的表現(xiàn)幾乎與具有完整特征的情況一樣好，但在低同質(zhì)性設(shè)置中，兩者之間的差距很大，并且 FP 的性能惡化到一個(gè)簡(jiǎn)單的基線，其中缺失的特征被替換為 零。

盡管在實(shí)際應(yīng)用中無處不在，但在缺少節(jié)點(diǎn)特征的圖上學(xué)習(xí)是一個(gè)幾乎未被探索的研究領(lǐng)域。 特征傳播模型是提高在缺少節(jié)點(diǎn)特征的圖上學(xué)習(xí)能力的重要一步，它還提出了關(guān)于在這種情況下學(xué)習(xí)的理論能力的深刻問題。 FP 的簡(jiǎn)單性和可擴(kuò)展性，以及與更復(fù)雜的方法相比的驚人的好結(jié)果，即使在極端缺失的特征狀態(tài)下，也使其成為大規(guī)模工業(yè)應(yīng)用的良好候選者。