一文解讀貝塞爾修正:樣本方差為何用 n?1而非n?
前幾天使用duckdb進行數據分析過程中,發現結果不一致,仔細翻閱Duckdb文檔中stddev_pop和stddev_samp、var_pop和var_samp 的描述和公式差異:
- stddev_pop(x):總體標準差

- stddev_samp(x):樣本標準差

- var_pop(x):總體方差(無貝塞爾修正)

- var_samp(x):樣本方差(包含貝塞爾修正)

為什么會有兩個標準差、兩個方差的定義,為啥一個除以n而另一個除以n-1;為何要貝塞爾修正(Bessel’s Correction)?
總體方差和樣本方差
在統計分析中,總體方差和樣本方差是衡量數據分散程度的重要指標。總體方差(The population variance)是描述整個數據集的離散程度,也就是說我們手上的數據集是整個數據集,它計算的是數據點與總體均值的差異程度。總體方差的公式如下:

其中 n 是數據集的數據點數量。在計算總體方差時,我們可以直接使用 n 作為除數,因為我們已經有了整個數據集的所有信息。
與此相對,樣本方差(The sample variance)是從總體中抽取的樣本數據的離散程度,也就是我們計算的數據集只是整體的一部分,通過手上的數據集來估計總體的方差,例如在產品質量分析過程,我們檢驗的產品可能只是所有產品的抽樣部分檢測。由于樣本數據僅是總體的一個子集,它不包含所有的信息,因此樣本方差往往會低估總體方差。為了彌補這一點,我們需要進行貝塞爾修正,將除數從 n 調整為 n?1,這樣可以更準確地估計總體方差。樣本方差的公式如下:

對于標準差,總體標準差(The population standard deviation)是總體方差的平方根,而樣本標準差(he sample standard deviation)則是樣本方差的平方根。標準差與方差的區別在于,標準差與原始數據的單位相同,更便于解釋。
貝塞爾修正
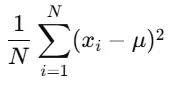
為什么在(貝塞爾修正)計算樣本方差時除以 n?1,我們需要分析使用樣本均值代替總體均值時會發生什么。在實際應用中,我們通常只能依賴樣本數據。其原理如下:
計算樣本方差時,我們會找到每個數據點與樣本均值的偏差,平方這些偏差,并計算它們的平均值。然而,樣本均值通常不等于總體均值,這導致使用樣本均值會低估總體的方差或分布。
以下是幾種可能的情況:
1. 樣本均值小于總體均值(xˉ<μ)時的情況
當樣本均值(xˉ)小于總體均值(μ)時,樣本中的大部分數據點離樣本均值更近,而不是離總體均值更近。結果是,數據點與均值之間的距離(偏差)變小,導致方差的計算偏小,即低估了實際的方差。因為我們只能從樣本中獲取數據,無法收集所有總體數據。在樣本數據中,接近總體均值的一部分數據的偏差(絕對值或平方差)會大于樣本均值的偏差,而接近樣本均值的部分數據偏差則更小。由于正態分布的對稱性,低估的區域大于高估的區域,因此方差會被低估。
為了補償方差的低估,使用 n?1代替 n 來計算方差,這就是貝塞爾修正(Bessel’s Correction)。
2. 樣本均值大于總體均值(xˉ>μ)時的情況
當樣本均值大于總體均值時,低值部分的數據點會比總體均值更接近樣本均值,依然導致方差的低估。同樣地,由于正態分布的對稱性,低估的區域依然大于高估的區域,因此我們通過將偏差除以 n?1 來修正這種低估,確保樣本方差是總體方差的無偏估計。
無論是樣本均值小于總體均值還是大于總體均值,都會導致方差的低估。通過貝塞爾修正(使用 n?1而非 n)可以補償這種低估,使得樣本方差更加接近總體方差,從而得到無偏的估計。
貝塞爾修正(Bessel’s Correction)的核心在于將樣本數據的方差除以 n?1,而不是 n,這種修正確保了我們在使用樣本數據來估算總體方差時,得到的是一個無偏估計。無偏估計的意思是,隨著樣本數量的增加,估算的樣本方差會逐漸趨近于總體方差。
貝塞爾修正(Bessel’s Correction)的好處在于,它修正了由于樣本均值比總體均值更接近樣本數據的現象,避免了方差估計的系統性偏差。舉個例子,如果我們直接使用樣本均值來計算樣本方差(除以 n),可能會低估樣本數據的離散程度,從而導致我們對總體方差的估計值偏小。通過貝塞爾修正,我們的樣本方差可以更好地反映總體方差的真實情況。
在計算樣本方差或標準差時,除以 n?1看似一個微小的變化,但它對于獲得總體方差的無偏估計至關重要。這個調整稱為貝塞爾修正,它補償了由于依賴樣本均值而非真實總體均值所導致的低估問題。