基于PyTorch從零實現視覺轉換器(ViT)? 原創
譯者 | 朱先忠
審校 | 重樓
簡介
視覺轉換器(Vision Transformer,通常縮寫為“ViT”)可以被視為計算機視覺領域的重大突破技術。當涉及到與視覺相關的任務時,人們通常使用基于CNN(卷積神經網絡)的模型來解決。到目前為止,這些模型的性能總是優于任何其他類型的神經網絡。直到2020年,Dosovitskiy等人發表了一篇題為《一張圖頂16×16個單詞:大規模圖像識別的轉換器》的論文(參考文獻1),論文中強調這種轉換器能夠提供比傳統卷積神經網絡更好的能力。
傳統卷積神經網絡中的單個卷積層通過使用核提取特征來工作。由于內核的大小與輸入圖像相比相對較小,因此它只能捕獲該小區域內包含的信息。換句話說,它側重于提取局部特征。為了理解圖像的全局上下文,需要使用由多個卷積層組成的一個棧結構。ViT解決了這個問題,因為它實現了直接從初始層捕獲全局信息。因此,在ViT中堆疊多個卷積層可以實現更全面的信息提取。

圖1:通過堆疊多個卷積層,CNN可以實現更大的感受野,這對于捕捉圖像的全局上下文至關重要(參考文獻2)
視覺轉換器架構
如果你曾經學習過轉換器,你應該熟悉編碼器和解碼器這兩個術語。在NLP(自然語言處理)領域,特別是對于機器翻譯等任務,編碼器負責捕獲輸入序列中標記(即單詞)之間的關系,而解碼器負責生成輸出序列。在ViT的情況下,我們只需要編碼器部分,它將圖像的每個圖塊視為一個標記。基于同樣的想法,編碼器能夠找到圖塊之間的關系。
整個視覺轉換器架構如圖2所示。在我們詳細討論有關代碼之前,我將先使用以下幾小節來解釋此架構的每個組件。
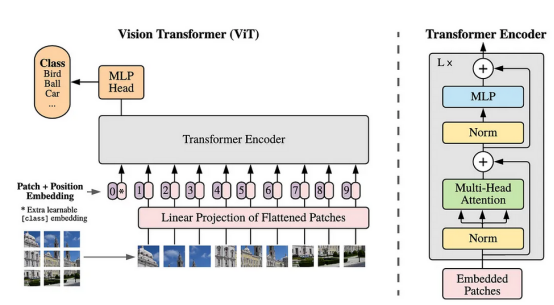
圖2:視覺轉換器架構(參考文獻1)
圖塊扁平化和線性投影
根據上圖,我們可以看到,要做的第一步是將圖像劃分為圖塊。所有這些圖塊排列成一個序列。然后,這些圖塊中的每一個都被扁平化,每個圖塊都形成一個一維陣列。然后,通過線性投影將這些標記的序列投影到更高維的空間中。此時,我們可以將投影結果視為NLP中的單詞嵌入,即表示單個單詞的向量。從技術上講,線性投影過程可以用簡單的MLP(多層感知機)或卷積層來完成。稍后,我將在具體的實施過程中對此進行更多的解釋。
類標記和位置嵌入
由于我們正在處理分類任務,我們需要在投影的圖塊序列前添加一個新的標記。這個標記稱為類標記,它將通過為每個圖塊分配重要性權重來聚合其他圖塊的信息。值得注意的是,圖塊扁平化和線性投影會導致模型丟失空間信息。因此,為了解決這個問題,所有標記(包括類標記)都添加了位置嵌入,以便重新引入空間信息。
轉換器編碼器和MLP頭
在這個階段,張量已經準備好,將被饋送到轉換器編碼器塊中,其詳細結構可以在圖2的右側看到。該塊由四個部分組成:層規一化、多頭注意力、另一層規一化和MLP層。值得注意的是,這里實現了兩個殘差連接。轉換器編碼器塊左上角的L×表示將根據要構建的模型大小重復L次。
最后,我們將把編碼器塊連接到MLP頭。請記住,要轉發的張量只是從類標記部分出來的張量。MLP頭部本身由一個完全連接的層和一個輸出層組成,其中輸出層中的每個神經元代表數據集中一個可用的類。
視覺轉換器變體
在原始論文中提出了三種ViT變體,即ViT-B、ViT-L和ViT-H,如圖3所示,其中:
- Layers(L):轉換器編碼器的數量。
- Hidden size(D):嵌入維度以表示單個圖塊。
- MLP size:MLP隱藏層中的神經元數量。
- Heads:多頭注意力層中的注意力頭數。
- Params:模型的參數數量。
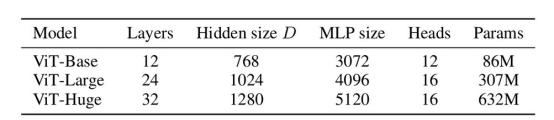
圖3:三種視覺轉換器變體的詳細信息(參考文獻1)
在本文中,我想使用PyTorch框架從頭開始實現一個ViT-Base架構。順便說一句,該模塊本身實際上還提供了幾個預訓練的ViT模型(參考文獻3),即ViT_b_16、ViT_b_32、ViT_l_16、ViT_l_32和ViT_h_14,其中作為這些模型后綴的數字是指使用的圖塊大小。
從頭開始實現一個ViT
現在,讓我們開始真正有趣的部分。實現一個ViT編程首先要做的是導入模塊。在這種情況下,我們將只依賴PyTorch框架的功能來構建ViT架構。從torchinfo加載的summary()函數將幫助我們顯示模型的詳細信息。
# 代碼塊1
import torch
import torch.nn as nn
from torchinfo import summary參數配置
在代碼塊2中,我們將初始化幾個變量來配置模型。在這里,我們假設單個批次中要處理的圖像數量僅為1,其維度為3×224×224(標記為#(1))。我們在這里要使用的變體是ViT-Base,這意味著我們需要將圖塊大小設置為16,注意頭數量設置為12,編碼器數量設置為12,嵌入維度設置為768(#(2))。通過使用此配置,圖塊數量將為196(#(3))。這個數字是通過將大小為224×224的圖像劃分為16×16個圖塊而獲得的,其中它產生了14×14的網格。因此,一張圖像將有196個圖塊。
我們還將對dropout層使用0.1的速率(#(4))。值得注意的是,論文中沒有明確提及dropout層的使用。由于在構建深度學習模型時,使用這些層可以被視為一種標準做法,因此我無論如何都會實現它。我們假設數據集中有10個類,相應地設置了NUM_classes變量。
# 代碼塊2
#(1)
BATCH_SIZE = 1
IMAGE_SIZE = 224
IN_CHANNELS = 3
#(2)
PATCH_SIZE = 16
NUM_HEADS = 12
NUM_ENCODERS = 12
EMBED_DIM = 768
MLP_SIZE = EMBED_DIM * 4 # 768*4 = 3072
#(3)
NUM_PATCHES = (IMAGE_SIZE//PATCH_SIZE) ** 2 # (224//16)**2 = 196
#(4)
DROPOUT_RATE = 0.1
NUM_CLASSES = 10由于本文的重點是實現模型,因此我不會談論如何訓練它。但是,如果你想這樣做,你需要確保你的機器上安裝了GPU,因為它可以使訓練更快。下面的代碼塊3用于檢查PyTorch是否成功檢測到你的Nvidia GPU。
# 代碼塊3
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
# 代碼塊3 output
cuda圖塊扁平化和線性投影實現
我之前提到過,圖塊扁平化和線性投影操作可以通過使用簡單的MLP或卷積層來完成。在這里,我將在PatcherUnfold()和PatcherConv()類中實現它們。稍后,你可以選擇在主ViT類中實現這兩個類中的任何一個。
讓我們先從PatcherUnfold()開始,詳細信息可以在代碼塊4中看到。在這里,我使用了一個nn.Unfold()層。在標注有#(1)的行處可以看到,其kernel_size和步幅均為PATCH_SIZE(16)。通過這種配置,該層將對輸入圖像應用一個不重疊的滑動窗口。在每一步中,內部的圖塊都會被壓平。請看下面的圖4,以查看此操作的圖形化展示。在該圖中,我們使用大小為2的核和步幅對大小為4×4的圖像應用展開操作。
# 代碼塊4
class PatcherUnfold(nn.Module):
def __init__(self):
super().__init__()
self.unfold = nn.Unfold(kernel_size=PATCH_SIZE, stride=PATCH_SIZE) #(1)
self.linear_projection = nn.Linear(in_features=IN_CHANNELS*PATCH_SIZE*PATCH_SIZE,
out_features=EMBED_DIM) #(2)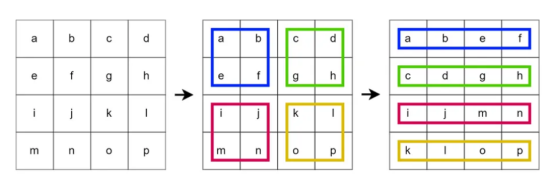
圖4:在4×4圖像上應用具有核大小和步幅2的展開操作
接下來,使用一個標準的nn.Linear()層(#(2))進行線性投影操作。為了使輸入與扁平化的圖塊匹配,我們需要使用In_CHANNELS*patch_SIZE*patch_SIZE作為In_features參數,即16×16×3=768。然后,我使用設置大小為EMBED_DIM的out_features參數來確定投影結果維度(768)。值得注意的是,投影結果和扁平化的圖塊具有完全相同的尺寸,如ViT-B架構所規定的。如果要實現ViT-L或ViT-H,則應將投影結果維度分別更改為1024或1280,其大小可能不再與扁平化的圖塊相同。
因為nn.Unfold()和nn.Linear()層已經初始化,所以現在我們必須使用下面的forward()函數連接這些層。我們需要注意的一件事是,展開張量的第一和第二軸需要使用permute() 方法進行交換(#(1))。這是因為我們想將扁平的圖塊視為一系列標記,類似于NLP模型中處理標記的方式。我還打印出代碼塊中每個進程的形狀,以幫助你跟蹤分析數組的維度。
# 代碼塊5
def forward(self, x):
print(f'original\t: {x.size()}')
x = self.unfold(x)
print(f'after unfold\t: {x.size()}')
x = x.permute(0, 2, 1) #(1)
print(f'after permute\t: {x.size()}')
x = self.linear_projection(x)
print(f'after lin proj\t: {x.size()}')
return x此時,PatcherUnfold()類已經完成。為了檢查它是否正常工作,我們可以嘗試向它提供一個隨機值的張量,該張量模擬大小為224×224的單個RGB圖像。
# 代碼塊6
patcher_unfold = PatcherUnfold()
x = torch.randn(1, 3, 224, 224)
x = patcher_unfold(x)你可以看到下面的輸出,我們的原始圖像已成功轉換為形狀1×196×768,其中1表示單批中的圖像數量,196表示序列長度(圖塊數量),768是嵌入維度。
# 代碼塊6 輸出
original : torch.Size([1, 3, 224, 224])
after unfold : torch.Size([1, 768, 196])
after permute : torch.Size([1, 196, 768])
after lin proj : torch.Size([1, 196, 768])這就是使用PatcherUnfold()類實現圖塊扁平化展開和線性投影的過程。我們實際上也可以使用PatcherConv()實現同樣的事情,代碼如下所示:
# 代碼塊7
class PatcherConv(nn.Module):
def __init__(self):
super().__init__()
self.conv = nn.Conv2d(in_channels=IN_CHANNELS,
out_channels=EMBED_DIM,
kernel_size=PATCH_SIZE,
stride=PATCH_SIZE)
self.flatten = nn.Flatten(start_dim=2)
def forward(self, x):
print(f'original\t\t: {x.size()}')
x = self.conv(x) #(1)
print(f'after conv\t\t: {x.size()}')
x = self.flatten(x) #(2)
print(f'after flatten\t\t: {x.size()}')
x = x.permute(0, 2, 1) #(3)
print(f'after permute\t\t: {x.size()}')
return x這種方法可能看起來不像前一種方法那么簡單,因為它實際上并沒有使圖塊變扁平。相反,它使用具有EMBED_DIM(768)個內核的卷積層,從而產生具有768個通道的14×14圖像(#(1))。為了獲得與PatcherUnfold()相同的輸出維度,我們將空間維度展平(#(2)),并交換得到張量的第一和第二軸(#(3))。為此,你可以分析下面代碼塊8的輸出,并查看每一步后的詳細的張量形狀。
# 代碼塊8
patcher_conv = PatcherConv()
x = torch.randn(1, 3, 224, 224)
x = patcher_conv(x)
# 代碼塊8 output
original : torch.Size([1, 3, 224, 224])
after conv : torch.Size([1, 768, 14, 14])
after flatten : torch.Size([1, 768, 196])
after permute : torch.Size([1, 196, 768])值得注意的是,在PatcherUnfold()中使用nn.Conv2d()實現單獨展開和線性投影,相比于PatcherConv()更有效,因為它將兩個步驟組合成一個操作。
類標記和位置嵌入實現
在將所有圖塊投影到嵌入維度并排列成序列后,下一步是將類標記放在序列中的第一個圖塊標記之前。此過程與PosEmbedding()類中的位置嵌入實現打包在一起,如代碼塊9所示:
# 代碼塊9
class PosEmbedding(nn.Module):
def __init__(self):
super().__init__()
self.class_token = nn.Parameter(torch.randn(size=(BATCH_SIZE, 1, EMBED_DIM)),
requires_grad=True) #(1)
self.pos_embedding = nn.Parameter(torch.randn(size=(BATCH_SIZE, NUM_PATCHES+1, EMBED_DIM)),
requires_grad=True) #(2)
self.dropout = nn.Dropout(p=DROPOUT_RATE) #(3)類標記本身使用nn.Parameter()初始化。本質上,nn.Parameter()是一個權重張量(#(1))。此張量的大小需要與嵌入維度和批大小相匹配,以便它可以與現有的標記序列連接。這個張量最初包含隨機值,這些值將在訓練過程中更新。為了允許更新它,我們需要將requires_grad參數設置為True。同樣,我們也需要使用nn.Parameter()來創建位置嵌入(#(2)),但形狀不同。在這種情況下,我們將序列維度設置為比原始序列長一個標記,以容納我們剛剛創建的類標記。不僅如此,在這里,我還使用我們之前指定的速率(#(3))初始化了一個dropout層。
之后,我將用下面代碼塊10中的forward()函數連接這些層。此函數接受的張量將使用torch.cat()與class_token連接,如#(1)標記的行所示。接下來,我們將在結果輸出和位置嵌入張量(#(2))之間執行元素相加,然后再將其傳遞到dropout層(#(3))。
# 代碼塊10
def forward(self, x):
class_token = self.class_token
print(f'class_token dim\t\t: {class_token.size()}')
print(f'before concat\t\t: {x.size()}')
x = torch.cat([class_token, x], dim=1) #(1)
print(f'after concat\t\t: {x.size()}')
x = self.pos_embedding + x #(2)
print(f'after pos_embedding\t: {x.size()}')
x = self.dropout(x) #(3)
print(f'after dropout\t\t: {x.size()}')
return x像往常一樣,讓我們嘗試通過這個網絡向前傳播一個張量,看看它是否按預期工作。請記住,pos_embedding模型的輸入本質上是PatcherUnfold()或PatcherConv()產生的張量。
# 代碼塊11
pos_embedding = PosEmbedding()
x = pos_embedding(x)如果我們仔細看看每一步的張量維數,我們可以觀察到張量x的大小最初是1×196×768。在類標記之前添加后,維度變為1×197×768。
# 代碼塊11輸出
class_token dim : torch.Size([1, 1, 768])
before concat : torch.Size([1, 196, 768])
after concat : torch.Size([1, 197, 768])
after pos_embedding : torch.Size([1, 197, 768])
after dropout : torch.Size([1, 197, 768])轉換器編碼器實現
如果我們回顧一下圖2,可以看到轉換器編碼器塊由四個組件組成。我們將在下面顯示的TransformerEncoder()類中定義所有這些組件。
# 代碼塊12
class TransformerEncoder(nn.Module):
def __init__(self):
super().__init__()
self.norm_0 = nn.LayerNorm(EMBED_DIM) #(1)
self.multihead_attention = nn.MultiheadAttention(EMBED_DIM, #(2)
num_heads=NUM_HEADS,
batch_first=True,
dropout=DROPOUT_RATE)
self.norm_1 = nn.LayerNorm(EMBED_DIM) #(3)
self.mlp = nn.Sequential( #(4)
nn.Linear(in_features=EMBED_DIM, out_features=MLP_SIZE), #(5)
nn.GELU(),
nn.Dropout(p=DROPOUT_RATE),
nn.Linear(in_features=MLP_SIZE, out_features=EMBED_DIM), #(6)
nn.Dropout(p=DROPOUT_RATE)
)標記為#(1)和#(3)的行處的兩個歸一化步驟是使用nn.LayerNorm()實現的。請記住,我們在這里使用的層規一化不同于我們在CNN中常見的批規一化。批歸一化是通過對批中所有樣本中單個特征內的值進行歸一化來實現的。同時,在層歸一化中,單個樣本中的所有特征都將被歸一化。請看下圖5,以更好地說明這一概念。在這個例子中,我們假設每一行代表一個樣本,而每一列都是一個特征。相同顏色的單元格表示它們的值一起歸一化。
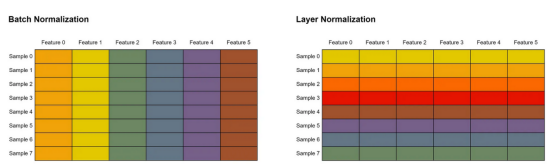
圖5:批次歸一化和層歸一化之間差異展示(批規一化在批維度上進行規一化,而層規一化在特征維度上進行標準化)
隨后,我們初始化一個nn.Multihead Attention()層,在代碼塊12中標記為#(2)的行處輸入大小為EMBED_DIM(768)。batch_first參數設置為True,表示批處理維度位于輸入張量的第0軸。一般來說,多頭注意力本身允許模型同時捕捉圖像塊之間的各種關系。多頭注意力中的每一個頭都集中在這些關系的不同方面。稍后,該層接受三個輸入:查詢、鍵和值,這些都是計算所謂的注意力權重所必需的。通過這樣做,這一層可以了解每個圖塊應該在多大程度上關注其他圖塊。換句話說,這種機制允許該層捕獲兩個或多個圖塊之間的關系。ViT中采用的注意力機制可以被視為整個模型的核心,因為這個組件本質上是允許ViT在圖像識別任務中超越CNN性能的組件。
轉換器編碼器內的MLP組件是使用nn.Sequential()構造的(#(4))。在這里,我們實現了兩個連續的線性層,每個層后面都有一個dropout層。我們還需要將GELU激活函數放在第一個線性層之后。第二個線性層不使用激活函數,因為它的目的只是將張量投影回原始嵌入維度。
現在,是時候使用下面的代碼塊連接我們剛剛初始化的所有層了。
# 代碼塊13
def forward(self, x):
residual = x #(1)
print(f'residual dim\t\t: {residual.size()}')
x = self.norm_0(x) #(2)
print(f'after norm\t\t: {x.size()}')
x = self.multihead_attention(x, x, x)[0] #(3)
print(f'after attention\t\t: {x.size()}')
x = x + residual #(4)
print(f'after addition\t\t: {x.size()}')
residual = x #(5)
print(f'residual dim\t\t: {residual.size()}')
x = self.norm_1(x) #(6)
print(f'after norm\t\t: {x.size()}')
x = self.mlp(x) #(7)
print(f'after mlp\t\t: {x.size()}')
x = x + residual #(8)
print(f'after addition\t\t: {x.size()}')
return x在上述forward()函數中,我們首先將輸入張量x存儲到殘差變量(#(1))中,在該變量中,它用于創建殘差連接。接下來,我們在將輸入張量(#(2))輸入到多頭注意力層(#(3))之前對其進行歸一化。正如我之前提到的,這一層將查詢、鍵和值作為輸入。在這種情況下,張量x將被用作三個參數的參數。請注意,我在代碼的同一行也寫了[0]。這主要是因為一個nn.MultiheadAttention()對象返回兩個值:注意力輸出和注意力權重;在這種情況下,我們只需要前者。接下來,在標記為#(4)的行處,我們在多頭注意力層的輸出和原始輸入張量之間執行元素相加。然后,在執行第一次殘差運算后,我們直接用當前張量x(#(5))更新殘差變量。在將張量饋送到MLP塊(#(7))并執行另一個元素相加操作(#(8))之前,在第#(6)行完成第二次歸一化操作。
我們可以使用下面的代碼塊14檢查我們的轉換器編碼器塊實現是否正確。請記住,transformer_encoder模型的輸入必須是PosEmbedding()產生的輸出。
# 代碼塊14
transformer_encoder = TransformerEncoder()
x = transformer_encoder(x)
# 代碼塊14 output
residual dim : torch.Size([1, 197, 768])
after norm : torch.Size([1, 197, 768])
after attention : torch.Size([1, 197, 768])
after addition : torch.Size([1, 197, 768])
residual dim : torch.Size([1, 197, 768])
after norm : torch.Size([1, 197, 768])
after mlp : torch.Size([1, 197, 768])
after addition : torch.Size([1, 197, 768])從上面的輸出中可以看出,每一步之后張量維度都沒有變化。但是,如果你仔細看看MLP塊是如何在代碼塊12中構造的,你會發現它的隱藏層在#(5)標記的行處擴展為MLP_SIZE(3072)。然后,我們直接將其投影回其原始尺寸,即第6行的EMBED_DIM(768)。
實現MLP頭編程
我們要實現的最后一個類是MLPHead()。就像轉換器編碼器塊內的MLP層一樣,MLPHead()也包括一些全連接層、GELU激活函數和層規一化。這個類的完整的實現代碼如下所示:
# 代碼塊15
class MLPHead(nn.Module):
def __init__(self):
super().__init__()
self.norm = nn.LayerNorm(EMBED_DIM)
self.linear_0 = nn.Linear(in_features=EMBED_DIM,
out_features=EMBED_DIM)
self.gelu = nn.GELU()
self.linear_1 = nn.Linear(in_features=EMBED_DIM,
out_features=NUM_CLASSES) #(1)
def forward(self, x):
print(f'original\t\t: {x.size()}')
x = self.norm(x)
print(f'after norm\t\t: {x.size()}')
x = self.linear_0(x)
print(f'after layer_0 mlp\t: {x.size()}')
x = self.gelu(x)
print(f'after gelu\t\t: {x.size()}')
x = self.linear_1(x)
print(f'after layer_1 mlp\t: {x.size()}')
return x在上面實現代碼中,需要注意的一點是,第二個全連接層基本上是整個ViT架構的輸出(#(1))。因此,我們需要確保神經元的數量與我們要訓練模型的數據集中可用的種類的數量相匹配。在這種情況下,我假設我們有EMBED_DIM(10)個類。此外,值得注意的是,我最后沒有使用softmax層,因為它已經在nn網絡中實現了。如果你想真正訓練這個模型,可以使用一下CrossEntropyLoss()。
為了測試MLPHead()模型,我們首先需要對轉換器編碼器塊產生的張量進行切片,如代碼塊16中的第#(1)行所示。這是因為我們想獲取符號序列中的第0個元素,它對應于我們之前在圖塊符號序列前面添加的類標記。
# 代碼塊16
x = x[:, 0] #(1)
mlp_head = MLPHead()
x = mlp_head(x)
# 代碼塊16 output
original : torch.Size([1, 768])
after norm : torch.Size([1, 768])
after layer_0 mlp : torch.Size([1, 768])
after gelu : torch.Size([1, 768])
after layer_1 mlp : torch.Size([1, 10])當運行上述測試代碼時,我們可以看到最終的張量形狀是1×10,這正是我們所期望的。
整個ViT架構
此時,所有ViT組件都已成功創建。因此,我們現在可以使用它們來構建整個視覺轉換器架構了。請分析一下下面的代碼塊,看看我是怎么做到的。
# 代碼塊17
class ViT(nn.Module):
def __init__(self):
super().__init__()
#self.patcher = PatcherUnfold()
self.patcher = PatcherConv() #(1)
self.pos_embedding = PosEmbedding()
self.transformer_encoders = nn.Sequential(
*[TransformerEncoder() for _ in range(NUM_ENCODERS)] #(2)
)
self.mlp_head = MLPHead()
def forward(self, x):
x = self.patcher(x)
x = self.pos_embedding(x)
x = self.transformer_encoders(x)
x = x[:, 0] #(3)
x = self.mlp_head(x)
return x關于上述代碼,我想強調幾點。首先,在第1行,我們可以使用PatcherUnfold()或PatcherConv(),因為它們都有相同的作用,即執行圖塊展平和線性投影步驟。在這種情況下,我選用了后者。其次,轉換器編碼器塊將重復NUM_Encoder(12)次(#(2)),因為我們將實現如圖3所示的ViT-Base。最后,不要忘記對轉換器編碼器輸出的張量進行切片,因為我們的MLP頭只會處理輸出的類標記部分(#(3))。
我們可以使用以下代碼測試ViT模型是否正常工作。
# 代碼塊18
vit = ViT().to(device)
x = torch.randn(1, 3, 224, 224).to(device)
print(vit(x).size())你可以在這里看到,維度為1×3×224×224的輸入已轉換為1×10,這表明我們的模型按預期工作。
注意:你需要注釋掉所有打印內容,使輸出結果看起來更簡潔一些。
# 代碼塊18 輸出
torch.Size([1, 10])此外,我們還可以使用我們在代碼開頭導入的summary()函數查看網絡的詳細結構。你可以觀察到,參數的總數約為8600萬,與圖3中所示的數字相匹配。
# 代碼塊19
summary(vit, input_size=(1,3,224,224))
# 代碼塊19 輸出
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
ViT [1, 10] --
├─PatcherConv: 1-1 [1, 196, 768] --
│ └─Conv2d: 2-1 [1, 768, 14, 14] 590,592
│ └─Flatten: 2-2 [1, 768, 196] --
├─PosEmbedding: 1-2 [1, 197, 768] 152,064
│ └─Dropout: 2-3 [1, 197, 768] --
├─Sequential: 1-3 [1, 197, 768] --
│ └─TransformerEncoder: 2-4 [1, 197, 768] --
│ │ └─LayerNorm: 3-1 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-2 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-3 [1, 197, 768] 1,536
│ │ └─Sequential: 3-4 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-5 [1, 197, 768] --
│ │ └─LayerNorm: 3-5 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-6 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-7 [1, 197, 768] 1,536
│ │ └─Sequential: 3-8 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-6 [1, 197, 768] --
│ │ └─LayerNorm: 3-9 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-10 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-11 [1, 197, 768] 1,536
│ │ └─Sequential: 3-12 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-7 [1, 197, 768] --
│ │ └─LayerNorm: 3-13 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-14 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-15 [1, 197, 768] 1,536
│ │ └─Sequential: 3-16 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-8 [1, 197, 768] --
│ │ └─LayerNorm: 3-17 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-18 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-19 [1, 197, 768] 1,536
│ │ └─Sequential: 3-20 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-9 [1, 197, 768] --
│ │ └─LayerNorm: 3-21 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-22 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-23 [1, 197, 768] 1,536
│ │ └─Sequential: 3-24 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-10 [1, 197, 768] --
│ │ └─LayerNorm: 3-25 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-26 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-27 [1, 197, 768] 1,536
│ │ └─Sequential: 3-28 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-11 [1, 197, 768] --
│ │ └─LayerNorm: 3-29 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-30 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-31 [1, 197, 768] 1,536
│ │ └─Sequential: 3-32 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-12 [1, 197, 768] --
│ │ └─LayerNorm: 3-33 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-34 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-35 [1, 197, 768] 1,536
│ │ └─Sequential: 3-36 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-13 [1, 197, 768] --
│ │ └─LayerNorm: 3-37 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-38 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-39 [1, 197, 768] 1,536
│ │ └─Sequential: 3-40 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-14 [1, 197, 768] --
│ │ └─LayerNorm: 3-41 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-42 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-43 [1, 197, 768] 1,536
│ │ └─Sequential: 3-44 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-15 [1, 197, 768] --
│ │ └─LayerNorm: 3-45 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-46 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-47 [1, 197, 768] 1,536
│ │ └─Sequential: 3-48 [1, 197, 768] 4,722,432
├─MLPHead: 1-4 [1, 10] --
│ └─LayerNorm: 2-16 [1, 768] 1,536
│ └─Linear: 2-17 [1, 768] 590,592
│ └─GELU: 2-18 [1, 768] --
│ └─Linear: 2-19 [1, 10] 7,690
==========================================================================================
Total params: 86,396,938
Trainable params: 86,396,938
Non-trainable params: 0
Total mult-adds (Units.MEGABYTES): 173.06
==========================================================================================
Input size (MB): 0.60
Forward/backward pass size (MB): 102.89
Params size (MB): 231.59
Estimated Total Size (MB): 335.08
==========================================================================================總結
上面所有這些內容幾乎都與視覺轉換器架構有關。如果你發現代碼中存在任何錯誤,歡迎隨時發表評論。
本文中使用的所有代碼也可以在我的GitHub存儲庫中找到。此代碼的鏈接地址是https://github.com/MuhammadArdiPutra/medium_articles/blob/main/Paper%20Walkthrough%20-%20Vision%20Transformer%20(ViT).ipynb。
參考資料
【1】Alexey Dosovitskiy等人。《An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale》(一張圖頂16×16個單詞:用于大規模圖像識別的轉換器)。Arxiv,https://arxiv.org/pdf/2010.11929。
【2】林浩寧等。《Maritime Semantic Labeling of Optical Remote Sensing Images with Multi-Scale Fully Convolutional Network》(基于多尺度全卷積網絡的光學遙感圖像海洋語義標注)。Research Gate,https://www.researchgate.net/publication/316950618_Maritime_Semantic_Labeling_of_Optical_Remote_Sensing_Images_with_Multi-Scale_Fully_Convolutional_Network。
【3】《Vision Transformer. PyTorch》(基于PyTorch框架的視覺轉換器實現)。
???Https://pytorch.org/vision/main/models/vision_transformer.html。??
譯者介紹
朱先忠,51CTO社區編輯,51CTO專家博客、講師,濰坊一所高校計算機教師,自由編程界老兵一枚。
原文標題:??Paper Walkthrough: Vision Transformer (ViT)??,作者:Muhammad Ardi

















