考慮下面這個連續概率分布的概率密度函數，它表示的是從A點到B點可能花費的時間。

這是一個連續隨機變量t取值區間為[1,5]的均勻分布，其概率密度函數可以表示成下面形式。

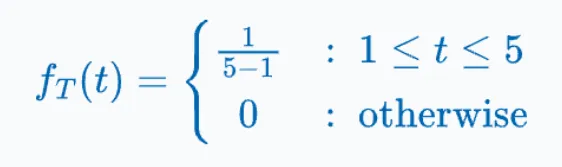
那么，問題來了！

Q）他從A點到達B點花費3分鐘的概率P(T=3)是多少？

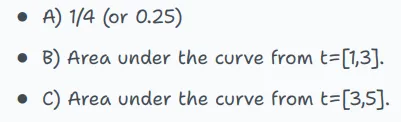
哇哦！上述答案都是錯的，正確答案是：0。

有的人可能會立馬抗議，并表示為什么在擲色子中每個點的概率就是1/6呢？

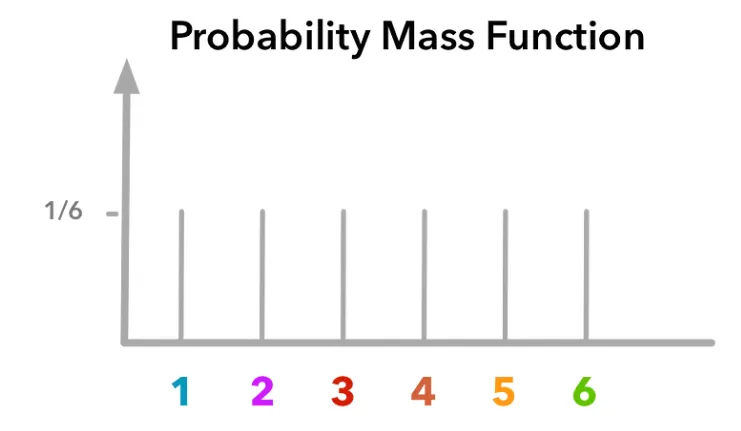
因為擲色子實驗結果是離散的，離散隨機變量的概率分布稱為概率質量函數（PMF），PMF中的每個值代表的就是概率。

而連續隨機變量的概率分布稱為概率密度函數（PDF），PDF中每個點對應的值不是概率，而是概率密度，也就是在該點附近取值的相對可能性。

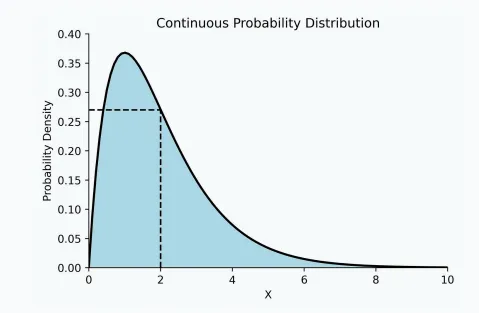
是不是有點繞？不過沒關系，只要知道它不是概率就行了，后面我們講似然的時候還會提到。

對于概率密度函數，我們只能通過積分來計算某個區間的概率。

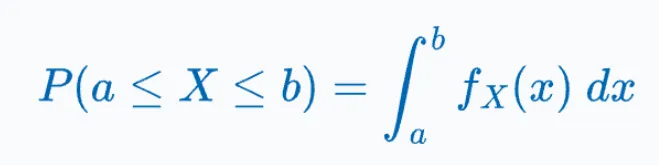
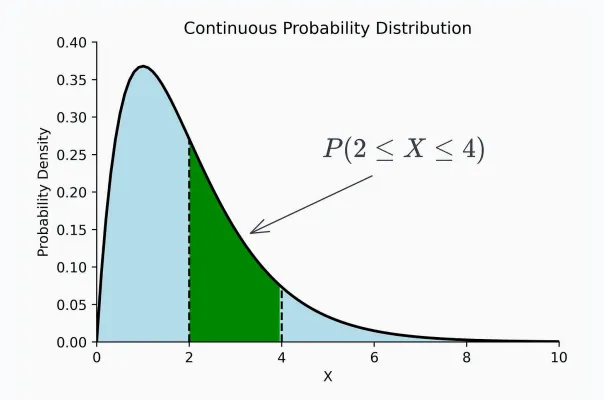
例如，一個人從A點到達B點花費2到4分鐘的概率。

擴展閱讀

似然vs概率

首先讓我們先來看一下概率和似然的區別。

先來看下劍橋詞典給出的解釋。

● Probability: the level of possibility of something happening or being true.

● Likelihood: the chance that something will happen.

這兩個概念非常容易被混淆，在字典中似然被解釋成概率的代名詞。

然而，在統計學中，似然和概率卻有著非常大的區別。

概率通常用于預測一個事件發生的可能性。

例如，擲色子出現偶數的概率，機器學習模型預測輸入是貓的概率。

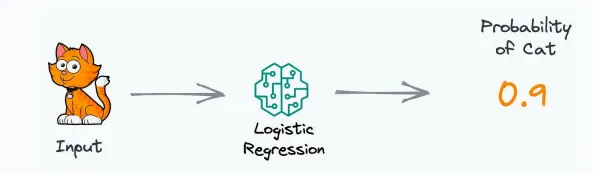
在計算概率時，模型的參數是已知的，并且是可信的。

例如，我們計算拋硬幣正反面的概率時，通常會假設并且相信硬幣是無偏的。

相反，似然用于解釋已經發生的事件。

與概率不同（參數已知，且可信），似然是在已知觀測數據下，幫助我們判定參數是否可靠。

例如，我們將在2D數據上擬合一條直線，參數是斜率m和截距c。

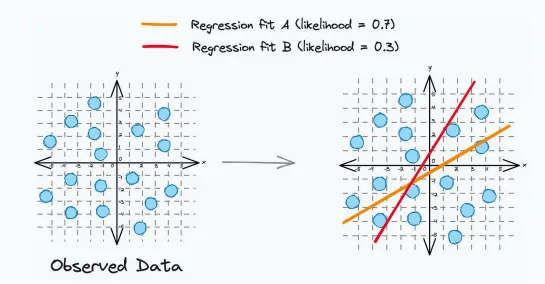
在此，似然被定義為數據點為某些特定參數值提供的支持。

當m=2，c=1時，觀測數據的似然是多少？

當m=3，c=2時，觀測數據的似然是多少？

最大似然估計（MLE）

上面的定義就被應用到了最大似然估計（MLE）中。

MLE用于根據已知的觀測數據來估計模型的參數。其核心思想是，通過尋找使觀測數據最有可能（即似然最大）的參數值。

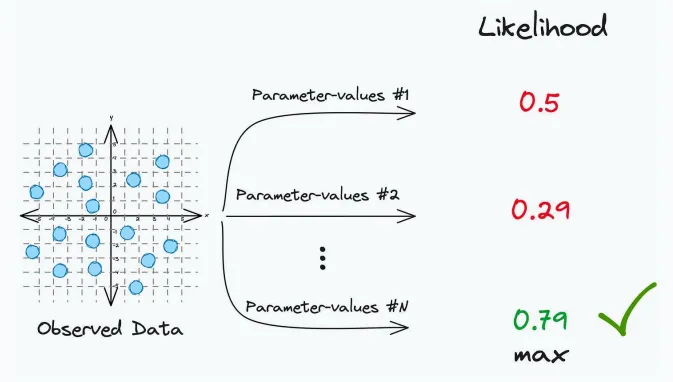
舉個例子。

線性回歸模型的參數有多種求解方法，例如，最小二乘法（OLS），梯度下降法。

今天我們應用概率方法，用最大似然估計（MLE）來求解模型的參數。

1. 定義模型

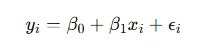
β0、β1為待求解參數。

假設誤差項服從正太分布：

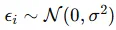
也就是說y服從正太分布：

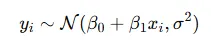
y的概率密度函數為：

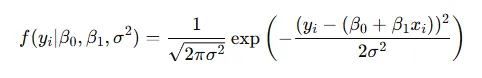
2.構造似然函數

根據獨立同分布假設，整個數據集的似然函數就是各個數據點在PDF中對應概率密度的乘積：

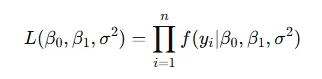
帶入f：

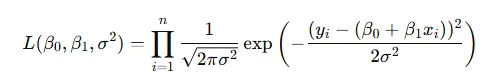
3.取對數似然

根據對數函數的性質，可以將上述似然函數轉換為對數似然函數：

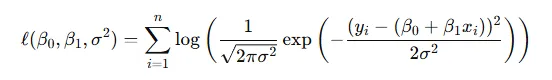
進一步簡化：

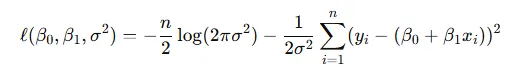
4.最大化似然函數

對數似然函數對參數導數，并令導數為零，得到參數的最大似然估計值：

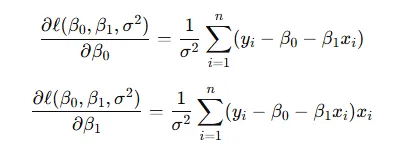
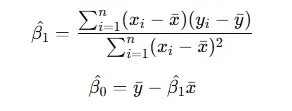
本文轉載自公眾號人工智能大講堂 

原文鏈接：??https://mp.weixin.qq.com/s/vMLzJMoxbCGxiX0PxDT43g???