手動實現一個擴散模型DDPM
擴散模型是目前大部分AIGC生圖模型的基座,其本質是用神經網絡學習從高斯噪聲逐步恢復圖像的過程,本文用python代碼從零開始構建了一個簡單的擴散模型。
一、理論部分
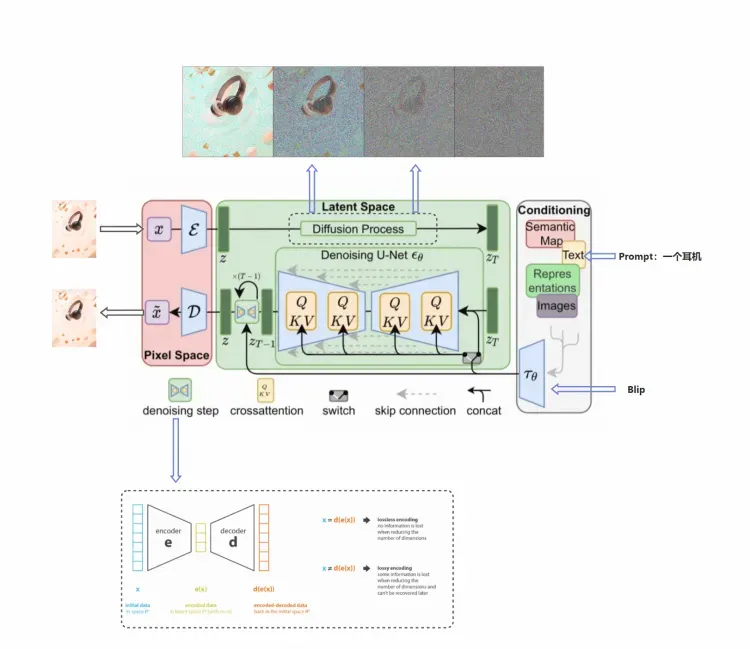
DDPM(Denoising Diffusion Probabilistic Models) 是一種在生成對抗網絡等技術的基礎上發展起來的新型概率模型去噪擴散模型,與其他生成模型(如歸一化流、GANs或VAEs)相比并不是那么復雜,DDPM由兩部分組成:
- 一個固定的前向傳播的過程,它會逐漸將高斯噪聲添加到圖像中,直到最終得到純噪聲
- 一種可學習的反向去噪擴散過程,訓練神經網絡以從純噪聲開始逐漸對圖像進行去噪
前向過程
前向擴散過程,其本質上是一個不斷加噪聲的過程。如下圖所示,在貓的圖片中多次增加高斯噪聲直至圖片變成隨機噪音矩陣。可以看到,對于初始數據,我們設置K步的擴散步數,每一步增加一定的噪聲,如果我們設置的K足夠大,那么我們就能夠將初始數據轉化成隨機噪音矩陣。



具體推理驗證可參考:??http://www.egbenz.com/#/my_article/12??
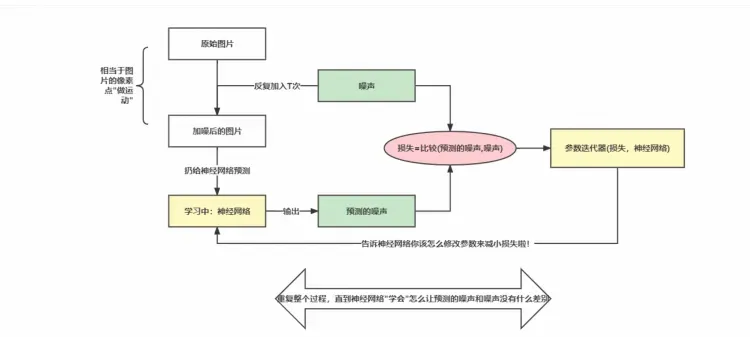
訓練過程
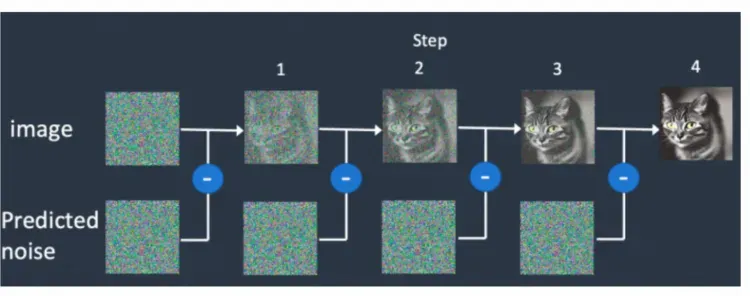
反向生成過程和前向擴散過程相反,是一個不斷去噪的過程。神經網絡從一個隨機高斯噪聲矩陣開始通過擴散模型的Inference過程不斷預測并去除噪聲。
二、實踐部分
環境包
我們將首先安裝并導入所需的庫。
!pip install -q -U einops datasets matplotlib tqdm
import math
from inspect import isfunction
from functools import partial
%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
from einops import rearrange, reduce
from einops.layers.torch import Rearrange
import torch
from torch import nn, einsum
import torch.nn.functional as F加噪聲

下面是一些周期性的函數,這段代碼定義了幾種不同的函數,每個函數都用于計算深度學習中的beta調度(scheduling)。Beta調度主要用于控制噪聲添加的程度,具體代碼如下:
import torch
# cosine_beta_schedule函數用于創建一個余弦退火beta調度。
# 這種調度方法基于余弦函數,并且可以調整隨時間的衰減速率。
def cosine_beta_schedule(timesteps, s=0.008):
steps = timesteps + 1 # 計算總的步數,需要比時間步多一個,以便計算alpha的累積乘積
x = torch.linspace(0, timesteps, steps) # 創建從0到timesteps的均勻分布的張量
# 計算alpha的累積乘積,使用一個余弦變換,并平方來計算當前步的alpha值
alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0] # 歸一化,確保初始值為1
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1]) # 計算每個時間步的beta值
return torch.clip(betas, 0.0001, 0.9999) # 對beta值進行裁剪,避免過大或過小
# linear_beta_schedule函數用于創建一個線性退火beta調度。
# 這意味著beta值將從beta_start線性增加到beta_end。
def linear_beta_schedule(timesteps):
beta_start = 0.0001 # 定義起始beta值
beta_end = 0.02 # 定義結束beta值
return torch.linspace(beta_start, beta_end, timesteps) # 創建一個線性分布的beta值數組
# quadratic_beta_schedule函數用于創建一個二次退火beta調度。
# 這意味著beta值將根據二次函數變化。
def quadratic_beta_schedule(timesteps):
beta_start = 0.0001 # 定義起始beta值
beta_end = 0.02 # 定義結束beta值
# 創建一個線性分布的數組,然后將其平方以生成二次分布,最后再次平方以計算beta值
return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2
# sigmoid_beta_schedule函數用于創建一個sigmoid退火beta調度。
# 這意味著beta值將根據sigmoid函數變化,這是一種常見的激活函數。
def sigmoid_beta_schedule(timesteps):
beta_start = 0.0001 # 定義起始beta值
beta_end = 0.02 # 定義結束beta值
betas = torch.linspace(-6, 6, timesteps) # 創建一個從-6到6的線性分布,用于sigmoid函數的輸入
# 應用sigmoid函數,并根據beta_start和beta_end調整其范圍和位置
return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start
# import torch # 假設在代碼的其他部分已經導入了torch庫
# 定義前向擴散函數
# x_start: 初始數據,例如一批圖像
# t: 擴散的時間步,表示當前的擴散階段
# noise: 可選參數,如果提供,則使用該噪聲數據;否則,將生成新的隨機噪聲
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start) # 如果未提供噪聲,則生成一個與x_start形狀相同的隨機噪聲張量
# 提取對應于時間步t的α的累積乘積的平方根
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
# 提取對應于時間步t的1-α的累積乘積的平方根
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
# 返回前向擴散的結果,該結果是初始數據和噪聲的線性組合
# 系數sqrt_alphas_cumprod_t和sqrt_one_minus_alphas_cumprod_t分別用于縮放初始數據和噪聲
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise 測試如下:
# take time step
for noise in [10,20,40,80 100]:
t = torch.tensor([40])
get_noisy_image(x_start, t)take time step
for noise in [10,20,40,80 100]: t = torch.tensor([40]) get_noisy_image(x_start, t)
核心殘差網絡
下面是殘差網絡的實現代碼,Block 類是一個包含卷積、歸一化、激活函數的標準神經網絡層。ResnetBlock 類構建了一個殘差塊(residual block),這是深度殘差網絡(ResNet)的關鍵特性,它通過學習輸入和輸出的差異來提高網絡性能。在 ResnetBlock 中,可選的 time_emb 參數和內部的 mlp 允許該Block處理與時間相關的特征。
import torch.nn as nn
from einops import rearrange # 假設已經導入了einops庫中的rearrange函數
from torch_utils import exists # 假設已經定義了exists函數,用于檢查對象是否存在
# 定義一個基礎的Block類,該類將作為神經網絡中的一個基本構建模塊
class Block(nn.Module):
def __init__(self, dim, dim_out, groups=8):
super().__init__()
# 一個2D卷積層,卷積核大小為3x3,邊緣填充為1,從輸入維度dim到輸出維度dim_out
self.proj = nn.Conv2d(dim, dim_out, 3, padding=1)
# GroupNorm層用于歸一化,分組數為groups
self.norm = nn.GroupNorm(groups, dim_out)
# 使用SiLU(也稱為Swish)作為激活函數
self.act = nn.SiLU()
def forward(self, x, scale_shift=None):
x = self.proj(x) # 應用卷積操作
x = self.norm(x) # 應用歸一化操作
# 如果scale_shift參數存在,則對歸一化后的數據進行縮放和位移操作
if exists(scale_shift):
scale, shift = scale_shift
x = x * (scale + 1) + shift
x = self.act(x) # 應用激活函數
return x # 返回處理后的數據
# 定義一個ResnetBlock類,用于構建殘差網絡中的基本塊
class ResnetBlock(nn.Module):
"""https://arxiv.org/abs/1512.03385"""
def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8):
super().__init__()
# 如果time_emb_dim存在,定義一個小型的多層感知器(MLP)網絡
self.mlp = (
nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out))
if exists(time_emb_dim)
else None
)
# 定義兩個順序的基礎Block模塊
self.block1 = Block(dim, dim_out, groups=groups)
self.block2 = Block(dim_out, dim_out, groups=groups)
# 如果輸入維度dim和輸出維度dim_out不同,則使用1x1卷積進行維度調整
# 否則使用Identity層(相當于不做任何處理)
self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()
def forward(self, x, time_emb=None):
h = self.block1(x) # 通過第一個Block模塊
# 如果存在時間嵌入向量time_emb且存在mlp模塊,則將其應用到h上
if exists(self.mlp) and exists(time_emb):
time_emb = self.mlp(time_emb) # 通過MLP網絡
# 重整time_emb的形狀以匹配h的形狀,并將結果加到h上
h = rearrange(time_emb, "b c -> b c 1 1") + h
h = self.block2(h) # 通過第二個Block模塊
return h + self.res_conv(x) # 將Block模塊的輸出與調整維度后的原始輸入x相加并返回注意力機制
DDPM的作者把大名鼎鼎的注意力機制加在卷積層之間。注意力機制是Transformer架構的基礎模塊(參考:Vaswani et al., 2017),Transformer在AI各個領域,NLP,CV等等都取得了巨大的成功,這里Phil Wang實現了兩個變種版本,一個是普通的多頭注意力(用在了transformer中),另一種是線性注意力機制(參考:Shen et al.,2018),和普通的注意力在時間和存儲的二次的增長相比,這個版本是線性增長的。
SelfAttention可以將輸入圖像的不同部分(像素或圖像Patch)進行交互,從而實現特征的整合和全局上下文的引入,能夠讓模型建立捕捉圖像全局關系的能力,有助于模型理解不同位置的像素之間的依賴關系,以更好地理解圖像的語義。
在此基礎上,SelfAttention還能減少平移不變性問題,SelfAttention模塊可以在不考慮位置的情況下捕捉特征之間的關系,因此具有一定的平移不變性。
參考:Vaswani et al., 2017 地址:https://arxiv.org/abs/1706.03762
參考:Shen et al.,2018 地址:https://arxiv.org/abs/1812.01243
import torch
from torch import nn
from einops import rearrange
import torch.nn.functional as F
# 定義一個標準的多頭注意力(Multi-Head Attention)機制的類
class Attention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
# 根據維度的倒數平方根來縮放查詢(Query)向量
self.scale = dim_head ** -0.5
# 頭的數量(多頭中的"多")
self.heads = heads
# 計算用于多頭注意力的隱藏層維度
hidden_dim = dim_head * heads
# 定義一個卷積層將輸入的特征映射到QKV(查詢、鍵、值)空間
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
# 定義一個卷積層將多頭注意力的輸出映射回原特征空間
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
# 獲取輸入的批量大小、通道數、高度和寬度
b, c, h, w = x.shape
# 使用to_qkv卷積層得到QKV,并將其分離為三個組件
qkv = self.to_qkv(x).chunk(3, dim=1)
# 將QKV重排并縮放查詢向量
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q * self.scale
# 使用愛因斯坦求和約定計算查詢和鍵之間的相似度得分
sim = einsum("b h d i, b h d j -> b h i j", q, k)
# 從相似度得分中減去最大值以提高數值穩定性
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
# 應用Softmax函數獲取注意力權重
attn = sim.softmax(dim=-1)
# 使用注意力權重對值進行加權
out = einsum("b h i j, b h d j -> b h i d", attn, v)
# 將輸出重新排列回原始的空間形狀
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
# 返回通過輸出卷積層的結果
return self.to_out(out)
# 定義一個線性注意力(Linear Attention)機制的類
class LinearAttention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
# 根據維度的倒數平方根來縮放查詢(Query)向量
self.scale = dim_head ** -0.5
# 頭的數量
self.heads = heads
# 計算用于多頭注意力的隱藏層維度
hidden_dim = dim_head * heads
# 定義一個卷積層將輸入的特征映射到QKV空間
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
# 定義一個順序容器包含卷積層和組歸一化層將輸出映射回原特征空間
self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1),
nn.GroupNorm(1, dim))
def forward(self, x):
# 獲取輸入的批量大小、通道數、高度和寬度
b, c, h, w = x.shape
# 使用to_qkv卷積層得到QKV,并將其分離為三個組件
qkv = self.to_qkv(x).chunk(3, dim=1)
# 將QKV重排,應用Softmax函數并縮放查詢向量
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q.softmax(dim=-2)
k = k.softmax(dim=-1)
q = q * self.scale
# 計算上下文矩陣,是鍵和值的加權組合
context = torch.einsum("b h d n, b h e n -> b h d e", k, v)
# 使用上下文矩陣和查詢計算最終的注意力輸出
out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
# 將輸出重新排列回原始的空間形狀
out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
# 返回經過輸出順序容器處理的結果
return self.to_out(out)位置嵌入
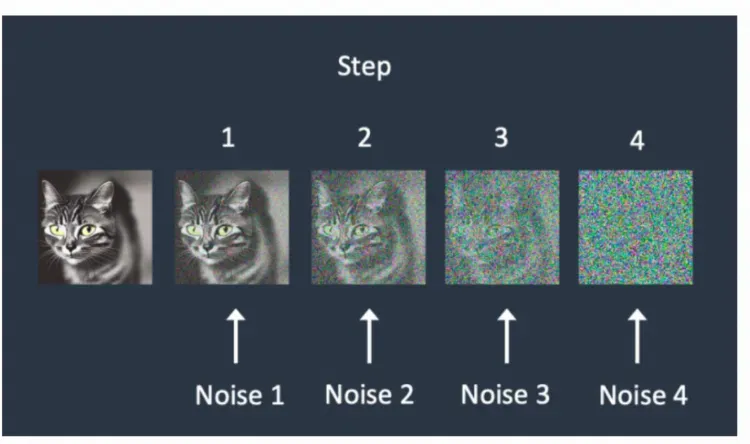
如何讓網絡知道目前處于K的哪一步?可以增加一個Time Embedding(類似于Positional embeddings)進行處理,通過將timestep編碼進網絡中,從而只需要訓練一個共享的U-Net模型,就可以讓網絡知道現在處于哪一步了。
Time Embedding正是輸入到ResNetBlock模塊中,為U-Net引入了時間信息(時間步長T,T的大小代表了噪聲擾動的強度),模擬一個隨時間變化不斷增加不同強度噪聲擾動的過程,讓SD模型能夠更好地理解時間相關性。
同時,在SD模型調用U-Net重復迭代去噪的過程中,我們希望在迭代的早期,能夠先生成整幅圖片的輪廓與邊緣特征,隨著迭代的深入,再補充生成圖片的高頻和細節特征信息。由于在每個ResNetBlock模塊中都有Time Embedding,就能告訴U-Net現在是整個迭代過程的哪一步,并及時控制U-Net夠根據不同的輸入特征和迭代階段而預測不同的噪聲殘差。
從AI繪畫應用視角解釋一下Time Embedding的作用。Time Embedding能夠讓SD模型在生成圖片時考慮時間的影響,使得生成的圖片更具有故事性、情感和沉浸感等藝術效果。并且Time Embedding可以幫助SD模型在不同的時間點將生成的圖片添加完善不同情感和主題的內容,從而增加了AI繪畫的多樣性和表現力。
class SinusoidalPositionEmbeddings(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, time):
device = time.device
half_dim = self.dim // 2
embeddings = math.log(10000) / (half_dim - 1)
embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
embeddings = time[:, None] * embeddings[None, :]
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
return embeddings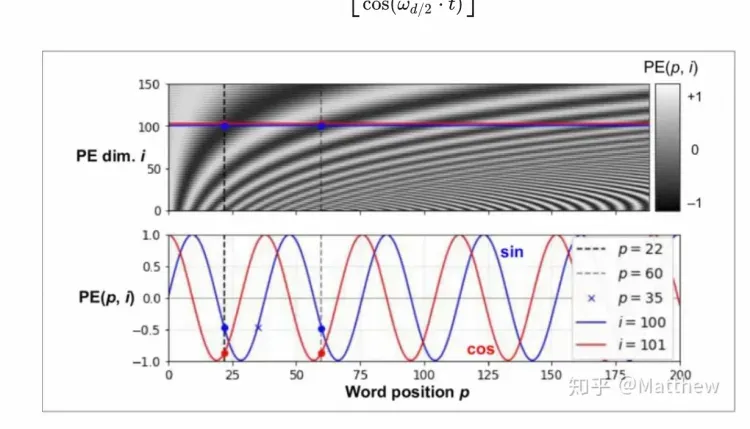

U-net
基于上述定義的DM神經網絡基礎的層和模塊,現在是時候把他組裝拼接起來了:
- 神經網絡接受一批如下shape的噪聲圖像輸入(batch_size, num_channels, height, width) 同時接受這批噪聲水平,shape=(batch_size, 1)。返回一個張量,shape = (batch_size, num_channels, height, width)
按照如下步驟構建這個網絡:
- 首先,對噪聲圖像進行卷積處理,對噪聲水平進行進行位置編碼(embedding)
- 然后,進入一個序列的下采樣階段,每個下采樣階段由兩個ResNet/ConvNeXT模塊+分組歸一化+注意力模塊+殘差鏈接+下采樣完成。
- 在網絡的中間層,再一次用ResNet/ConvNeXT模塊,中間穿插著注意力模塊(Attention)。
- 下一個階段,則是序列構成的上采樣階段,每個上采樣階段由兩個ResNet/ConvNeXT模塊+分組歸一化+注意力模塊+殘差鏈接+上采樣完成。
- 最后,一個ResNet/ConvNeXT模塊后面跟著一個卷積層。
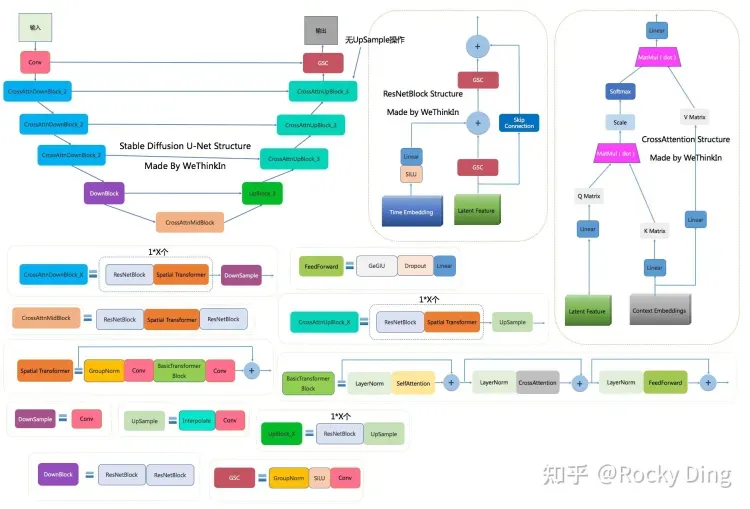
class Unet(nn.Module):
# 初始化函數,定義U-Net網絡的結構和參數
def __init__(
self,
dim, # 基本隱藏層維度
init_dim=None, # 初始層維度,如果未提供則會根據dim計算得出
out_dim=None, # 輸出維度,如果未提供則默認為輸入圖像的通道數
dim_mults=(1, 2, 4, 8), # 控制每個階段隱藏層維度倍增的倍數
channels=3, # 輸入圖像的通道數,默認為3
with_time_emb=True, # 是否使用時間嵌入,這對于某些生成模型可能是必要的
resnet_block_groups=8, # ResNet塊中的組數
use_cnotallow=True, # 是否使用ConvNeXt塊而不是ResNet塊
convnext_mult=2, # ConvNeXt塊的維度倍增因子
):
super().__init__() # 調用父類構造函數
# 確定各層維度
self.channels = channels
init_dim = default(init_dim, dim // 3 * 2) # 設置或計算初始層維度
self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3) # 初始卷積層,使用7x7卷積核和padding
dims = [init_dim, *map(lambda m: dim * m, dim_mults)] # 計算每個階段的維度
in_out = list(zip(dims[:-1], dims[1:])) # 創建輸入輸出維度對
# 根據use_convnext選擇塊類
if use_convnext:
block_klass = partial(ConvNextBlock, mult=convnext_mult)
else:
block_klass = partial(ResnetBlock, groups=resnet_block_groups)
# 時間嵌入層
if with_time_emb:
time_dim = dim * 4 # 時間嵌入的維度
self.time_mlp = nn.Sequential( # 時間嵌入的多層感知機
SinusoidalPositionEmbeddings(dim), # 正弦位置嵌入
nn.Linear(dim, time_dim), # 線性變換
nn.GELU(), # GELU激活函數
nn.Linear(time_dim, time_dim), # 再一次線性變換
)
else:
time_dim = None
self.time_mlp = None
# 下采樣層
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out) # 解析的層數
# 構建下采樣模塊
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1) # 是否為最后一層
self.downs.append( # 添加下采樣塊
nn.ModuleList(
[
block_klass(dim_in, dim_out, time_emb_dim=time_dim), # 卷積塊
block_klass(dim_out, dim_out, time_emb_dim=time_dim), # 卷積塊
Residual(PreNorm(dim_out, LinearAttention(dim_out))), # 殘差連接和注意力模塊
Downsample(dim_out) if not is_last else nn.Identity(), # 下采樣或恒等映射
]
)
)
# 中間層(瓶頸層)
mid_dim = dims[-1]
# 中間層(瓶頸層)
# 第一個中間卷積塊
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
# 中間層的注意力模塊
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
# 第二個中間卷積塊
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
# 構建上采樣模塊
for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
is_last = ind >= (num_resolutions - 1) # 是否是最后一次上采樣,減2是因為我們需要留出一個輸出層
self.ups.append(
nn.ModuleList(
[
# 卷積塊,這里輸入維度翻倍是因為上采樣過程中會與編碼器階段的相應層進行拼接
block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim),
# 卷積塊
block_klass(dim_in, dim_in, time_emb_dim=time_dim),
# 殘差和注意力模塊
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
# 上采樣或恒等映射
Upsample(dim_in) if not is_last else nn.Identity(),
]
)
)
# 設置或計算輸出維度,如果未提供則默認為輸入圖像的通道數
out_dim = default(out_dim, channels)
# 最后的卷積層,將輸出維度變換到期望的輸出維度
self.final_conv = nn.Sequential(
block_klass(dim, dim), # 卷積塊
nn.Conv2d(dim, out_dim, 1) # 1x1卷積,用于輸出維度變換
)
# 前向傳播函數
def forward(self, x, time):
# 初始卷積層
x = self.init_conv(x)
# 如果存在時間嵌入層,則將時間編碼
t = self.time_mlp(time) if exists(self.time_mlp) else None
# 用于存儲各個階段的特征圖
h = []
# 下采樣過程
for block1, block2, attn, downsample in self.downs:
x = block1(x, t) # 應用卷積塊
x = block2(x, t) # 應用卷積塊
x = attn(x) # 應用注意力模塊
h.append(x) # 存儲特征圖以便后續的拼接
x = downsample(x) # 應用下采樣或恒等映射
# 中間層或瓶頸層
x = self.mid_block1(x, t) # 第一個中間卷積塊
x = self.mid_attn(x) # 中間層的注意力模塊
x = self.mid_block2(x, t) # 第二個中間卷積塊
# 上采樣過程
for block1, block2, attn, upsample in self.ups:
# 拼接特征圖和對應的編碼器階段的特征圖
x = torch.cat((x, h.pop()), dim=1)
x = block1(x, t) # 應用卷積塊
x = block2(x, t) # 應用卷積塊
x = attn(x) # 應用注意力模塊
x = upsample(x) # 應用上采樣或恒等映射
# 最后的輸出層,輸出最終的特征圖或圖像
return self.final_conv(x)損失函數
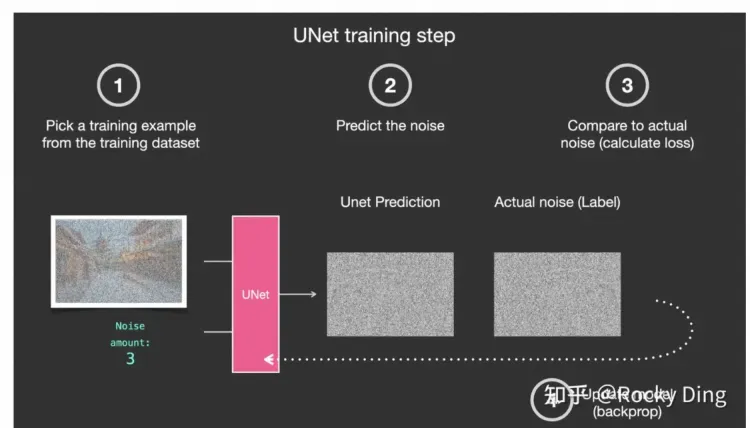
下面這段代碼是為擴散模型中的去噪模型定義的損失函數。它計算由去噪模型預測的噪聲和實際加入的噪聲之間的差異。該函數支持不同類型的損失,包括L1損失、均方誤差損失(L2損失)和Huber損失。選擇適當的損失函數可以幫助模型更好地學習如何預測和去除生成數據中的噪聲。
import torch
import torch.nn.functional as F
# 定義損失函數,它評估去噪模型的性能
def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
if noise is None:
noise = torch.randn_like(x_start) # 如果未提供噪聲,則生成一個與x_start形狀相同的隨機噪聲張量
# 使用q_sample函數生成帶有噪聲的數據x_noisy,這模擬了擴散模型的前向過程
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# 使用去噪模型對噪聲數據x_noisy進行預測,試圖恢復加入的噪聲
predicted_noise = denoise_model(x_noisy, t)
# 根據指定的損失類型計算損失
if loss_type == 'l1': # 如果損失類型為L1損失
loss = F.l1_loss(noise, predicted_noise) # 使用L1損失函數計算真實噪聲和預測噪聲之間的差異
elif loss_type == 'l2': # 如果損失類型為L2損失(均方誤差損失)
loss = F.mse_loss(noise, predicted_noise) # 使用均方誤差損失函數計算真實噪聲和預測噪聲之間的差異
elif loss_type == "huber": # 如果損失類型為Huber損失
loss = F.smooth_l1_loss(noise, predicted_noise) # 使用Huber損失函數,這是L1和L2損失的結合,對異常值不那么敏感
else:
raise NotImplementedError() # 如果指定了未實現的損失類型,則拋出異常
return loss # 返回計算得到的損失值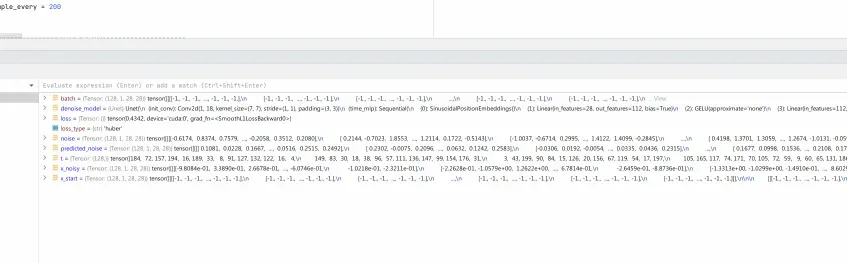
開始訓練
if __name__=="__main__":
for epoch in range(epochs):
for step, batch in tqdm(enumerate(dataloader), desc='Training'):
optimizer.zero_grad()
batch = batch[0]
batch_size = batch.shape[0]
batch = batch.to(device)
# 國內版啟用這段,注釋上面兩行
# batch_size = batch[0].shape[0]
# batch = batch[0].to(device)
# Algorithm 1 line 3: sample t uniformally for every example in the batch
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t, loss_type="huber")
if step % 50 == 0:
print("Loss:", loss.item())
loss.backward()
optimizer.step()
# save generated images
if step != 0 and step % save_and_sample_every == 0:
milestone = step // save_and_sample_every
batches = num_to_groups(4, batch_size)
all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches))
all_images = torch.cat(all_images_list, dim=0)
all_images = (all_images + 1) * 0.5
# save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)
currentDateAndTime = datetime.now()
torch.save(model,f"train.pt")推理結果
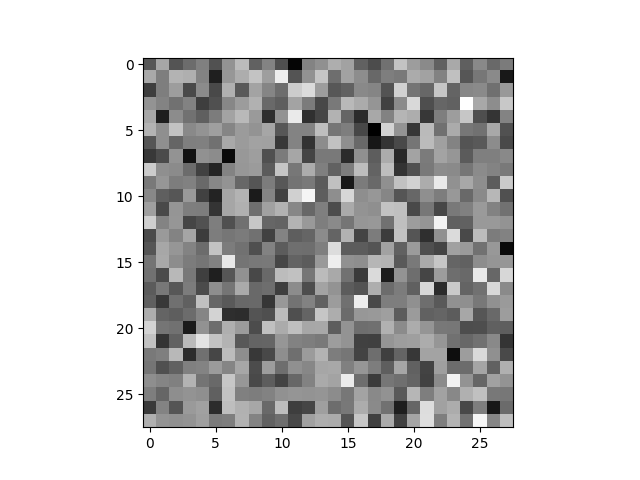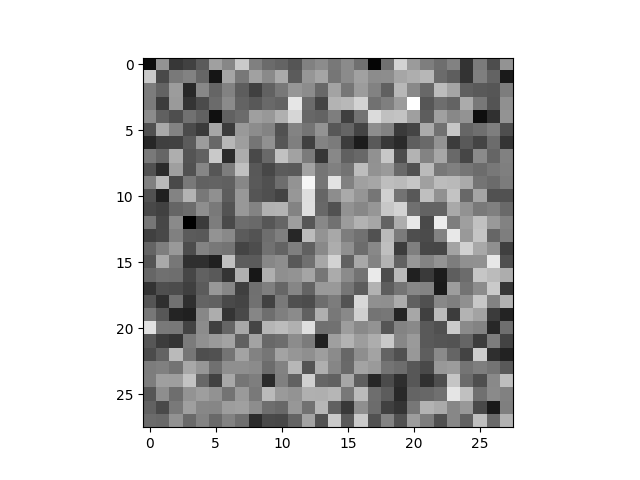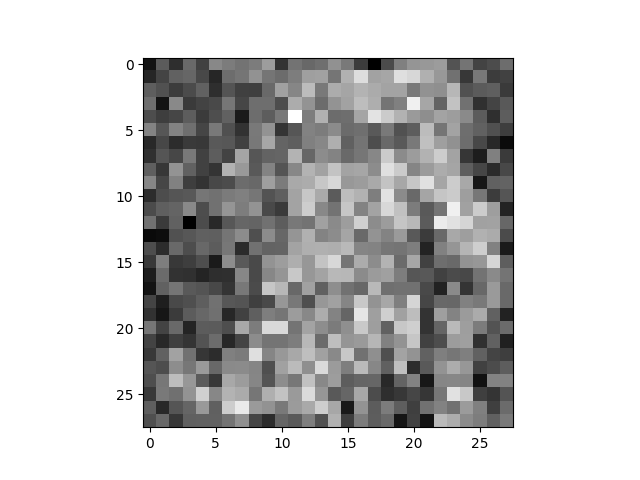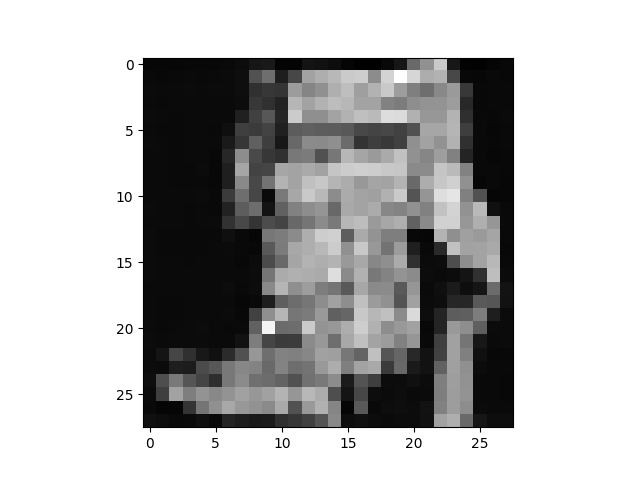
三、參考文獻
- 深入學習:Diffusion Model 原理解析(地址:http://www.egbenz.com/#/my_article/12)
- 【一個本子】Diffusion Model 原理詳解(地址:https://zhuanlan.zhihu.com/p/582072317)
- 深入淺出擴散模型(Diffusion Model)系列:基石DDPM(模型架構篇),最詳細的DDPM架構圖解(地址:https://zhuanlan.zhihu.com/p/637815071)
- 一文讀懂Transformer模型的位置編碼(地址:https://zhuanlan.zhihu.com/p/637815071
- ??https://zhuanlan.zhihu.com/p/632809634??
四、團隊介紹
我們是淘天集團業務技術線的手貓營銷&導購團隊,專注于在手機天貓平臺上探索創新商業化,我們依托淘天集團強大的互聯網背景,致力于為手機天貓平臺提供效率高、創新性強的技術支持。
我們的隊員們來自各種營銷和導購領域,擁有豐富的經驗。通過不斷地技術探索和商業創新,我們改善了用戶的體驗,并提升了平臺的運營效率。
我們的團隊持續不懈地探索和提升技術能力,堅持“技術領先、用戶至上”,為手機天貓的導購場景和商業發展做出了顯著貢獻。
本文轉載自大淘寶技術,作者:修尋


















