“ 向量是大模型技術的基礎數據格式，也是用來描述語義關系的核心數學模型 ”

大模型是基于向量作為基礎數據格式，這是一個客觀存在的事實；但在此之前一直沒有深入思考過向量這個問題；最近幾天在搞向量數據庫的時候，才突然發現向量遠遠沒有想的那么簡單。

思考一個簡單的問題，向量數據庫實現的原理是什么？ 

由向量數據庫引起的思考

在上面的問題中，向量數據庫的實現原理，說到這個可能很多人會覺得這個問題太復雜；那么就換一種簡單的問法，向量檢索的原理是什么？

學過中學數學的應該都知道，向量是一種具有大小和方向的量；直觀體現就是在平面坐標系中的一個黑色箭頭。

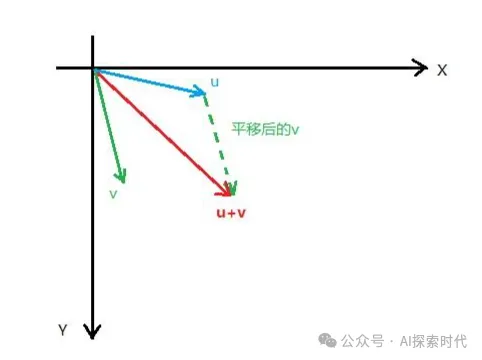
但那時所學的向量屬于基礎的數學概念，和今天所講的大模型使用的向量還不是一回事；一般說到向量，我們指的都是空間向量，也就是能在坐標系中畫出來，能讓我們直觀看到的類似空間幾何的東西。

但大模型所使用的向量是一種數學概念上的向量，而不是我們所認為的空間向量；比如說320維的向量，誰知道320維是什么樣的，四維空間到現在我們還無法想象呢。

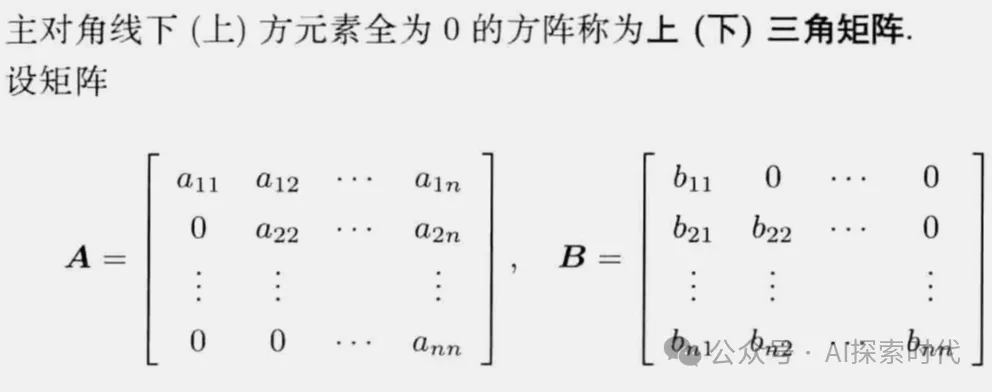
大模型所使用的向量，在數學上是通過矩陣來表示的一種數學結構；在編程技術中就是數據結構中的多維數組，或者叫矩陣。

在前面的文章中有說過，之前的檢索都是通過字符匹配的方式來實現；但大模型作為人工智能技術的實現方式之一，需要做的不僅僅只是字符匹配，還需要有語義關聯。

比如說，我好餓，我想吃飯；這是一句有實際語義的一句話；而如果是一篇文章，一本書，那都是具有實際語義的話；而且同樣的話，在不同的語境下會有不同的意義；因此，就需要一種方式來表達或者說描述語義之間的關系，而最終選擇的就是向量。

那向量在大模型中的意義是什么？以及其是怎么實現的？

向量是描述大模型系統的一個數學結構，由于大模型的復雜度，因為就需要有一種數學結構去描述這種復雜關系；而向量由于其具有高維性質，因為就剛好可以用來描述復雜的模型關系。比如常見的歐式距離以及余弦相似度，經常被用來計算向量之間的關系，也就是文本(包括其它模態的數據)的語義關系。

而在大模型的發展與具體應用中，大模型所支持的數據格式也越來越多；比如說隨著多模態大模型的興起，大模型所面臨的場景越來越復雜，難度也同樣呈幾何度上升。

而怎么對這種多模態數據進行統一處理，同樣需要一種基礎的數學結構；而向量剛好能滿足這個要求；原因就在于，高維向量的復雜性導致其能涵蓋各種復雜的任務場景，并且能夠通過數值計算的方式來處理這些數據。

如果從向量的角度來理解大模型訓練和微調，那么大模型的訓練和微調是在做什么？ 

大模型的訓練和微調就是通過一種數據模型，把輸入到模型中的訓練數據，使用向量去描述其關系，然后根據損失函數的誤差，不斷的去調整其向量關系的值；最后使得這個值達到最優解；然后把模型的計算參數(大模型的參數)保存下來。

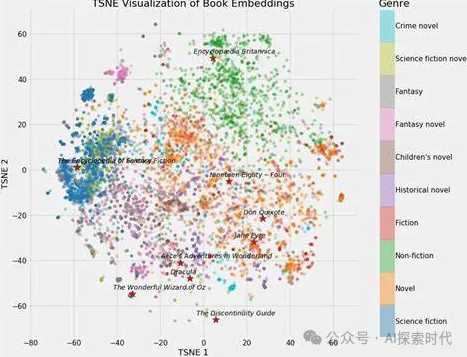
所以，在大模型訓練完成之后，就可以通過保存下來的參數來描述新的輸入數據；然后根據新數據的要求來生成其向量關系最近的新內容。

從這一點來看，所謂的大模型技術就是尋找一種通用的數學模型；去計算不同模態數據的數學關系；而描述這種數學關系的數學類型就是向量。

所以，如果從這一點進行反推，在未來有一種數學模型能夠完全模擬人腦的運作方式；那么就可以用一種數據格式(如向量)來描述大腦的思維過程，實現最終的人工智能。

原文鏈接：??https://mp.weixin.qq.com/s/gdQtsJN13gQ-caJlTUFzRg??