人工智能小白到高手:什么是損失函數
在機器學習中,損失函數是用來衡量模型預測值與真實值之間差距的一個函數。它在模型訓練過程中起著至關重要的作用,因為通過最小化損失函數,模型能夠調整其參數,從而使得預測結果越來越接近真實值。
為了幫助理解這一點,我們將以均方誤差(MSE)為例,詳細講解什么是損失函數,以及它在實際應用中的作用。
什么是損失函數?
損失函數是一個用于評估模型預測準確性的數學函數。具體來說,損失函數通過對比模型的預測值與真實值,計算出一個數值(損失),這個數值代表了模型預測的誤差。
如果損失較大,意味著模型的預測值與真實值相差較遠;如果損失較小,說明模型的預測已經較為精確。
在一個預測問題中,假設我們有:

在下圖中,您可以將損失可視化為從數據點指向模型的箭頭。箭頭表示模型的預測結果與實際值之間的差距。
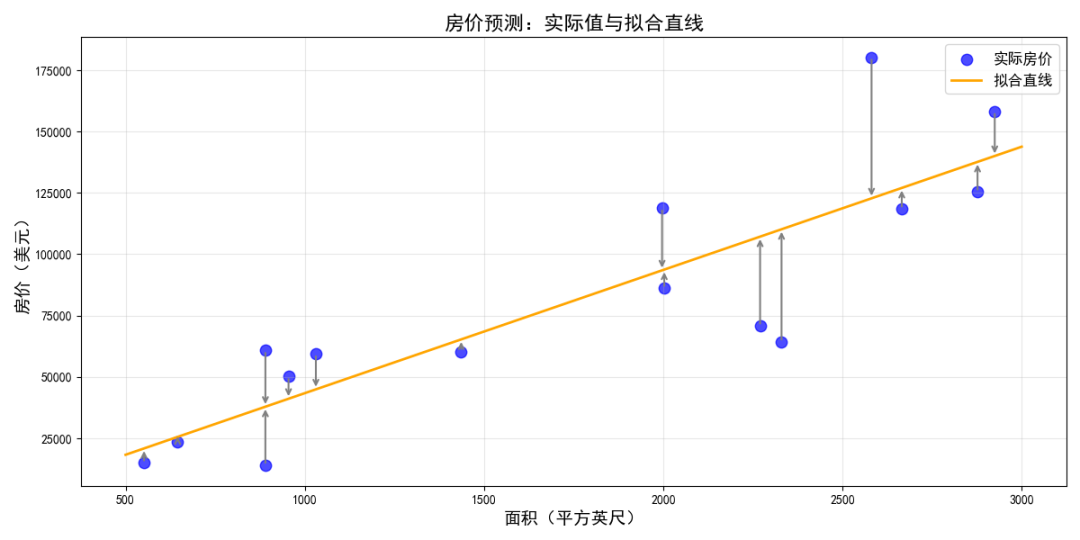
在統計學和機器學習中,損失函數用于衡量預測值與實際值之間的差異。損失函數側重于值之間的距離,而不是方向。
例如,如果模型預測值為 2,但實際值為 5,我們并不關心損失為負值 ?3(2?5=?3)。我們關心的是這兩個值之間的距離為 3。
因此,所有用于計算損失的方法都會移除符號。
移除此符號的兩種最常用方法如下:
- 計算實際值與預測值之間的差值的絕對值。
- 將實際值與預測值之間的差值平方。
均方誤差(MSE)
以回歸任務為例,均方誤差(MSE)是最常見的損失函數之一。
它衡量的是預測值與真實值之間差距的平方的平均值。
均方誤差的優點是,它對大誤差非常敏感,因此可以較好地懲罰那些錯誤較大的預測。MSE是連續型數值任務中常用的損失函數,尤其在模型希望盡量減少預測誤差時特別有效。

為什么需要損失函數?
損失函數的作用可以通過一個簡單的例子來理解。假設我們正在使用線性回歸模型來預測房價,給定某些特征(如面積),模型預測出一個價格,而實際的房價是已知的。
損失函數將計算預測值與真實值之間的差距,具體來說,均方誤差(MSE)將計算每個預測值與真實值之間的差異,然后求出這些差異的平方和的平均值。
通過最小化這個損失函數,模型能夠學習到如何調整其參數,使得預測的房價盡可能接近實際房價。
例如,如果模型的預測差異過大(例如,預測的價格比實際價格高出很多),均方誤差就會較大,模型將意識到它需要進行調整,以減少這種差距。
如何使用損失函數進行優化?
訓練機器學習模型時,我們的目標是最小化損失函數。最常見的方法是使用梯度下降算法。梯度下降通過不斷調整模型的參數,使得損失函數的值逐步減小,從而提升模型的預測能力。
在均方誤差的情況下,我們通過計算損失函數對每個模型參數的梯度(即偏導數),來決定如何調整參數。通過反復進行這一過程,損失函數的值會逐漸減少,模型的預測能力也會逐步增強。
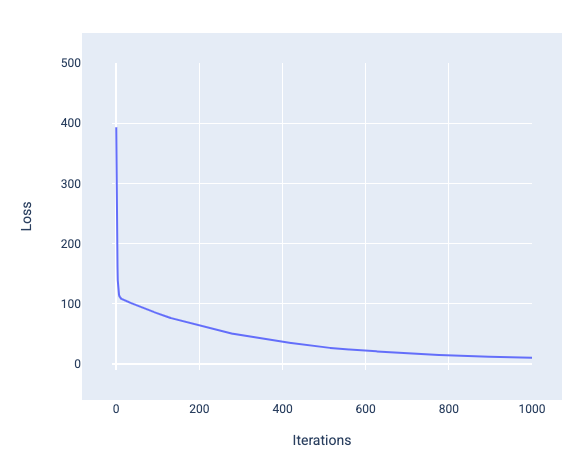
損失曲線,顯示模型在第 1000 次迭代左右收斂。
損失函數的選擇與優化
選擇合適的損失函數是成功訓練模型的關鍵。不同任務可能需要不同的損失函數。
例如,在回歸任務中,均方誤差(MSE)是一種常用的選擇,但在一些特定場景下,如數據中包含大量異常值時,可能需要使用其他損失函數,如平均絕對誤差(MAE)或者Huber損失,它們對異常值更為魯棒。
此外,損失函數的優化也很重要。在使用MSE時,確保數據進行適當的歸一化或標準化,以防止過大的輸入值導致訓練不穩定。合理的學習率選擇、優化器的使用(如Adam或SGD)等因素,也都將影響損失函數的最小化過程。
總結
通過均方誤差(MSE)這一具體例子,了解了什么是損失函數,損失函數如何在機器學習模型中評估預測的準確性,并推動模型優化。
損失函數通過量化模型的預測誤差,為模型提供了學習的反饋,幫助模型在訓練過程中逐步調整參數以達到更好的預測效果。理解損失函數的本質和應用,對于構建有效的機器學習模型至關重要。
本文轉載自 ??AI取經路??,作者: AI取經路

















