神經網絡之損失函數與優化函數——梯度下降 原創
“ 損失函數和梯度下降是神經網絡中僅次于神經網絡模型本身的兩個函數,甚至神經網絡模型的性能就是由其所決定的 ”
今天我們來介紹一下神經網絡模型中非常重要的兩個知識點,損失函數與優化函數。
了解過神經網絡模型基礎運作流程的應該都知道這兩個重要函數,可以說一個神經網絡設計的怎么樣是一方面,但怎么讓神經網絡表現更好,就看這兩個函數的質量了。
損失函數與優化函數??
神經網絡訓練流程
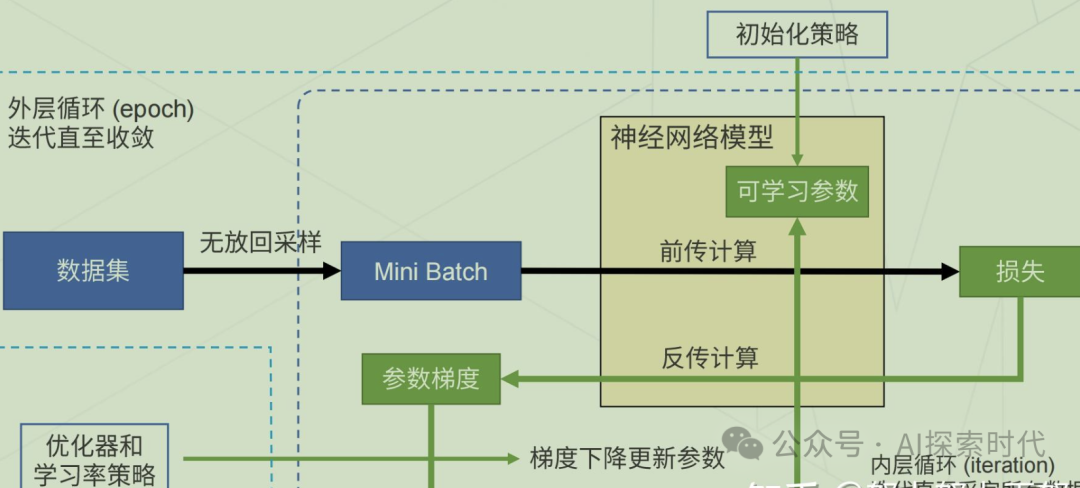
在現有的神經網絡體系中,神經網絡的基本運作模式是,根據需求設計完成神經網絡結構之后;輸入待訓練數據,然后神經網絡就可以通過損失函數計算模型的擬合誤差,然后通過反向傳播的方式使用優化函數來優化模型參數,最終達到最優解——可能只是理論最優解不是實際最優解。???
基本流程如下圖所示:??
損失函數
思考一個問題,損失函數的作用是什么?以及它基本理論是什么樣的? ??????????
從字面來理解,損失函數就是用來計算損失的;但它具體的原理是什么呢? ????????????
在神經網絡中,數據的基本格式是向量;而向量是有大小和方向的量,因此就可以用向量來表示數據之間的關系——也就是相似度。??????
以監督學習圖像處理為例,給你一堆貓或狗的照片,然后把貓和狗單獨放到不同的目錄下,也就是貓一個目錄,狗一個目錄;這時把貓和狗以及他們的標簽——也就是目錄名稱,轉化為向量結構之后;表示貓的向量和表示狗的向量會占據不同的向量空間,而表示不同貓的向量會離的近一點;同樣表示狗的向量也會離的近一點,這種表示方式就叫做歐式距離。????????????????????????
以生活中的分類問題舉例,比如老師在講臺上寫兩個標簽,一個男同學,一個女同學;然后說男同學站男同學標簽下,女同學站女同學標簽下;???????????????????????????????????????????
?監督學習也是同樣的道理,貓狗的標簽(目錄)就是告訴神經網絡模型,這個是貓,那個是狗;然后讓神經網絡模型自己去根據特征讓表示貓的向量和表示狗的向量,盡量靠近貓標簽和狗標簽。?
無監督學習的基礎理論和監督學習基本類似,只不過不會告訴神經網絡貓和狗的標簽;而是讓神經網絡自己去根據貓狗的特征去區分,雖然區分的結果可能是錯的。
但想法雖然很美好,現實卻很殘酷;未經過訓練的神經網絡模型就像幼兒園的小孩子一樣,雖然你說了,他也聽了,但他做的都是錯的;但怎么衡量這個錯誤的大小呢 ???????????
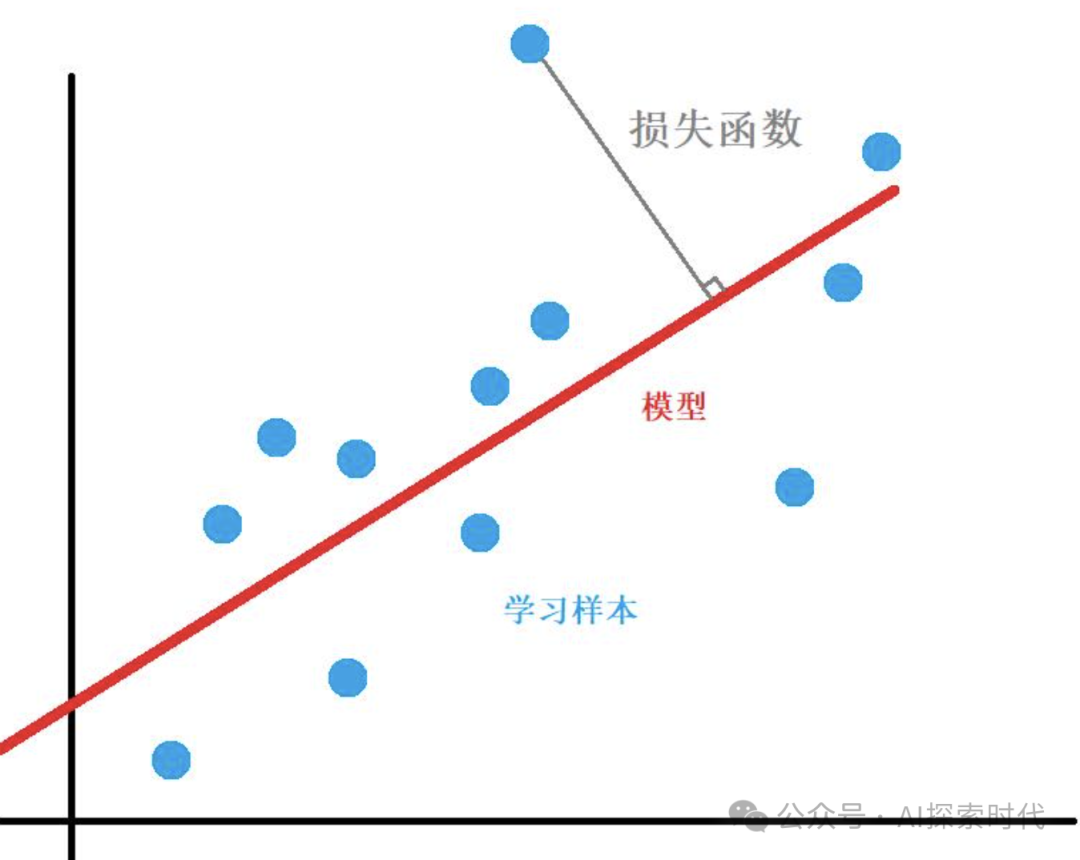
這就是損失函數的作用,通過計算神經網絡給的貓狗向量與真實標簽之間的誤差,來告訴神經網絡你這個搞錯了,再想想辦法;然后神經網絡就會進行新一輪的計算,只不過在從新訓練之前會先進行參數調優,也就是優化函數。???
數學模型如下圖所示:
優化函數
優化函數的作用就是告訴神經網絡模型,你剛剛算的誤差太大了,現在去調整一下你的參數然后從新計算。
但是這里就有一個問題,神經網絡怎么知道自己應該怎么調優?總要有一個具體的解決方法或者說算法吧。??????????
這時優化函數的經典實現——梯度下降的作用就體現了;實現優化函數的方式有多種,但使用最多影響力最大的就是梯度下降算法。?
什么是梯度下降算法?
想明白什么是梯度下降,首先你要明白什么是梯度;假如某一天你和朋友等山的時候遇到意外傷害,這時你的所有通訊設施都無法使用;必須有一個人下山去通知救援隊來救你的隊友。這時你需要找一個在保證安全的前提下,能最快下山的路徑?這時你應該怎么辦?
ok, 先思考一下下山有哪些途徑? ?
1. 找一條人工修好的山路下山,一般是上來的路,也就是原路返回
2. 找一些山間小道,這條路可能會比較難走,但速度會比走修好的山路更快
3. 到懸崖邊,直接跳下去,這是下山最快的一種方式,但結果可能就是直接死亡;這時下山就沒了意義。?????
因此,一般情況下大家應該會選擇第二種方式下山;因為它能在保證盡量安全的前提下,以最快的速度下山。???????
但是同樣,這樣的山路會比第一種的山路要更難走,因為它坡度更大,更陡峭;其實,我們就可以把這個山的坡度理解成梯度。??????????????
簡單來說,所謂的梯度就是衡量某種事物的變化率,但畢竟梯度只是我們想出來的一個東西;我們需要把梯度構建成一個數學模型,這樣我們才能解決它;
而從數學的角度來說梯度其實就是導數問題。導數就是用來衡量函數在某一個點附近的變化率;因此,所謂的梯度問題就是導數問題。只不過真實的神經網絡模型中,梯度下降會更復雜,比如與向量相結合,以及偏導數,方向導數等等。????????????????
如下圖所示:
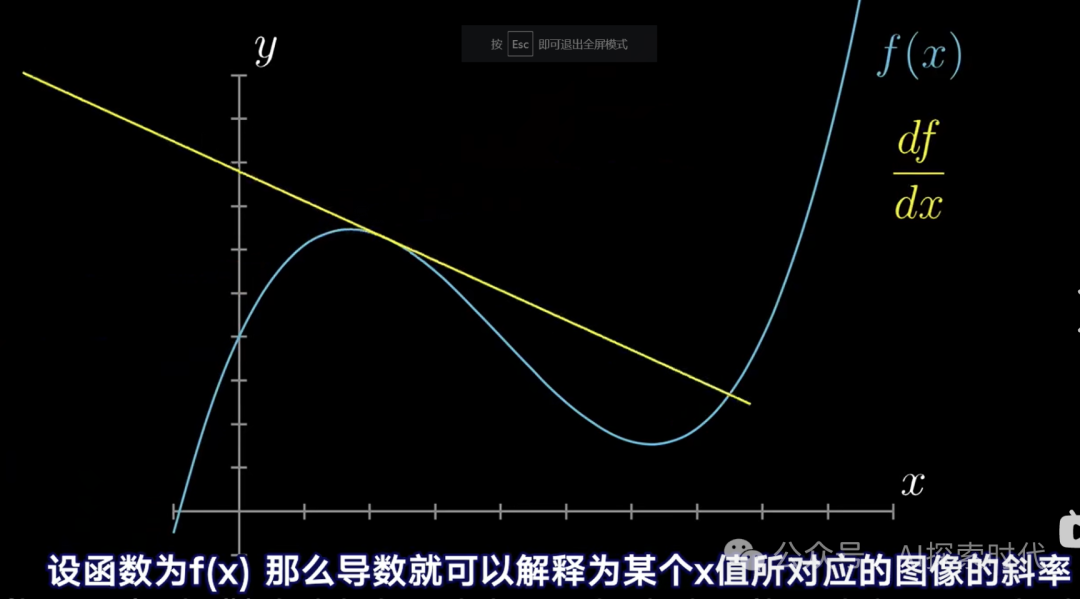
但為什么梯度下降就可以優化損失函數計算的誤差?或者說為什么導數就可以解決損失函數的誤差?
之所以導數能解決損失函數的誤差問題,主要原因就在于,數學追求的一種完美曲線(直線),雖然這個曲線不是一般意義上的水平直線,但它依然是一個連續曲線。???????????????????
而在數學中,通過導數或者多階導數就可以求出損失函數在最小值時,自變量x的取值,也就是極值問題。如下圖所示,關于導數的求值問題。??????????????????????
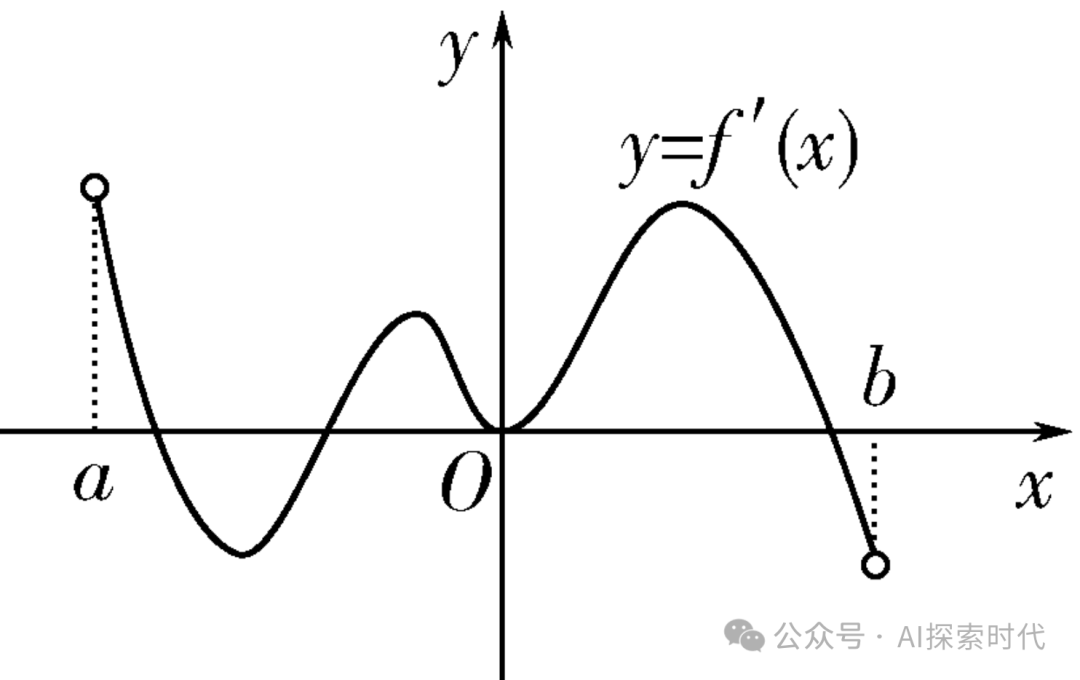
而通過這種方式,損失函數就可以找到其極值點,雖然可能并不是最小值或最大值,原因就在于不同的函數在一定的范圍內可能存在多個極值點;這也是為什么前面說,神經網絡最終得到的最優解只是理論上的最優解,可能并不是實際上的最優解。??????
那么現在應該明白為什么優化函數使用梯度下降算法了吧????????????
原因就在于優化函數會讓損失函數在極值點附近不斷的去測試,然后找到極值;因為,損失函數不能像我們人類一樣,直接畫個圖看一下極值點在哪里,因此損失函數并不知道其極值點在哪里,只能不斷的去計算才能獲得結果。????????
學習率和步長
而關于梯度下降的問題,神經網絡還有兩個超參數,學習率和步長;步長理解比較簡單;以上圖導數求極值為例,如果損失函數想求最小值,但它的起始點是a點,但它的最小值點是b點;如果要在a和b之間一個點一個點的實,那么效率也太低了。因此步長就可以調大一點,第一次在a點,第二次就可以跳到第一個極小值點附近,也就是a和o點之間的最低點;第三次到y所在的最高點,第四次就可以到b所在的最小值點。???????????????????????????????????????????????????
但從上圖也可以看出,如果按照這種步長,損失函數會錯過兩個極大值和一個極小值點;這就可能會產生梯度消失或者梯度爆炸的問題。步長太大可能會導致梯度消失,而步長太小又可能會導致收斂過慢,訓練時間和成本大大增加。?????????????????
而學習率是直接影響步長的參數,很多時候有些人也會把學習率和步長當作是一個東西。??????
這也是為什么在模型訓練中,需要根據不同的模型和場景設置不同的超參數的原因。
本文轉載自公眾號AI探索時代 作者:DFires

















