配置不同的學習率,LoRA還能再漲一點?
LoRA(Low-Rank Adaptation)是當前 LLM 的參數高效微調手段之一,此前我們在《梯度視角下的LoRA:簡介、分析、猜測及推廣》也有過簡單討論。這篇文章我們來學習 LoRA 的一個新結論:
給 LoRA 的兩個矩陣分配不同的學習率,LoRA 的效果還能進一步提升。
該結論出自最近的論文《LoRA+: Efficient Low Rank Adaptation of Large Models》[1](下稱“LoRA+”)。咋看之下,該結論似乎沒有什么特別的,因為配置不同的學習率相當于引入了新的超參數,通常來說只要引入并精調超參數都會有提升。
“LoRA+”的特別之處在于,它從理論角度肯定了這個必要性,并且斷定最優解必然是右矩陣的學習率大于左矩陣的學習率。簡而言之,“LoRA+”稱得上是理論指導訓練并且在實踐中確實有效的經典例子,值得仔細學習一番。

結論簡析

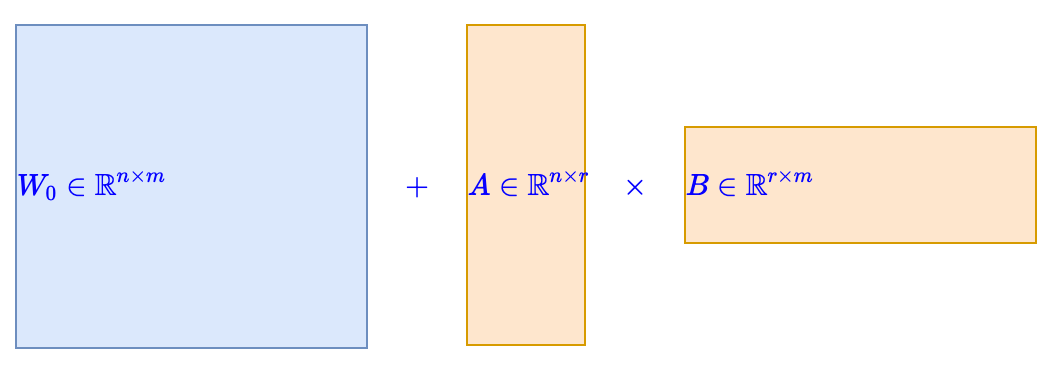

“LoRA+”的結論是:為了使 LoRA 的效果盡可能接近最優,權重 B 的學習率應該要大于權重A的學習率。
注意,為了使初始模型等價于原始預訓練模型,LoRA 通常會將 A,B 之一全零初始化。筆者一開始以為,該結論是由于全零初始化導致的,所以應該依賴于全零初始化的位置,但仔細閱讀后發現,“LoRA+”所聲稱的結論跟全零初始化無關,也就是說,表面上 A,B 是對稱的,但實際上它們有著固有的不對稱性,以至于不管選擇 A 還是 B 來全零初始化,結論都是 B 的學習率要大于 A。這就有意思起來了。
不得不說。“LoRA+”原文的推導寫得相當讓人費解,下面筆者盡量用自己的思路來完成推導。大體上,它基于兩點假設:1. 數值穩定:模型每一層的輸出值都應該是數值穩定的,跟網絡寬度無關;2. 貢獻相當:為了使 LoRA 最優,A,B 兩個矩陣對效果應該有同等程度的貢獻。接下來我們逐一分析并量化這兩點假設。

數值穩定


單看前向傳播來說,XA 的數值穩定性確實不是必要的。但如果 XA 數值不穩定同時 XAB 數值穩定的話,那么有兩種情況:XA 數值偏大、B 數值偏小,根據求導公式,這將導致 A 的梯度偏小、B 的梯度偏大;反過來,XA 數值偏小、B 數值偏大,這將導致 A 的梯度偏大、B 的梯度偏小。
總而言之,XA 的數值不穩定會導致 A,B 的梯度不穩定,從而增加優化難度,所以還是加上 XA 的數值穩定性為條件比較好。



貢獻相當

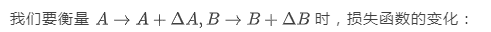
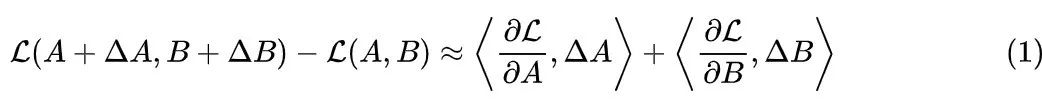
這里使用了一階線性近似,其中 是 A,B 的梯度, 是(Frobenius)內積運算,右端兩項就可以理解為 A,B 對效果的分別貢獻。但注意線性近似的有效性取決于增量 是小量,但對于訓練好的權重,它對于原始權重的增量還真未必是小量。
所以退而求其次,我們將“貢獻相當”假設改為“A,B 在每一步更新中應該對效果有同等程度上的貢獻”,由于單步更新的量通常很小,因此線性近似能比較好地滿足。
既然要考慮每一步的更新量,那么就引導我們到了優化器的方向上。當前預訓練和微調的主流優化器都是 Adam,那么我們就以 Adam 為主要分析對象。

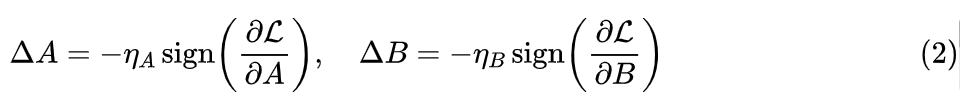
其中 是各自的學習率,“LoRA+”的結論就是 。
將 SignSGD 的增量(2)代回式(1),那么就得到



快速推導
進一步的分析需要求出梯度的具體形式。再次設 Y=XAB,那么可以求出:
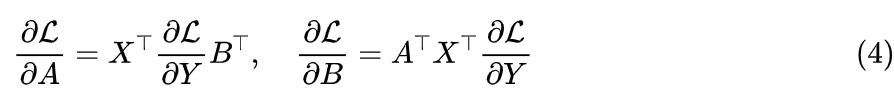



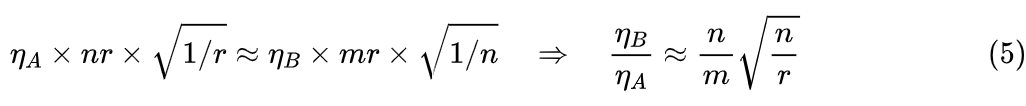


但是還沒完,我們要檢查一下結果是否自洽,因為我們用到的條件之一是“前向的數值穩定性”,至今為止還只是一個理想的假設。如何讓假設盡可能成立呢?戰勝一個假設的方法是引入另一個假設:

根據 Adam 的近似式(2),每步增量的數量級確實正比于學習率,但總的更新結果又不完全是每一步簡單疊加,所以這個假設給人的感覺就是“看上去有點道理,但又不完全有道理”。但不要緊,假設通常都是這樣子的,有點道理就行,剩下的就只能靠信仰了。


文章小結
這篇文章中,我們介紹并推導了一個名為“LoRA+”的結果,它支持 LoRA 的兩個低秩矩陣 A,B 存在固有的不對稱性,不管將哪個矩陣全零初始化,都應該將 B 的學習率設置得大于 A,以達到更優的效果。
本文轉載自 ??PaperWeekly??,作者: 蘇劍林


















