本文將講述一個高效的不重復隨機數(shù)列的生成算法，其效率比通常用hashtable 消重的方法要快很多。

首先我們來看命題：

給定一個正整數(shù)n，需要輸出一個長度為n的數(shù)組，數(shù)組元素是隨機數(shù)，范圍為0 – n-1，且元素不能重復。比如 n = 3 時，需要獲取一個長度為3的數(shù)組，元素范圍為0-2，

比如 0,2,1。

這個問題的通常解決方案就是設(shè)計一個 hashtable ，然后循環(huán)獲取隨機數(shù)，再到 hashtable 中找，如果hashtable 中沒有這個數(shù)，則輸出。下面給出這種算法的代碼

public static int[] GetRandomSequence0(int total)  
{  
    int[] hashtable = new int[total];  
    int[] output = new int[total];  
 
    Random random = new Random();  
    for (int i = 0; i < total; i++)  
    {  
        int num = random.Next(0, total);  
        while (hashtable[num] > 0)  
        {  
            num = random.Next(0, total);  
        }  
 
        output[i] = num;  
        hashtable[num] = 1;  
    }  
 
    return output;  
} 

代碼很簡單，從 0 到 total - 1 循環(huán)獲取隨機數(shù)，再去hashtable 中嘗試匹配，如果這個數(shù)在hashtable中不存在，則輸出，并把這個數(shù)在hashtable 中置1，否則循環(huán)嘗試獲取隨機數(shù)，直到找到一個不在hashtable 中的數(shù)為止。這個算法的問題在于需要不斷嘗試獲取隨機數(shù)，在hashtable 接近滿時，這個嘗試失敗的概率會越來越高。

那么有沒有什么算法，不需要這樣反復嘗試嗎？答案是肯定的。

 如上圖所示，我們設(shè)計一個順序的數(shù)組，假設(shè)n = 4

***輪，我們?nèi)?0 – 3 之間的隨機數(shù)，假設(shè)為2，這時，我們把數(shù)組位置為2的數(shù)取出來輸出，并把這個數(shù)從數(shù)組中刪除，這時這個數(shù)組變成了

第二輪，我們再取 0-2 之間的隨機數(shù)，假設(shè)為1，并把這個位置的數(shù)輸出，同時把這個數(shù)從數(shù)組刪除，以此類推，直到這個數(shù)組的長度為0。這時我們就可以得到一個隨機的不重復的序列。

這個算法的好處是不需要用一個hashtable 來存儲已獲取的數(shù)字，不需要反復嘗試。算法代碼如下：

public static int[] GetRandomSequence1(int total)  
{  
    List<int> input = new List<int>();  
    for (int i = 0; i < total; i++)  
    {  
        input.Add(i);  
    }  
 
    List<int> output = new List<int>();  
 
    Random random = new Random();  
    int end = total;  
    for (int i = 0; i < total; i++)  
    {  
        int num = random.Next(0, end);  
        output.Add(input[num]);  
        input.RemoveAt(num);  
        end--;  
    }  
 
    return output.ToArray();  
}  

這個算法把兩個循環(huán)改成了一個循環(huán)，算法復雜度大大降低了，按說速度應該比***個算法要快才對，然而現(xiàn)實往往超出我們的想象，當total = 100000 時，測試下來，***個算法用時 44ms, 第二個用時 1038 ms ，慢了很多！這是為什么呢？問題的關(guān)鍵就在這個 input.RemoveAt 上了，我們知道如果要刪除一個數(shù)組元素，我們需要把這個數(shù)組元素后面的所有元素都向前移動1，這個移動操作是非常耗時的，這個算法慢就慢在這里。到這里，可能有人要說了，那我們不用數(shù)組，用鏈表，那刪除不就很快了嗎？沒錯，鏈表是能解決刪除元素的效率問題，但查找的速度又大大降低了，無法像數(shù)組那樣根據(jù)數(shù)組元素下標直接定位到元素。所以用鏈表也是不行的。到這里似乎我們已經(jīng)走到了死胡同，難道我們只能用hashtable  反復嘗試來做嗎？在看下面內(nèi)容之前，請各位讀者先思考5分鐘。

#p#

…… 思考5分鐘

[[20734]] 

#p#

算法就像一層窗戶紙，隔著窗戶紙，你永遠無法知道里面是什么，一旦捅穿，又覺得非常簡單。

還是上面那個例子，假設(shè) n = 4

***輪，我們隨機獲得2時，我們不將 2 從數(shù)組中移除，而是將數(shù)組的***一個元素移動到2的位置

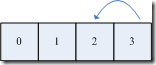
 這時數(shù)組變成了

 第二輪我們對 0-2 取隨機數(shù)，這時數(shù)組可用的***一個元素位置已經(jīng)變成了2，而不是3。假設(shè)這時取到隨機數(shù)為1

我們再把下標為2 的元素移動到下標1，這時數(shù)組變成了

以此類推，直到取出n個元素為止。

這個算法的優(yōu)點是不需要用一個hashtable 來存儲已獲取的數(shù)字，不需要反復嘗試，也不用像上一個算法那樣刪除數(shù)組元素，要做的只是每次把數(shù)組有效位置的***一個元素移動到當前位置就可以了，這樣算法的復雜度就降低為 O(n) ，速度大大提高。

經(jīng)測試，在 n= 100000 時，這個算法的用時僅為7ms。

下面給出這個算法的實現(xiàn)代碼

/// <summary>  
/// Designed by eaglet  
/// </summary>  
/// <param name="total"></param>  
/// <returns></returns>  
public static int[] GetRandomSequence2(int total)  
{  
 
    int[] sequence = new int[total];  
    int[] output = new int[total];  
 
    for (int i = 0; i < total; i++)  
    {  
        sequence[i] = i;  
    }  
 
    Random random = new Random();  
 
    int end = total - 1;  
 
    for (int i = 0; i < total; i++)  
    {  
        int num = random.Next(0, end + 1);  
        output[i] = sequence[num];  
        sequence[num] = sequence[end];  
        end--;  
    }  
 
    return output;  
}  

原文鏈接： http://www.cnblogs.com/eaglet/archive/2011/01/17/1937083.html

【編輯推薦】

1. 為自己做一個簡單記賬簿
2. 一步一步設(shè)計你的數(shù)據(jù)庫1
3. 數(shù)據(jù)庫入門級之算法【一】
4. 數(shù)據(jù)庫入門級之算法【二】
5. 數(shù)據(jù)庫入門級之算法【三】