羅馬12毫米骰子，PAS(一個英國政府管理下的保護文物志愿者組織)/大英博物館董事(CC BY-SA 2.0)

統計學家弗朗西斯 · 加爾頓于1890 年《自然》雜志上寫道：“作為一個選擇隨機的工具，我發現沒有什么優于骰子。把它們扔進裝骰子的盒子中搖動，它們彼此相互沖撞，并與盒壁碰彈，不停的滾動，即使在一次搖骰子中，骰子的最初朝向也無法為其最終的朝向提供任何有用的線索。”

我們如何才能生成一個均勻的隨機數序列?大自然中產生的如此美麗和豐富的隨機性并不總可以被輕松的提取和量化。最古老的骰子是在公元前24世紀中東的一個墳墓中被發現的。大約在公元前1100年，在中國，龜卜中火熱龜殼直到其隨機破裂，然后占卜者對龜殼裂縫進行解釋。幾個世紀之后，易經卜卦中將49條蓍草莖放在桌子上，按一定規則切分幾次，其結果類似于執行硬幣投擲。

摘自《A Million Random Digits with 100,000 Normal Deviates》

但是到了二十世紀40年代中期，現代世界需要更多的隨機數，遠超過骰子和蓍草莖可提供的范圍。蘭德公司研發了一種機器可以使用隨機脈沖發生器產生隨機數。他們運行了一段時間，并收集到一本書中《A Million Random Digits with 100,000 Normal Deviates》。現在看來，這似乎是一個好笑的藝術項目，但在當時卻是一大突破，這是第一次為公眾提供了一個高質量的長隨機數序列。蘭德公司在2001重印了該書，現在在亞馬遜上可以購買。

另外還有一個類似的機器：搖獎機，是有當時著名的Bletchley Park WWII 破譯小組于上世紀40年代設計的，用來為英國的保險債券彩票產生隨機數。為了減輕對ERNIE公正性和準確性的擔憂，公司做了一個偉大的紀錄片，稱為“E.R.N.I.E.的重要性”，非常值得一看：The Importance of Being E.R.N.I.E. 。

1951年，隨機數生成終于被正式地內嵌到一臺真正的計算機中：Ferranti Mark 1 ,它帶有一個內置的隨機數指令，可以使用電氣噪聲一次生產20個隨機比特。這個功能由阿蘭·圖靈設計，Christopher Strachey 通過利用它編寫一個隨機的情書發生器。下面是一個情書的例子，來自David Link該項目的2009 復合計劃。

但是圖靈的隨機數字指令讓當時的程序員感到非常困惑,因為它在一個已經如此不可預測的環境中造成了太多的不確定性。人們期望軟件的一致性，但使用該指令的程序永遠無法以一種一致性的可重復方式運行，這使得測試幾乎不可能。

如果一個隨機數發生器可以表示為確定性函數呢?如果可以重復調用一個隨機數序列，但在相同的初始化條件下，它總是會產生相同的序列呢?這就是偽隨機數發生器(PRNG)。

馮·諾依曼在1946年左右開發了一個PRNG，他的想法是從一個初始的隨機種子值開始對其平方，然后截取平方結果的中間若干位，得到一個新的數字，接下來重復對得到的數取平方并截取中間若干位的過程，就會得到一個具有統計意義屬性的隨機數序列了，這也就是廣為人知的平方取中法。

馮·諾依曼的方法沒有經受住時間的考驗，因為無論使用什么樣的種子值，序列最終會陷入一系列短重復周期的數字，如8100，6100，4100，8100，6100，4100……

當使用確定性函數生成隨機數序列時，如果后續值基于先前值，避免循環是不可能的。但是如果周期足夠長，使之對隨機序列實際上影響不大呢?

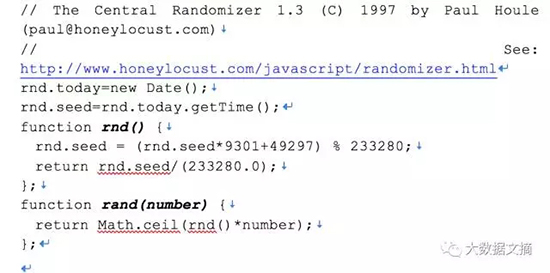
依照這一想法，數學家D.H.Lehmer在1949年提出了線性同余生成器(LCG)。這里介紹一個簡單的PRNG，叫做中央隨機數生成器，便是基于Lehmer的方法，于1995年采用JavaScript編寫實現如下：

注意這里的所有幻數，選擇這些數字(通常是素數)用來最大化周期：在rand()生成序列之前迭代次數將自我重復。該PRNG使用當前時間作為種子值，其周期值約為2的31次方。

中央隨機生成器指針變得流行是因為JavaScript 1.0沒有內置的Math.random()函數，每個人都希望他們的Web 1.0橫幅廣告隨機旋轉。開發者Paul Houle寫道：“我不會用它來保密，但它對許多用途都是有好處的。”

然而互聯網確實需要保密。 SSL誕生于1995年左右，其加密方案要求高質量的PRNG，這種發展可能導致了一段RNGs 迅猛創新的時期。如果查看所有的隨機數生成器的專利，可能會感覺就像現代版的第一次制造飛機的浪潮一樣。

20世紀90年代中期最常見的CPU沒有生產隨機數的指令，所以好的隨機種子很難在當時得到。當Phillip Hallam-Baker發現Netscape的SSL網絡服務器(當時市場上最大的一個)使用當前時間和幾個進程ID的組合作為其隨機數生成器的種子時，才意識這將成為一個真正的安全問題。哈拉姆·貝克(Hallam-Baker)表示，攻擊者可以很容易地猜到種子值，并采用各種手段解密服務器的流量。 猜測種子值是一種常見的攻擊，盡管它已經變得越來越復雜了。這是 2009年在 Hacker News 上的一段非常經典的攻擊演練。

到1997年，計算機科學家們對生成隨機數的有限選項感到厭倦，所以SGI的一個團隊創建了LavaRand，這是一個網絡攝像頭，指向桌面上的幾個熔巖燈。相機的圖像數據是一個很好的熵源：就像圖靈的真正隨機數生成器(TRNG)，并且它可以以165Kb / s的速率生成隨機數據。在當時的硅谷時代，熔巖燈平臺迅速獲得專利。

Autodesk的創始人約翰·沃克(John Walker)意圖在世界各地推廣他的 HotBits，一個隨機數字生成服務應用程序，由一個保證真正量子隨機性的蓋革計數器支持。 Random.org創建于1998，為互聯網提供免費的隨機數，他們現在提供的手機應用程序可以實現真正的隨機拋硬幣，扔骰子，撲克洗牌等。

大多數的這些發明都半途而廢，但是一個叫做梅森旋轉隨機數生成器(The Mersenne Twister)的PRNG 軟件被推廣，在1997 由松本眞和西村拓士發明。它完美地平衡了性能和隨機數的質量，并且經受住了時間的考驗。它基于線性反饋移位寄存器(LFSR)的思想，產生一個循環周期非常長的確定性序列。近期的應用中，其循環周期可達到 2¹⁹⁹³⁷− 1。在如今的編程語言中，這種算法依舊是默認的 PRNG。

終于在1999發生了一個很大的轉變。英特爾在其i810芯片組中增加了一個內置的隨機數發生器。這使得新的服務器具備了來自熱噪聲的本地源隨機數生成能力——真正的隨機數生成器(TRNG)。這非常具有進步意義，但速度仍不如軟件PRNGs快，所以加密軟件仍然不得不依靠一個偽隨機數發生器。

這節我們介紹安全加密的PRNG(CSPRNG)，(這些縮寫!難怪有些人認為計算機科學是枯燥的。)在SSL的時代CSPRNG非常重要。什么是CSPRNG?這里有一份 131 頁的論文來介紹 CSPRNG，希望你能愉快閱讀。

不言而喻，CSPRNG 具有很強的要求。梅森旋轉隨機數生成器并不是一種 CSPRNG，因為如果可以給定大量的先前序列樣本，后面的數字可以預計出來。最近，2012年英特爾在真隨機數發生器上增加了 RDRAND 和RDSEED指令，采用片上熱噪聲發生器可提供500MB/s的吞吐量。但RDRAND 的完整性一直被質疑。是不是存在細小的缺陷?或者是為國家安全局內置了什么東西?沒有人知道這個問題的答案。我猜某些地方的某些人一定知道，可是他們也一定不會公開。

采用硬件隨機數生成器 PEDOUBLER 生成的隨機數。

開源硬件TRNGs于最近些年出現，其優點源自于設計的透明化：你可以檢查電路本身，也可以在家里使用現成的組件建立它們。完全透明的設計不會讓人懷疑這些電路優秀的隨機性。REDOUBLER和無限噪聲 TRNG是兩個開源硬件隨機數生成器，鏈接中給出他們的 Github 源碼地址。

今天，關于隨機數生產方法選擇的爭論仍存在于在操作系統內核，編程語言，和安全包(如 OpenSSL 或者 OpenSSH)等方面。這些算法存在多種變形用以滿足不同的速度、空間和安全要求，安全專家總是在尋找新的方法來攻破已有算法的實現。但是對于日常使用，在大多數的操作系統中我們可以放心地使用 /dev/random，或者編程語言中的 rand() 函數，它們都可以快速得到一段足夠長的隨機數列，并且你這么做，阿蘭·圖靈也會很開心。

來源：https://medium.freecodecamp.com/a-brief-history-of-random-numbers-9498737f5b6c

【本文是51CTO專欄機構大數據文摘的原創譯文，微信公眾號“大數據文摘（ id: BigDataDigest）”】

戳這里，看該作者更多好文