三、對于效率提高的初次嘗試

      對于最自然的幾種排序算法，數學家們開始思考如何提高排序算法的效率，可以通過數學證明出來如果想達到這個目的，必須想辦法將相距較遠的元素進行交換，具體原理涉及到比較一定的數學證明，因為我不是學數學出生的，所以我不能完整嚴謹的寫出這個證明，所以，套用一句俗話吧，如果感興趣你可以自己查閱一下資料。

      希爾排序是以其發明人Shell的名字命名的。這里有個故事就是在一些書上，這個算法被稱作是Shell-Metzner排序法，但是呢，這個叫做Metzner的人說“我沒有為這種算法做任何事，我的名字不應該出現在算法的名字中。”有沒有瞬間覺得這個Metzner實在是太偉大了？特別是在現在這個大環境下，這種人如果能多出現在高等教育上，頓時覺得中國的高等教育有希望了。作為***批沖刺突破二次時間界的算法之一，從交換距離較遠的元素這個思路出發，在每一次的交換中獎待排序數列分為若干對，兩兩交換，但是這兩個對的距離由近及遠，不停地交換，看起來感覺有點抽象，那么就先從代碼開始好了。

void ShellSort(int numbers[],int array_size) 
{ 
    int j=0; 
    for(int gap=array_size/2;gap>0;gap=gap/2) 
    {   
        cout<<"Sort time number "<<(j+1)<<":"; 
        for(int i=gap;i<array_size;i++) 
        { 
          int tmp=numbers[i]; 
          int j=i; 
          for(;j>=gap&&tmp<numbers[j-gap];j-=gap) 
          { 
              numbers[j]=numbers[j-gap]; 
          } 
          numbers[j]=tmp; 
        } 
        for (int i = 0; i < array_size; i++){ 
            cout<<numbers[i]<<" "; 
        } 
        j++; 
        cout<<endl; 
    } 
 
} 

     這個代碼很值得研究，除去***的打印代碼，這個排序里面竟然用了三次循環，重要的是雖然是三次循環但是卻提高了效率!所以說，有的時候，事情不僅僅不是你看到的那樣而且換一種看似不 看起來確實令人挺不可思議的，但是為什么呢，如果讓我從一個最通俗的方式來解釋的話，雖然這里有三個循環，但是在你會發現因為外面兩個循環的原因，最里面一個循環執行的次數是很少的，另外一個原因就是這里的步長，步長不是逐個增加導致了循環次數的減少，從而使得性能的提高。

     這一段話貌似還是很讓人覺得略有些在裝B，所以，還是結合實際的數解釋一下增加點親切感。

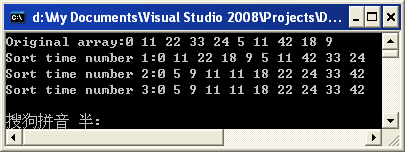
      結合代碼和結果來看，這里有十個數，最開始的步長是5，那么***輪分別比較（0,5），（11,11），（22，42），（33,18），（24，9），兩兩比較之后進行交換的結果如第二行所示，這時候最內層循環一共執行了2次，接下來，步長減半，比較的順序應該是(0,22),(11,18),[(22,9)（進行交換）和(9,0)],[(5,18）（有交換）和(5,11)（有交換）],后面我就不列舉了，實在是列舉不動了，眼睛和腦子雙雙都不行了，在你完成全部列舉完成的時候很輕松就可以看到在第三輪的時候基本上已經不需要進行交換了，這和顯示出來的是一樣的，這說明了在第三輪的時候最內層循環一次交換操作也沒有進行，而外面兩層主要是遍歷，相比于交換，它所耗費的資源要少的多，換句話說，由于前面的大步長的時候進行了一些大刀闊斧的排序，導致在后面的小步長的時候只要做些許修正就可以了，有一部分情況下是完全不需要修正的，這樣也得到了一個效率上的提高。

     所以說增量的選擇對于希爾排序能否達到提高的效果是十分重要的，這里采用的是最簡單不斷將步長減半的方式，一般來說，最簡單的效果肯定不是***的，對于希爾排序增量選擇的研究是非常多的，這個還是需要一定的數學知識的，有一種Hibbard增量可以使得希爾排序的速度達到0(N^2/3),這也是為什么希爾排序是能突破二次時間界的算法。

四、圈圈圓圓圈圈

      在提高排序算法的效率上，各個大牛數學家努力的想辦法減少比較次數，從而減少交換的速度，在此基礎上，大牛們又發明了歸并排序，快速排序的算法，使得排序的時間界達到了O(N*LOGN），而這后來也被證明了是基于交換的排序算法的時間下界。也就是說，只要你的思想離不開比較交換，排序算法的最快也就這么快了。

     歸并排序和快速排序的寫法相對于前面的提到的要看起來“高帥富”很多，看起來非常復雜的原理用幾行就寫完了，而且邏輯很清晰，這一切都是得益于實現它們的時候通常都采用了遞歸的結構，這就像“高帥富”的跑車，先別管這個“高帥富”是否真的帥，開一個跑車出來讓你看看至少已經讓你在心中有了幾分對于“高帥富”的敬畏，至于從車上出來的人到底是怎樣的人，與他的車帥不帥關系不大。這就像用遞歸結構實現的算法，使用遞歸結構往往會使人覺得這個算法看起來很牛逼，而且可以使這個算法思想看起來十分清晰，但是至于這樣實現效率是否高效，那就不一定了。

     在寫這兩個算法之前，首先非常有必要闡述一下遞歸的思想，說到遞歸，簡單的用程序的語言來解釋就是不定的調用自己直到滿足某一個條件結束輸出某一個值或者進行某一個操作，很多人***個想到的應該是斐波那契數列，其實吧，我覺得很多書把這個作為遞歸思想的啟蒙例子很有誤導性，因為斐波那契數列的計算，如果使用遞歸的話，效率是非常差的，雖然這個求斐波那契數列某一項的代碼很簡單，我還是貼出來一下。

int Fibonacci(int n) 
{ 
    if(n==0||n==1) 
        return n; 
    else 
        return Fibonacci(n-1)+ Fibonacci(n-2); 
} 

     我們來測試一下它的運行時間好了，我們求前50項的值，看看它所要耗費的時間。

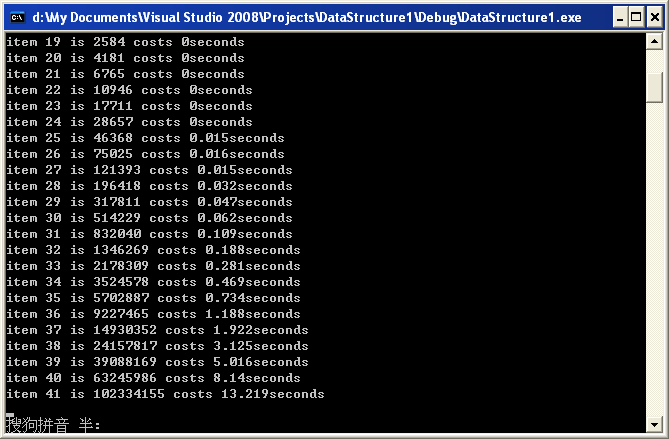
     我已經等不到第50項的值出來了，從運行結果可以看到到第39項的時候運行時間已經開始飆升了，到不了第50項就已經到了無法忍受的地步了，這明顯完全無法滿足實際的要求，某種程度上這會給人一種誤導，遞歸在實際運用中用處不大。明顯，這種想法是錯誤的。

     來看這樣一個例子，將一個數字倒序輸出，比如輸入的是12345，輸出是54321，這個問題的解法相當簡單，就是不停將自身的對10取余，不停地數以10。這個解法符合遞歸的思想，其代碼如下所示：

void PrintReverse(int n) 
{ 
    if(n!=0) 
    { 
        cout<<n%10; 
        PrintReverse(n/10); 
     
    }     
} 

     這樣的一個例子就適合用遞歸的思想去做，因為一個整數很少能大到擁有100位以上，所以這個遞歸算法的運行效率會很高，加上這個程序從上到下讀下來和我前面說的基本思想非常的符合，比較符合人的邏輯思維習慣，增加了程序的可讀性。所以說，遞歸并不是像有些書里面說的那樣，效率低，一般情況下盡量不要用，任何一樣東西都沒有絕對的好壞，只有你有沒有用到適合的地方。

      ***，一個經常遇到的問題是不是任何遞歸都能轉換成為非遞歸的程序呢？答案是可以的，只要你運用適當的數據結構，都能轉換成為非遞歸程序，但是轉換的過程并沒有那么的簡單，所以將遞歸轉換成為非遞歸，有時候還是需要一定的數學知識的。