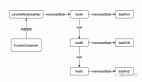
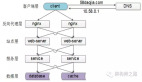
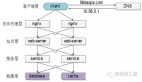
關(guān)于SLG游戲引入蘭切斯特方程的設(shè)想
蘭切斯特方程一直是大型沙盤戰(zhàn)場推演所用,能較為準(zhǔn)確的推算出戰(zhàn)爭傷亡,損失。可以想象一下,將這個用在戰(zhàn)略游戲,讓戰(zhàn)略游戲不再是簡單的屬性沖撞,會不會帶來更加真實(shí)直觀的感受~
一、介紹蘭切斯特方程(摘自維基百科,百度百科)
1914年英國工程師蘭切斯特(F.W.Lanchester)在研究空戰(zhàn)單位最佳編制的“戰(zhàn)斗中的飛機(jī)”一文中率先提出了其著名的蘭切斯特方程。
開始是用于分析交戰(zhàn)過程中的雙方傷亡比率,后用途逐漸推廣。
蘭切斯特把戰(zhàn)斗簡化為兩種基本情況:遠(yuǎn)距離交火和近距離集中火力殺傷。遠(yuǎn)距離交火時,一方損失率既和對方兵力成正比,也和己方兵力成正比,以微分方程表示即為:
dy/dt=-a*x*y
dx/dt=-b*x*y
其中x和y分別為紅軍和藍(lán)軍的戰(zhàn)斗單位數(shù)量,a和b分別為紅軍和藍(lán)軍的平均單位戰(zhàn)斗力,因此雙方實(shí)力相等的條件為:
a*x=b*y
二、簡單總結(jié)
近距離交戰(zhàn)時,任何一方參戰(zhàn)單位數(shù)量與參戰(zhàn)單位戰(zhàn)斗效率成正比,概稱之為蘭切斯特線性定律;
(對于古代戰(zhàn)爭,拿長矛的重步兵方陣,其中一個士兵只能同時攻擊到另一個士兵。每個士兵只能要么干掉對面的,要么被對面的干掉,那么戰(zhàn)后損失將是兩支部隊之間的數(shù)量差,在武器(戰(zhàn)斗力)無差異的情況下。)
遠(yuǎn)距離交戰(zhàn)時,任何一方參戰(zhàn)單位數(shù)量與參戰(zhàn)單位戰(zhàn)斗效率的平方成正比,概稱之為蘭切斯特平方定律。
(對于射擊性武器在遠(yuǎn)距離瞄準(zhǔn)射擊的情況下,他們可以射擊敵方陣線中的任何敵人,也會被地方陣線中的任何敵人攻擊到。這時軍隊消耗得比率將之于雙方的火力數(shù)量有關(guān)(假設(shè)無戰(zhàn)斗力差異)。蘭切斯特認(rèn)為這樣的軍隊的實(shí)力不只與軍隊的數(shù)量,而是與數(shù)量的平方有關(guān)。)
在雙方戰(zhàn)斗力可以量化的情況下,強(qiáng)大的一方每增長一點(diǎn),優(yōu)勢是以幾何遞增。
簡單舉個例題說明吧:
2000輛德軍坦克圍攻1000輛蘇軍坦克,假設(shè)雙方坦克的性能一模一樣,雙方都沒有指揮官,問:德軍將損失多少輛坦克才能全殲蘇軍坦?
答案是損失268。
計算方式如下:
sqrt(a*X^2-b*Y^2)=sqrt(2000^2-1000^2)=1732
2000-1732=267.9=268
三、關(guān)于帶入SLG游戲的應(yīng)用設(shè)想
跟朋友討論某當(dāng)紅slg手游,由于沒有戰(zhàn)斗表現(xiàn),依舊玩的樂此不疲,所以數(shù)值尤為重要,覺得有些東西可以拉出來談?wù)劊P(guān)于此方程與游戲的關(guān)系,并且能給游戲帶來什么樣不同的感受,還有就是方程的擴(kuò)展性。
首先建立一個簡單的模型吧。
規(guī)則
-
克制系數(shù)關(guān)系
-
弓克騎
-
騎克步
-
步克弓
-
隨手拍的,克制系數(shù)為1.2
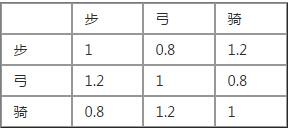
此系數(shù)直接用來量化方程的其他不穩(wěn)定因素,例如,射程,移動速度,士兵氣血差距,攻擊速度等,兵力消耗或者補(bǔ)給消耗都默認(rèn)為自然損耗狀態(tài)。(克制系數(shù)可等價抵消:1步兵=0.8弓兵=1.2騎兵)
結(jié)合以上條件,可以確定一個思路,將模型盡量統(tǒng)一化,用克制系數(shù)來然后用方程去計算戰(zhàn)斗結(jié)果,由于是游戲并非實(shí)戰(zhàn),我們可以很主觀的定義,游戲中每個單位,在每場戰(zhàn)斗中,至始至終都能發(fā)揮出本身能發(fā)揮的作用,所以此處用平方率,不涉及線性定律。
首先最簡單的:
步兵 10 VS 步兵 10
在統(tǒng)一前提條件下,毫無疑問會是勢均力敵。
下面來為一方增加一點(diǎn)優(yōu)勢:
步兵 10 VS 步兵 11
sqrt(11^2-10^2)=4
增加1個的兵力,就能多保住三個步兵。
弓兵 3000 VS 步兵 1500
sqrt(a*X^2-b*Y^2)=sqrt(3000^2-0.8*1500^2)=2683
為了更加易懂,a代表弓兵質(zhì)量,x代表弓兵數(shù)量,b代表步兵質(zhì)量,y代表步兵數(shù)量。
3000-2683=317
接著,可以看看復(fù)雜一點(diǎn)的部隊?wèi)?zhàn)斗。
混戰(zhàn)如果嚴(yán)謹(jǐn)?shù)氖褂锰m切斯特方程,式子大概是這樣:
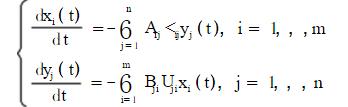
但是游戲歸游戲,公式再復(fù)雜,帶來的體驗不一定會很好。這里面Xi(t)為X方i類的作戰(zhàn)兵力,Aij為y方第j類武器對x方第i類目標(biāo)的損傷系數(shù),下面可以類推,接著就是分配矩陣系數(shù)(不寫了,免得有人噴我,有興趣的可以接著推算下去~)
單純用模型轉(zhuǎn)換可以更加簡單的推算出結(jié)果:
首先,定義為雙方兵力占比最大的兵種為初始模型;
損失兵種按照損失兵力與原有兵力最大比例分配。
(此處可以再復(fù)雜一些,例如,步兵傷亡小于百分之30,弓兵不損失,或者有騎兵情況下,步兵傷亡百分之20,則會開始損失弓兵等設(shè)定,以帶來更加真實(shí)的體驗為目的)
A方 弓兵 1000 步兵 1500 VS B方 弓兵 2000 步兵 1000
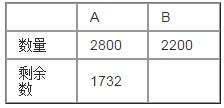
函數(shù)=sqrt(a*X^2-b*Y^2)=1732
B弓兵剩余1237
B步兵剩余495
到了這里,大概計算應(yīng)該都沒有什么問題了,現(xiàn)在,我們可以加入游戲通用的養(yǎng)成元素,SLG常用的,例如,士氣,主角屬性帶入,天氣影響,地勢系數(shù)等等,可見基于此計算方式上面的游戲,擴(kuò)展性不比數(shù)值碰撞,公式加減乘除來的少。
題外話~
做這個之前,網(wǎng)上看到有人測試,魔獸爭霸里面,在不干涉情況下,10個步兵打10個人族步兵,11個打10個,12個打十個~結(jié)果與蘭切斯特方程計算出來的結(jié)果幾乎一樣。雖然魔獸爭霸注重操作,一個老手能很輕松的將消耗降到最低,但是在大型戰(zhàn)役中,雙方如果勢均力敵,結(jié)果最后毫無疑問將會與參戰(zhàn)人數(shù),質(zhì)量等數(shù)據(jù)掛鉤,此時方程將會發(fā)揮出巨大的作用,可以推演出戰(zhàn)損以及耗費(fèi)資源等,以此來布局排布,在slg游戲中,如果忽略其戰(zhàn)斗表現(xiàn),最終結(jié)果將給玩家更加真實(shí)的感受。