運行大規(guī)模網(wǎng)絡(luò)服務(wù)(例如內(nèi)容托管)離不開負載平衡，也就是將客戶端均勻地分配到多個服務(wù)器上，使得每個服務(wù)器都不至于過載。此外，在隨時可以添加或移除客戶端和服務(wù)器的動態(tài)環(huán)境中，較為理想的做法是找到一種不會隨時間而大幅改變的分配方案。換而言之，我們需要在一段時間內(nèi)一致地將客戶端分配到服務(wù)器。

背景

盡管過去已經(jīng)研發(fā)出一致的哈希算法理念來解決動態(tài)環(huán)境中的負載平衡問題，但所有之前開發(fā)的方案都存在一個根本性的問題：在特定的場景下，它們可能導(dǎo)致許多服務(wù)器上的負載平衡不能達到***狀態(tài)。

此外，由于可能隨時添加或移除客戶端和服務(wù)器，在做出此類改動時，我們不希望移動太多的客戶端。因此，動態(tài)分配算法不僅必須始終確保正確的負載平衡，還應(yīng)盡量減少每次對系統(tǒng)做出改動之后所移動的客戶端數(shù)量。當(dāng)每臺服務(wù)器的容量存在嚴格的限制時，也就是說，每臺服務(wù)器都有嚴格的容量限制，負載不得超過此限制之時，此類分配問題會變得更為嚴峻。通常，我們希望容量接近于平均負載。

換而言之，我們希望在最終的分配中同時實現(xiàn)均勻性和一致性這兩大目標。對于服務(wù)器集固定不變、只有客戶端集會更新這種簡單很多的情形，有大量的文獻介紹了相關(guān)的解決方案，但在本文中，我們討論的解決方案針對的是客戶端和服務(wù)器均可隨時添加和移除的完全動態(tài)的情形。

算法

我們可以將服務(wù)器比作垃圾桶，將客戶端比作球，并借鑒將球隨機投入垃圾桶的過程 (balls-to-bins stochastic processes) 這一經(jīng)過深入研究的模型，采用與之類似的抽象方法。均勻性目標要求所有垃圾桶所裝的球數(shù)量大致等于平均密度(球數(shù)除以箱子數(shù))。對于參數(shù) ε，我們將每個垃圾桶的容量設(shè)置為平均負載的***或***倍數(shù) (1+ε)。這一額外的容量讓我們可以設(shè)計出一種能夠同時滿足均勻性目標和一致性目標的分配算法。

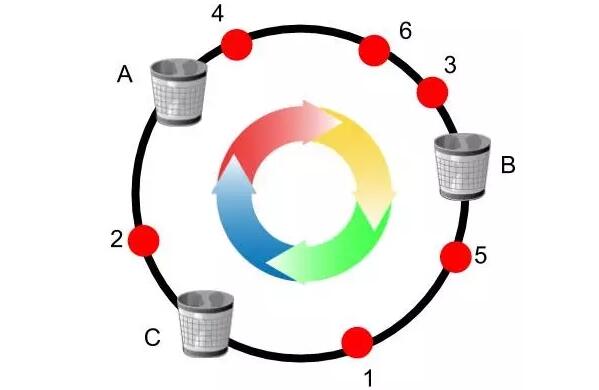
設(shè)想給定范圍的一組數(shù)字，將其分布到一個圓圈上。我們對球應(yīng)用一個哈希函數(shù)，對垃圾桶應(yīng)用另一個不同的哈希函數(shù)，以獲取該范圍內(nèi)、與該圓圈上不同位置對應(yīng)的數(shù)字。隨后，我們開始按特定的順序分配球，此順序與其哈希值無關(guān)(假設(shè)基于其 ID)。然后，按順時針移動每個球并將其分配到***個有空閑容量的垃圾桶。

我們分析一下上面的例子，我們使用兩種不同的哈希函數(shù)，將 6 個球和 3 個垃圾桶隨機分配到圓圈上的不同位置。對于本例，我們假設(shè)每個垃圾桶的容量設(shè)置為 2。我們開始按 ID 值的升序分配球。1 號球按順時針移動，進入垃圾桶 C。2 號球進入垃圾桶 A。3 號和 4 號球進入垃圾桶 B。5 號球進入垃圾桶 C。6 號球順時針移動，首先***垃圾桶 B。然而，垃圾桶 B 的容量為 2，而其中已經(jīng)裝有 3 號和 4 號球。因此，6 號球繼續(xù)向前移動，直至到達垃圾桶 C，但該垃圾桶也已滿。***，6 號球進入仍有空余位置的垃圾桶 A。

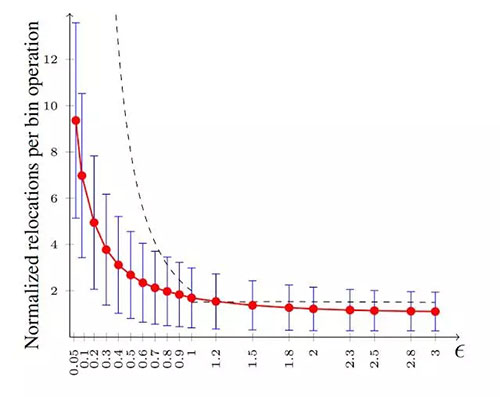
如對系統(tǒng)進行任何更新(插入/刪除球或垃圾桶)，則會重新計算分配，以保持均勻性目標。分析表明小幅更新(插入和刪除少量的球或垃圾桶)會導(dǎo)致分配狀態(tài)的小幅改變，因此，可滿足一致性目標。在我們的論文中，我們展示了在該系統(tǒng)中，每插入或移除一個球?qū)?dǎo)致其他球進行 O(1/ε2) 次運動。最重要的是，此上限與系統(tǒng)中球或垃圾桶的總數(shù)無關(guān)。因此，如果球或垃圾桶的數(shù)量加倍，此上限不會改變。上限與球或垃圾桶的數(shù)量無關(guān)，為可伸縮性帶來了巨大的空間，因為我們將其搬到更大的實例中，仍然可以滿足一致性目標。下面顯示了更新某個垃圾桶/服務(wù)器時，每次更新所導(dǎo)致的移動(重新分配)次數(shù)模擬結(jié)果。

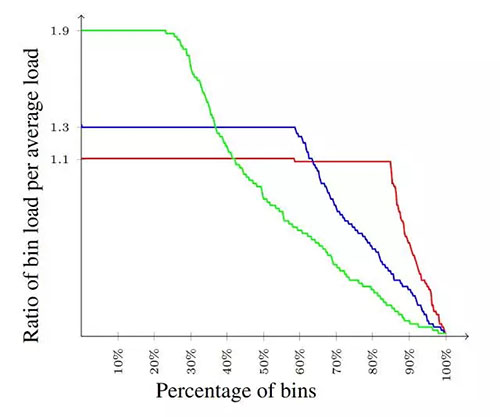
紅色曲線代表移動的平均次數(shù)，藍色柱線代表不同 ε 值(X 軸)的方差。虛線代表我們的理論結(jié)果所建議的上限，其非常適合用于預(yù)測實際的移動次數(shù)。此外，對于任何 ε 值，我們知道，每個垃圾桶的負載至多是平均負載的 (1+ε) 倍。下面，我們看到不同值 ε=0.1、ε=0.3 和 ε=0.9 條件下垃圾桶的負載分布情況。

▲ 不同 ε 值下的負載分布。對于所有范圍的負載(從 0 到 (1+ε) 倍于平均負載)，負載分布均接近均勻，許多垃圾桶的負載等于平均負載的 (1+ε) 倍。

我們可以看到，這里需要折中考慮，較低的 ε 值有利于確保均勻性，但不利于確保一致性，而較大的 ε 值則有利于確保一致性。較低的 ε 值可確保許多負載等于平均負載的 (1+ε) 倍這一硬性容量限制，而其他負載則為遞減分布。

在提供內(nèi)容托管服務(wù)時，必須做好應(yīng)對許多不同特性的實例的準備。這種一致的哈希方案非常適合此類情形，因為即便是最糟糕的情形下，它也能有不錯的表現(xiàn)。

我們的內(nèi)部研究結(jié)果激動人心，我們更欣慰的是，更廣大的社區(qū)發(fā)現(xiàn)我們的解決方案非常有用，足以列入開放源代碼，讓任何人都可以使用該算法：

https://github.com/arodland/haproxy

【本文是51CTO專欄機構(gòu)“谷歌開發(fā)者”的原創(chuàng)稿件，轉(zhuǎn)載請聯(lián)系原作者(微信公眾號：Google_Developers)】

戳這里，看該作者更多好文